高效气波冷凝装置流动及热力学特性

于洋，刘培启，王云磊，冷闯，赵一鸣，王静娴，胡大鹏



高效气波冷凝装置流动及热力学特性

于洋，刘培启，王云磊，冷闯，赵一鸣，王静娴，胡大鹏

（大连理工大学化工机械学院，辽宁大连 116023）

利用空气动力学理论，建立高效气波冷凝波图，采用二维周期性边界模型，以理想气体为介质对高效气波冷凝分离装置流场、温度场进行数值模拟，优化气波冷凝波图，预估装置内部结构参数。建立冷凝系统热力循环模型，对其热力学特性进行分析。同时搭建实验平台，对影响系统的主要参数进行了研究。实验结果表明：利用激波增压回收高压气源压力能，可以有效恢复脱湿干气压力能。通过回收脱湿干气冷量，预冷下一循环高压进气，可以获得更低冷凝温度。该装置制冷效率存在单值最优点，高效气波冷凝实际内部膨胀效率约为63%，脱湿干气压力能最高恢复90%，且随着制冷压比增大而降低。

气波冷凝；流体动力学；数值模拟；激波；热力学过程；设计

引 言

含湿气体温度低于其露点温度时，含湿气体中的湿组分就会从气相转变为液相。利用这一原理，含湿气体冷凝分离方法被提出并被广泛应用于天然气脱水、天然气凝析液回收等领域。膨胀制冷分离可以直接利用天然气的压力能，所以在天然气处理方面具备优势。超音速旋流分离技术属于膨胀制冷分离的一种，具有工艺简单、结构紧凑和无转动部件的显著优势，近年来发展迅速，但是分离效率普遍较低，仅20%左右[1]。透平膨胀制冷与压力振荡管制冷是另外两种不同的气体膨胀制冷方法，透平膨胀制冷等熵膨胀效率很高，但是在处理含湿气体时，叶片容易发生断裂事故。尤其在天然气行业，由于注醇防冻工艺加入，天然气带液现象更为严重，透平膨胀机应用受到制约，难以稳定运行；波转子制冷是一种新型气体膨胀制冷方法[2]，该方法利用波转子通道内运动压力波实现不同流体间能量交换，无须做功叶片[3-5]，波转子制冷装置运转速度低，常见转速在3000 r·min-1以内，在抑制气液两相侵蚀以及排除设备内部积液方面具有优势。

自20世纪90年代波转子这一概念被提出后[4]，波转子技术被应用于各类增压设备上[6-11]。Hu等在传统旋转气波机工作的基础上[12]，开发了外循环耗散气波制冷机[13]，以及过膨胀气波制冷机[14]。目前制冷系统内部实际膨胀效率最高约为70%，低于透平的膨胀效率，仍具有改进空间。无论波转子应用于何领域，波转子结构特征基本相同，见图1。波转子工作特性取决于其在各种工况下的波图设计。各个喷嘴与波转子通道的开闭时间需要精确的匹配，它不仅影响波转子通道内波系非定常运动还影响冷热交界面的形态[15]。数值计算方法广泛用于波转子性能分析中[16-21]。Eidelman[22]最先开发二维计算程序，计算了转子通道渐开渐闭的影响。Larosiliere[23]建立了三维计算模型，计算高压气体入射过程，得出冷热分界面受旋转速度以及通道开闭时间影响，呈三维扭曲状。Okamoto等[24]建立三通道静止波转子压力测量平台，测得了通道壁面上静压随时间变化关系。

目前，传统气波制冷机存在热力学缺陷，即膨胀后的高压气体压力能完全损失，不能回收。过膨胀气波制冷机利用外部换热器将低温气体冷量传递给高温气体，利用激波增压提高高温气体压力能，从而恢复了系统低温排气的压力能。然而将其直接应用于天然气冷凝脱湿仍存在问题。一方面，脱湿干气压力能通过流股热量交换方式进行，需要很大的换热器，必然存在冷源损失，虽然系统压比提高了，但小压比下设备内部实际膨胀效率并没有提高，系统制冷深度有限。另一方面，从能量资源利用角度而言，制冷系统内部实际膨胀产生的冷量并没有被充分利用，而是直接损耗，造成冷源浪费。

本文旨在过膨胀气波制冷系统基础上，设计一种高效气波冷凝分离流程，利用脱湿干气冷量，在其压力能恢复之前取出冷量，预冷下次入射的高压气体，然后将温度恢复的脱湿干气再次引至高效气波冷凝装置中，利用激波增压特性直接恢复脱湿干气的压力能。一方面回收了高压气体膨胀功，恢复脱湿干气的压力能，降低了系统的压比；另一方面回收了脱湿气体的冷量，降低了高压进气温度，提高了系统制冷的深度。本文首先设计制冷波图，建立二维波转子周期计算模型，分析波转子通道内波系的运动规律，优化各个端口的空间位置，建立了各个端口理想匹配关系；其次，建立高效气波冷凝热力学模型，分析了影响系统制冷效率与深度的主要因素，为系统实验平台搭建提供依据；最后建立了高效波转子冷凝分离平台，分析了主要的结构参数与操作参数对制冷效率的影响。

1 数值方法与模型验证

1.1 数值方法

为了清晰描述波转子内部压力波的波动过程，建立了二维数值计算模型，计算波转子通道内气体非定常流动。基于模型最大计算压力小于1 MPa，最低计算温度大于258 K，模型计算方程采用理想空气作为计算介质，流动过程遵循质量守恒定律，动量守恒定律，能量守恒定律。这些控制方程可以写成如下通用形式[25]

其中为通用变量，可以代表,,,等求解变量，G、分别为广义扩散系数与广义源项。

(2)

为热传导系数，c为比热容，S、S以及S定义如下

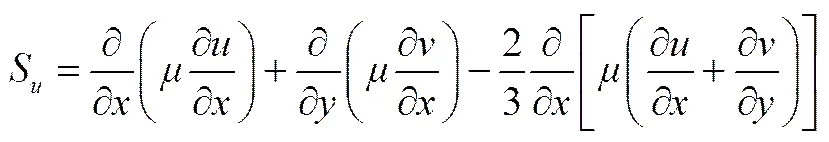
(4)

(5)

上述方程包含5个未知量，需要补充气体状态方程，使得方程组封闭。为了捕捉激波，反映激波增压特性，采用AUSM数值计算格式[26]，时间域上采用隐式积分算法。为了满足工程计算需要，采用Realizable-湍流模型[27]，Realizable-引入表征流场旋转速度参数，有效模拟平面混合流，均匀剪切流，平面射流等工况，适合本文高压喷嘴射流工况计算。

1.2 模型验证

本文依据Okamoto等[24]的三通道实验平台建立二维数值计算模型，利用了Okamoto等在双开口三管实验平台上测得的通道壁面静压随时间变化数据，验证数值模型的准确性。模型参数见表1、表2。

表1 实验结构参数

表2 实验操作参数

采用定点P10作为参考点，监测P10点壁面压力随时间变化（图2），对比Okamoto等[24]的实验结果可知，约200 μs时刻，第1道激波传至检测点P10，第1道激波增压峰值二者相差不大；约1000 μs时刻，反射激波经过检测点P10，反射激波引起增压效果二者近似。

计算表明，建立的二维模型可以很好捕捉激波的位置，且可以高精度反应激波的增压效果。图中部分精度误差主要原因为：① 计算模型采用理想气体作为计算介质；② 波转子通道壁面使用绝热边界条件，不考虑管壁导热作用；③ Realizable-湍流模型与管内实际流动存在一定误差，故计算结果仍与实际测量结果有一定偏差。但是采用该模型仍可以优化制冷波图，预估各个喷嘴与固壁尺寸，为实验设计提供参考。

2 几何模型以及数值计算结果

2.1 理想制冷波图建立

制冷波图决定波转子内部波系匹配，决定各个喷嘴空间位置关系，揭示制冷机工作机理。依据空气动力学基本理论，利用膨胀波、压缩波、激波各自特性与相互关系，合理设计制冷机内部结构，合理构建高压气体膨胀波系，获得制冷机理论极值制冷效率。本文建立波转子冷凝波系见图3。

第1道主激波S1到达高温端口(HT port)时，高温端口开启，高温端口产生反向压缩波RC1时关闭高温喷口；高压端口（HP port）闭合时产生一系列膨胀波E1，该膨胀波是冷量的主要来源，这些膨胀波在波转子通道内传至高温端口后产生反向压缩波推动波转子通道内气体从低温排气口（LT port）排出。分界面在S1、E1、RS1、E2共同作用下运动距离达到极值点。极值位置距离高压端口距离越远，高压气体膨胀越充分，膨胀制冷效率越高。

S1激波在高温端口反射产生一系列膨胀波E2，E2在波转子通道内向左传递时产生固壁反射，产生深度膨胀区E3，波转子通道内制冷区冷源由E1、E2、E3三道膨胀波系构成，由于E3膨胀波向右传递，有利于波转子内部低温气体从左侧低温出口排出。如果将E2左移至低温开口，必然会在波转子通道内产生额外的右行压缩波，右行压缩波使得波转子通道内低温气体向右端移动，不利于低温气体排气。

2.2 整机制冷模型

为了预估波转子冷凝设备内部各个喷口开启、闭合时间，建立二维数值计算模型。

波转子以母线展开，忽略高度尺度，建立二维双周期振荡管计算模型，模型见图4，图中各个参数定义见表3与表4。

波转子模型一共含有72根通道，每一个通道都是相互独立。整个模型采用四边形结构网格划分，为了清楚显示网格，取3根通道来说明，见图5。通道以固定速度向上移动，模型通道上下边界采用周期边界条件，移动通道与固定喷口采用滑移网格技术，滑移网格边界采用interface边界条件，实现数据传递。高压进口，高温出口，低压进口，低温出口均采用压力边界条件。近壁面采用标准壁面函数进行处理[21]，壁面边界网格划分为：第1层网格节点落在充分发展湍流区内。计算模型采用非稳态隐式算法，模型计算Courant数为3，固定计算时间步长为10-6s，计算稳定性较好。

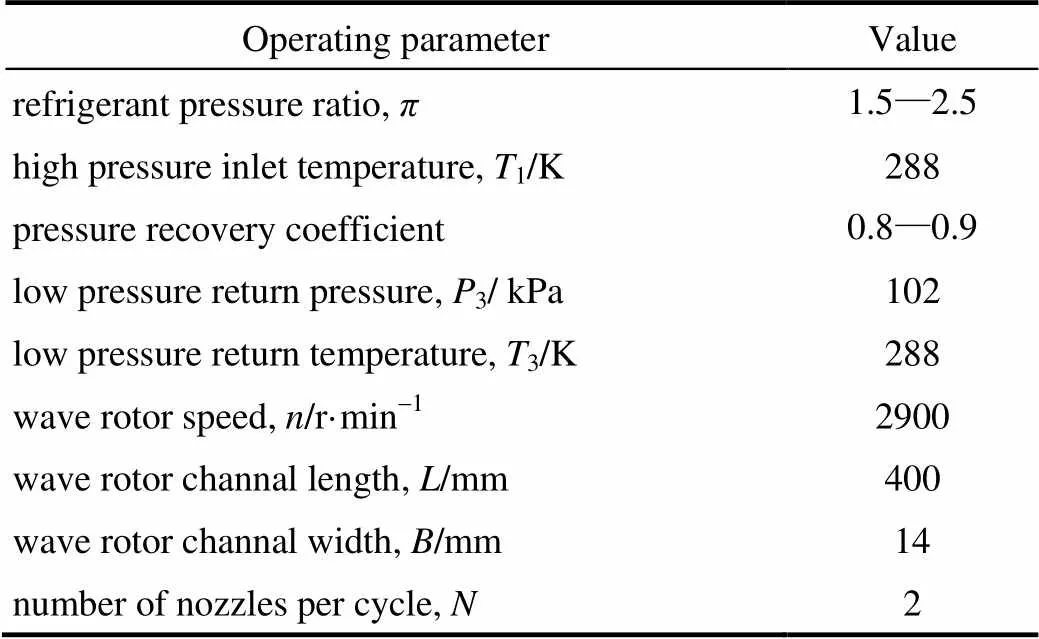
表3 计算模型边界参数

Note:14，21.

网格无关性检验见图6。任取一根通道，监测通道压力随时间变化，2 mm以上网格计算精度较差，捕捉不到低压区域因分界面扭曲引起的压力振荡现象，旋涡特征被网格尺度抹平，且当网格小于1 mm时，计算数值趋于稳定。故采用1 mm四边形结构化网格对整机模型进行网格划分。

2.3 数值计算结果

依据空气动力学波系关系，建立理想制冷波图，建立二维波转子制冷计算模型。

代入表3中边界条件，利用波图，监测低温出口温度。获得波转子冷凝装置各个端口位置与大小，获得端口特征见表4。

表4 压比1.5时实验机端口特征

图7为压比1.5时，波转子各个通道以及各个端口温度分布。低温气体在P3与P4压力差作用下排出波转子通道，低温气体排气顺利，波转子内部冷气残留较少。由于波转子通道渐开渐闭接通高温端口，故产生微量的激波反射。各个端口空间位置与大小优化比较合理。图8为优化后单个通道中线上各个节点沿管长温度随时间变化。

由图8可知，高温端口末端仍会在闭合瞬间产生一定的压缩波，会对制冷区域产生影响，但其传递至低温端口后发生开口反射，产生膨胀波再次向波转子通道右侧传递，并且逐渐衰减。

气波冷凝装置制冷区冷源主要由图3中E1、E2、E3三道膨胀波构成，-图中利用温度等值线揭示的波系与波图设计相符。计算结果为实验平台搭建提供依据。

3 热力学模型及计算结果

3.1 波转子冷凝系统热力学模型建立

本文建立高效波转子冷凝循环模型，如图9，高效波转子冷凝循环过程主要包含4个过程。① 膨胀冷凝过程：当转子通道与高压端口接通时，高压的含湿气体开始在转子通道内膨胀，温度、压力开始下降。当高压含湿气体温度降低到一定程度时，含湿组分由气相转变为液相。②分离过程：带有冷凝液的含湿气体在通道两端压差的作用下排出波转子通道，在外部分离装置中脱湿。③增压过程：脱湿后的干气被引回波转子通道，当转子通道与高压端口接通时，利用在高压含湿气体膨胀产生的激波恢复干气压力能。④低温冷量回收过程，利用换热器，将脱湿低温干气冷量换给下次入射的高压进气，从而预冷高压进气，提高制冷深度。

建立模型基于以下几点假设：① 波转子等效为同轴相连的压缩机与膨胀机组合，对外没有对外轴功输出；② 外部风机，压缩机效率都为0.75；③冷却器压降为零；④忽略管路压力损失与热量损失；⑤冷却器采用水或者空气冷却，因此假设冷却温度15～20℃；⑥ 不考虑波转子中冷热接触面的热传导；⑦换热器换热无热量损失。

3.2 热力参数定义

激波增压效率

压力恢复系数

(7)

气波机制冷系数

系统温降Dsys

Dsys=inlet-cold air(9)

气波机内部膨胀温降Dexp

Dexp=hp-cold air(10)

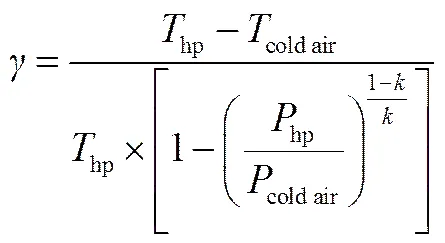
气波机内部制冷压比

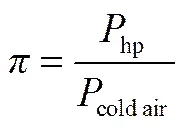
3.3 波转子冷凝系统热力学计算与分析

波转子冷凝系统-图见图10。进入系统的气体定压降温后进入气波机内膨胀获得最终冷凝分离的温度（cold air），冷凝液在过滤器中分离，脱湿干气进入换热器，定压升温后重新进入气波机，推动气波机内部低温气体排出通道，待低温气体排净后，脱湿干气占据波转子空间，最后被下一次入射的高压气体增压，排出波转子通道，实现脱湿干气压力能的恢复。

系统膨胀压比为1.55时，随着气波机入口温度降低，系统的冷凝温降大为提升（图11），但是由于系统制冷效率由设备本身因素决定，故依据式（8），气波机制冷温降降低。

图12为激波增压效率与脱湿干气压力恢复系数关系。系统膨胀比不变条件下，激波增压效率越高，脱湿干气的压力恢复能力越强。而系统膨胀压比越小，激波强度越弱，激波的非等熵性越低，激波增压效率越接近等熵压缩效率，系统压力恢复系数越大，脱湿干气压力恢复能力越强。

4 实验研究

气波制冷机是高效气波冷凝分离系统的核心部件，波转子以及各个端口的空间位置与大小是气波制冷机的核心参数。为了研究核心参数对系统制冷性能的影响，本文在数值计算与热力学计算的基础上搭建了实验平台，主要研究了系统转速与压比对系统制冷性能的影响。

4.1 实验流程

系统流程图见图13，采用低压螺杆压缩机提供气源，经过分离组件后预冷，预冷后的高压气体进入气波机内部膨胀降温，低温气体从低温排气端排出，进入分离器中脱湿，脱湿后的干气进入换热器中交换冷量，脱湿干气温度升高后，重新进入气波机内部，被下一阶段高压气体压缩，恢复脱湿干气压力能，排出系统。现场实验样机见图14。

4.2 实验结果及分析

本实验制冷膨胀比设计值为1.74，利用数值优化方法，设计各个端口的空间位置与大小。当系统实际制冷压比1.74运行时，改变气波机转速，最高制冷效率为63%，最大制冷温降为35 K，见图15、图16。但由于实验过程中，气波机进气温度不能维持恒定，会有稍许偏差，故导致最高效率点与最大温降点存在偏差。当改变系统压比时，系统效率明显下降，且偏差越大，制冷效率下降越严重，原因是当第1道激波S1（图3）从波转子通道内部移动至通道右端时，高温端口开启，如果压比变大，激波S1运动速度提高，则要求波转子提高转速。当高温口闭合时，要求高温气体排净，否则一部分未排净高温气体会产生反向压缩波，提高低温区的温度。从提高压比后的温降与效率曲线而言，系统仍存在对应的高效率点。

对比热力学分析，当系统膨胀压比提高时，脱湿干气压力恢复能力随即降低，见图17。系统膨胀比越大，激波强度越大，激波的非等熵性越突出，高压气体膨胀功损失越多，进而激波增压效率降低，脱湿干气压力恢复能力越弱。

考虑冷凝现象对于气波冷凝装置性能的影响，调整压缩机出口冷却风机送风量，改变分离储罐的进气温度，进而改变高压进气含湿量。高压进气口采集高压气体，利用色谱分析仪获得组分。固定气体膨胀压比为1.74，调整不同高压进气含湿量，测得气波机膨胀温降，见图18。

膨胀压比1.74时，不同含湿量条件下，最大温降点仍约为41 Hz，说明在此条件下凝结对于气波机端口设计影响不明显。凝结激波强度相对于高压入射激波强度偏弱。但是气波机温降随着含湿量增加明显降低，凝结潜热对于高效气波冷凝装置存在一定影响。

5 结 论

本文设计了高效气波冷凝装置，有效克服传统气波制冷热力学缺陷，利用激波增压特性，回收高压气体压力能用于恢复脱湿干气压力能；回收脱湿干气冷量，预冷下一循环高压进气，获得更低的脱湿温度，进一步提高系统脱湿性能。本文利用空气动力学理论，建立高效气波冷凝装置的波图，设计波转子内部波系运动关系；利用数值分析手段，预估与优化了各个喷嘴的尺寸；建立了高效气波冷凝整套装置的热力学模型，分析了整套冷凝装置的热力过程；最后通过实验获得了主要参数对制冷性能与脱湿干气压力恢复性能的影响，得到结论如下。

（1）本文建立的二维数值模型，可以有效反映波转子内部波系的匹配关系，优化了各个端口的空间布局与尺度，为搭建实验平台提供结构基础。

（2）通过整套装置热力学模型计算可得，回收脱湿干气低温资源，预冷下一循环高压进气，可以有效提高冷凝温度，进一步提高系统冷凝性能。提高激波增压效率可以提高脱湿干气压力恢复能力。

（3）实验表明，脱湿干气在系统内压力可以得到恢复，实验中最高压力恢复系数为0.9，且随着压比增大，压力恢复能力迅速降低。根本原因在于，压比越大，激波越强，激波压缩越偏离等熵压缩，压力能损失越大。故小制冷压比下干气压力能恢复效率高。

（4）高效气波冷凝装置依据内部结构参数，具有唯一最优设计点，压比、转速甚至背压的偏离都会引起制冷效率降低，结构参数连续可变是解决变工况的运行的有效手段。

（5）凝结激波产生不会严重影响气波机内部匹配，因为其强度远远小于高压入射激波强度，气波机最优匹配点仍不变。但是凝结潜热会对气波机制冷温降有一定影响。

符 号 说 明

A——高压喷嘴宽度一半，mm B——波转子通道宽度，mm C——高温口近端到基准线距离，mm cp——比热容，J·(kg·K)-1 D——低温口近端到基准线距离，mm d——含湿量，g·kg-1 E——回气口近端到基准线距离，mm Dhisen,Dhshock——分别为等熵焓变、激波焓变，J L——波转子通道长度，mm N——一周期喷嘴个数，个 n——波转子转速，r·min-1 P——绝对压力，Pa P1, P2, P3, P4——分别为高压端、高温端、回气端和低温端压力，Pa Pcold air, Php, PmiddleP, Poutletisen——分别为冷气出口压力、高压进口压力、中压端口压力和等熵压缩出口压力，Pa Pinlet, Poutlet——分别为系统进气压力和激波压缩出口压力，Pa R——波转子通道1/2中径，mm Su, Sv, ST, SΦ——分别为动量方程x、y方向的广义源项，能量方程广义源项和广义源项 T——静温，K Tcold air,∆Texp,Thp,Tinlet,∆Tsys——分别为冷气温度、气波机内膨胀温降、高压进口温度、系统进口温度和系统温降，K T1, T2, T3, T4——分别为高压端、高温端、回气端和低温端温度，K u, v, w——速度分解3个方向，m·s-1 Γ——广义扩散系数 γ——膨胀制冷效率 δ——各个端口与波转子间隙，mm η——激波增压效率 λ——热传导系数，W·(m·K)-1 π——气波机膨胀压比 σ——压力恢复系数 F——通用变量

References

[1] 胡大鹏, 王荧光, 任文文, 等. 导流锥式超声速旋流分离装置流动特性[J]. 化工学报, 2016, 67(6): 2417-2425.HU D P, WANG Y G, REN W W,Flow characteristic of supersonic gas separator with diversion cone[J]. CIESC Journal, 2016, 67(6): 2417-2425.

[2] AKBARI P, MUELLER N. Wave rotor research program at Michigan State University[J]. International Journal of Science Education, 2013, 75(9): 627-641.

[3] AKBARI P, NALIM R. Review of recent developments in wave rotor combustion technology[J]. Journal of Propulsion & Power, 2009, 25(4): 833-844.

[4] AKBARI P, NALIM R, MUELLER N. A review of wave rotor technology and its applications[J]. Eng. Gas Turbines Power, 2006, 128(4): 717-735.

[5] KENTFIELD J. Wave rotors and highlights of their development[J]. AIAA Paper, 1998, 3248: 1998.

[6] IANCU F, MÜLLER N. Efficiency of shock wave compression in a microchannel[J]. Journal of Microfluid and Nanofluid, 2005, 2(1): 50-63.

[7] LEI Y, ZHOU D S, ZHANG H G. Investigation on performance of a compression-ignition engine with pressure-wave supercharger[J]. Energy, 2010, 35(1): 85-93.

教材是教师教学的帮手，也是规范教学和传承教育内容的保证。礼仪课程的教材种类繁多，但很少有教材完全符合教学需求，只是部分对教学有价值，如何汲取有价值的部分，使其固化为适合本校学生的教材，这对所有礼仪教师都是挑战。因此，性质相同、教学体系相似的院校的旅游礼仪教师可合作共同编制礼仪教材，根据本校学生的实际情况，将理论与实践内容以文字的形式展现，但必须遵循以下几个原则：结合院校的性质，教材内容符合学生的可接受性；摒弃学科中心主义的思想，建立新的教材内容体系框架；反映时代特征，体现职业适用性价值；体现教材的教育性价值，使学生多方面获益[9]。在此基础上，规范、完善理论及形体实践教学内容。

[8] SPRING P, ONDER C H, GUZZELLA L. EGR control of pressure-wave supercharged IC engines[J]. Control Eng. Pract., 2007, 15(12): 1520-1532.

[9] DAI Y, HU D P, DING M X. Study on wave rotor refrigerators[J]. Front. Chem. Eng., 2009, 3(1): 83-87.

[10] WELCH G, JONES S, PAXSON D. Wave-rotor-enhanced gas turbine engines[J]. Journal of Engineering for Gas Turbines & Power, 2013, 119(2): 469-477.

[11] DAI Y Q, ZOU J P, WU J T,Unsteady behavior of real gas in wave rotor refrigerators[J]. Adv. Mater. Res., 2011, 236/237/238: 1516-1522.

[12] LIU P, ZHU Y, ZHAO J,Investigation and optimization of waves motion behavior in pressure oscillating tube[J]. Exp. Therm. Fluid Sci., 2013, 50(7): 193-200.

[13] DAI Y Q, ZOU J P, ZHU C,. Thermodynamic analysis of wave rotor refrigerators[J]. Therm. Sci. Eng. Appl., 2010, 2(2): 021011-1-6.

[15] PAXSON D E. A numerical model for dynamic wave rotor analysis[C]//AIAA Joint Propulsion Conference and Exhibit. 31st. San Diego, California: AIAA, 1995: 2800.

[16] PIECHNA J. Numerical simulation of the pressure wave supercharger—effects of pockets on the comprex supercharger characteristics[J]. The Archive of Mechanical Engineering, 1998, 45(4): 305-323.

[17] PIECHNA J, LISEWSKI P. Numerical analysis of unsteady two dimensional flow effects in the comprex supercharger[J]. The Archive of Mechanical Engineering, 1998, 45(4): 341-351.

[18] SELEROWICZ W, PIECHNA J. Comprex type supercharger as a pressure-wave transformer flow characteristics[J]. The Archive of Mechanical Engineering, 1999, 46(1): 57-77.

[19] ELLOYE K J, PIECHNA J. Influence of the heat transfer on the operation of the pressure wave supercharger[J]. The Archive of Mechanical Engineering, 1999, 46(4): 297-309.

[20] PIECHNA J. A two-dimensional model of the pressure wave supercharger[J]. The Archive of Mechanical Engineering, 1999, 46(4): 331-348.

[21] PIECHNA J. Comparison of different methods of solution of Euler equations in application to simulation of the unsteady processes in wave supercharger[J]. The Archive of Mechanical Engineering, 1998, 45(2): 87-106.

[22] EIDELMAN S. The problem of gradual opening in wave rotor passages[J]. Propul. Power, 1985, 1(1): 23-28.

[23] LAROSILIERE L M. Wave rotor charging process — effects of gradual opening and rotation[J]. Propul. Power, 1995, 11(1): 178-184.

[24] OKAMOTO K, NAGASHIMA T. Visualization of wave rotor inner flow dynamics[J]. Journal of Propulsion and Power, 2007, 23(2): 292-300.

[25] PATANKAR S V. Numerical Heat Transfer and Fluid Flow[M]. New York: Mc-Graw-Hill, 1980: 15.

[26] LEER B V. Upwind-difference methods for aerodynamics problems governed by the Euler equations of gas dynamics[J]. Large-scale Computations in Fluid Mechanics, 1985, 22: 327-336.

[27] 刘培启, 徐思远, 王泽武,等. 偏角对气波制冷机制冷效率的影响及预测[J]. 化工学报，2014, 65(11): 4271-4277. LIU P Q, XU S Y, WANG Z W,Influence of offset angle on refrigeration efficiency of gas wave refrigerator and prediction for optimal offset angle[J]. CIESC Journal, 2014, 65(11): 4271-4277.

Flow and thermodynamic properties of efficient gas wave refrigeration plant

YU Yang, LIU Peiqi, WANG Yunlei, LENG Chuang, ZHAO Yiming, WANG Jingxian, HU Dapeng

(School of Chemical Machinery, Dalian University of Technology, Dalian 116023, Liaoning, China)

With the theory of aerodynamics, the efficient gas wave condensation graph was established. To optimize the gas wave condensation graph and estimate the internal structure parameters of the device, the two-dimensional periodic boundary model was adapted and the ideal gas as the medium was used to numerical simulate the flow and temperature field of the efficient gas wave condensation separator. The thermodynamic model of condensing system was established and its thermodynamic properties were analyzed. At the same time, the experimental platform was built, and the main parameters of the device were studied. The experimental results shows: by using the shock wave to recycle the pressure energy of the high pressure admission, the pressure energy of the drying gas can be highly recovered. By recycling the cooling capacity of the drying gas and pre-cooling the next high pressure admission circulation, the lower condensation temperature can be obtained. The refrigeration efficiency of this device exists the single-valued optimal point. The internal expansion efficiency of efficient gas wave condensation is about 63% and the maximum of the drying gas pressure can be recovered to 90%, which decreases with the increase of the pressure ratio.

gas wave condensation; fluid dynamics; numerical simulation; shock wave; thermodynamic process; design

10.11949/j.issn.0438-1157.20170267

TQ 051.1

A

0438—1157（2017）08—3039—10

胡大鹏。第一作者：于洋（1985—），男，博士研究生。

国家自然科学基金项目（21476036）；中国国家科技重大专项（2016ZX0566005-002）。

2017-03-21收到初稿，2017-06-01收到修改稿。

2017-03-21.

Prof.HU Dapeng, hudp@dlut.edu.cn

supported by the National Natural Science Foundation of China (21476036) and the Major Special Project (2016ZX0566005-002).