圆柱形锂离子电池模组微通道液冷热模型
2017-08-09赵春荣曹文炅董缇蒋方明
赵春荣,曹文炅,董缇,蒋方明
圆柱形锂离子电池模组微通道液冷热模型
赵春荣1,2,曹文炅1,董缇1,2,蒋方明1
(1广东省新能源和可再生能源研究开发与应用重点实验室,中国科学院可再生能源重点实验室,中国科学院广州能源研究所先进能源系统研究室,广东广州 510640;2中国科学院大学,北京 100049)
针对电动汽车电堆的热管理系统,建立了包含71节18650型锂离子电池的电池模组的微通道液冷热模型。该模型集总处理单电池热过程、电池生热基于实测结果,模型还特别考虑了电池间导热。基于该模型,模拟研究了放电倍率、冷却液入口流速、电池间接触面积以及电池与水冷管外壁接触面积对电池模组热行为的影响。模拟结果证实了该微通道液冷方案对动力电池模组热管理的有效性,并且发现:放电倍率的增加会使电池模组内单电池温度增加、模组内温度一致性变差;增大冷却液流量可以显著降低电池模组的温度,并改善其温度一致性;增大电池间接触面积可略微提升电池模组温度一致性,但对控制其最高温度作用有限;增大电池与液冷管外壁接触面积可显著降低电池模组内电池的最高温度,但会使其温度一致性变差。
锂离子电池;热模型;微通道;计算机模拟;传热
引 言
电动汽车(electric vehicle,EV)在近几年进入高速发展期,锂离子电池因其高能量密度、长循环寿命等特性而被电动汽车广泛采用。动力锂离子电池使用过程中需要面对复杂的运行工况和环境条件,有效的电池热管理系统(battery thermal management system,BTMS)是保证其良好性能(包括安全性)的基础[1]。
锂离子电池的最佳工作温度因电池类型不同略有差异,一般来说,电池最佳工作温度区间为25~40℃。同时,为了确保动力电池堆(组)的整体性能,电堆内各单电池间温差应尽可能小。目前,文献报道的电堆热管理技术方案主要有:空冷[2-5]、液冷[6-7]、相变材料(phase change materials,PCM)[8]、热管[9]。液冷方案因其高效、可靠等特性[10]而受到广泛关注。Jin 等[11]采用的液冷冷板中设置了斜肋微通道,由此造成的流体自扰动增强了冷板换热能力。Rao等[12-14]针对3种不同的微通道液冷方案,通过数值模拟探讨了通道数目、流动方向、流动速度和环境温度对于电堆热行为的影响。Basu 等[15]数值模拟了18650型 NCA(镍钴铝)三元锂离子电池堆的微通道液冷,证实了其冷却方案的有效性。
数值建模是研究电池热行为、开发先进BTMS的重要手段[16]。根据模型所描述的物理过程,可将模型分为热模型[17]、电热模型[18-19]和电化学-热模型[20-21]。热模型只求解能量守恒方程;电热模型将能量守恒方程和基于等效电路的电荷守恒方程耦合求解;电化学-热模型考虑电、化学及热过程的多物理场耦合,对电及化学过程进行精细刻画以确定能量守恒方程中的源项,热模型所描述的温度场通过物性参数来影响电化学模型中的电极反应与电荷传递。考虑到热模型所涉及的物理过程最少,在计算量方面有优势[22-24],因此更可能用于BTMS的模拟仿真。在电堆热模型建立的过程中,需要考虑电池生热、散热和热物性参数的处理。Cho 等[25]指出电池生热一部分通过导热、对流和辐射向外部散失,另一部分用于自身内能增高(显热),并讨论了各部分所占权重。Gu 等[26]从能量守恒出发,详细探讨了电池的生热机理,总结电池生热主要分为电化学反应热、内部阻抗热、由离子浓度梯度引起的混合热和由相变反应引起的相变热。Chen 等[27]系统总结各种圆柱电池热物性参数的计算方法,并提出改进方案以解决拟合度不够引起的误差。Wang 等[17]在电池模组热模型开发中对单电池的热物性参数进行了集总处理。
当前,电动汽车电堆模型的开发因计算量等问题,鲜有直接针对电池数量庞大的动力电池堆建立数值模型的工作报道;基于圆柱形电池的动力电池堆而建立热模型进行液冷微通道设计优化的工作在公开文献更不多见;单体电池间的热交换在电堆模型中也少有考虑。本文针对18650型电池组成的动力电池堆的微通道液冷系统,建立了包含71节电池的电池模组的热模型。该热模型集总处理圆柱电池单体内的热过程,基于实验结果建立单电池的生热模型,还特别考虑了相邻电池间的导热。模拟研究了放电倍率、冷却流体流速、电池间接触面积以及电池与液冷通道外壁接触面积对该电池模组热行为的影响。
1 数学-物理模型
1.1 物理模型
1.1.1 电池单体的集总热模型 模型考虑的动力电池模组由某商用18650型 NMC(镍钴锰)三元锂离子电池单体构成。18650电池的内部结构如图1所示,主要包括:负电极集流体(铜箔)、负电极、隔膜、正电极、正电极集流体(铝箔)和外壳。正极、隔膜和负极为多孔材料,孔隙内充斥着电解液。外壳(can)材质为钢,外表面包覆绝缘材料。
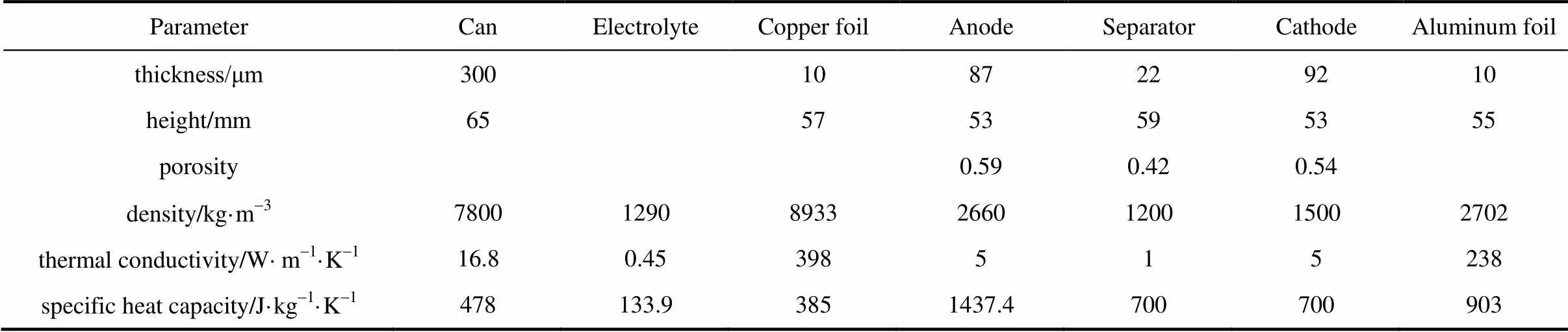
表1 电池材料的热物性及单电池的几何参数[20,30-32]
常规情形下,单体电池内部结构细节对于电堆整体的热行为影响较小[28-29],因此可以对电池的温度及热物性参数集总处理:忽略电池内部的温度差异、做平均化处理;电池热物性参数由各种材料组分加权平均确定。表1给出了电池材料的热物性及单电池的几何参数。
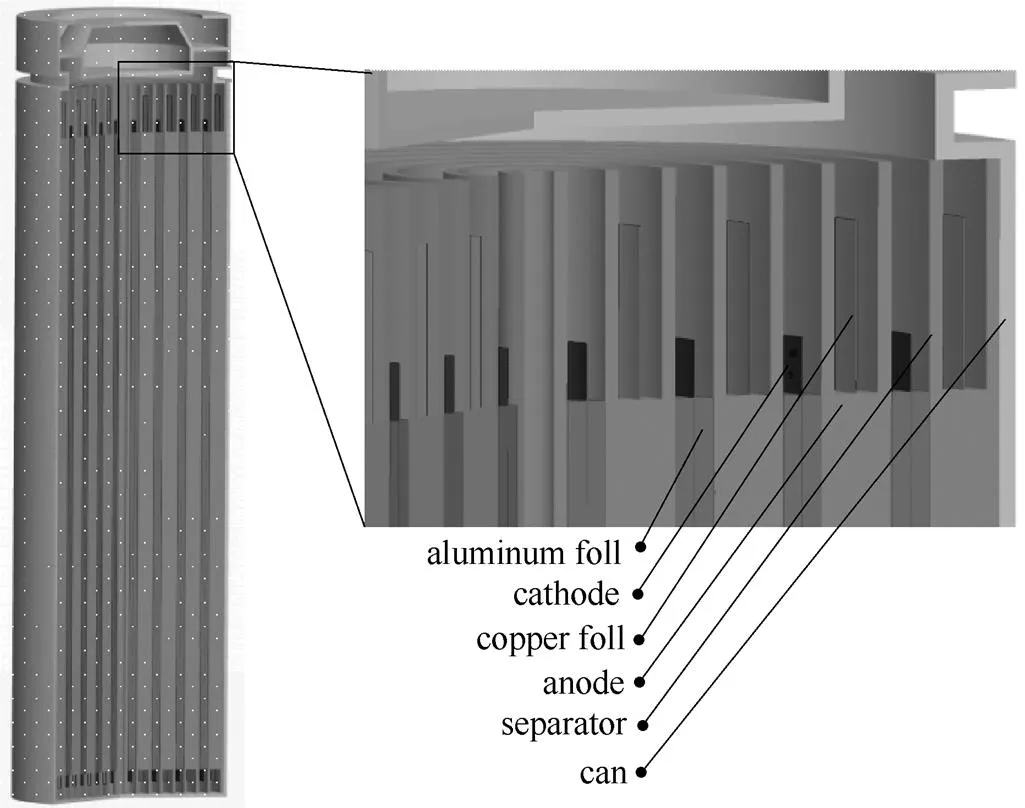
图1 18650型号NMC锂离子电池结构

表2 子计算域内的控制方程
电池单体密度及热容的当量值用式(1)计算[33]
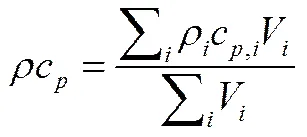
电池有效热导率计算公式为[34]
(2)
其中,为密度,c为体积热容,为体积,为热导率,为厚度,为材料组分标识。
1.1.2 电池模组物理模型 Tesla电动汽车Model S型号因其出色的续航里程(>400 km)、运行可靠等而广受关注。其电堆由74×6×167104节Panasonic公司的NCA三元锂离子电池构成,最高电压400 V,采用微通道液冷进行冷却。本文借鉴其电堆结构,但仅考虑实际动力电池堆的一个模组,其由71节18650型NMC锂离子电池并联而成。铝质微通道扁管穿插于电池间,与每个单电池均紧密接触;扁管在与单电池接触处适当弯曲,从而保证与电池具有一定的换热面积;微通道扁管内通冷却液。模组物理模型如图2所示,微通道扁管截面上下壁厚为1 mm、侧面壁厚为0.5 mm,内部流道高度为63 mm、宽度为2 mm,电池间接触面的圆周角度为1、电池与微通道接触面的圆周角度为2。
1.2 数学模型
1.2.1 控制方程 计算区域包括3个子计算域:NMC三元锂离子电池、铝质微通道固体壁和通道内冷却液。各子域做如下假设:电池视为含内热源的均一固体;微通道内充满持续流动冷却液且为单相流体流动;流体流动为层流;冷却液物性近似参照标准状态下水的物性。模型求解的主要控制方程如表2所示。
1.2.2 电池单体生热模型 该商用18650型NMC三元锂离子电池容量为1.5 A·h。根据Bernardi[22]提出的生热速率模型,电池单体的产热量为
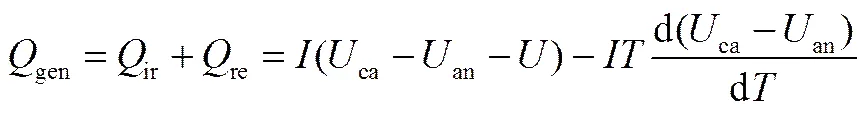
其中,ir为不可逆热,re为可逆熵热;为电池温度;和分别为工作电流和工作电压。正负极开路势caan及其温度依变关系采用文献数 据[20,35-36]。将电池置于25℃的恒温箱中,使用Arbin BT2000测定0.5C、1C、3C和5C放电倍率下的放电曲线。根据式(6),计算得出单电池在不同放电倍率下的生热速率(gen),如图3所示。图中DOD代表放电深度(depth of discharge)。
图2 电池模组及其计算网格示意图
Fig.2 Lithium-ion battery module and schematic of numerical mesh
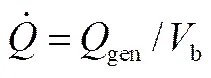
式中,b代表电池单体体积。
1.2.3 电池单体间的导热模型 电堆装配时会在电池间布置导热胶,以改善电池间接触状况。假设电池间的接触面为一定圆周角度的电池侧表面。由此,电池间的换热量1可表示为

其中,近似考虑为电池有效热导率;1是电池间接触面积,以电池间接触面的圆周角度1来量度,如图2所示;Δ为电池之间的温差;假设式(8)中代表电池中心温度,则电池间传热距离1近似为18650圆柱电池的直径18 mm。
图3 25℃环境下不同放电倍率下的单电池生热速率
Fig.3 Heat generation rate for single battery with different discharge C-rates at 25℃ environment
1.2.4 电池与液冷管外壁间的导热模型 电池与微通道液冷管道以一定角度的电池侧表面接触,通过导热方式与液冷管外壁进行热交换,故电池与液冷管外壁的换热量2为
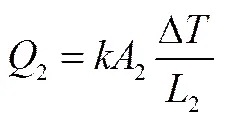
忽略电池与管外壁间的接触热阻,仍近似考虑为电池有效热导率;2是电池与液冷管外壁的接触面积,以电池与液冷管外壁接触面的圆周角度2来量度,如图2所示;Δ为电池与管外壁间的温差;2则是电池中心距液冷管外壁的传热距离,可近似为18650圆柱电池的半径9 mm。
1.2.5 初始及边界条件 液冷电堆内部结构紧凑、外包绝缘材料。忽略电池模组与周围空气的自然对流和辐射传热,即除流体进出口边界外,所有其他边界为绝热边界;流体在微通道内壁无滑移;所有电池初始荷电状态SOC(state of charge)100%(SOC1DOD);电池模组的初始温度、环境温度和冷却流体的入口温度均设为25℃;冷却液入口流速为0.1 m.s-1或0.5 m.s-1,对应的Reynolds数分别是427.7和2138.6,证实了前述流体层流假设的可行;流体出口为定压边界,相对压力为0。
2 数值模拟结果及分析
利用FLUENT的用户自定义函数(user defined function,UDF),将热源项和物性等编程计算,然后耦合求解传热和流体流动方程。FLUENT基于有限体积方法(finite volume method,FVM)求解偏微分方程组。空间导数项采用二阶迎风差分格式、时间导数项采用全隐差分格式,SIMPLE(semi-implicit method for pressure linked equation)方法用于处理压力-速度的耦合。
图2还示出了计算网格,为了确保数值计算结果的准确性,基于Richardson extrapolation方法[37]进行网格独立性验证。考虑出口截面流体的平均温度(mass-weighted average static temperature),分别对致密程度不同的3种网格(22240、69795和218526)和跨度不同的3种时间步长(0.1 s、0.5 s和1.0 s)进行了数值求解,并根据模拟结果外推得到精确解。结果表明依据本文采用网格及时间步长所得的计算结果与外推的精确解偏差小于1%。
计算所考虑的电池放电倍率:0.5C、1C、3C和5C;冷却液入口流速:0.1m·s-1和0.5 m·s-1;电池间接触面的圆周角1:0°(即不考虑电池间导热)、4°、8°和12°;电池与液冷管壁接触面的圆周角2:10°、20°、30°和40°。
2.1 放电倍率对电池模组热行为的影响
电动汽车实际行驶中有不同功率需求,需要电堆以不同倍率进行放电。在冷却液入口流速0.1 m·s-1、电池间接触面圆周角18°以及电池与液冷管壁接触面圆周角240°下,数值模拟了该电池模组在0.5C、1C、3C、5C放电倍率下的放电过程。

图4 不同放电倍率(0.5C,1C,3C,5C)下电池模组剖面内的温度分布(冷却剂入口流速0.1m·s-1)
图4为电池模组剖面的温度云图。首先,在同一放电倍率下,对于图示的4个DOD值(DOD0.1,0.3,0.6,0.9),电池模组中的电池温度随DOD的增加先升高后降低,与电池的生热率跟DOD的依变关系(图3)定性一致。其次,同一放电深度(DOD)下,电池模组中的电池温度随放电倍率的增加而升高。以0.5C放电倍率为例,电池模组在DOD0.3时整体温度达到峰值,此时该模组中电池温度最高为298.6 K。在DOD0.3时,与0.5C放电相比, 1C、3C和5C放电下该模组中电池最高温度分别为299.3、303.9和 309.5 K。
由图4还可看出,微通道中流体沿程温度逐渐升高,因此,处于下游位置电池温度要高于上游电池温度。对于位于U形通道内侧的单电池,上下游会有2~4节电池相邻而发生热交换[式(8)];而位于通道外侧的电池,上下游只有1~2节电池相邻。因此,该电池模组中温度最低的电池位于流体通道进口端的外侧、温度最高的电池位于流体通道出口端的外侧。
衡量动力电池BTMS有效性的两个重要指标为电堆中的最高温度和电堆内单体电池间的最大温差。图5示出了不同放电倍率下,电池模组内最高温度和最大温差随放电深度(DOD)的演化。由图5(a)可看出,该模组内的电池最高温度在放电开始后升高较快、中期略有降低、后期又会升高,整体变化近似倒S形。电池生热分流为两部分:电池内的热累积和热散失。热散失主要是冷却流体对流散热。在定流速下,流体对流散热量相对固定。因此,电池的温度随DOD变化(反映了电池内热累积情况)而呈现出与电池生热率曲线(图3)定性相似的变化趋势。
0.5C和1C的放电倍率时,电池最高温度均低于300 K;3C和5C放电倍率下,电池模组中电池最高温度分别为304.5 K和311.6 K。由图5(b)可以看出,该模组内的电池间最大温差与DOD关系在变化趋势上类似模组内电池最高温度与DOD的关系。在0.5C和1C放电时,该模组内的电池间最大温差变化小,其值始终在0.5 K以下;而3C和5C放电时,电池间最大温差分别为1.8 K和3.7 K。
结合图5(a)、(b)还可看出,低倍率放电(0.5C和1C)电池模组的热状况良好;高放电倍率(3C和5C)会使电池的温度升高较大,有脱离电池最佳运行温度窗口(25~40℃)的趋势,同时使得该电池模组的温度一致性变差。
微通道中冷却液因汲取电池的热量沿程温度会逐渐升高,图6示出的冷却液温度曲线证实了这一判断。不同放电倍率下的流体温度沿程升高;在5C放电时,冷却液在出口处温升超过3 K。同时由于微通道结构存在U形转折区域,该区域电池数密度要小于其他区域,故使得该区域冷却流体温度上升速率减缓。
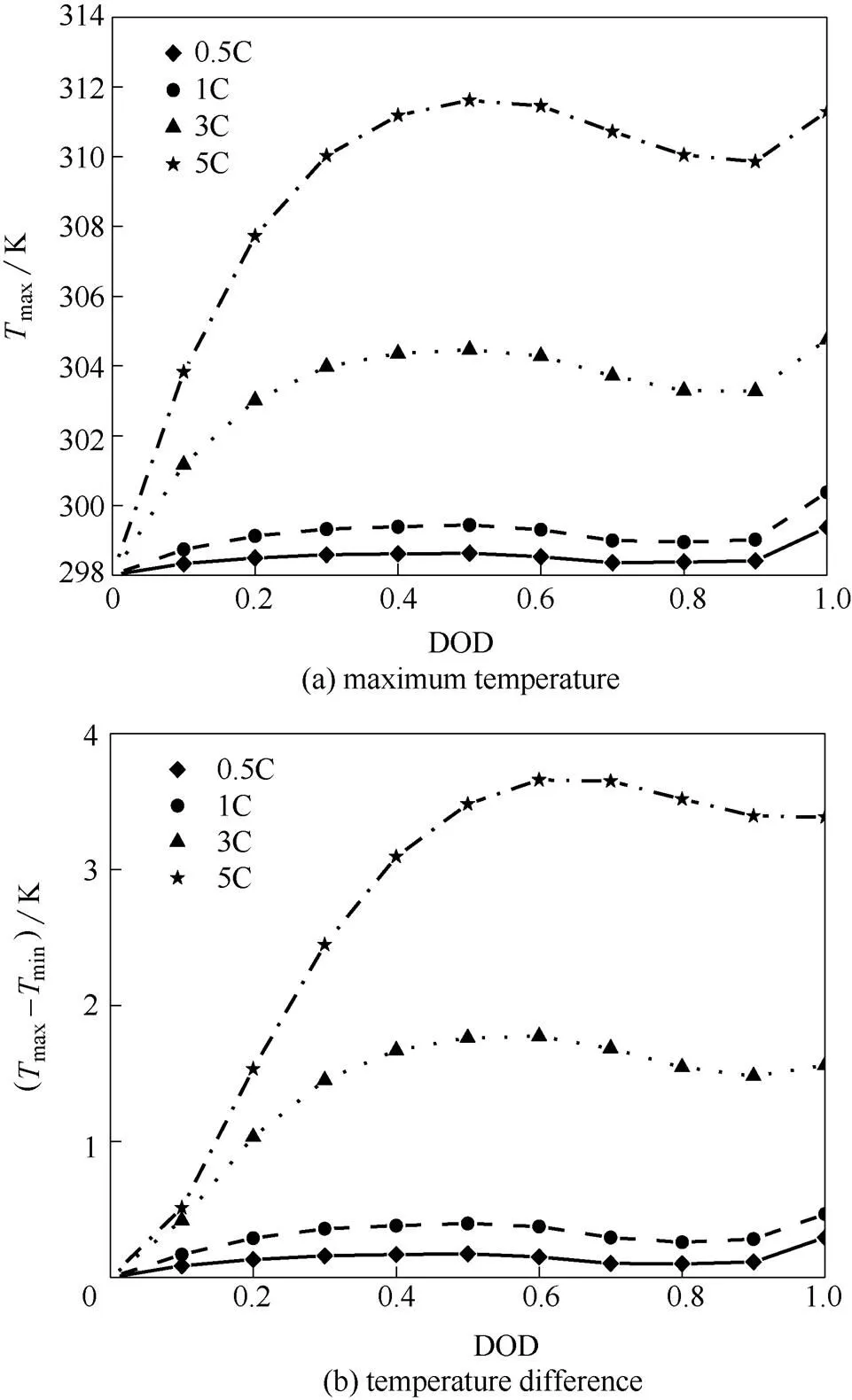
图5 流体入口速度0.1m·s-1下电池模组内最高温度和最大温差在放电过程中的演化
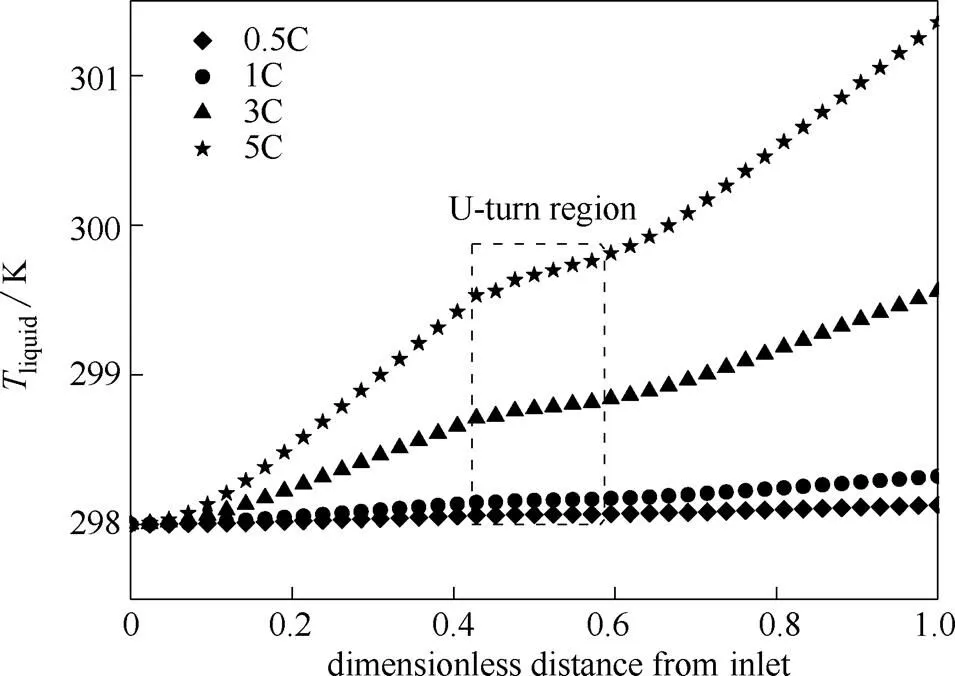
图6 冷却液沿程温度(流体入口速度0.1 m·s-1)
2.2 冷却液入口流速对电池模组热行为的影响
增加流体流速会增强对流换热,然而,流速增加也意味着泵功率的增大。因此,BTMS应尽可能选取合适的流体流速,在较少泵功消耗的条件下实现电堆的有效散热。在5C放电倍率、18°和240°下,对电池模组在0.1 m·s-1和0.5 m·s-1的冷却液入口流速下的热行为进行模拟分析。
图7给出了不同入口流速下,电池模组的最高温度max和最大温差maxmin随放电深度(DOD)的演化曲线。由图7(a)可看出,不同入口流速下,电池模组中的最高温度在放电起始阶段迅速升高,随后在DOD为0.5~0.9之间略有降低,在放电结束阶段又有回升。0.1 m·s-1和0.5 m·s-1的流速对应放电过程的最大max分别为311.6 K和308.8 K。而在图7(b)中,流速0.1 m·s-1时最大maxmin为3.7 K,0.5 m·s-1时的最大温差则始终位于1 K以下。因此,BTMS在0.5 m·s-1流体入口流速时对电堆模组的热管理更为有效。

图7 5C放电倍率下电池模组内最高温度及最大温差的演化
2.3 电池间接触面积对电池模组热行为的影响
电堆中单体电池间的接触面积对BTMS的有效性有影响。电池成组时会通过在电池间设置导热胶等方式增加接触面积,以利于电池间的热交换。在5C放电倍率、0.1 m·s-1的流体入口流速以及电池与液冷管壁接触面圆周角2=40°条件下,探讨电池间接触面圆周角10°(即不考虑电池间导热)、4°、8°和12°时电池模组的热行为。
图8示出了不同1条件下,电池模组的最高温度max和最大温差maxmin随放电深度(DOD)的演化曲线。由图可知4条max-DOD曲线几乎重合;细节图显示4°、8°和12°曲线相比于0°,max略有降低;进一步对比三者发现,8°和12°曲线相比4°略低,但彼此间几无差别。这是因为随着电池间接触面积的增大,温度最高的电池(位于微通道出口端外侧)向上游电池导热能力增强,自身温度降低;另一方面,其上游电池温度的上升增大了其与当地流体的换热能力,使流至该电池附近的流体温度上升,由此造成的更小的温差反而减弱了该电池向流体的传热能力。当电池间接触面积增大到一定程度后,这两种相反的效应相互抵消,阻止max的进一步降低,并使不同接触面积的max-DOD曲线趋于近似重合。图8(b)显示电池模组中最大温差随1增大而减小,其中对比10°和112°的结果发现,两者最多相差0.3 K左右。因此,电池间的接触面积增大对电池模组的整体温度影响较小,但电池模组内的温度一致性有一定程度改善。
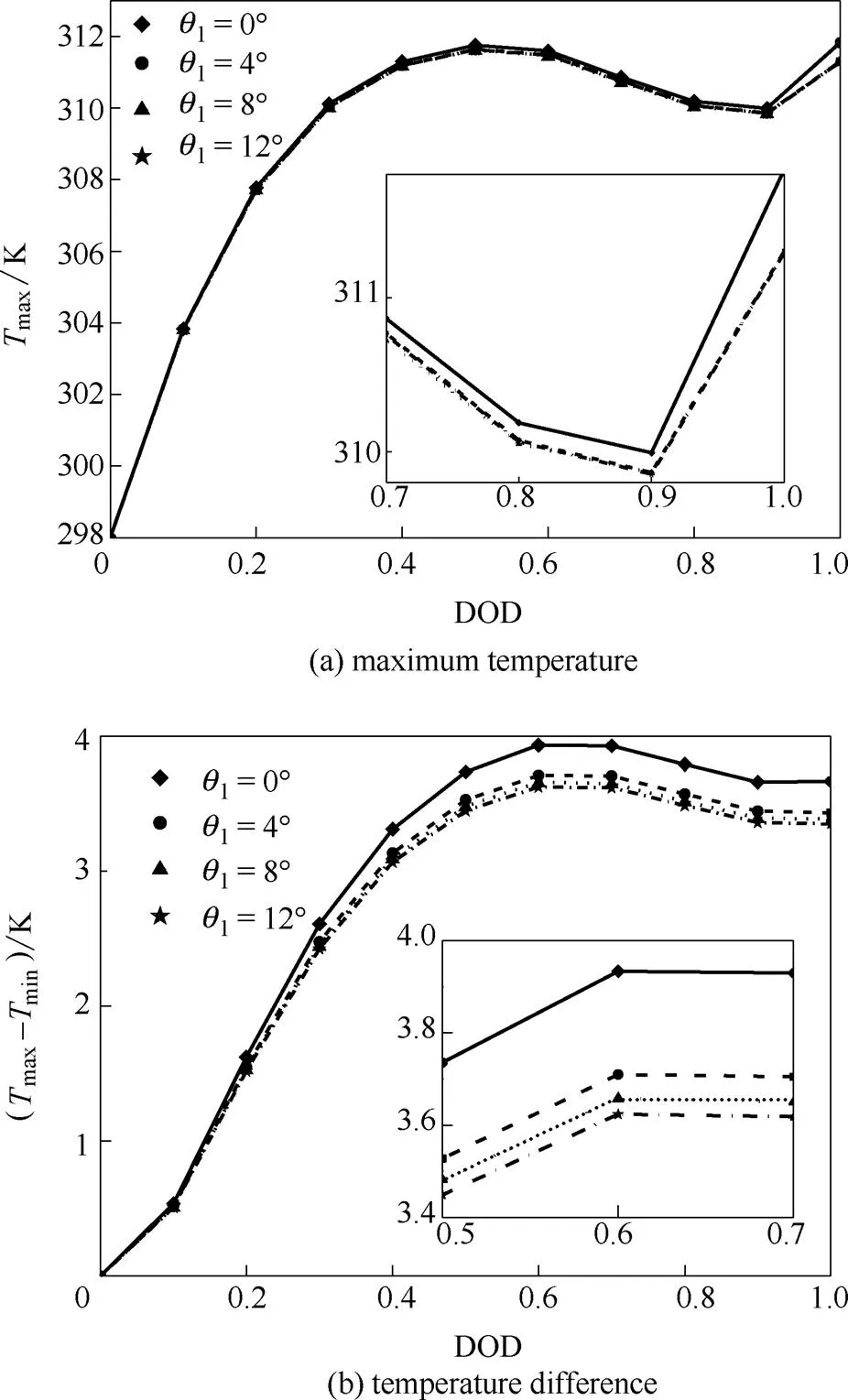
图8 不同θ1下电池模组内最高温度及最大温差的演化
2.4 电池与液冷管壁接触面积对电池模组热行为的影响
电池与铝质微通道装配过程中出现的接触不良或微通道扁管变形等均会导致接触面的增减,有必要探究不同电池与液冷管壁接触面积对电池模组温升及其温度一致性的影响。
由图9(a)可看出,电池模组的最高温度max在放电过程中随2的增大而减小。210°时,max最大为329.8 K;220°时为318.4 K,30°时为313.9K,40°时为311.6 K。图9(b)显示最大温差在放电过程中随2增大而增大。210°时,maxmin最大为2.3 K;220°、30°和40°时分别为3.2、3.5和3.7 K。即增大电池与液冷管壁接触面积可以显著降低电池模组的最高温度,但同时会使模组内温度一致性变差。因此,实际应用中应根据不同电池的温度特性权衡选取合适的接触面积。

图9 不同θ2下电池模组内最高温度及最大温差的演化
3 总结与结论
本文针对电动汽车电堆的热管理系统,建立了包含71节18650型单体NMC锂离子电池的电堆模组的微通道液冷热模型。该模型集总处理电池单体的热过程、实验确定电池单体不同放电倍率的生热,并且对模组内单体电池间的换热进行了较细致的处理。随后,运用该模型对电池模组在不同放电倍率、不同冷却液入口流速时的热行为进行了模拟研究,还探讨了电池间接触面积和电池与微通道管外壁接触面积对电池模组热行为的影响。
模拟结果证实了微通道液冷方案对动力电池模组热管理的有效性。当放电倍率不大于5C,流体入口速度不小于0.5 m·s-1,电池间接触面圆周角1和电池与液冷管外壁接触面圆周角2分别为8°和40°时,电池模组的最高温度及模组内温度一致性都能得到很好控制。并且发现:
(1)放电倍率的增加会使电池发热量增大,电池模组内单电池温度升高、模组内温度一致性变差。在冷却流体温度为25°C及入口流速0.1 m·s-1、18°和240°、5C放电倍率时,电池单体生热率为3 W左右,电池模组内电池温度最高达311.6 K,电池间最大温差可达3.7 K。
(2)增大冷却液流量可以显著降低电池模组的温度,并改善其温度一致性。5C放电倍率、18°和240°、流体的入口流速增大到0.5 m·s-1,电池模组内最大温升控制在11 K以内,电池间最大温差小于1 K。
(3)增大电池间接触面积可略微提升电池模组温度一致性,但对控制其最高温度作用有限。在5C放电倍率、冷却流体入口流速0.1 m·s-1、240°时,112°相比于0°可将模组内最大温差降低0.3 K左右。
(4)增大电池与液冷管外壁接触面积可能显著降低电池模组内电池的最高温度,但会使其温度一致性变差。在5C放电倍率、入口流速0.1 m·s-1、18°时,240°相比于10°可将模组内电池最高温度降低18.2 K,但同时使电池间最大温差升高2.3 K。
数值模拟的算例及模拟结果亦说明模型开发的成功,该模型进一步开发后将用于实际电动汽车动力锂离子电池电堆热行为的模拟研究、设计优化动力电池堆的热管理系统。
符 号 说 明

A1——电池间接触面积,m2 A2——电池与水冷管壁接触面积,m2 cp——电池热容,J·kg-1·K-1 I——电流,A k——电池热导率,W·m-1·K-1 L——电池组分厚度,m L1——电池间传热距离,m L2——电池中心距液冷管传热距离,m P——压强,Pa Q——热量,W ——电池体积生热率,W·m-3 Q1——电池间换热量,W Q2——电池与液冷管壁换热量,W T——电池温度,K t——时间,s U——电压,V u——速度,m·s-1 V——体积,m3 θ1——电池间接触面的圆周角度,(°) θ2——电池与液冷管壁接触面的圆周角度,(°) ρ——密度,kg·m-3 下角标 an——阳极 b——电池 ca——阴极 gen——电池生热 i——电池材料组分标识 ir——不可逆 re——可逆
References
[1] 赵阳, 黄震雷, 周恒辉. 纯电动汽车动力电池系统的发展现状 [J]. 新材料产业, 2015, (6): 37-41. ZHAO Y, HUANG Z L, ZHOU H H. The development status of pure electric vehicle power battery system [J]. New Material Industry, 2015, (6): 37-41.
[2] PESARAN A A. Battery thermal models for hybrid vehicle simulations [J]. Journal of Power Sources, 2002, 110 (2): 377-382.
[3] LI X S, HE F, MA L. Thermal management of cylindrical batteries investigated using wind tunnel testing and computational fluid dynamics simulation [J]. Journal of Power Sources, 2013, 238: 395-402.
[4] SAW L H, YE Y H, TAY A A O,. Computational fluid dynamic and thermal analysis of lithium-ion battery pack with air cooling [J]. Applied Energy, 2016, 177: 783-792.
[5] WANG T, TSENG K J, ZHAO J Y. Development of efficient air-cooling strategies for lithium-ion battery module based on empirical heat source model [J]. Applied Thermal Engineering, 2015, 90: 521-529.
[6] PENDERGAST D R, DEMAURO E P, FLETCHER M,. A rechargeable lithium-ion battery module for underwater use [J]. Journal of Power Sources, 2011, 196 (2): 793-800.
[7] YANG X H, TAN S C, LIU J. Thermal management of Li-ion battery with liquid metal [J]. Energy Conversion and Management, 2016, 117: 577-585.
[8] RAO Z H, HUO Y T, LIU X J,. Experimental investigation of battery thermal management system for electric vehicle based on paraffin/copper foam [J]. Journal of the Energy Institute, 2015, 88 (3): 241-246.
[9] RAO Z H, WANG S F, WU M C,. Experimental investigation on thermal management of electric vehicle battery with heat pipe [J]. Energy Conversion and Management, 2013, 65: 92-97.
[10] CHEN D F, JIANG J C, KIM G H,. Comparison of different cooling methods for lithium ion battery cells [J]. Applied Thermal Engineering, 2016, 94: 846-854.
[11] JIN L W, LEE P S, KONG X X,. Ultra-thin minichannel LCP for EV battery thermal management [J]. Applied Energy, 2014, 113: 1786-1794.
[12] HUO Y T, RAO Z H, LIU X J,. Investigation of power battery thermal management by using mini-channel cold plate [J]. Energy Conversion and Management, 2015, 89: 387-395.
[13] ZHAO J T, RAO Z H, LI Y M. Thermal performance of mini-channel liquid cooled cylinder based battery thermal management for cylindrical lithium-ion power battery [J]. Energy Conversion and Management, 2015, 103: 157-165.
[14] QIAN Z, LI Y M, RAO Z H. Thermal performance of lithium-ion battery thermal management system by using mini-channel cooling [J]. Energy Conversion and Management, 2016, 126: 622-631.
[15] BASU S, HARIHARAN K S, KOLAKE S M,. Coupled electrochemical thermal modelling of a novel Li-ion battery pack thermal management system [J]. Applied Energy, 2016, 181: 1-13.
[16] 程昀, 李劼, 贾明, 等. 锂离子电池多尺度数值模型的应用现状及发展前景 [J]. 物理学报, 2015, 64 (21): 137-152. CHENG Y, LI J, JIA M,. Application status and future of multi-scale numerical models for lithium ion battery [J]. Acta Physica Sinica, 2015, 64 (21): 137-152.
[17] WANG T, TSENG K J, ZHAO J Y,. Thermal investigation of lithium-ion battery module with different cell arrangement structures and forced air-cooling strategies [J]. Applied Energy, 2014, 134: 229-238.
[18] VERBRUGGE M W. Primary current distribution in a thin-film battery. Application to power-density calculations for lithium batteries [J]. Journal of Electrostatics, 1995, 34 (1): 61-85.
[19] DEES D W, BATTAGLIA V S, BELANGER A. Electrochemical modeling of lithium polymer batteries [J]. Journal of Power Sources, 2002, 110 (2): 310-320.
[20] FANG W F, KWON O J, WANG C Y. Electrochemical-thermal modeling of automotive Li-ion batteries and experimental validation using a three-electrode cell [J]. International Journal of Energy Research, 2010, 34 (2): 107-115.
[21] SOMASUNDARAM K, BIRGERSSON E, MUJUMDAR A S. Thermal-electrochemical model for passive thermal management of a spiral-wound lithium-ion battery [J]. Journal of Power Sources, 2012, 203: 84-96.
[22] BERNARDI D. A general energy balance for battery systems [J]. Journal of The Electrochemical Society, 1985, 132 (1): 5.
[23] AL HALLAJ S, MALEKI H, HONG J S,. Thermal modeling and design considerations of lithium-ion batteries [J]. Journal of Power Sources, 1999, 83 (1): 1-8.
[24] 李腾, 林成涛, 陈全世. 锂离子电池热模型研究进展 [J]. 电源技术, 2009, 33 (10): 927-932. LI T, LIN C T, CHEN Q S. Research development on lithium-ion battery thermal model [J]. Chinese Journal of Power Sources, 2009, 33 (10): 927-932.
[25] CHO Y I, FRANK H, HALPERT G. Computer simulation of thermal modeling of primary lithium cells [J]. Journal of Power Sources, 1987, 21 (3/4): 183-194.
[26] GU W B, WANG C Y. Thermal-electrochemical modeling of battery systems [J]. Journal of the Electrochemical Society, 2000, 147 (8): 2910-2922.
[27] CHEN S C, WANG Y Y, WAN C C. Thermal analysis of spirally wound lithium batteries [J]. Journal of the Electrochemical Society, 2006, 153 (4): A637-A648.
[28] SRINIVASAN V, WANG C Y. Analysis of electrochemical and thermal behavior of Li-ion cells [J]. Journal of the Electrochemical Society, 2003, 150 (1): A98.
[29] FAN L W, KHODADADI J M, PESARAN A A. A parametric study on thermal management of an air-cooled lithium-ion battery module for plug-in hybrid electric vehicles [J]. Journal of Power Sources, 2013, 238: 301-312.
[30] JEON D H, BAEK S M. Thermal modeling of cylindrical lithium ion battery during discharge cycle [J]. Energy Conversion and Management, 2011, 52 (8/9): 2973-2981.
[31] CHEN M, SUN Q J, LI Y Q,. A thermal runaway simulation on a lithium titanate battery and the battery module [J]. Energies, 2015, 8 (1): 490-500.
[32] 彭鹏, 孙忆琼, 蒋方明. 钴酸锂电池烤箱热滥用模拟及热行为分析 [J]. 化工学报, 2014, 65 (2): 647-657. PENG P, SUN Y Q, JIANG F M. Numerical simulations and thermal behavior analysis for oven thermal abusing of LiCoO2lithium-ion battery [J]. CIESC Journal, 2014, 65 (2): 647-657.
[33] CHEN S C, WAN C C, WANG Y Y. Thermal analysis of lithium-ion batteries [J]. Journal of Power Sources, 2005, 140 (1): 111-124.
[34] SAW L H, YE Y H, TAY A A O. Electrochemical-thermal analysis of 18650 lithium iron phosphate cell [J]. Energy Conversion and Management, 2013, 75: 162-174.
[35] REYNIER Y F, YAZAMI R, FULTZ B. Thermodynamics of lithium intercalation into graphites and disordered carbons [J]. Journal of the Electrochemical Society, 2004, 151 (3): A422.
[36] WILLIFORD R E, VISWANATHAN V V, ZHANG J G. Effects of entropy changes in anodes and cathodes on the thermal behavior of lithium ion batteries [J]. Journal of Power Sources, 2009, 189 (1): 101-107.
[37] JIANG F M, OLIVEIRA M S A, SOUSA A C M. Mesoscale SPH modeling of fluid flow in isotropic porous media [J]. Computer Physics Communications, 2007, 176: 471-480.
Thermal modeling of cylindrical lithium-ion battery module with micro-channel liquid cooling
ZHAO Chunrong1,2, CAO Wenjiong1, DONG Ti1,2,JIANG Fangming1
(1Laboratory of Advanced Energy Systems,Guangdong Key Laboratory of New and Renewable Energy Research and Development,CASKey Laboratory of Renewable Energy,Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences,Guangzhou 510640, Guangdong, China;2University of Chinese Academy of Sciences, Beijing 100049, China)
Considering the micro-channel liquid cooling thermal management system (TMS) of EV battery packs, a thermal model was established for a battery module consisting of 71 sections 18650 lithium-ion batteries. In this model, the thermal-lumped treatment was implemented for each single battery and the heat generation of a single battery was determined based on experimental measurements. In particular, heat conduction between neighboring batteries was considered. The battery module’s thermal behavior, and investigated effects of the discharge C-rate, the liquid flow rate, the heat exchange area between neighboring batteries, and the interfacing area of the battery and the shell of micro-channel were numerically studied relying on the developed model. The simulated results corroborated the effectiveness of the micro-channel cooling system. It was found that: 1) increasing the discharge C-rate led to higher temperature and worsened the temperature uniformity in the battery module; 2) increasing the liquid flow rate can significantly lower the maximum temperature and improve the temperature uniformity in the battery module; 3) increasing the exchange area between neighboring batteries slightly improved the temperature uniformity in the battery module, but only had limited effect at lowering the maximum temperature in the module; 4) increasing the interfacing area of the battery and the shell of micro-channel can significantly lower the maximum temperature in the battery module, but worsen the temperature uniformity in the module.
lithium-ion battery; thermal model; microchannels; computer simulation; heat transfer
10.11949/j.issn.0438-1157.20170278
TM 912.9
A
0438—1157(2017)08—3232—10
蒋方明。第一作者:赵春荣(1990—),男,硕士研究生。
广东省自然科学基金-重大基础研究培育(2015A030308019);广东省自然科学基金项目(2016A030313172);广东省新能源和可再生能源研究开发与应用重点实验室基金项目(Y607jg1001);中国科学院“百人计划”项目(FJ)。
2017-03-22收到初稿,2017-04-17收到修改稿。
2017-03-22.
Prof.JIANG Fangming, jiangfm@ms.giec.ac.cn
supported by the Key Scientific Development Project of Guangdong Province (2015A030308019), the Natural Science Foundation of Guangdong Province (2016A030313172), the Guangdong Key Laboratory of New and Renewable Energy Research and Development Fund (Y607jg1001) and the CAS “100 Talents” Program (FJ).
