另辟蹊径，巧解题——六年级复杂应用题教学谈

江苏省南京栖霞区迈皋桥中心小学 汪元贵

另辟蹊径，巧解题
——六年级复杂应用题教学谈

江苏省南京栖霞区迈皋桥中心小学 汪元贵

孩子到了六年级，往往会对一些复杂的应用题感到无从下手，确实，一些题如果按照正常的思维很难把它解出来，即便是老师也是如此，有时虽然能解出来，但怎么讲解能让孩子听得浅显易懂，这可就不是一件小事了。这些较复杂的应用题的解法，经过多次研究发现换个角度去思考就简单容易多了，现在把它们呈现出来，希望与大家共勉。

一、行程问题

例1 甲、乙两车分别从A、B两地同时相对开出，经过3小时相遇。两车分别到达A、B两地后，各休息1小时，再往回开。已知两车在行驶过程中速度不变，求从原地出发到第二次相遇，共需要多少小时？

分析与解答：

像这样的题，大多数学生读题后都会采用列方程的策略来解决，殊不知这条路想走通是很麻烦的。我们不妨换个思路来解决，因为已知两车在行驶过程中速度不变，两车在整个过程中相遇了两次，但对于所走的总路程来说，两车共走了三个单程，一个单程需要3小时，三个单程就要3×3=9小时，再加上休息的1小时，故而在全程中共需要3×3+1=10（小时）。

例2 A、B两地相距3200米，甲、乙两人分别从两地相对而行，甲每分钟行82米，乙每分钟行78米，甲带着一条狗一起出发，狗每分钟跑330米，当狗遇到乙时，转身向甲方向跑，遇到甲时再转身往乙方向跑，如此往返，当甲、乙两人相遇时，这条狗共跑了多少米？

分析与解答：这是一道比较经典的思维拓展题，单从小狗跑来跑去，就让你丈二和尚——摸不着头脑，可不是吗？如果一段一段地求出小狗跑的距离，似乎是不可能的事。这时我们可以换个角度考虑，小狗在两人相遇时也就停止了跑动，由此可见，小狗所跑的时间就是两人相遇的时间，即3200÷（82+78）=20（分钟），狗每分钟跑330米，当甲、乙两人相遇时，狗一共跑了330×20=6600（米）。

二、复杂的分数问题

例3 三人合买一栋别墅。老大出资50万元，老二出资额是另外两个兄弟总额的1/2，老三出资额是另外两个兄弟总额的1/3。这栋别墅售价多少万元？

分析与解答：单从文字叙述来看，这道题并不复杂，但是要让学生真正理解它，真的不容易，由于1/2和1/3的单位“1”不同，给问题的解决带来了不小的麻烦。我们能否把两个分数的单位“1”统一成一样呢？在孩子的共同参与下，我豁然开朗，决定用线段图来完成，方法如下：

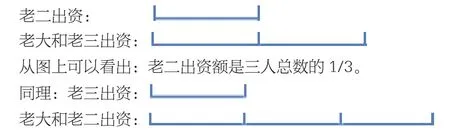
老三出资额是三人总数的1/4。

这样老二和老三出资额都是以三人出资总额为单位“1”的，故老大的出资额就是总数的1－（1/3+1/4）=5/12,50÷5/12=120（万元），问题得以解决。

例4 某电厂原有职工160人，其中女职工占11/20，后来调走了一批女职工，这时女职工占总人数的5/11。现在这个电厂有多少女职工？

分析与解答：本题中电厂总人数和女职工人数都在变化，但男职工人数始终没变，解答这道题的关键就是抓住这个不变量来解决。先求出男职工人数：160×（1－11/20）＝72（人）。调走了一批女职工后，这时男职工占总人数的（1－5/11），这样就可以求出一批女职工调出后电厂的总人数为72÷6/11＝132（人）。那么，现有女职工人数是：132×5/11＝60（人）。

例5 学校田径队女生人数原来占总人数的1/3，后来有6名女生加入，这样女生人数就占田径队总人数的4/9。现在田径队有女生多少人？

分析与解答：这道题乍一看很好理解，1/3和4/9的单位“1”都是田径队的总人数，于是大部分学生采用6÷（4/9－1/3）=54(人)，认为这是田径队的总人数，现在女生有54×4/9=24（人）。但仔细一分析，你会发现，虽然它们的单位“1”都是田径队总人数，但“4/9”对应的总人数是加入6名女生后的总人数，它们是不同的总人数，因此上述解法是错误的。本题的解法依然和例5的解法一样，找出题中的不变量——男生人数为突破口，把所给信息换个说法，“女生人数原来占总人数的1/3”可以换成“女生人数是男生人数的1/2”，同样，“女生人数就占田径队总人数的4/9”可以换成“女生人数是男生人数的4/5”，这样就把单位“1”统一成了不变的量——男生人数，问题便迎刃而解。先求男生人数6÷（4/5－1/2）=20（人），再求现在的总人数20÷（1－4/9）=36(人)，则现在的女生有36－20=16（人）。

例6 民族小学合唱队中，六（5）班合唱人数是六（1）班合唱人数的2/3，从六（1）班合唱队调8个人到六（5）班合唱队后，六（1）班的合唱人数是六（5）班的5/6。这两个班合唱队一共有多少人？

分析与解答：在这道题中有两个单位“1”，而这两个单位“1”对应的总数在调8人后都发生了变化，所以单从这方面考虑去解决这个问题，就会钻进一个死胡同。不妨这样想：无论两个合唱队的人数怎样调动，这两个班合唱队的总人数都是没有变化的，抓住这一点，我们将2/3和5/6的单位“1”统一成两个班合唱队的总人数，未调学生之前，由六（5）班人数是六（1）班人数的2/3可得原来六（5）班合唱人数占两班合唱队总人数的2/5，学生调动之后，由六（1）班的人数是六（5）班的5/6可得现在六（5）班合唱队人数是两个班合唱队总人数的6/11。六（5）班合唱队人数由原来占两班合唱队总人数的2/5变成6/11，正是因为从六（1）班调入8人所致，因此，两个班合唱队总人数是8÷（6/11－2/5）=8÷8/55=55（人）。

从例4、例5、例6中可以看出，无论是调出、调进还是从一个量调入另一个量，我们只要抓住一个不变的量，问题就会顺利解决。