基于Curvelet的指纹纹理识别算法

王植

（西安航空职业技术学院 陕西 西安710089）

基于Curvelet的指纹纹理识别算法

王植

（西安航空职业技术学院 陕西 西安710089）

近年来，Curvelet变换由于其独特性而受到研究人员的日益关注。Curvelet变换是各向异性的，具有很强的方向性，非常有利于图像边缘的高效表示；它是一种多分辨，带通，具有方向性的函数分析方法，鉴于Curvelet的这些优良特性，本文提出了把指纹图像看成有方向和频率的纹理信号，利用Curvelet有频率和方向选择的特性，对指纹纹理图像进行Curvelet滤波，得到指纹图像的局部纹理特征图；然后对局部特征图进行编码，计算编码间的距离。该方法充分利用了蕴含在指纹灰度图像中的丰富纹理信息，又反映了指纹的局部信息，弥补了传统方法对小面积指纹图像识别上的不足且具有很强的抗干扰能力，有较高的实用价值。

指纹识别；Curvelet变换；Curvelet滤波；纹理特征

随着社会和经济的发展，人们对身份鉴别的准确性，安全性与实用性提出了更高的要求。基于信物或口令的传统身份鉴别方式存在容易丢失，遗忘，被复制及盗用的隐患。通过辨别人的生理和行为特征进行身份认证的生物识别技术提供了一个方便可靠的解决方案。伴随着计算机图形图像处理技术和模式识别技术的发展，指纹自动识别技术也有了突破性发展。

1 Curvelet变换

1999年Cand`es和Donoho提出了Curvelet变换理论，Curvelet变换是各向异性的，具有很强的方向性[4]，非常有利于图像边缘的高效表示。后来，Cand`es等人于2002年提出了新的Curvelet框架体系，称之为第二代Curvelet变换。新的理论框架结构为提高Curvelet变换实现速度提供了可能。在此之后，他们又于2005年提出了两种基于第二代Curvelet变换理论的快速离散实现方法[5]。和小波变换、脊波变换理论一样都属于稀疏理论的范畴之内，采用基函数与信号（或函数）的内积形式实现信号（或函数）的稀疏表示，从而Curvelet变换可表示为[4]：

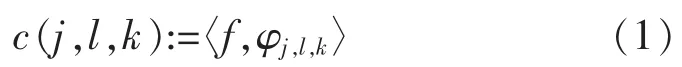
其中，φj，l，k表示 Curvelet函数，j，l，k 是分别表示尺度，方向，位置参量。

Curvelet变换在频域内实现，采用频域中的窗函数U来实现φ在频域中的表示。

定义一对窗函数：径向窗函数 W（r），r∈（1/2，2）和角度窗函数 V（t），t∈[-1，1]，它们都满足可允许条件，

对于每一个j≥j0，在频域中定义频窗Uj如下，

其中⎿j/2」是j/2的整数部分。Uj的支撑区间是受W和V支撑区间限制获得的楔形区域。楔形区域符合各向异性尺度的特性。令。j尺度上的φj表示知道了，其他2-j尺度上的Curvelet均可由φj通过旋转和平移获得。定义：

1） 均匀的旋转角度序列：θl=2π·2-⎿j/2」·l，l=0，1，…，0≤θl＜2π

2） 平移参数：k=（k1，k2）∈Z2

综合以上概念，定义在尺度2-j，方向 θl，平移参数（k1，k2）处的 Curvelet为

2 对指纹图像做Curvelet滤波

把事先经过预处理的256×256大小的指纹图像进行4层Curvelet正变换，将得到分别属于1个Coarse层，2个Detail层和1个Fine层的Curvelet系数。由于指纹的纹理信息大部分都集中在Detail2层，如图1所示 ，把一副加噪声的指纹图像经过Curvelet变换后得到的Detail2层系数图像有效的保留了原来的指纹信息，滤除了噪声。

图1 原始图像，加噪图像以及Curvelet变换后的各层系数图像

所以将其他层的系数全部置为0，只保留Detail2层的系数。Detail2层包含了32个角度方位，每个角度方位包含一个系数矩阵。把这32个角度方位按照对角线（如图2所示）分成4个大方位，这样每个大方位中包含8个小方位。

图2 Detail2层32个角度方位阵分布图

由于一，三方位的系数矩阵所表示的指纹图一样，二，四方位的系数矩阵所表示的指纹图一样，所以我们只选取一，二方位来做处理，而把三，四方位的系数矩阵全部置0。我们把一，二方位中的16个小方位按每2个小方位为一个方向的规则进行划分，这样将得到0到之间的8个方位角度。最后再对所有系数进行Curvelet逆变换，经过Curvelet滤波后我们就得到了8个方向上的指纹局部纹理特征图，如图3所示。

经过Curvelet滤波后的指纹图像较好的去除了噪声，增强了兴趣方向的信息，保留了真正的脊谷结构。

3 指纹图像的编码与匹配

本论文将采用Jain等人的方法[6-10]，把得到的这8个方向的局部纹理特征图均分成3×12份的圆形网格，如图所示。

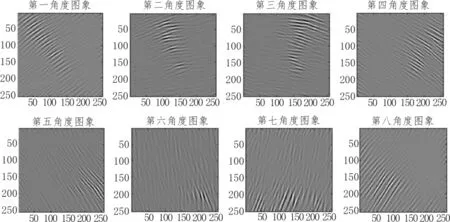
图3 0-π方向的指纹局部纹理图

把每幅指纹局部信息，以指纹中心点确定的基准点为圆心，分为38个区域：其中1-12区半径12＜R＜32，隔π/6沿逆时针方向依次排列；13-24区半径32＜R＜52，隔π/6沿逆时针方向依次排列；25-36区半径52＜R＜72，隔π/6沿逆时针方向依次排列；半径R＜12的区域为37区；半径R＞72的图像区域为38区。其中每隔π/6划分一个区域，计算该区域的均值统计后，可以提高指纹识别系统的旋转不变性。

圆形分区将指纹局部纹理特征图像分区后，以区为单位建立特征编码。Jain等人用子块的绝对平均偏差值或者平均平方偏差值作为其特征，收到良好的效果。本文将选用扇格块的平均绝对偏差值[11]作为特征。

扇格块的平均绝对偏差值是扇格块内每一点灰度值与扇格块内平均灰度值之间的绝对偏差的平均值，它反映了扇格块间脊线的差异。定义为：

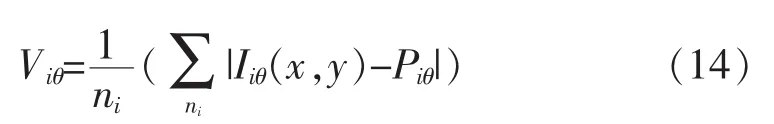
其中，Iiθ（x，y）为 θ方向滤波后指纹图像的 Si扇格块内像素（x，y）的灰度值，Viθ为平均绝对偏差值。i为扇格的个数，θ为方向，ni为扇格Si内的像素总数，Piθ为扇格内像素的灰度均值。

4 实验结果

衡量指纹识别算法性能最重要的两个指标是认假率（False Acceptance Rate，FAR） 和拒真率（False Reject Rate，FRR）。FAR 和 FRR 是成反比的，设定不同的距离阈值，FAR和FRR也是不同的。距离值增大，说明系统更强调易用性，因而FRR降低，FAR增大；相反，距离阈值减小说明系统更强调安全性，因而FAR降低，FRR增大。

我们在PC机上实现了该算法，并随机抽取了256×256大小分辨率为500DPI的81枚已在指纹库中的指纹和18枚不在指纹库中的指纹进行比对结果如表 1，2。

表1 81枚指纹数据表

表2 18枚指纹数据表

文中算法和Gabor滤波算法的比对结果如下：

表3 文中算法和Gabor滤波算法对比

试验结果表明本文算法比Gabor滤波算法的匹配性能有所提高。

为了追求其安全程度，我们所设阈值较低，而且指纹采集时，手指按压的力度和角度的不同以及手指轻微的颤抖，移动等均导致采集的指纹图像差异较大，这样可能影响一定的识别率。

5 结束语

Curvelet变换以边缘为基本表示元素，具有完备性，能很好的适合图像的特点。另外，Curvelet变换是各向异性的，具有很强的方向性。虽然Curvelet变换诞生的时间不长，对它的研究还远不如小波成熟，但是由于其崭新的理论面貌和独到的应用特点，已经得到了相关研究人员的高度重视，也取得了相当多的研究成果，其中Curvelet应用于指纹识别就是一个全新的尝试。实验效果证明，该算法能够满足实际指纹识别的需要。

[1]黄薇.Curvelet变换及其在图像处理中的应用研究[D].西安：西安理工大学，2007.

[2]Candes E J，Demanet L，Donoho D L.Fast Discrete curvelet transform[R].Applied and Computational Mathematics，California Institude of Technology.2005：1-43.

[3]Jain A K，Duta N.Deformable matching of hand shapes for verification[J].Proceedings of IEEE ICIP，1999（9）：1124-1136.

[4]Jain A K，et al.Biometrics：Promising frontiers for emerging identification market[J].Communication ACM，2000（2）：91-98.

[5]Jain A，Hong L，Pankanti S.An identity authentication system using fingerprints[J].Proceedings of.IEEE，1997，85（9）：1365-1388.

[6]Jain A，et al.On-line fingerprint verification[J].IEEE Transactions on PAMI，1997，19（4）：302-314.

[7]赵振磊，耿则勋，张亚新，等.基于第二代Curvelet变换的自适应图像增强 [J].计算机工程与应用，2009（9）：192-195.

[8]杨居义.基于第2代Curvelet变换的彩色图像去噪[J].计算机工程，2010（5）：207-209.

[9]刘涛，张登福，何宜宝.基于区域分割和非下采样Contourlet变换的多聚焦图像融合算法[J].计算机应用，2010（10）：2805-2807.

[10]李逵，狄红卫.一种基于二代Curvelet变换的图像融合新算法[J].暨南大学学报：自然科学与医学版，2008（1）：11-15.

Curvelet-based fingerprint texture identification algorithm

WANG Zhi
（Xi’an Aeronautical Polytechnic Institute，Xi’an 710089，China）

In recent years，Curvelet transform because of its unique the researchers have been increasingly concerned about.Curvelet transform is anisotropic，and are highly directional，very much in favor of high-performance edge，said.It is a multi-resolution，band-pass，with a directional analysis function.In view of the Curvelet of these fine features，this paper，the fingerprint image as the direction and frequency of the signal texture，use a Curvelet frequency and direction of the selected features，fingerprints of Curvelet image texture filtering，so we can obtained the local texture characteristics graph.And then to the local characteristics graph，calculating the distance between the codes.This method makes full use of fingerprints contained in the gray image of rich texture，and reflects the partial fingerprint information，to make up for the traditional method of fingerprint image identification small area on the less and has a strong anti-interference ability，high the practical value.

fingerprint recognition；Curvelet transform；Curvelet smoothing；texture feature

TP391.4

：A

：1674－6236（2017）13-0068-04

2016-05-25稿件编号：201605240

王 植（1983—），男，陕西凤翔人，硕士，讲师。研究方向：信息处理，数据挖掘。