激光扫描糙米三维可视化数字建模

孔祥亮 汤晓华 吴星宇郑龙安 郝方涛 安嘉强

(1. 北京工商大学材料与机械工程学院，北京 100048；2. 北京邮电大学自动化学院，北京 100876)



激光扫描糙米三维可视化数字建模

孔祥亮1汤晓华1吴星宇2郑龙安1郝方涛1安嘉强1

(1. 北京工商大学材料与机械工程学院，北京 100048；2. 北京邮电大学自动化学院，北京 100876)

糙米建模是深入研究碾白加工的基础。以离散断层截面环形扫描组合搭建原理为基础，高精度激光位移传感器为检测仪器，设计开发糙米数字化检测装置，实现糙米离散截面的非接触数字化测量。针对原始测量数据的特点进行了滑动平均滤波及椭圆拟合处理，并对处理前后的数据进行了误差对比分析。建模过程结合逆向工程领域的基本理论探讨了糙米三维可视化数字建模方法，构建基于椭圆参数和经纬包络描述的糙米数字化模型，可为研究糙米加工提供有效参考。

糙米建模；断层截面环形扫描；激光位移传感器；非接触数字化测量

大米加工产业在中国的国计民生中一直占有举足轻重的地位，随着社会经济的发展和市场需求的变化，如何将目前中国大米加工领域中的“精制碾米”转化为更营养、健康的“留胚碾米”，成为粮食加工领域急需探索的课题之一[1]。

糙米中60%以上的营养元素都积聚在占糙米重量10%的糠层和胚芽中，因此胚芽米的营养价值远高于普通大米[2]。为实现大米加工产业中的“精制碾米”向“留胚碾米”转型，碾白加工过程中糙米糠层去除及留胚机理成为研究分析的关键所在。建立较为精确的糙米数字化模型，可为分析糙米在胚芽米碾白室内的运动过程提供精确的计算依据。此外，通过分别建立糙米模型与精米模型,并对两者进行对比，可对胚芽米加工的最小加工量及出米率等参数进行分析，从而为研究新型的胚芽米加工工艺奠定基础。因此，研究建立较为精确的糙米数字化模型具有理论意义及应用价值。

合理选择数据测量仪器是实现糙米精确数字化建模的基础前提，目前市场上常用的数字化设备主要包括结构光测量仪、三维扫描仪等产品，其特点及应用范围各有不同。由于糙米籽粒较小且形状不规则，现有设备难以实现对其表面数据的精确采集。本试验以KEYENCE LK-G150感测头、KEYENCE LK-GD500控制器作为核心部件，设计开发了一套高精度的糙米数字化检测装置，并结合逆向工程领域的基本理论，探讨了糙米三维可视化建模方法。

1 检测系统设计及开发

1.1 检测原理及装置开发

糙米轮廓检测采用离散截面扫描原理。糙米轮廓呈近似长扁椭圆形。通过沿糙米长轴方向多截面环形扫描获得其各截面散点数据，当截面数足够时，将扫描点云数据拼接即可获得糙米轮廓。

为实现糙米表面数据的全方位采集，开发糙米扫描设备见图1。其中测量装置需满足如下功能：① 激光位移传感器能够沿OXYZ坐标系3个坐标轴方向移动；② 被测物(即糙米)能够绕X'轴转动。图1中1、2、3、5构成激光位移传感器检测部装，其中5为激光位移传感器，用于检测被测物的位移；部件1驱动Z轴方向丝杠旋转，用于调整传感器激光射线与糙米回转中心线等高，调整好后即锁紧；部件2驱动Y轴方向丝杠旋转，用于调整传感器测量范围，聚焦调整好后即锁紧；部件3驱动X轴方向丝杠旋转，实现糙米沿X轴方向间歇环扫功能。X、Y、Z轴丝杠旋转分辨率均达到0.01 mm，可满足精确调节数据检测时所需的进给距离。4、6构成糙米环形扫描检测部装，其中部装4实现精确分度、带动糙米间歇回转运动(Δωx')。

1.Z轴丝杠传动系统(实现传感器高度位置调节) 2.Y轴丝杠传动系统(实现糙米与传感器相对位置调节) 3.X轴丝杠传动系统(实现沿糙米长度方向进给) 4. 分度盘(实现环形分度扫描) 5. 激光位移传感器 6. 糙米

图1 糙米表面数据检测装置原理图

Figure 1 Schematic diagram of surface data detecting device for brown rice

1.2 传感器原理分析

激光位移传感器是一种基于激光三角法的非接触式精密激光测量系统[3-5]，其原理是：用一束激光以某一角度聚焦在被测物体表面，然后从另一角度对物体表面上的激光光斑进行成像，物体表面激光照射点的位置不同，所接受散射或反射光线的角度也不同，用CCD或PSD(位敏探测器)测出光斑像的位置，即可计算出物体表面激光照射点的位置。当物体沿激光线方向发生移动时，测量结果就将发生改变，从而实现用激光测量物体的位移[6-7]。其测量原理见图2。

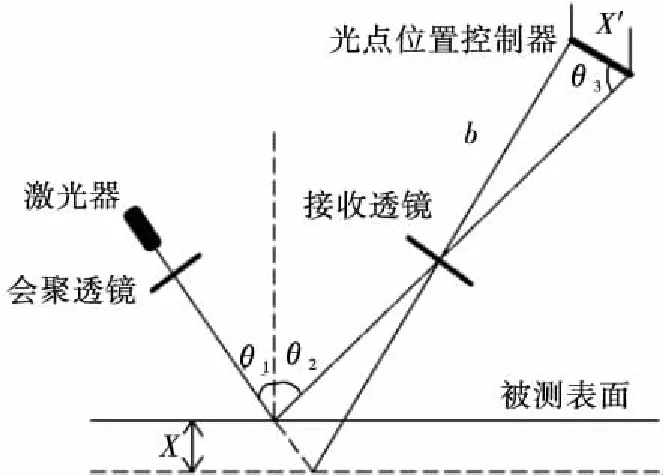
图2 激光位移传感器测量原理

1.3 传感器选择

根据研究对象的特点及仪器性能选择KEYENCE LK-G150感测头、KEYENCE LK-GD500控制器作为测量装置的核心部件。此传感器使用CCD作为光接收原件，CCD检测每个像素上光点的光量分布峰值并将此确定为目标物位置，因此CCD能够提供稳定的高精度位移测量，而不考虑光点光量分布状况。

KEYENCELK-G150感测头可检测不透明或半透明材料，在漫反射模式下进行测量的参考距离为150 mm，在镜面反射模式下进行测量的参考距离为147.5 mm，参考距离下光点直径约120 μm，再现性达0.1 μm，重复精度达0.5 μm，采样周期可在等级20，50，100，200，1 000 μs中选择，其性能完全满足测量要求。

2 糙米表面数据采集

数据采集系统主要实现获取被测物糙米表面的三维点云信息。测量点的分布和数量直接影响曲面重建的方法和效果[8]。因此，在实施扫描前制定合理的扫描方案对于后续的模型构建至关重要。

糙米模型近似于扁椭球体，因此可将糙米看成回转体，将糙米固定在分度盘中心轴顶端，使其长轴与图1检测装置X方向一致。用高精度激光位移传感器间隔一定的轴向距离扫描糙米截面轮廓，并将每个截面细分为360°，每度设置一个测量点，对各测量点采集100个数据,并求其均值用于描述该点，由此可实现糙米表面数据的全方位精确测量。

依据KEYENCE LK-G150感测头使用说明书完成相关硬件安装及LK-Navigator数据采集系统软件安装调试。运行环境符合其使用要求。其中KEYENCE LK-G150感测头对被测物材质和反射方式敏感。糙米主要成分为淀粉，因此本研究将测量模式设置为“半透明”；反射方式设置为“漫反射”。其测量流程见图3。按照图3流程完成完整糙米点云数据采集、保存。

图3 测量流程图

3 糙米表面数据处理

3.1 测量数据分析

为检验传感器测量模式选择的正确性及测量精度，此处以第13个截面上0～2°检测点各100个测量数据为例进行数据质量分析，由表1可知，传感器工作状态稳定，测量数据波动范围在±0.5 μm之内，可实现糙米表面数据的高精度测量。

表1 第13截面部分测量数据分析

3.2 测量数据前处理

激光位移传感器的测量结果为被测物(即糙米)相对于参照物的位移值。本试验选择直径为4 mm的光轴作为参照物，当传感器激光射线调整至与该参照物轴线处于同一水平面时，将传感器显示数值清零，此后将糙米表面各点测量数据按式(1)计算，得到糙米截面上各点对应的极径。

ρ=R+Δ，

(1)

式中：

ρ——极径，mm；

R——参照物半径，2 mm；

Δ——测量值，mm。

表2为糙米第13截面上0～5°所对应的测量数据及其极径。

3.3 测量数据图形显示

MATLAB作为功能强大的数学软件，集数据分析、数值计算、算法开发及数据可视化等功能于一体，具有完备的图形处理显示功能，可实现计算结果和编程的可视化[9]，故本研究采用MATLAB对测量点云数据进行分析处理及图形显示。

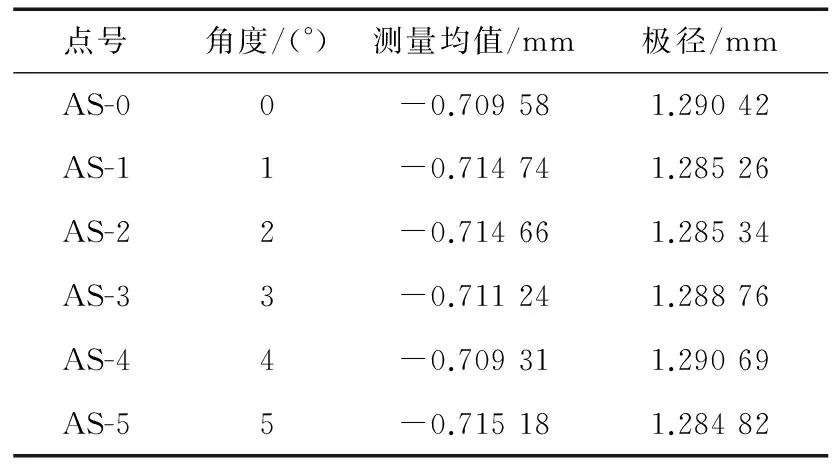
表2 第13截面部分测量数据及其极径

首先按点读取糙米各截面扫描数据，在此基础上进行数据组合并加以显示。在MATLAB中选用textscan函数循环读取各截面的测量数据。由于测量时对各截面中的每个点均采集100个数据，因此对读入的每个点的数据用mean函数求均值，并将均值分别存入3个行矩阵M1×10，N1×90，P1×260中，形成各截面的点描述数据矩阵。其中M1×10存放每个截面中0～9°对应的10个点数据，N1×90存放10～99°对应的90个点数据，P1×260存放100～359°对应的260个点数据。合并3个行矩阵得到截面点描述数据矩阵A=[M,N,P]，对矩阵A中的数据按式(1)计算,可得到糙米截面上所有点对应的极径，由每个点所对应的极径和角度，即可使用Polar命令在极坐标系下绘制糙米截面轮廓图。第13～22个截面的程序运行结果见图4。

3.4 数据后处理及误差分析

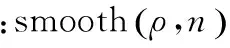
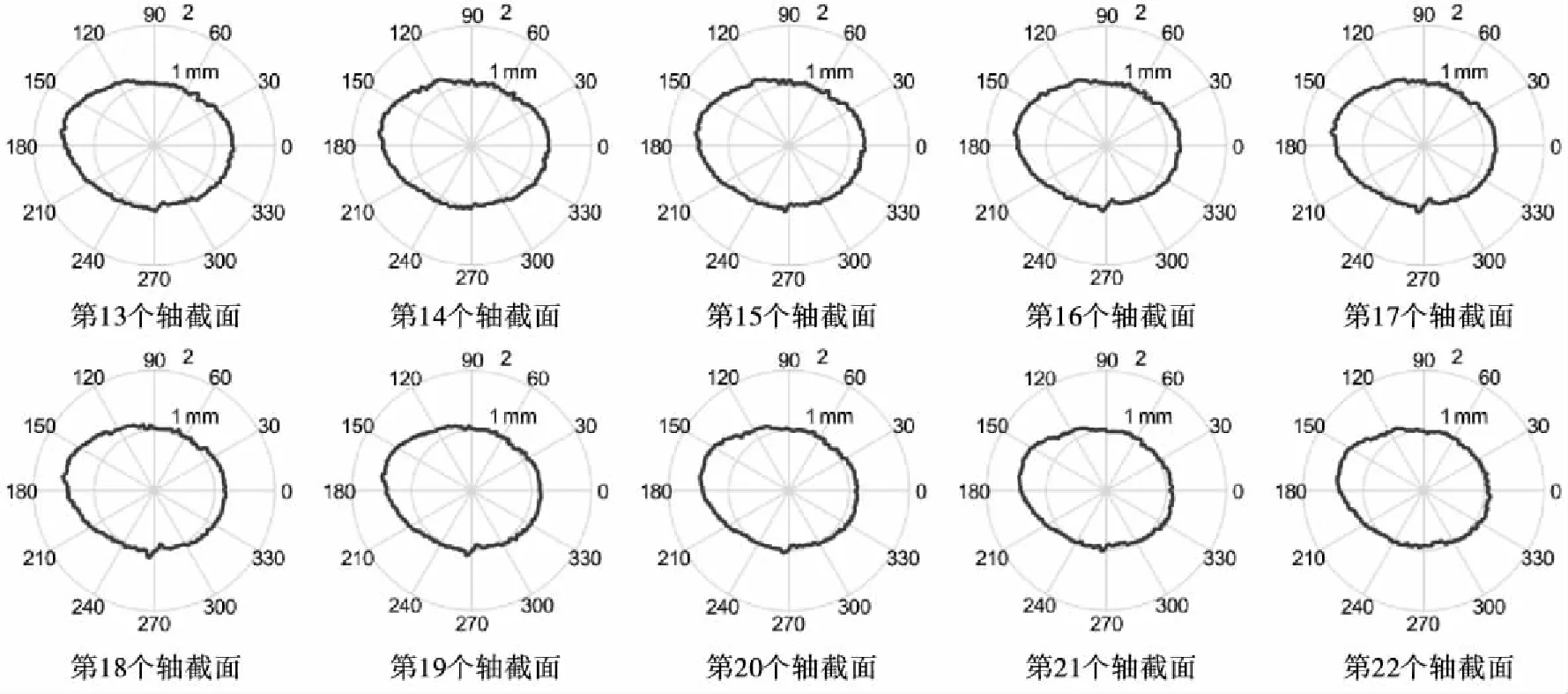
图4 糙米部分截面轮廓

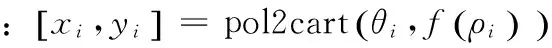
3.4.2 糙米截面椭圆拟合 根据3.3可知糙米多数截面轮廓形状近似于椭圆，为实现对其进行明确的函数表示，以方便对糙米截面的长短轴尺寸等特征进行定量分析，本研究采用最小二乘法对形状近似于椭圆的截面轮廓进行椭圆拟合。

最小二乘拟合是最早的椭圆拟合方法，其思想为考虑数据受随机噪声的影响进而追求整体误差的最小化[11]。设椭圆的隐式方程F=(a·x)=0，其中a=(A,B,C,D,E,F)为椭圆方程的系数，将误差距离定义为隐式方程在给定离散点与拟合点之间的偏差，取椭圆隐式方程为：

F(x,y)=Ax2+2Bxy+Cy2+Dx+Ey+F=0。

(2)

将测量值(xi,yi),i=1,2,……,k代入椭圆隐式方程时，因存在误差，F(xi,yi)一般不等于0，认为F(xi,yi)是点(xi,yi)到拟合椭圆的代数距离，由此可通过使给定离散点与拟合椭圆的代数距离平方和为最小来求椭圆隐式方程系数[12]。

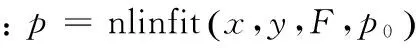
此处以第14、25截面数据为例，滤波前后的椭圆拟合程序运行结果见图5。

表3、4分别列出了上述两典型截面数据滤波前后椭圆拟合误差及椭圆方程系数对比结果。由表3可知，第14个截面数据滤波前后最大拟合误差点的误差值分别占该点对应椭圆极径的11.05%，7.65%，误差平均值分别占椭圆半短轴的3.74%，2.96%，数据滤波前后拟合椭圆长轴相对减小了0.06%，短轴相对增大了0.01%，最大误差、误差平均值、误差方差分别相对减小了32.26%，20.88%，49.23%。第25个截面数据滤波前后最大拟合误差点的误差值分别占该点对应椭圆极径的15.23%，12.41%，误差平均值分别占椭圆半短轴的5.69%，5.12%，数据滤波前后拟合椭圆长轴相对减小了0.08%，短轴相对增大了0.02%，最大误差、误差平均值、误差方差分别相对减小了20.37%，10%，19.01%。由此可见，数据滤波效果明显，有效减小了椭圆拟合误差。

图5 数据滤波前后椭圆拟合

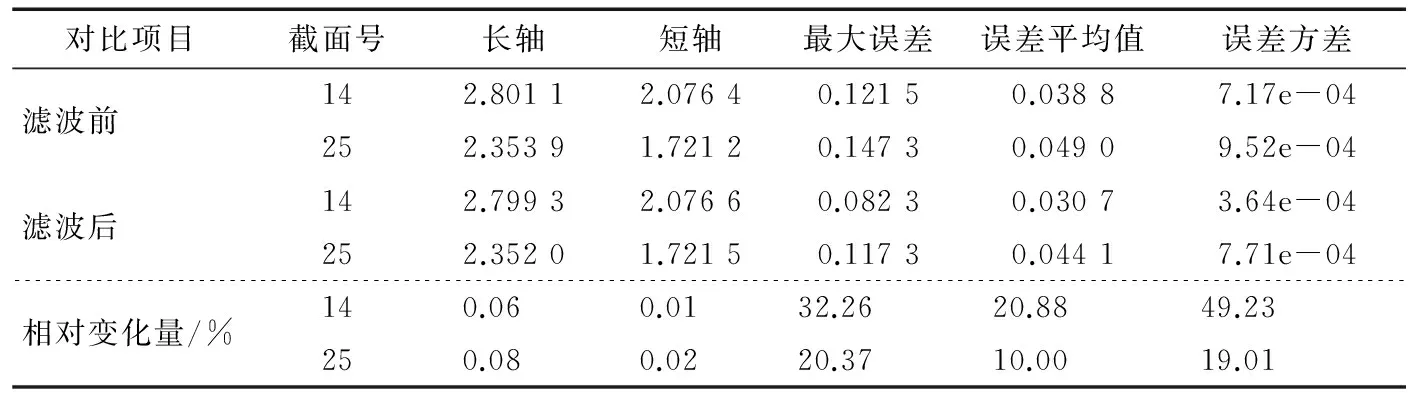
对比项目截面号长轴短轴最大误差误差平均值误差方差滤波前142.80112.07640.12150.03887.17e-04252.35391.72120.14730.04909.52e-04滤波后142.79932.07660.08230.03073.64e-04252.35201.72150.11730.04417.71e-04相对变化量/%140.06 0.01 32.26 20.88 49.23 250.080.0220.3710.0019.01

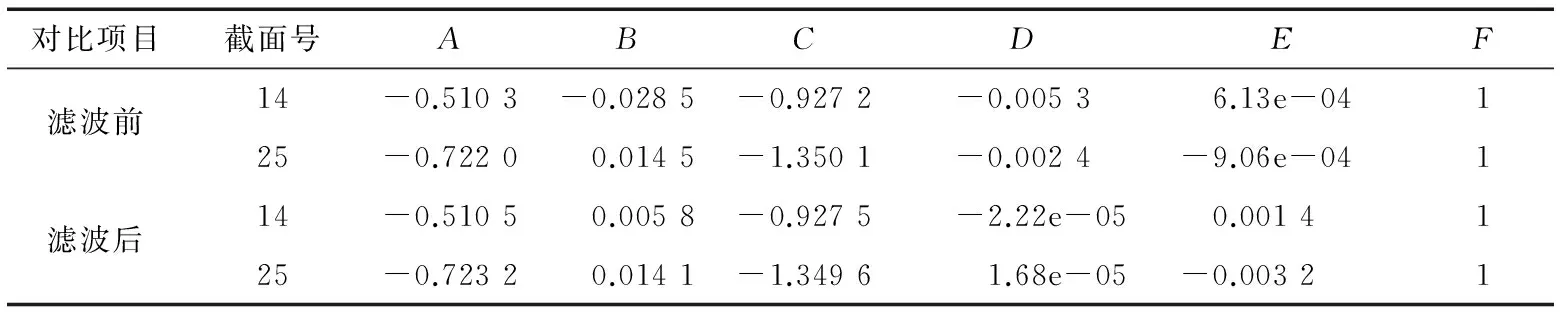
表4 数据滤波前后椭圆拟合方程系数

4 糙米表面包络线建模

将原始测量数据作滤波处理后进而绘制糙米表面经纬包络线，可以更加真实地还原糙米外观特征并为后续研究提供处理依据。经向包络线指不同截面上对应同一角度点的连线；纬向包络线指同一截面上点的连线(即截面轮廓线)。经纬线分割形成的矩形网格将对后续研究糙米外表曲面拟合具有重要意义。

绘制包络线需提供各测量点的三维直角坐标值，根据各离散截面之间的采样间隔可计算出各采样点对应的立标zi，将zi与经滤波处理后的截面数据(xi,yi)相匹配便可得到各测量点的三维直角坐标(xi,yi,zi)，再把每个截面上各测量点的三维直角坐标分量所对应的列矩阵xi=1～M(N×1)、yi=1～M(N×1)、zi=1～M(N×1)分别组合，得到3个矩阵Ex(N×M)，Ey(N×M)，Ez(N×M)，其中N为每个截面上的测量点数，M为测量截面数，Ex、Ey、Ez中第j行分别存放第1～M截面上对应同一角度点的坐标分量x、y、z。运用plot3函数即可绘制出糙米表面包络线，结果见图6。

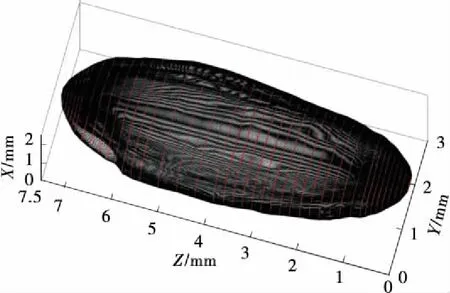
图6 糙米包络线模型

5 结论

以上分析表明，使用高精度激光位移传感器测量糙米表面坐标数据的方法可行。在数据处理及拟合后，经分析可知，可以用椭圆描述大部分糙米截面，糙米总体上呈扁椭球形。上述工作为后续建立更加精确的糙米数字化模型提供了可靠的测量手段和数据处理方法，但糙米胚芽部分凹陷处的曲率变化较大，数据采集效果有待进一步改善。构建糙米三维数字化模型可为今后研究碾白加工提供基础模型和依据。

[1] 周立汉, 薛庆林, 段笑敏, 等. 从“精制碾米”到“留胚碾米”: 大米加工产业化生产的方向[J]. 农产品加工, 2013(5): 14-16.

[2] 李维强. 大米加工技术及其开发应用[J]. 粮油食品科技, 2011(4): 8-9.

[3] 曹鹏, 尹文庆, 吴林华, 等. 基于激光传感器的稻种轮廓形状测量方法研究[J]. 传感器与微系统, 2017(3): 30-31.

[4] ROECKSEISEN Armin (DE). Method for the contact-free mea-surement of the distance of an object according to the principle of laser triangulation: US, 6088106[P]. 2000-07-11.

[5] ROECKSEISEN Armin DR (DE). Method for contactless measurement of the distance to an object using the principle of laser triangulation: EP, 0913707[P]. 1999-05-06.

[6] 朱万彬. 激光位移传感器在物体表面形状测量中的应用[J]. 光机电信息, 2010(10): 70-71.

[7] 马自军, 杨双莲. 激光位移传感器测量原理及应用研究展望[J]. 甘肃科技, 2012(2): 77-78.

[8] 张嫔. 逆向工程中散乱数据处理与模型重建技术研究[D]. 杭州: 浙江大学, 2006: 3-4.

[9] 王玉梅. MATLAB程序设计在数学建模中的应用[J]. 电子技术, 2013(9): 21-22.

[10] 黄凯明. 滑动平均数字滤波参数研究[J]. 集美大学学报: 自然科学版, 2006(4): 381-382.

[11] 马向南, 李航, 刘丽丽, 等. 最小二乘改进算法及其在椭圆拟合中的应用[J]. 河南科技大学学报: 自然科学版, 2014(3): 18-20.

[12] 夏菁. 椭圆拟合方法的比较研究[D]. 广州: 暨南大学, 2007: 4-5.

[13] 代冬岩, 李智勇, 张宏礼. 最小二乘曲线拟合及其MATLAB实现[J]. 黑龙江科技信息, 2009(21): 36.

Three-dimensional visual digital modeling of brown rice based on laser scanning

KONG Xiang-liang1TANG Xiao-hua1WU Xing-yu2ZHENGLong-an1HAOFang-tao1ANJia-qiang1

(1.BeijingTechnologyandBusinessUniversity,SchoolofMaterialsScienceandMechanicalEngineering,Beijing100048,China; 2.BeijingUniversityofPostsandTelecommunications,SchoolofAutomation,Beijing100876,China)

The modeling of brown rice is the basis of the further research on rice milling process. Based on the principle of the combined building of discrete fault annular section, by using high precision laser displacement sensor as detecting instrument, digital detecting device for brown rice was designed and developed to achieve a non-contact digital measurement of the discrete section of brown rice. Moving average filter and ellipse fitting were adopted according to the characteristics of the original measurement data, and the error analysis of data before and after treatment were compared and investigated. The modeling process was based on the basic theory of reverse engineering, and then three-dimensional visual digital modeling method of brown rice was discussed. It was found that the digital model based on ellipse parameters and the envelope of latitude and longitude could provide an effective reference for the study of brown rice processing.

brown rice modeling; fault section circular scanning; laser displacement sensor; non-contact digital measurement

孔祥亮，男，北京工商大学在读硕士研究生。

汤晓华(1963—)，男，北京工商大学教授，博士。 E-mail: tangxiaohua@th.btbu.edu.cn

2017—04—20

10.13652/j.issn.1003-5788.2017.06.017