偏最小二乘回归分类法的个人信用评估

代婷婷，单长吉，韩 艳，胡晓飞

（1.昭通学院 数学与统计学院，云南 昭通 657000；2.昭通学院 物理与电子信息工程学院，云南 昭通 657000）

偏最小二乘回归分类法的个人信用评估

代婷婷1，单长吉2，韩 艳1，胡晓飞1

（1.昭通学院 数学与统计学院，云南 昭通 657000；2.昭通学院 物理与电子信息工程学院，云南 昭通 657000）

针对目前商业银行的信用风险问题，提出了偏最小二乘回归分类法的个人信用评估算法，首先，将客户和相应的信用指标量化后做成一个矩阵；其次，建立偏最小二乘回归分类模型；最后，利用德国信用数据在该模型进行试验，得出结果。仿真结果表明，此方法简单、可行、有效。

个人信用评估 ；偏最小二乘回归分类；激活函数

随着经济的飞速发展，买房子贷款、买车子贷款、学生上学贷款，利用信用卡提前消费等等这些现象在生活中屡见不鲜，而且已经很普遍，且已经成为商业银行竞争的优势和获取利润的来源。[1]去年的一篇报道称，全国目前的各项贷款中个人贷款所占的比重已经达到了47%，而且还有持续上升的趋势，而在个人贷款中占据比例最多的是住房按揭贷款，已经在个人贷款中的比重达到了72%[2]，这种情况下，个人信用风险自然会受到极大的关注。实际上，与商业风险评估相比较，我们的个人的信用评估落后很多，一般情况下，都是依据信用机构信贷员的经验主观下结论决定。[3]这种情况只能适用于小规模的业务量。面对日益上涨的业务量，银行的信贷人员缺乏不足的情况下，这种授信方式需要很长的审批时间，在此期间有可能就会将认为的误差扩大化。相应的服务水平也会不断下降，这样会直接导致资产质量下降，潜在客风险的管控能力也提不上去，这就严重影响了银行及信用机构的竞争能力。因此，优秀的个人信用评估模型势建立显得非常有必要和紧迫，目的是快速的提高信用机构的授信效率，同时也使它的准确率尽可能的高。在此过程中，我们的个人信贷机制能够尽快的完善。风险防控的能力也逐步提高加强。

信用风险问题一直伴随存在于每一个信贷机构在开展信贷业务的过程之中，因此，它已经成为各个信贷机构预防及严格控制风险时最先要考虑的。于是，信用机构在贷款之前进行个人信用的评估显得异常重要，可是，如何在繁忙的工作中提高信用评估的效率，就需要一个科学合理的评估方法，打分制与主观经验的结合肯定是行不通的。目前，关于如何高效率的进行个人信用评估，种统计学和人工智能方法的改进在国内比较流行。到底具体使用哪种方法？关键是看把个人信用评价问题归结于那类问题而已，可以将其看作聚类问题、分类问题、回归问题，看作不同的问题，那么研究其的方法就是不同的，目前主要的个人信用评估方法有经验式评判法、线性判别方法、统计学方法、运筹学方法、人工智能方法以及一些非参数统计方法。[4]依据这些方法，本文提出了偏最小二乘回归分类个人信用评估方法。

1 理论与方法

1.1 建立个人信用评估框架

个人信用评估问题实际上相当于一个分类问题，依据客户提供的材料将客户分成不同的类别。一般情况下，我们将其分为信用度高的客户和信用度低的客户，依据贷款申请人所交的材料，方方面面考虑各种能够影响其信用的因素，严格尽可能准确地评估出客户失信的几率，从而评估出信用机构风险大小。

在信用评估体系确立好后，那么我们假定每一个客户都会对应n个指标，记为(x1, x2, ..., xn)在这种情况下，就可以将每个客户看成n维空间Rn中的一个点，那么Rn空间中的一类点就可以代表某一类型的客户，于是我们就可以把空间中的超曲面当做分类的界面，依据超曲面进行客户分类，于是信用评估问题转化成了寻找最优分类超平面的数学问题。

在有n个客户的已知类别情况下，可以将这已知的n个客户看成训练样本，设每个客户都会有m个标准，也就是说每一个训练样本具有m个维数，基于以上的假设，我们就可以把有客户的信息用下面的矩阵来表示：

矩阵中的行表示客户，列表示标准，(x1, x2…, xm)这一列反映了评价情况，即xij表示第i个客户对应的第j个标准，yi刻画了第i个客户的信誉度，其中i = 1, 2,…, m；j = 1, 2,…, n.

基于以上内容，则个人信用评价问题就等价于这样一个求最优解的数学优化问题：在n维空间中，我们想法设法获得一个H(x)=0的超曲面，其满足的条件是可以将n维空间中的m个点区分成某些类别，本文中我们 的是两类问题，即将n维空间中的m个点区分成2类的一个超平面。假设（yi=±1，±1代表信誉度高，-1代表信誉度低），在这种训练下倘若有一个未知类别的点x（其代表未知信誉度的客户）我们就可以利用数学分析中的符号函数（如下）进行判别决策。

1.2 偏最小二乘回归建模

1.2.1 数据标准化处理

数据标准化处理的目的就是重合样本点的集合中心与坐标原点。我们文章中所有的标准化都采用z_score标准化[5]处理，它的转化函数为：

在（4）式中，x—表示样本的均值，S(x)代表样本的方差，它的计算方法如下：

为了方便期间，我们将这y1, y2…, yL个因变量与y1, y2…, xm个自变量都处理成标准化的变量。那么因变量组与自变量组的n次标准化观测数据矩阵[6]就可以表示成下面的形式：

1.2.2 提取因变量与自变量的第一对成分，以两者之间的相关性最大为原则

设从自变量中提取出第一成分为t1，从因变量中提取出的一成分记为u1，t1可以表示为自变量集X= (x1, x2…, xm)'的线性组合；即t1=w11x1+…+w1mxm=w1'X，，u1可表示为因变量集Y=(y1…, yp)'的线性组合：u1=v11y1+…+v1pyp=v1'Y为了做出更准确的回归分析，t1和u1的提取要求尽可能在变量组中是比较稳定的信息，即变异的信息很少。另外要求t1和u1之间要有最高的相关性。

根据因变量集的标准化观测数据阵E0和自变量集的标准化观测数据阵F0计算得到第一成分的得分向量，分别用t‾和表示

因为t1和u1的协方差Cov(t1, u1)可通过第一对成分的得分向量—t1和u—1的内积计算，于是，上述问题的约束要求可转化为数学上的条件极值问题：

1.2.3 建立y1…, yp对t1的回归和x1…, xm对t1的回归

设回归模型为：

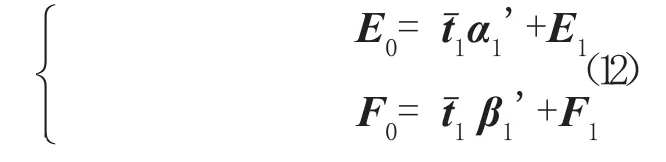
由（12）式可知E0和F0可以用残差矩阵E1和F代替，述步骤可以重复操作。

1.2.4 回归方程计算

设n×m矩阵E0的秩为r≤(n-1, m)，存在r个成分t1, …tr使得：

将tk=wk1x1+…+ωkmxm(k=1, 2…r)，和Y=t1β1+…+trβr联立,化简得到关于p个因变量的偏最小二乘回归式方程：

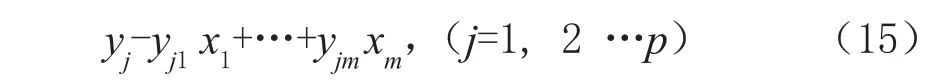
1.3 激活函数

分类的结构性质大部分是由激活函数[7-8]决定，然而激活函数是由实际情况决定的。本文的激活函数用下面的形式简单表示：

在（16）式中，vj表示激活电位，yD表示类别指标，U(yD, ε)是yD的ε邻域，将其称为激活函数的阈值。这里ε的大小可以改变，所以随着ε大小的改变来实现控制分类个人信用评估的正确率的目的。1.4 偏最小二乘回归分类的个人信用评估算法

面对个人信用评估这个分类问题，本文中的输入数据就是可将客户信息矩阵，分类标签就是信用度，在上述理论指导下得到了文本的个人信用评估方法——偏最小二乘回归分类，具体步骤为：

Step 1：搜集原始试验数据，并且将其标准化；

Step 2：完善确定的评估标准规则，将收集到的数据进行数值化处理；

Step 3：得出具体的偏最小二乘回归的模型公式，训练已知的客户类别得到回归方程；

Step 4：确定激活函数，对数据进行训练得到最小二乘回归（即得到最小二乘回归分类器）；

Step 5：试验检测准确性；

Step 6：对未知的客户信用度的样本在此分类器上评估。

2 实证分析

2.1 试验数据

本文中使用的数据是UCI数据库中的德国信用数据，该数据可以从网址：http//erfhive.ucy. uci.edu/kl/.获得，其名称为：UCI Bachine Meaning Reperutory.法国数据共有客户样本1100个，“信用度好”与“信用度差”的样本分为700、400个，按照分类中的称呼将其分为正负客户样本点。其中每个客户样本点具有23个属性，和一个用于判别是否违约的类别标签。

2.2 确定文中的激活函数

本文中说的是客户信用度良好与否的二分情况，应该选择类似于符号函数的函数作为本实验中的激活函数：

式（17）中，f1(x)和f2(x)表示信用度，（类别标号），T为控制值，依具体情况而设定。

特别注意的是，我们可以设定两个控制值，超过一定控制值时判定为“信用度良好好”；低于一定阈值时判定为“信用度较差”，介于两个阈值之间的可以认为是信用度稍微好的，勉强可以，信用机构的风险不会很大。

2.3 实验结果与分析

针对法国客户信用度信用数据的23个属性，我们采用交叉验证方法，得到本实验所需要的成分，经过系列的训练拟合得到了最终的回归方程为：

f(x)=0.0962x1+0.0030x2-0.0432x3+0.0011x4-0.0368x5-0.0131x6-0.0372x7-0.0014x8+0.0243x9-0.0014x10-0.04 71x11+0.0326x12-0.063x13-0.0243x14-0.0135x15+0.1469x16-0.1728x17+0.0565x18+0.0901x19+0.0476x20-0.0407x21-0.0855x22-0.0150x23+1.9682

图 1 法国信用数据标准化下的回归系数直方图

通过画其标准的回归系数图，如图1所示。我们可以从图上直观的看出23个特征属性各自在信用评估中对信用情况的作用，从图可知第二个属性特征对信用评估结果的反映有着较强的作用。且相当的明显。但是，第7个及第12个属性特征就是没有前面的解释作用强烈。相对来说要弱很多。与此同时，我们也将实验结果中阈值对评判结果的影响用表1表示了出来。

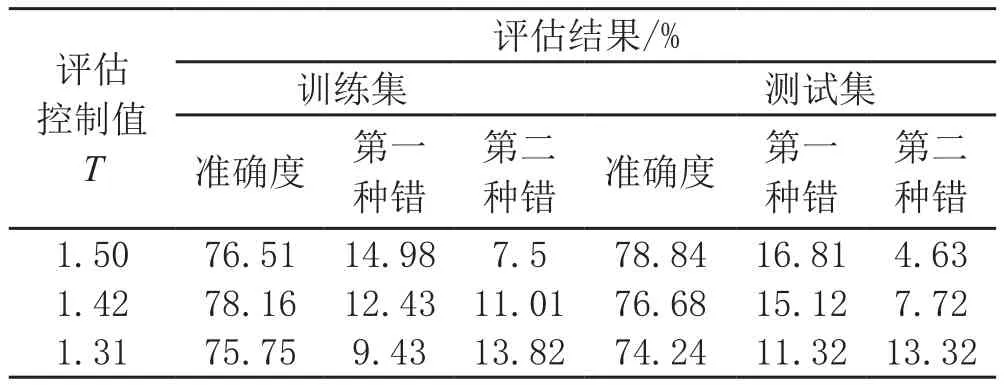
表1 在不同判别阈值下德国信用数据评估结果

3 结论与展望

我们在认真研究了偏最小二乘回归方法的基础上，通过具体的实例构造出了类似于符号函数的激活函数，将二者整合得到了本文中的核心方法---偏最小二乘回归分类方法，且将此方法用在信用评估之中。为了证明此方法的有效性，我们利用德国信用数据在其上进行试验，试验证明了本方法是合理有效的。然而，本文还存在一些不足之处：第一，本文仅使用了一个德国信用数据做实验，而没有使用很多的其他信用数据，对本文方法的合理性缺少更强大的支持；第二，没有详细研究对多等级的或者具有二维及以上的信用评估指标此方法是否仍然具有有效性？没有通过具体的试验进行说明。这些不足都是今后研究需要克服的。

[1]傅铅生.信息系统分析与设计[J].系统设计技术，2010（3）：46-48.

[2]朱敏,谢荣.构建我国个人信用评估体系量大问题之思考[J].黑河学刊，2013（15）：42-43.

[3]孙大利.个人信用评分模型综述与应用分析[J].中国信用卡，2011（13）：12-13.

[4]Durand D.Risk elements in consumer installment financing[M].New York： The Nationl Bureau of Economic Reseach,1998：145.

[5]Altman E I. Financial Ratios,Discriminant analysis and the prediction of corporate bankruptcy[J].The Joumal of Finance, 2001（4）：589-609.

[6]姜明辉，王欢，王雅琳.信用树在个人信用评估中的应用[J].商业研究，2003（12）：15-19.

[7]王雅琳，王欢，黄伟平.K近邻判别分析法在个人信用评估中的应用[J].数量经济技术，经济研究，2004（2）：143-147.

[8]崔伟.基于遗传神经网络的个人信用评估模型的研究[J].计算机工程与设计，2009（18）：4272-4277.

（责任编辑 刘常福）

Least-squares regression classif i cation of personal credit evaluation

DAI Tingting, SHAN Changji, HAN Yan, HU Xiaofei
(1. School of Mathematics and Statistics, Zhaotong University, Zhaotong Yunnan 657000, China; 2. School of Physics Electronic Information Engineering, Zhaotong University, Zhaotong Yunnan 657000, China)

In view of the present commercial bank's credit problems, this paper puts forward the classif i cation based on partial least squares method of personal credit assessment, f i rst, the customer and the corresponding credit indices are made after a matrix; Second, the classif i cation ofpartialleast-squares regression model is set up; Finally, with the model experiment on German credit data, the results are obtained. Simulation results show that the method is feasible, simple and effective.

Personal credit assessment; Partial least-squares regression; The activation function

F224

A

1674 - 9200（2017）03 - 0045 - 04

2016 - 12 - 21

云南省应用基础研究项目（青年项目）“锥度量空间的不动点理论及应用”（2016FD082）。

代婷婷，女，甘肃庆阳人，昭通学院数学与统计学院助教，硕士，主要从事机器学习与智能计算研究；单长吉，男，吉林吉林人，昭通学院物理与电子信息工程学院副教授，硕士，主要从事控制理论与建模研究；韩艳，女，湖北黄冈人，昭通学院数学与统计学院讲师，硕士，主要从事非线性分析研究。