太赫兹表面极化激元∗

张学进陆延青 陈延峰 朱永元 祝世宁

(南京大学现代工程与应用科学学院,固体微结构物理国家重点实验室,人工微结构科学与技术协同创新中心,南京 210093)

太赫兹表面极化激元∗

张学进†陆延青 陈延峰 朱永元 祝世宁

(南京大学现代工程与应用科学学院,固体微结构物理国家重点实验室,人工微结构科学与技术协同创新中心,南京 210093)

(2017年6月28日收到;2017年7月13日收到修改稿)

作为束缚于表面或界面的电磁波与极性元激发的耦合模量子,表面极化激元是克服衍射极限的核心物理.在紫外、可见以及近红外波段,表面等离子极化激元展现出了亚波长特性,具有高分辨成像等应用,并发展成为“表面等离子极化激元亚波长光学”学科;在中红外波段,表面声子极化激元发挥着同样的作用.太赫兹波段曾是人类认识的空白区域,近三十年来得以高速发展,其战略意义重大.具有克服衍射极限能力的太赫兹表面极化激元同样是小型化与集成化太赫兹器件,以及太赫兹超高分辨成像的重要物理基础.近几年来,对以石墨烯为代表的二维材料的研究突飞猛进,诞生了“石墨烯表面等离子极化激元亚波长光学”这门学科,并贡献于太赫兹领域.本文对可在太赫兹波段工作的人工超构材料、掺杂半导体、二维电子气、二维材料、拓扑绝缘体等结构材料的表面极化激元进行了较为全面的总结与介绍,为研制克服衍射极限的太赫兹集成光子学器件提供可资借鉴的物理基础.

太赫兹,表面极化激元,二维材料,近场光学

1 引 言

太赫兹(terahertz,THz)波通常是指频率在0.1—10 THz(波长在30µm—3 mm)波段的电磁波,它的长波段与毫米波(亚毫米波)相衔接,短波段与红外线(远红外)相衔接.太赫兹波是电子学(Electronics)与光子学(Photonics)的交叉领域,长期处于研究的“空隙”(THz gap)领地,如图1所示.

太赫兹波因其独特的“指纹”性、瞬态性、高穿透性、宽带性、相干性和低能性等特征而具有广泛的应用[1-8],如在通信、雷达、天文、医学成像、生物化学物品鉴定、材料学、安全检查等领域.太赫兹波谱、成像与集成器件是非常重要的交叉前沿领域,给技术创新、国民经济发展和国家安全提供了一个非常诱人的机遇.近些年来,各国争先发展太赫兹科学与技术,太赫兹源、探测器以及测量系统的研究已经进入高速发展期.然而,类似于其他电磁波谱段,太赫兹波的衍射极限问题同样束缚着太赫兹光子学器件的小型化、集成化.

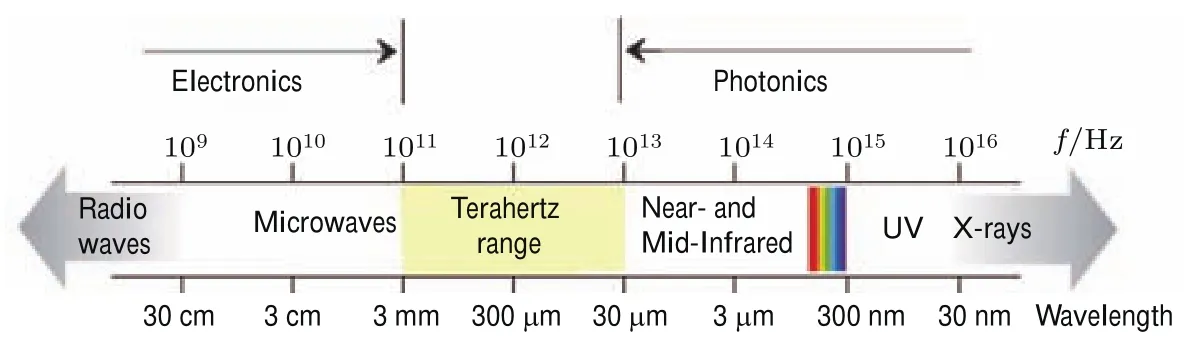
图1 太赫兹在电磁波谱中所处位置的示意图Fig.1.De fi nition of THz waves.

表面等离子极化激元光学(plasmonics)是基于表面等离子极化激元(surface plasmon polaritons,SPPs)发展起来的一门新兴学科,是“表面等离子极化激元亚波长光学(surface plasmon polaritons subwavelength optics)”的简称,主要是研究纳米尺度的光学现象.表面等离子极化激元是电磁波中的电磁场与材料表面的电荷振荡相互谐振的一种元激发,在紫外-可见-近红外波段,一般只有金属材料具有这种集体振荡的性质.加州理工学院的Harry A.Atwater教授在“The Promise of Plasmonics”一文中,将“plasmonics”定义为“一种可以将电磁波压缩到极小结构中,有望产生新一代超快计算机芯片和超灵敏分子探测器的技术”,认为表面等离子极化激元光学元器件最终将可以应用到一系列设备中,极大地改善它们的性能.表面等离子极化激元光学的涉及面非常广泛,包括表面增强拉曼散射[9-14]、表面增强发光[15-23]、表面增强非线性参量过程[24-28]、增强透射[29]、表面增强的能量转移[30-36]、电磁诱导透明[37,38]、表面等离子极化激元纳米波导器件[39]、亚波长纳米激光器[40,41]、克服衍射极限的超分辨成像[42,43],以及超构材料[44]与超构表面[45]等.其应用前景广阔,可被应用于纳米集成电路、纳米集成光路、亚波长光波导、数据存储、克服衍射极限的光成像、光源、太阳能电池,以及生物传感器等.

在太赫兹波段,我们仍从光与物质相互作用这一基本物理问题出发,通过表面极化激元获得亚波长的光场限域.对长波情况,如中红外与太赫兹波,金属表面等离子极化激元失去光场限域本领,而表面声子极化激元[46-50]体现出在克服电磁波衍射极限方面的功能作用以及对器件小型化与集成化的实现能力.本文在重点介绍表面声子极化激元的基础上,介绍了金属超构材料、掺杂半导体、二维电子气以及二维狄拉克材料等可工作于太赫兹波段的表面等离子极化激元;在分析对比表面声子极化激元与表面等离子极化激元各自优缺点的基础上,提出构建混合型表面极化激元是裁剪亚波长太赫兹器件性能的有效途径.

2 极化激元与表面极化激元

在固体物理中引入元激发的概念后一个多体系统便可以简化为一个准粒子体系,这为处理复杂物理问题提供了一条简便的途径.固体中的元激发有很多种类：声子、磁振子和等离子属于集体激发的元激发;准电子、极化子和超导体中由库珀对(Cooper pairs)凝聚形成的Bogolons属于个别激发的元激发;而激子和极化激元属于复合型的元激发.

元激发的概念已经在很大程度上得到了扩展,比如电磁波与固体中的元激发的耦合模量子亦被称为元激发.而电磁波(光子)与极性元激发的耦合模量子被通称为极化激元(polariton),其中电磁波(光子)与声子耦合形成声子极化激元.此外还有磁振子极化激元、等离子极化激元和激子极化激元等,它们分别是光子与磁振子、等离子、激子相耦合形成的新型元激发.

声子极化激元通常是指光子(电磁波)和固体中横振动光学声子(TO格波)的耦合模量子,又被称为“黄子”,这是最先得到研究的极化激元,黄昆先生在这一领域做出了开创性并具有里程碑意义的工作,1951年发表在《关于辐射场和离子晶体的相互作用》的论文中[51].而极化激元概念是在1958年由美国物理学家Hop field研究光子与激子耦合形成激子极化激元时首次提出的[52],随后等离子极化激元、磁振子极化激元等相继被研究者发现.声子极化激元在实验上由美国物理学家Henry和Hop field于1965年在半导体材料GaP的拉曼散射实验中首次观察到[53].迄今,各种极化激元在光学的各个领域中得到深入和广泛的研究与应用.

表面极化激元是极化激元波场束缚于表面或界面的情形,这样的结果会产生明显的优势,如场增强效应以及小型化与集成化器件的研制.表面极化激元不再是纯粹的电磁波模式,如表面等离子极化激元是由电磁波与金属表面的电荷相耦合的模式[54],如图2(a)所示,其场分布束缚于金属/介质的界面;在垂直于界面的方向场强呈指数衰减,如图2(b)所示,显示出束缚、非辐射的倏逝波特征.图2(a)所示的电荷参与的场分布特性限制了激发电磁波的偏振状态,同时较大的欧姆损耗决定了这种表面模式具有非常有限的传播距离.在图2(c)给出的色散关系中,表面模式在光锥的右侧,这一大波矢特性使它具有克服衍射极限的能力,不过其激发产生需要满足动量匹配条件.表面极化激元的存在条件是支持表面极化激元的界面两侧材料的介电函数的实部异号,负的介电函数实部通常伴随着介电异常现象[55],如图2(d)—图2(f)的阴影部分所示.一般来说,结构材料中电磁波出现禁带的频率范围,其介电函数的实部为负,此时其表面/界面可支持表面模式,如光子晶体表面/界面的光学Tamm态[56],光学Tamm态还可与表面等离子极化激元耦合形成Tamm等离子极化激元[57].

图2 表面极化激元的特征[54](a)表面等离子极化激元的横磁模场分布特性;(b)场在垂直于界面的方向上指数式衰减,介质中的衰减长度δd在电磁波的半波长量级,在金属中的衰减长度δm与金属的趋肤深度相关;(c)表面等离子极化激元模式的色散关系;几类极化激元的介电函数曲线[55]：(d)等离子极化激元;(e)声子极化激元;(f)激子极化激元,ε1为介电函数的实部,ε2为介电函数的虚部,ε1在阴影区域小于0Fig.2.Characteristics of surface polaritons[54]：(a)SPPs at the interface between a metal and a dielectric material have a combined electromagnetic wave and surface charge character;(b)this combined character leads to the field component perpendicular to the surface being enhanced near the surface and decaying exponentially with distance away from it.In the dielectric medium above the metal,the decay length of the field δd,is of the order of half the wavelength of light involved,whereas the decay length into the metal δm,is determined by the skin depth;(c) the dispersion curve for an SPP mode shows the momentum mismatch problem that must be overcome in order to couple light and SPP modes together,with the SPP mode always lying beyond the light line,that is,it has greater momentum(ħkSPP)than a free space photon(ħk0)of the same frequency ω;(d)–(f)the illustration of dielectric functions ε1+iε2for plasmon polariton,phonon polariton,and exciton polariton.The corresponding surface polaritons can be supported within the frequency range when ε1＜0,as shown in the shaded area[55].

需要强调的是,在太赫兹波段,简单金属/介质界面的表面等离子极化激元波的束缚能力很弱,几乎等同于自由传播的电磁波,已经不具备克服衍射极限的能力.我们必须寻求其他方案,如金属超构材料、二维狄拉克材料,以及其他类型的表面极化激元,如表面声子极化激元.

3 太赫兹表面声子极化激元

3.1 声子极化激元

不管是否外加电磁场,声子极化激元是极性材料的本征模式,归属于元激发.晶格振动波,即格波与电磁波相互作用,也就是说发生耦合效应是有条件的：1)从电磁波与格波的色散曲线可知,在它们的交点处才可能会发生耦合作用,如图3所示,只有光学振动模能够满足这个条件,两者必须具有相同的频率和波矢;2)在无限空间和体块材料中电磁波是横波,能够与电磁波耦合的晶格振动模也应是横振动模;3)横晶格振动必须是具有极性的,即伴随有旋极化波的产生,极性晶格振动模存在于由不同符号的离子所组成的离子晶体以及所有的压电晶体中.由于电磁波相对于弹性波的速度很大,在色散关系中它是一根十分靠近频率轴的直线,所以与电磁波直接相互作用的晶格振动模的频率非常接近基本固有晶格振动频率(ωTO).实际晶体的基本固有晶格振动频率一般位于1012—1014Hz范围,属于太赫兹至中红外波段.因此,在实际晶体中声子极化激元的产生将会导致太赫兹至中红外的吸收和介电异常现象.

图3 电磁波与横光学模耦合示意图Fig.3.The schematic of the coupling between the electromagnetic wave and transverse optical phonon.

对于离子晶体,正负离子振动时引起极化,伴随有电场的产生,该电场又反过来影响正负离子的振动情况.如果用微观模型来处理上述过程,问题会变得相当复杂,其中涉及极化的微观机理、库仑场作用的长程性、不同晶体结构的退极化场的相异性等.基于这一事实,黄昆先生提出了一对唯象方程,引进宏观电场这一新的物理量来描述离子振动中所受到的库仑力作用,而且宏观电场和离子位移同时对电极化做贡献,这就是黄昆方程的基本结构框架.考虑光学各向同性的双原子离子晶体,黄昆方程可写为[58-60]

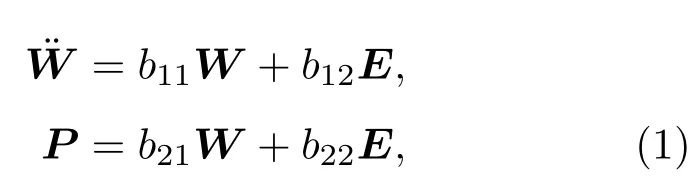
其中W为约化位移,E为宏观电场,P为电极化,系数bij(i,j=1,2)可通过对宏观物理量的测量而获得,由能量守恒定律可以证明b12=b21.与谐振子相类比,该方程中第一式代表运动方程,右边第一项代表弹性恢复力,第二项代表宏观电场附加的恢复力;第二式是极化方程,右边第一项表示离子电荷的位移引起的电极化,第二项则是一般电介质均有的对电场的响应,在这里主要是电子的极化.黄昆方程是一个宏观描述性的方程,不能适用于波长在晶格常数量级的晶格振动,同时它还忽略了非谐力与电矩的高阶项的作用以及阻尼作用,但从实用的角度上具有简洁和有效的特点.

电磁波在真空和介质中的传播速度很快但非瞬时,因此在研究电磁作用时应该考虑其传播速度的存在,这就是电磁推迟效应.将黄昆方程和麦克斯韦方程结合起来,可以得到以下结论[60-63]：1)纵极化场无旋,类静电场,没有电磁性,只是增加恢复力,从而增加振动频率,纵光学声子模不受电磁推迟作用的影响;有著名的LST(Lyddane-Sachs-Teller)关系[64]成立,即ωLO/ωTO=ε(0)/ε(∞)1/2,LST关系反映了静电介电常数ε(0)总是大于高频介电常数ε(∞),以及与极化电场的作用而使长光学纵波的频率ωLO大于长光学横波的频率ωTO之间的一致性;另外,可以看出在离子晶体中由于ωLO/=ωTO,两长光学模简并消除,而它们在非离子晶体中是简并的;2)横极化场有旋,具有电磁性,横光学声子模在长波情形下与光子相互耦合形成新的模式——声子极化激元.声子极化激元的介电函数与Lorentz色散模型理论相符,具有以下方程形式：

这里γ表示材料的阻尼常数,它的量纲同于频率.方程(2)所对应的介电函数曲线形式如图2(e)所示.图4为声子极化激元的色散关系示意图[63],除了图中所示的可区分为类光、类声部分外,一个最显著的特性便是在ωTO与ωLO的频带范围内电磁波不能在晶体中传播.在此波段或频段内介电函数为负,波矢为虚数,如果忽略阻尼作用,在这种频率范围内从外部入射到晶体的辐射将被完全反射,这一频率范围常被称为剩余辐射带(reststrahlen band).利用这一效应可以获得准单色光,从而可与光子晶体、声子晶体等一道归于人工带隙工程的候选者行列.

一般来说,极性材料中,原子间的键合越弱、原子越重,则声学声子的声速越小,光学声子的振动频率也越低;同时,相邻原子质量差越大,原子间的键合强度一般也会下降,从而光学声子频率降低.自然界中,ωTO处于太赫兹波段的极性晶体为数不多,它们有GaAs[65,66],InP[67],CaF2[68]等. 图5为GaAs晶体在剩余辐射带附近的反射谱[69].

3.2 人工声子极化激元

从下文我们将会看到,等离子极化激元的响应频率由自由电荷浓度决定并调节,而离子晶体支持的声子极化激元没有这样的可调性与灵活性.但声子极化激元具有更低损耗等优势,可在太赫兹波段任意位置响应的声子极化激元为人们所期待.我们考虑在离子晶体中引入有规则的缺陷,构成人工超结构,通过结构周期大小来改变产生剩余辐射带的位置.

从广义上讲,具有压电、压磁性质的材料经规则排布后,其振动形成的宏观电/磁极化可与电磁波相互作用,耦合谐振产生声子极化激元,我们称之为压电/磁超构材料.压电/磁超构材料较离子晶体有着很多新奇的地方,在离子晶体中,声子极化激元只能由电磁波与横振动光学格波的耦合产生,而在压电/磁超构材料中,电磁波可与声学格波相耦合,不仅可与横振动声学格波耦合,还可以与纵振动声学格波耦合.更重要的是压电/磁超构材料可将声子极化激元的光子-声子耦合位置从红外波段下移至太赫兹甚至更低波段,同时带隙大小也具有可调节性,这些为太赫兹领域注入了生机与活力,为实际应用提供了新的思路.根据实际需要,人们可通过调整压电/磁超构材料的周期大小来获得满足要求的工作频段,通过选材等手段来获得所需带隙大小,我们称这种具有灵活性与可调性的压电/磁超构材料中的声子极化激元为人工声子极化激元.

对于压电超构材料,通过声场运动方程[70]：

其中T,u和ρ分别代表应力、粒子位移以及材料密度.根据方程(3)和应变-位移关系S=∇su,得到

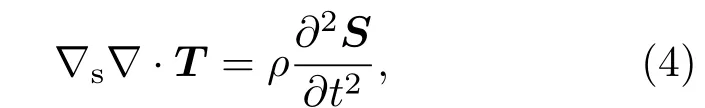
加上压电本构方程

其中T,S,E和D分别表示应力、应变、电场强度和电位移;CE,e和εS分别是短路弹性、压电和受夹介电张量.其中i,j=1,2,3;I,J=1,2,3,4,5,6.

这里我们以由铌酸锂(LiNbO3)或钽酸锂(LiTaO3)晶体组成的压电超构材料为例,因为铌酸锂是一种铁电材料,可以经由铁电畴工程技术制备压电超构材料.铌酸锂晶体属于3m点群,电畴的自发极化沿z方向,正负电畴的晶体学坐标之间的关系是绕x轴旋转180°[71],可以构建如图6所示的一维排列情况[72].因此,正负电畴的奇数阶张量的所有元素将具有相反的符号,如在方程(5)中,即只有压电张量在正负畴发生变号.

选取图6(a)所示的沿x轴方向排列电畴的结构,由方程(4)和方程(5)可得到纵振动的运动方程：

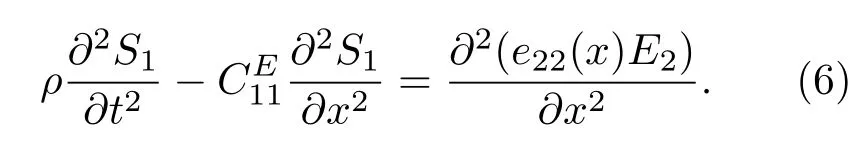
图6 由铁电畴构成的一维压电超构材料示意图[72](a), (b)表示两种排列构型,箭头方向表示自发极化方向;在人工声子极化激元的介电异常处,压电超构材料的表面/界面处支持表面人工声子极化激元Fig.6. The schematic diagram of one-dimensional piezoelectric metamaterials with the ferroelectric domains arranged along(a)x or y axis,and(b)z axis.The arrows present the spontaneous polarization direction of ferroelectric domains.Arti fi cial surface phonon polaritons exist at the surface/interface of piezoelectric metamaterials[72].

图7 压电超构材料中太赫兹人工声子极化激元的介电函数曲线 ε1为介电函数的实部,ε2为介电函数的虚部;阻尼常数为γ=0.01ωLO,在ε1小于0的区域支持太赫兹表面人工声子极化激元Fig.7.The calculated dielectric function curves of an arti fi cial phonon polariton operating around 1 THz in the piezoelectric metamaterial illustrated as Fig.6(a). The real and imaginary parts of dielectric function is ε1and ε2respectively.For safety,a rather large damping constant γ=0.01ωLOis chosen.The arti ficial surface phonon polariton can be generated when ε1＜0.

从方程(6)可以看出,压电超构材料类似于一个受迫振子,电磁波将激发出沿x轴传播的纵声波.通过一定的数学处理[73-76],得到形式如方程(2)的压电超构材料的等效介电函数.进一步计算显示,选取周期为几十纳米时,人工声子极化激元位于1 THz附近,考虑实际损耗,以较大的阻尼常数γ=0.01ωLO代入计算出的介电函数如图7所示.

因此,对人工声子极化激元的研究不仅有基础研究的意义,还具有很大的开发潜力与应用前景.根据其特殊的物理性质,可望开发出一些新型的光学器件和声学器件.

3.3 表面声子极化激元

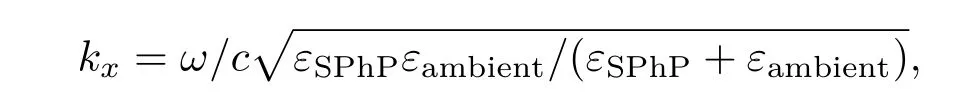
与表面等离子极化激元类似,单界面表面声子极化激元的色散关系εSPhP与εambient分别是离子晶体与环境材料的介电函数,其色散曲线如图8(a)所示.与图2(c)表面等离子极化激元的色散曲线具有类似性,其激发需满足动量匹配条件,且具有更大的色散性.虽然存在范围窄(ωTO与ωLO之间的区域),但较表面等离子极化激元有低损耗的优势.

图8 (a)离子晶体[77]及(b)压电超构材料[50]与空气界面的表面声子极化激元的色散关系,表面声子极化激元出现于声子极化激元的剩余辐射带(亦见图4所示)Fig.8.The dispersion curves of surface phonon polaritons in(a)ionic crystals[77]and(b)piezoelectric metamaterials[50].In(a),the dispersion curve of corresponding phonon polariton is a guide for the eyes,as well as those of photons in the low and high frequency limit,and in air;in(b),kp=50 cm-1.

图8(b)所示为压电超构材料的表面人工声子极化激元,其色散曲线与图8(a)相似[50,78].其场分布束缚于超构材料的表面,在垂直于界面的方向场强呈指数衰减,具有倏逝波特征,如图6所示.表面人工声子极化激元的工作频段具有可调性,适合构建工作于太赫兹波段的表面声子极化激元,为太赫兹波段克服衍射极限器件的研制提供了新的方案与途径.

4 太赫兹表面等离子极化激元

工作于可见光波段附近的表面等离子极化激元主要由金属Au,Ag,Al,Cu等支持,在太赫兹波段,这些金属的介电函数实部的绝对值较一般介质材料的大两三个数量级,这时表面等离子极化激元的色散曲线非常接近于介质材料中的光线,从而失去高束缚能力及场增强等特有意义.

这一问题的本质在于金属中电子浓度过高,约1022—1023cm-3.在表面等离子极化激元色散关系中,以Drude模型简化金属的介电函数εm=得到表面等离子极化激元的渐近频率其中等离子体频率分别表示自由电荷的浓度、有效质量及基本电荷,ε0是真空介电函数.从上述可以得知,金属的表面等离子极化激元只在紫外-可见光-近红外波段性能优异,另一方面,ωp随电荷浓度可调,因此太赫兹表面等离子极化激元可通过稀释自由电荷浓度的途径来获得.

4.1 表面人工等离子极化激元

如图9(a),在金属表面挖沟槽或打孔形成的超构材料[79],等效于平均电荷浓度的降低.类似于光子晶体的效能,在具有周期图案化的金属表面,传播的表面等离子极化激元会因经受布拉格(Bragg)反射而形成能带结构,在布里渊区(Brillouin zone)边界,带隙打开,如图9(b)所示,具有与图2(c)的类似特性.这类表面等离子极化激元常被称为spoof SPPs或designer SPPs[79-82].可基于此开展设计一些太赫兹表面等离子极化激元器件,如图10所示的能量聚焦结构[83].

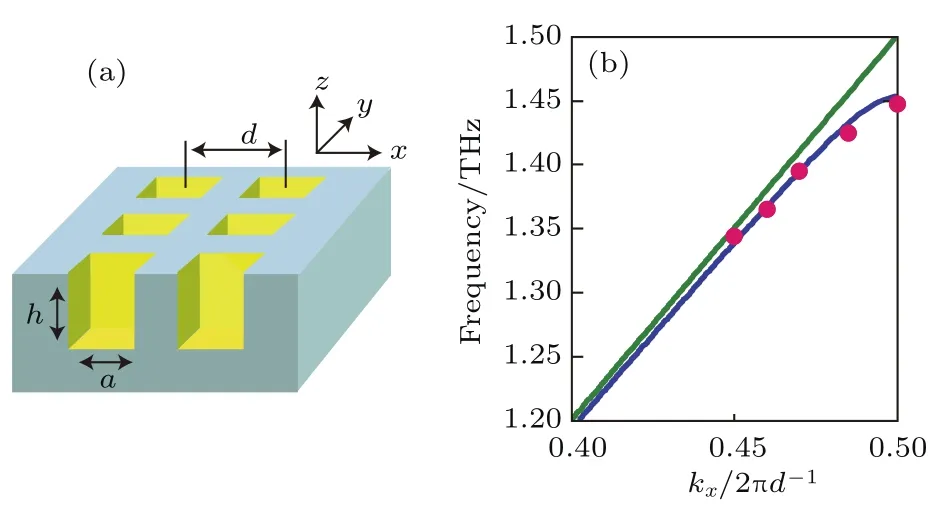
图9 可支持太赫兹表面等离子极化激元的金属超构材料[79](a)金属超构材料示意图;(b)表面等离子极化激元的色散关系Fig.9. Plasmonic metamaterials working at THz range[79]：(a)Schematic of the plasmonic metamaterial showing holes in yellow;(b)SPP dispersion curve near the Brillouin zone boundary.The green curve indicates the light line,the blue curve is calculated by modal expansion approximation,and red points are from fi nite-di ff erence time-domain simulation.

图10 刻有凹槽结构的锥形完美导体的太赫兹波汇聚作用[83]Fig.10.Superfocusing on a corrugated cone of length 2 mm,with constant groove depth h=5µm and period d=5µm.Cylinder radius R is reduced from 100 to 10µm.The plot shows the magnitude of the E field on a logarithmic scale spanning 2 orders of magnitude[83].

4.2 掺杂半导体的表面等离子极化激元

半导体工业对人类生产与生活产生了巨大的影响,在Si电子芯片走向纳米级工艺制造的同时,光通信领域的Si基光子学与光子集成芯片的发展日益成熟.半导体Si的掺杂分为n型和p型,其掺杂浓度N与等离子体频率ωp的关系已得到研究[84],采用中等掺杂程度N ≈1016cm-3的n型Si,其等离子体频率ωp在太赫兹范围.太赫兹时域谱(THz-TDS)是有效的样品测量手段,对太赫兹表面等离子极化激元的测量需附加上如图11(a)所示的耦入-耦出装置[85].图11(b)给出的是掺杂浓度N≈1018cm-3的n型Si光栅的表面等离子极化激元透射谱信号[86],对时域信号进行傅里叶变换(Fourier transform)T=t(ω)exp[iφ(ω)],t(ω)是振幅,φ(ω)是相位,由振幅t(ω)得到的频域透射谱如图12所示[87].这一结果与n型Si光栅的表面等离子极化激元的能带结构一致,即传播的表面等离子极化激元因布拉格反射在布里渊区边界带隙打开,形成禁带,在透射谱上表现为透射率的急剧降低.对相位φ(ω)数据进行处理,可得到表面等离子极化激元的色散关系[86],如图13所示.

图11 掺杂Si光栅表面传播的太赫兹表面等离子极化激元的时域谱测量 (a)太赫兹表面等离子极化激元的实验测量装置示意图,太赫兹脉冲在右端空隙处激发产生表面等离子极化激元,传播到左端空隙处耦合出射[85]; (b)掺杂浓度N≈1018cm-3的n型Si光栅的时域透射谱[86],插图是Si光栅的电子显微镜图Fig.11.(a)Experimental setup used for exciting THz SPPs on the sample[85],the incoming THz beam is focused on the incoupling aperture controlled by razor blade K1,the SPPs travel along the sample surface/interface until scattered at the outcoupling aperture controlled by another razor blade K2;(b)THz SPP transients,the gray curve corresponds to SPPs propagating on a fl at n-doped Si surface with a carrier density of N ≈ 1018cm-3,the black curve corresponds to a SPP transient transmitted through a grating of 30 grooves with a lattice constant of 442µm, groove depth of 100µm,and groove width of 221µm structured on a similar Si wafer;inset,scanning electron microscope image of an SPP grating[86].

图12 对时域信号进行傅里叶变换后得到的掺杂Si光栅的太赫兹透射谱[86]Fig.12.Transmittance as a function of the frequency of SPPs propagating on gratings of grooves structured on Si wafers.The open circles are measurements and the solid curves numerical calculations：(a)Corresponds to a grating structured on n-doped Si with a carrier density of N ≈ 1018cm-3,while(b)corresponds to a similar grating structured on p-doped Si with a carrier density of N ≈1019cm-3[86].

图13 掺杂Si光栅所支持的表面等离子极化激元的色散关系[86]Fig.13.Dispersion relation of SPPs on a grating of grooves structured on an n-doped Si wafer.The open circles are measurements,while the solid curve is a calculation.The dashed curve represents the dispersion relation of SPPs on a fl at Si surface[86].

对掺杂Si的太赫兹表面等离子极化激元的研究,利于太赫兹与Si基光子学的融合,借鉴Si基光子学的成熟技术与工艺,发展太赫兹科学与技术,研制克服衍射极限的Si基太赫兹集成器件.

4.3 二维电子气

二维电子气(two-dimensional electron gas, 2DEG)是指电子气可以自由在二维方向移动,而在第三维上受到限制的现象.它是许多场效应器件(例如金属-氧化物-半导体场效应管(metal-oxidesemiconductor field-e ff ect transistor,MOSFET)与高电子迁移率二极管(high electron mobility transistor,HEMT))工作的基础.二维电子气存在于掺杂半导体与绝缘层界面的反转层中,与石墨烯(graphene)相比,二维电子气属于一薄层,在层厚的方向自由电荷浓度具有一定的分布,其中电荷浓度可由栅极偏压调控,电荷类型可以是电子或空穴.因为光学响应发生在界面,较为合适的是用面电导率来描述其光学性能,二维电子气的面电导率可近似写成Drude表达式[87]：

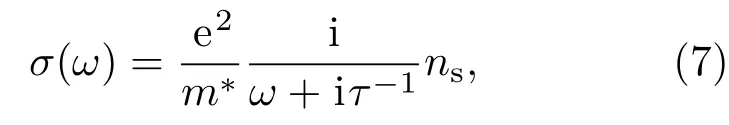
m∗,ns,τ,e分别表示自由电荷的有效质量、面电荷浓度、弛豫时间及基本电荷.太赫兹响应所需的面电荷浓度ns在1012cm-2量级,如图14所示,面电荷浓度越大,响应频率越高[88].

图14 随面电荷浓度改变太赫兹响应的Si金属-氧化物-半导体场效应晶体管[88]Fig.14.Resonance position versus electron density ns.The solid circles are the data from experiments. The solid curve is the calculated.Inset：the schematic of cross section through Si MOSFET with transparent gate and grating overlay[88].

二维电子气中等离子的集体振荡及其表面等离子极化激元的物理特性较早地得以研究[89,90],我们将在5.1节与石墨烯一并做比较性介绍.

5 二维材料的太赫兹表面极化激元

二维(two-dimensional,2D)或范德瓦耳斯(van der Waals,vdW)材料是材料科学和凝聚态物理领域迅速发展的一个研究热点.图15对二维材料中的极化激元予以概括性归总[91],包括二维等离子极化激元、声子极化激元、激子极化激元、库珀对极化激元、磁振子极化激元等.这里我们介绍工作于太赫兹波段的二维狄拉克(Dirac)等离子极化激元与声子极化激元.

5.1 二维表面等离子极化激元

二维等离子材料在本质上属于二维电子气系统,进一步与传统的二维电子气对比,二维材料的特殊性表现在第三维上受到更大的限制,即被限制于晶格原子周期性排布的单或多原子层中.石墨烯就是这样一种具有六角蜂窝状点阵结构的单原子层,物理性质来源于其独特的电子能带结构,如图16所示,能量为正的导带和能量为负的价带交汇于一点,形成零带隙,就像在零质量极限下的相对论狄拉克方程里正电子和负电子的能带在零动量处汇合一样.因此,在石墨烯中布里渊区边界的交汇点通常被称作狄拉克点(Dirac point)[92].

图15 各类二维材料及其极化激元种类[91]Fig.15.Polaritons in vdW materials[91],vdW polaritons exhibit strong con fi nement,as de fi ned by the ratio of incident light wavelength λ0to polariton wavelength λp.

图16 石墨烯的电子能带结构[92]Fig.16.Electronic dispersion in the honeycomb lattice[92]：Left,energy spectrum;right,zoom in of the energy bands close to one of the Dirac points.

石墨烯的面电导率由带内跃迁项σintra与带间跃迁项σinter两部分组成[93],带内跃迁与带间跃迁过程分别如图17(a)插图中的1○与2○所示.太赫兹波段,在高掺杂情况下,即ħω≪EF[EF为费米(Fermi)能,ħ为约化普朗克常数(reduced Planck constant),有时称为狄拉克常数(Dirac constant)]时,石墨烯的面电导率由带内跃迁项σintra决定,可近似写成Drude表达式[94]：

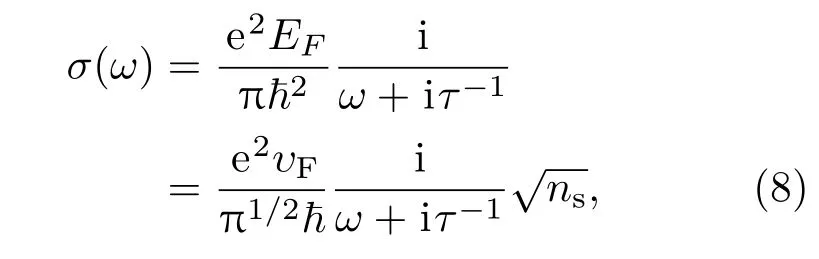
其中υF为费米速度,υF≈106m/s.比较方程(7)与方程(8),石墨烯为零质量电子狄拉克锥的线性能带,面电导率σ(ω)∝n1/2s,而二维电子气的电子能带结构呈抛物带型[如图17(b)中的插图所示],其面电导率σ(ω)∝ns.前者的等离子体频率ωp∝n1/4s,后者的等离子体频率ωp∝n1/2s.图17给出了石墨烯与二维电子气的表面等离子极化激元在相同面电荷浓度ns=1013cm-2情况下的对比.从图17的色散曲线可知,石墨烯与二维电子气的太赫兹表面等离子极化激元的束缚能力不强,但在中红外波段的传播波长较真空波长小两个数量级左右,具有非常高的局域性,即被约束体积达到衍射极限的10-6倍.

有限尺寸石墨烯与二维电子气的棱边处所支持的表面等离子极化激元边模(edge mode)具有大的局域程度,可实现太赫兹波段的强束缚能力,其色散曲线如图18(a)和图18(b))所示,石墨烯带的单极(monopole)边模色散曲线呈ω∝q1/4的关系,而二维电子气带很快拉平为与波矢无关的局域特征[95],这些特性与方程(7)和(8)所描述的面电导率紧密相关.石墨烯带的太赫兹表面等离子极化激元边模与波导模的传播示意图如图18(c)所示[96],这种极强的局域化不但可用来增强光与物质的相互作用,而且可大大降低亚波长光波导的弯曲损耗[97].石墨烯及二维电子气也因此成为克服衍射极限的太赫兹集成光子学器件及芯片的重要载体.

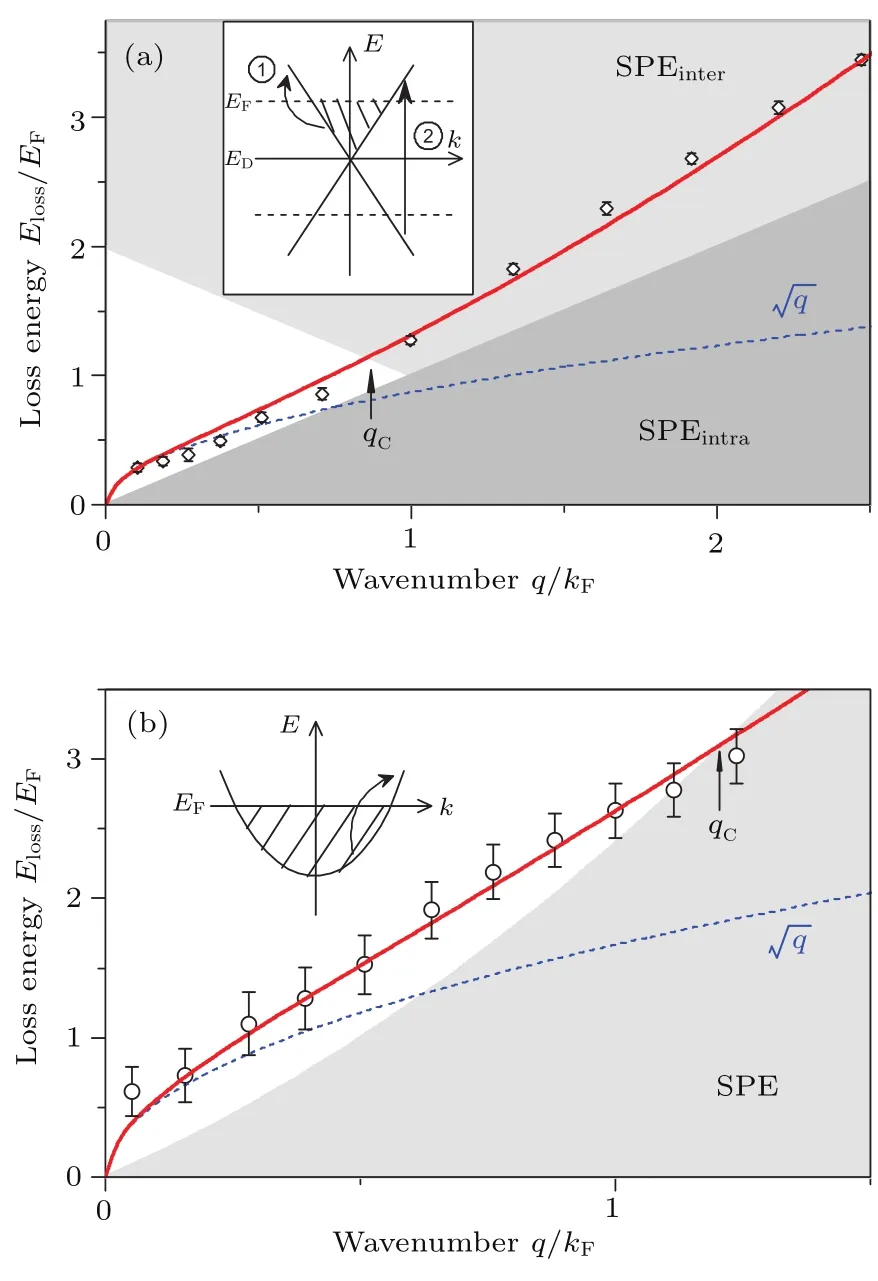
图17 (a)石墨烯与(b)二维电子气表面等离子极化激元的色散关系[93]Fig.17.Plasmon dispersion for(a)graphene of similar charge density(EF=0.57 eV,n～2×1013cm-2) and(b)Si(111)-Ag surface-state band(EF=0.19 eV, n～ 2×1013cm-2).The respective band structures(inset diagrams)show the origin of single-particle excitations(SPEs)1○ intraband and 2○ interband. Graphene is ambipolar with electron and hole carriers in separate π,π∗bands.qcindicates the onset where plasmon enters the damping region.The blue dashed curves correspond to q1/2dispersion of free 2DEGs with the same electron density,and the red full curves correspond to best fi ts to experimental results using high-resolution angle-resolved re fl ection electron-energy-loss spectrometer(HREELS)[93].

石墨烯及其微纳结构已经成为太赫兹领域的一颗冉冉升起的新星.双层石墨烯、石墨烯纳米带、纳米盘等存在带隙,并且禁带宽度可调,多层石墨烯结构可制成P-I-N结,应用于太赫兹等波段的光电探测、生物传感、可调激射等.

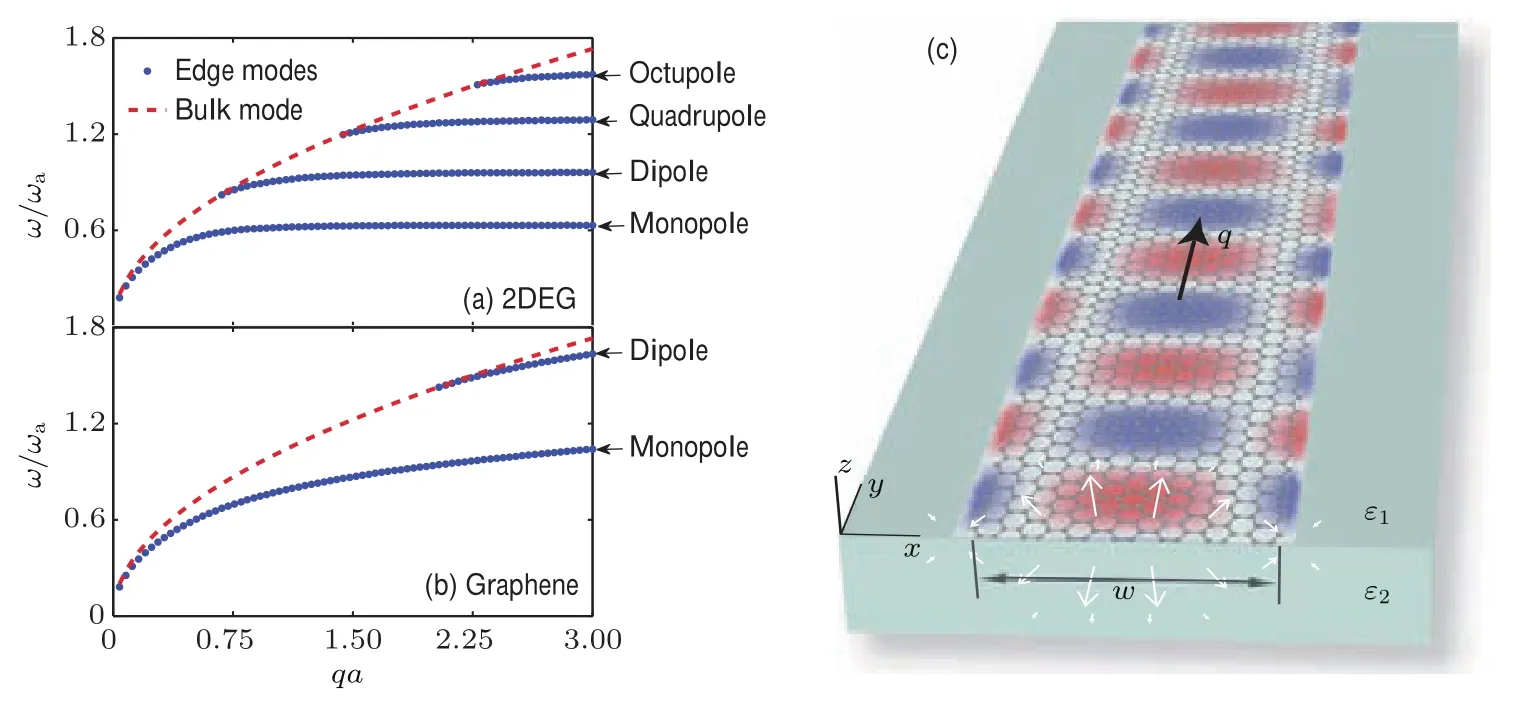
图18 有限尺寸的(a)二维电子气与(b)石墨烯的表面等离子极化激元边模的色散关系[95]及其(c)太赫兹波段的边模及波导模的传播特征[96]Fig.18.Calculated edge plasmon polariton dispersions for(a)2DEG and(b)graphene with the edge layer width a,in the 2DEG andin the graphene,where ε is the background dielectric constant[95];(c)THz edge and waveguide modes.A graphene ribbon of the width w placed at the interface between two dielectric half spaces with dielectric constants ε1and ε2,the mode propagates along the y axis.The color plot presents THz electric field x-component spatial distribution in the x-y plane,and the arrows correspond to the electric field lines in the x-z plane[96].

图19 拓扑绝缘体Bi2Se3的(a)电子能带结构[98]与(b)太赫兹表面等离子极化激元色散关系[99]Fig.19.Electronic dispersion and plasmon dispersion in topological insulator Bi2Se3：(a)The surface states with a single Dirac cone,the warmer colours represent higher local density of states(LDOS)on the[111]surface;the red regions indicate bulk energy bands and the blue regions indicate bulk energy gaps;the surface states can be clearly seen around the Γ point as red lines dispersing in the bulk gap[98];(b)experimental and theoretical dispersion of plasmons in Bi2Se3[99].Main panel is experimental plamon dispersion at 6 K(blue circles)compared with the calculated plasmon dispersion for Dirac(dashed black line)and massive(dotted blue line)electrons,the additional point(green diamond)refers to a seventh sample with ribbon width W=1.8µm and period L=4µm;inset：linear dependence of plasmon frequency vpon W1/2.

拓扑绝缘体的表面态也具有狄拉克电子能带结构.拓扑绝缘体是一种内部绝缘、界面允许电荷移动的材料.在拓扑绝缘体的内部,电子能带结构和常规的绝缘体相似,其费米能级位于导带和价带之间.拓扑绝缘体的表面存在完全由体电子态的拓扑对称结构所决定的、与表面具体结构无关的、不受杂质与无序影响的稳定量子态,这些量子态位于块体能带结构的带隙之中,具有不同自旋的电子运动方向相反.图19(a)所示的拓扑绝缘体Bi2Se3的电子能带结构表明,在Bi2Se3的约0.3 eV的块体能带结构的带隙之中存在穿越能隙的表面狄拉克电子态[98].拓扑绝缘体表面态的太赫兹表面等离子极化激元的色散关系遵循与石墨烯一致的零质量狄拉克电子的规律,如图19(b)所示[99].

此外,双层石墨烯、过渡金属二硫化物、黑磷等二维材料也具有表面等离子极化激元效应.

5.2 二维表面声子极化激元

六角氮化硼(hexagonal boron nitride,hBN)提供各向异性的极性光学声子,在不同轴向上的介电函数会有异号现象,从而具有双曲超材料的性质[100].六角氮化硼的双曲声子极化激元特性发生在中红外波段,而拓扑绝缘体材料Bi2Se3和Bi2Te3除了可见、近红外波段,在太赫兹波段也具有双曲超材料性质[101].从图20所示的介电函数曲线可以预知拓扑绝缘体材料Bi2Se3的性能及其应用,在区域A与C表现为双曲性,区域B为剩余辐射带.其表面模式的色散关系类似于图8所示,双曲型声子极化激元的波导模式,以及与表面等离子极化激元的耦合将在后文中讨论.

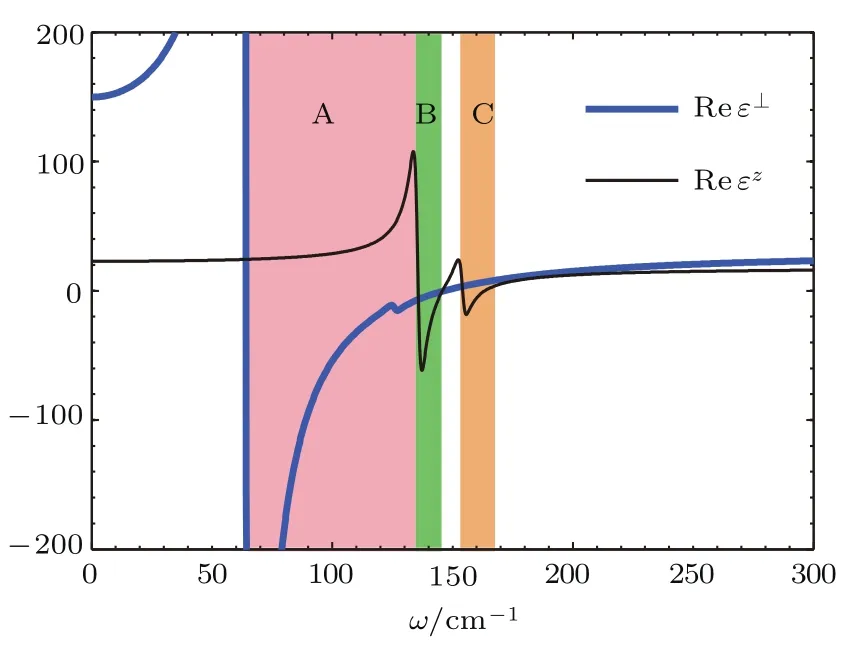
图20 拓扑绝缘体Bi2Se3的太赫兹介电函数及其双曲性[101] Fig.20.The real parts of the tangential and axial permittivities of Bi2Se3.The sign changes of the permittivities are due to the Euand A2uphonons.Surface-and bulk-con fi ned collective modes exist inside the spectral regions where at least one of the permittivities is negative.They include the type-II hyperbolic region A(Reε⊥＜ 0,Reεz＞ 0),the reststrahlen region B(Reε⊥,Reεz＜ 0),and the type-I hyperbolic region C(Reε⊥＞0,Reεz＜0)[101].

6 表面声子极化激元与表面等离子极化激元的比较

一般情况下,表面声子极化激元与表面等离子极化激元的材料载体与工作波段不同,前者为介质,主要工作在中红外波段,后者为金属,主要工作在紫外、可见及近红外波段.表面极化激元的寿命取决于极化激元的寿命情况,极化激元的寿命又以元激发本身的寿命为上限.因散射机理不同,极性材料中的光学声子寿命较长,达到约1—100 ps[67,102],相邻原子质量差越大,光学声子寿命越长,而晶格类型对光学声子寿命的影响不大.金属中的自由电荷寿命约为10 fs[103-105].在声子极化激元的Lorentz型介电函数方程(2)中,阻尼常数γ在1012s-1量级,金属中等离子极化激元的Drude型介电函数方程中的阻尼系数γ在1014s-1量级,两者相差两个数量级.作为估算,表面声子极化激元模的寿命会比声子的寿命小约4—10倍[47],但仍比表面等离子极化激元模的寿命长1—2个数量级[104].从这一点来看,表面声子极化激元因低损耗而使得应用前景更为诱人.

如图8所示的色散关系,表面声子极化激元的色散性强,群速度较低,使得其传播长度不会比表面等离子极化激元的大很多.中等或重掺杂的半导体支持太赫兹表面等离子极化激元,阻尼系数γ在1013s-1量级,损耗低于金属中的,但因等离子频率ωp也小了约一个量级,所以由ωp/γ所标定的综合性能不一定优于金属的.此外,工作于太赫兹的二维电子气的面电导率方程(7)及二维狄拉克材料的面电导率方程(8)中的阻尼常数都在1011s-1量级,自由电荷寿命比金属中的大,约为500 fs[106].二维材料中电子自由化程度低,自由电荷浓度小,这不但使其能够工作于低频的太赫兹波段,同时也使电子-声子与电子-电子等散射变弱,从而具有高的迁移率.单层石墨烯、双层石墨烯、硫化钼、黑磷及1 nm厚Au的表面等离子极化激元的光场束缚及波传播性质如图21所示,它们是在温度300 K、面电荷浓度ns∼1012cm-2、n-型掺杂、SiO2(介电函数2.25)基板等相同条件下进行对比的.从图21给出的几种二维材料的表面等离子极化激元性质可知,二维材料的高局域程度、低损耗性能主要体现在中红外波段,相较起来,在太赫兹波段的表现并不十分诱人.人们可通过结合表面声子极化激元、表面等离子极化激元及二维表面等离子极化激元等的优点,产生具有所需优异性能的混合型表面极化激元,后面将举例介绍.

图21 几种二维材料的表面等离子极化激元特性[55]Fig.21.Calculated con fi nement factor β,which is obtained by normalizing the free-space wavelength to the con fi ned wavelength,and fi gure of merit of propagation property Γ-1,for various 2D materials such as graphene,bilayer graphene,black phosphorus(BP),and MoS2.Γ-1/(2π)gives the number of cycles the 2D plasmon polariton can propagate before its amplitude decays by 1/e.Result for Au monolayer is shown for comparison.BP exhibits highly anisotropic in-plane electronic dispersion,with e ff ective masses along the two crystal axes di ff ering by a factor of～10.Both the high(x)-and low(y)-mass directions are displayed[55].

声子寿命依赖于内禀的声子-声子散射,外在的缺陷、杂质以及表面粗糙等进一步降低其寿命,因此高纯、高质的单晶体材料成为优选.在低频的太赫兹波段,声子寿命更长些,工作于太赫兹波段的人工声子与超结构相联系,作为缺陷本质的结构界面会带来额外的声子散射.为降低这一损耗,宜采用单晶畴结构,因此铁电畴工程技术值得深入探索与研究,使压电/磁超构材料成为低损耗人工声子极化激元实用化的材料载体,并进一步开拓出新型太赫兹功能器件.为提高表面等离子极化激元的性能,人们也在不断地尝试抑制表面散射损耗的工艺及降低材料欧姆损耗的制备方法,如金属撕膜工艺(template removal)[107]、外延生长(epitaxial growth)[41]、原子层沉积(atomic layer deposition)[108]及单晶(single-crystalline)合成[109,110]等.

7 混合型太赫兹表面极化激元

如前所述,太赫兹波段的表面极化激元具有各自的优缺点,如表面声子极化激元的损耗低但工作频段窄,二维表面等离子极化激元具有可调性但传播不够远等,若能构建它们的耦合模式,则可结合各自的优点,起到取长补短、相得益彰的效用.

7.1 表面声子-等离子极化激元

掺杂半导体中自由电荷与极性声子同时存在,则声子与等离子有可能相互耦合.这里我们举两个自由电荷与极性声子各自的载体相分离的例子.图22所示为掺杂半导体或金属超构材料与压电超构材料组成的结构,各自所支持的极性人工声子与等离子在近场范围内相互作用,在界面处产生太赫兹混合型的表面声子-等离子极化激元,它的带隙大小依赖于压电超构材料的厚度及二者间的耦合强度,这一耦合强度决定于压电超构材料的机电耦合系数,其值越大,带隙越大[50].图23显示了压电超构材料的结构重要性,结构是形成宏观电极化,并与太赫兹波相互耦合的基础.结构可以具有周期性、非周期性或准周期性,从而在太赫兹响应频谱上具有相应规律的分布,这为太赫兹亚波长多波复用(wavelength division multiplexing,WDM)器件提供了物理基础与新途径.基于压电超构材料的特殊功能以及亚波长结构性质,这种表面声子-等离子极化激元可以通过声波激发,也可以通过电驱动产生,从而为太赫兹亚波长器件提供了多样性与灵活性[50].

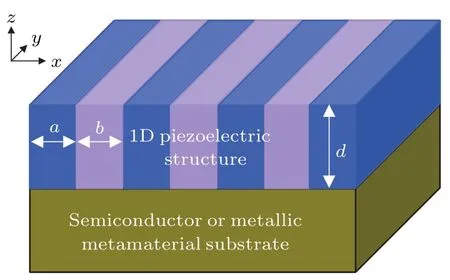
图22 太赫兹表面人工声子-等离子极化激元结构示意图[50]Fig.22.Schematic of a one-dimensional piezoelectric metamaterial fi lm in contact with a semi-in fi nite semiconductor or metallic metamaterial substrate.The stripes periodically arranged along the x axis represent two components with di ff erent piezoelectric coeffi cients.a and b denote the widths of two components and d the thickness of the fi lm[50].

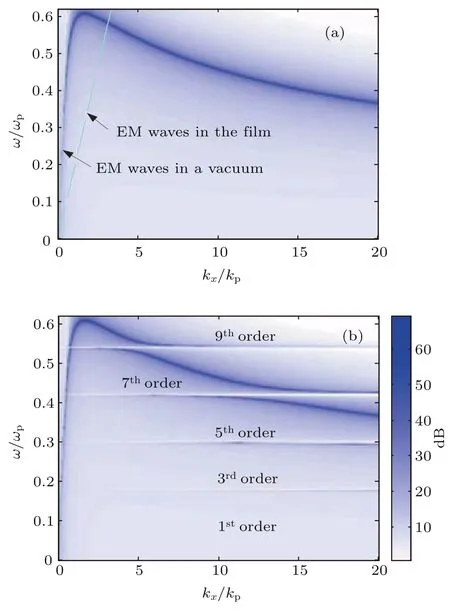
图23 太赫兹 (a)表面等离子极化激元与(b)表面人工声子-等离子极化激元的色散关系[50]Fig.23.The dispersion curves of(a)surface plasmon polaritons for a similar layered system shown in Fig.22,where the metamaterial fi lm is replaced by a 200-nm-thick LiNbO3fi lm textured with the c axis normal to the substrate,and(b)surface phononplasmon polaritons for the layered system shown in Fig.22.Two components in Fig.22 correspond to a textured 200-nm-thick LiNbO3of width of 20 nm with the+c axis along the+z direction and the-c axis along the+z direction.The labels denote the order numbers of transverse“phonon polaritons”woven into the surface plasmon polaritons[50].

相较于其他二维材料,拓扑绝缘体的优势不仅表现在其支持太赫兹声子极化激元,而且表现在制备工艺的简易性上,它不像一般二维材料那样需要精确的层厚控制与转移技术,作为其表面态的二维表面等离子极化激元存在于其表面/界面处.图20所示的介电函数曲线中,Bi2Se3在区域A与C表现出双曲特性,其等频面如图24(a)所示.图24(b)示意出声子极化激元与二维表面等离子极化激元分别被支持的空间区域位置,后者存在于拓扑绝缘体的表面/界面.在不掺杂情况下只出现声子极化激元模式,如图25(a)与图25(d)所示.图25(a)—图25(c)是石墨烯/六角氮化硼/石墨烯结构的模式色散图,这里作为对比使用.六角氮化硼与拓扑绝缘体Bi2Se3都具有双曲性,石墨烯/六角氮化硼/石墨烯结构与Bi2Se3表面/Bi2Se3/Bi2Se3表面在结构特性上相似,即各向异性的双曲材料被夹于两层狄拉克自由电荷层中,只是前者工作在中红外波段,后者工作于太赫兹波段.有限厚的双曲材料层支持波导模式,如图25(a)与图25(d).与图20相应,图25(d)中出现了明显的3段不同模式组.双曲材料层的厚度越小,波导模式数越少,如图25(b)与图25(c)以及图25(e)与图25(f)之对比.在掺杂情况下,表面层出现表面等离子极化激元,并与声子极化激元相耦合,形成表面声子-等离子极化激元,图25(b)与图25(c)更容易看出其耦合细节.二维表面等离子极化激元根据不同掺杂而具有可调性.

图24 拓扑绝缘体的(a)双曲等频面及其(b)结构示意图[101],(b)中黄色层表示拓扑绝缘体表面态区域Fig.24.(a)Hyperboloidal isofrequency surfaces of hyperbolic phonon polaritons for two frequencies ω1and ω2(ω2＞ ω1),the asymptote angle θ with respect to the kx-kyplane is shown;the group velocity v makes the same angle with respect to the kzaxis; (b)model geometry：a topological insulator slab of thickness d sandwiched between a substrate of permittivity εsand a superstrate of permittivity ε0,the two thin(orange)layers represent the top and the bottom surfaces states[101].

图25 (a)—(c)石墨烯-六角氮化硼-石墨烯异质结构在中红外波段,以及(d)—(f)拓扑绝缘体Bi2Se3在太赫兹波段的表面声子-等离子极化激元的色散关系[101]Fig.25.Collective mode dispersions of graphene-hBN-graphene(G/hBN/G)and Bi2Se3slabs rendered using the false color maps of the imaginary part of re fl ectivity Imrp[101].The parameters of the calculation for G/hBN/G are：(a)d=60 nm,µ=0,(b)d=60 nm,µ=0.29 eV,(c)d=30 nm,µ=0.29 eV.The other parameters are v=1.00×108 cm/s,γe=1.00 THz,ε0=1,and εs=1.5.The parameters of the calculation for Bi2Se3are(d)d=120 nm,µ=0,(e)d=120 nm,µ=0.29 eV,(f)d=60 nm,µ=0.29 eV. In these three plots,v=0.623×108 cm/s,γe=1 THz,ε0=1,and εs=10.Equal doping of the top and bottom surface state is assumed.The vertical dashed lines correspond to experiments.

7.2 声学表面等离子极化激元

图21说明二维表面等离子极化激元在太赫兹波段的性能有待提升,在二维材料附近引入金属层,形成金属表面等离子极化激元与二维表面等离子极化激元相耦合的结构,从而可以将场压缩在二者所夹的中间层中,使局域性得到改善.如图26(a)所示的石墨烯/介质层/金属结构中,石墨烯中的电荷浓度以及介质层厚度均可调控耦合模的色散性能,介质层厚度越小,耦合越强,甚至使得色散曲线呈线性关系,如图26(b)中的黑色虚线所示.基于这样的特征,这种耦合模可被称为声学表面等离子极化激元[106],其特性可以通过与悬空石墨烯的二维表面等离子极化激元做对比而凸显出来.根据图27所示的2.52 THz时的近场分布计算,场被限制在42 nm厚度的六角氮化硼中,且分布均匀.这样,在z方向上场被限制到λ0/2800的区域,被约束的场强是悬空石墨烯情况下的36倍,垂直于界面的空气侧的衰减长度δd=0.26µm,远小于悬空石墨烯情况下的3.23µm,水平方向的传播波长λp≈650 nm,从而限制因子β≈183.然而,如此大的局域性基本上没有影响其低损耗特性,声学表面等离子极化激元的寿命仍在500 fs量级[106].若将图26(a)结构中的石墨烯替换为二维电子气、拓扑绝缘体等其他二维材料,其耦合效应类似.

8 结论与展望

图26 太赫兹声学表面等离子极化激元的(a)结构示意图[111]及(b)色散关系[106]Fig.26.(a)The graphene-metal plasmonic waveguide：a dielectric spacer of permittivity ε is sandwiched between metal(bottom)and graphene(top);the guided mode propagates along the x direction and exponentially decays along the z direction;a bound field distribution is represented by the red curve[111];(b)experimental and theoretical THz graphene plasmon dispersion relations;the red symbols display the experimental values;the error bars (standard deviation)are within the symbols size;the blue colour plot shows the calculated dispersion of graphene plasmons in an air/hBN/graphene/hBN/AuPd/SiO2heterostructure assuming the experimental carrier concentration and layer thicknesses;the thin blue solid line shows the calculated plasmon dispersion for free-standing graphene(air/G/air)of the same carrier concentration; the dashed black line displays the calculated plasmon dispersion,the dashed blue line indicates the light line in free space[106].

图28 表面极化激元的可能应用[55]Fig.28.Summary of the possible applications of surface polaritons[55].

太赫兹表面极化激元是克服衍射极限的太赫兹集成光子学器件的重要基础[55],如图28所示.表面声子极化激元、二维表面等离子极化激元以及混合型表面极化激元等为太赫兹亚波长器件的研制提供了物理机理.二维表面等离子极化激元因电荷浓度的改变而具有可调性;表面声子极化激元的激发、二维材料的尺寸有限化,以及层状结构设计可使电磁场的局域性变得更高;在低损耗方面,表面声子极化激元表现最佳,然而太赫兹波段响应的天然材料十分有限.基于压电/磁超构材料的太赫兹表面人工声子极化激元初现端倪[50],其工作波段可以通过结构的周期大小进行调节,其畴壁所带来的损耗特性有待进一步研究.其他利用纳米尺度的周期性缺陷来引入太赫兹声子的方法[112-122]亦值得探索,并相互借鉴.混合型表面极化激元在性能调控方面更具灵活性,可结合各类表面极化激元的优势,如表面声子-等离子极化激元可同时具备低损耗与可调性,更有实际应用前景.材料质量是确保上述物理机理发挥作用、性能得以最终实现的基石,因此在大多数情况下需要优选纯度高、缺陷少、单晶的金属、极性介电材料、半导体材料以及二维材料等,这方面可借鉴并结合纳米材料等领域的工艺与技术成果.

[1]Tonouchi M 2007 Nat.Photon.1 97

[2]Ferguson B,Zhang X C 2002 Nat.Mater.1 26

[3]Soref R 2010 Nat.Photon.4 495

[4]Mittleman D 2003 Sensing with Terahertz Radiation (Berlin：Springer)

[5]SakaiK 2005 Terahertz Optoelectronics (Berlin：Springer)

[6]Lee Y S 2009 Principles of Terahertz Science and Technology(Berlin：Springer)

[7]Zhang X C,Xu J 2010 Introduction to THz Wave Photonics(Berlin：Springer)

[8]Dhillon S S,Vitiello M S,Lin field E H,et al.2017 J. Phys.D:Appl.Phys.50 043001

[9]Fleischmann M,Hendra P J,McQuillan A J 1974 Chem. Phys.Lett.26 163

[10]Jeanmaire D L,van Duyne R P 1977 J.Electroanal. Chem.84 1

[11]Kneipp K,Wang Y,Kneipp H,Perelman L T,Itzkan I, Dasari R R,Feld M S 1997 Phys.Rev.Lett.78 1667

[12]Nie S,Emory S R 1997 Science 275 1101

[13]Li J F,Huang Y F,Ding Y,Yang Z L,Li S B,Zhou X S,Fan F R,Zhang W,Zhou Z Y,Wu D Y,Ren B, Wang Z L,Tian Z Q 2010 Nature 464 392

[14]Zhang R,Zhang Y,Dong Z C,Jiang S,Zhang C,Chen L G,Zhang L,Liao Y,Aizpurua J,Luo Y,Yang J L, Hou,J G 2013 Nature 498 82

[15]Gontijo I,Boroditsky M,Yablonovitch E,Keller S, Mishra U K,DenBaars S P 1999 Phys.Rev.B 60 11564

[16]Okamoto K,NiKi I,Shvartser A,Narukawa Y,Mukai T,Scherer A 2004 Nat.Mater.3 601

[17]Pompa P P,Martiradonna L,Della Torre A,Della Sala F,Manna L,de Vittorio M,Calabi F,Cingolani R,Rinaldi R 2006 Nat.Nanotech.1 126

[18]Shimizu K T,Woo W K,Fisher B R,Eisler H J,Bawendi M G 2002 Phys.Rev.Lett.89 117401

[19]Zhang X J,Wang P W,Zhang X Z,Xu J,Zhu Y Y,Yu D P 2009 Nano Res.2 47

[20]Zhang X J,Tang H,Huang J A,Luo L B,Zapien J A, Lee S T 2011 Nano Lett.11 4626

[21]Russell K J,Liu T L,Cui S,Hu E L 2012 Nat.Photon. 6 459

[22]Jiang J J,Xu F,Xie Y B,Tang X M,Liu Z Y,Zhang X J,Zhu Y Y 2013 Opt.Lett.38 4570

[23]Wang Z,Dong Z G,Gu Y H,Chang Y H,Zhang L,Li L J,Zhao W J,Eda G,Zhang W J,Grinblat G,Maier S A, Yang J K W,Qiu C W,Wee A T S 2016 Nat.Commun. 7 11283

[24]Genevet P,Tetienne J P,Gatzogiannis E,Blanchard R, Kats M A,Scully M O,Capasso F 2010 Nano Lett.10 4880

[25]Cai W,Vasudev A P,Brongersma M L 2011 Science 333 1720

[26]Valev V K 2012 Langmuir 28 15454

[27]Grosse N B,Heckmann J,Woggon U 2012 Phys.Rev. Lett.108 136802

[28]Li G,Zhang S,Zengtgraf T 2017 Nat.Rev.Mater.2 17010

[29]Ebbesen T W,Lezec H J,Chaemi H F,Thio T,Wol ffP A 1998 Nature 391 667

[30]Andrew P,Barnes W L 2004 Science 306 1002

[31]Atwater H A,Polman A 2010 Nat.Mater.9 205

[32]Aubry A,Lei D Y,Fernandez Dominguez A I,Sonnefraud Y,Maier S A,Pendry J B 2010 Nano Lett.10 2574

[33]Mooney J M,Silverman J 1985 IEEE Trans.Electron. Dev.32 33

[34]Clavero C 2014 Nat.Photon.8 95

[35]Sobhani A,Knight M W,Wang Y,Brown L V,Fang Z, Nordlander P,Halas N J 2013 Nat.Commun.4 1643

[36]Goykhman I,Desiatov B,Khurgin J B,Shappir J,Levy U 2011 Nano Lett.11 2219

[37]Zhang S,Genov D A,Wang Y,Liu M,Zhang X 2008 Phys.Rev.Lett.101 047401

[38]Liu N,Langguth L,Weiss T,Kästel J,Fleischhauer M, Pfau T,Giessen H 2009 Nat.Mater.8 758

[39]Brongersma M L,Kik P G 2010 Surface Plasmon Nanophotonics(New York：Springer)

[40]Oulton R F,Sorger V J,Zentgraf T,Ma R M,Gladden C,Dai L,Bartal G,Zhang X 2009 Nature 461 629

[41]Lu Y J,Kim J,Chen H Y,Wu C,Dabidian N,Sanders C E,Wang C Y,Lu M Y,Li B H,Qiu X,Chang W H, Chen L J,Shvets G,Shih C K,Gwo S 2012 Science 337 450

[42]Fang N,Lee H,Sun C,Zhang X 2005 Science 308 534

[43]Liu Z,Lee H,Xiong Y,Sun C,Zhang X 2007 Science 315 1686

[44]EnghetaN,ZiolkowskiRW 2006Metamaterials: Physics and Engineering Explorations(Hoboken,NJ：Wiley&Sons)

[45]Yu N F,Genevet P,Kats M A,Aieta F,Tetienne J P, Capasso F,Gaburro Z 2011 Science 334 333

[46]Hillenbrand R,Taubner T,Keilmann F 2002 Nature 418 159

[47]Caldwell J D,Glembocki O J,Sharac N,Giannini V, Bezares F J,Long J P,Owrutsky J C,Vurgaftman I, Tischler J G,Wheeler V D,Bassim N D,Shirey L M, Kasica R,Maier S A 2013 Nano Lett.13 3690

[48]Feurer T,Stoyanov N S,Ward D W,Vaughan J C,Statz E R,Nelson K A 2007 Ann.Rev.Mater.Res.37 317

[49]Hillenbrand R 2004 Ultramicroscopy 100 421

[50]Zhang X J,Wu D M,Sun C,Zhang X 2007 Phys.Rev. B 76 085318

[51]Huang K 1951 Proc.Roy.Soc.A 208 352

[52]Hop field J J 1958 Phys.Rev.112 1555

[53]Henry C H,Hop field JJ 1965 Phys.Rev.Lett.15 964

[54]Barnes W L,Dereux A,Ebbesen T W 2003 Nature 424 824

[55]Low T,Chaves A,Caldwell J D,Kumar A,Fang N X, Avouris P,Heinz T F,Guinea F,Martin Moreno L,Koppens F 2017 Nature Mater.16 182

[56]Kavokin A V,Shelykh I A,Malpuech G 2005 Phys.Rev. B 72 233102

[57]Kaliteevski M,Iorsh I,Brand S,Abram R A,Chamberlain J M,Kavokin A V,Shelykh I A 2007 Phys.Rev.B 76 165415

[58]Huang K 1950 Report LT 239 1

[59]Huang K 1951 Nature 167 779

[60]Born M,Huang K 1954 Dynamical Theory of Crystal Lattice(Oxford：Clarendon)

[61]Kittel C 1986 Introduction to Solid State Physics(6th Ed.)(New York：Wiley)

[62]Hook J R,Hall H E 1991 Solid State Physics(2nd Ed.) (New York：Wiley)

[63]Grosso G,Parravicini G P 2000 Solid State Physics(San Diego：Academic)

[64]Lyddane R H,Sachs R G,Teller E 1941 Phys.Rev.59 673

[65]Haraguchi M,Fukui M,Muto S 1990 Phys.Rev.B 41 1254

[66]Moore W J,Holm R T 1996 J.Appl.Phys.80 6939

[67]Yu P Y,Cardona M 1999 Fundamentals of Semiconductors:Physics and Materials Properties(New York：Springer)

[68]Passerat de Silans T,Maurin I,Chaves de Souza Segundo P,Saltiel S,Gorza M P,Ducloy M,Bloch D, Meneses D,Echegut P 2009 J.Phys.Condens.Matter 21 255902

[69]Cottam M G,Tilley D R 2004 Introduction to Surface and Superlattice Excitations(2nd Ed.)(Bristol：IOP)

[70]Auld B A 1973 Acoustic Fields and Waves in Solids (New York：Wiley)

[71]Niizeki N,Yamada T,Toyoda H 1967 Jpn.J.Appl. Phys.6 318

[72]Zhang X J,Lu Y Q,Zhu Y Y,Chen Y F,Zhu S N 2004 Appl.Phys.Lett.85 3531

[73]Lu Y Q,Zhu Y Y,Chen Y F,Zhu S N,Ming N B,Feng Y J 1999 Science 284 1822

[74]Zhu Y Y,Zhang X J,Lu Y Q,Chen Y F,Zhu S N,Ming N B 2003 Phys.Rev.Lett.90 053903

[75]Zhang X J,Xuan X F,Lu Y Q,Zhu Y Y,Chen Y F, Zhu S N,Ming N B 2003 Physics 32 745

[76]Zhang X J,Zhu R Q,Zhao J,Chen Y F,Zhu Y Y 2004 Phys.Rev.B 69 085118

[77]Caldwell J D,Lindsay L,Giannini V,Vurgaftman I,Reinecke T L,Maier S A,Glembocki O J 2015 Nanophotonics 4 44

[78]Hu X K,Ming Y,Zhang X J,Lu Y Q,Zhu Y Y 2012 Appl.Phys.Lett.101 151109

[79]Williams C R,Andrews S R,Maier S A,Fernández Domínguez A I,Martín Moreno L,García Vidal F J 2008 Nat.Photon.2 175

[80]Pendry J B,Martín Moreno L,García Vidal F J 2004 Science 305 847

[81]García Vidal F J,Martín Moreno L,Pendry J B 2005 J. Opt.A:Pure Appl.Opt.7 S97

[82]Hibbins A P,Evans B R,Sambles J R 2005 Science 308 670

[83]Maier S A,Andrews S R,Martín Moreno L,García Vidal F J 2006 Phys.Rev.Lett.97 176805

[84]van Exter M,Grischkowsky D 1990 Phys.Rev.B 41 12140

[85]Saxler J,Gómez Rivas J,Janke C,Pellemans H P M, Haring Bolivar P,Kurz H 2004 Phys.Rev.B 69 155427

[86]Gómez Rivas J,Kuttge M,Haring Bolivar P,Kurz H, Sánchez Gil J A 2004 Phys.Rev.Lett.93 256804

[87]Ashcroft N W,Mermin N D 1976 Solid State Physics (Philadelphia,PA：Saunders)

[88]Allen Jr S J,Tsui D C,Logan R A 1977 Phys.Rev.Lett. 38 980

[89]Stern F 1967 Phys.Rev.Lett.18 546

[90]Nakayama M 1974 J.Phys.Soc.Jpn.36 393

[91]Basov D N,Fogler M M,García de Abajo F J 2016 Science 354 195

[92]Castro Neto A H,Guinea F,Peres N M R,Novoselov K S,Geim A K 2009 Rev.Mod.Phys.81 109

[93]Liu Y,Willis R F,Emtsev K V,Seyller T 2008 Phys. Rev.B 78 201403

[94]Falkovsky L A 2008 J.Phys.:Conf.Ser.129 012004

[95]Wang W H,Apell P,Kinaret J 2011 Phys.Rev.B 84 085423

[96]Nikitin A Y,Guinea F,García Vidal F J,Martín Moreno L 2011 Phys.Rev.B 84 161407

[97]Zhu X L,Yan W,Asger Mortensen N,Xiao S S 2013 Opt.Express 21 3486

[98]Zhang H J,Liu C X,Qi X L,Dai X,Fang Z,Zhang S C 2009 Nat.Phys.5 438

[99]Di Pietro P,Ortolani M,Limaj O,Di Gaspare A,Giliberti V,Giorgianni F,Brahlek M,Bansal N,Koirala N, Oh S,Calvani P,Lupi S 2013 Nat.Nanotech.8 556

[100]Poddubny A,Iorsh I,Belov P,Kivshar Y 2013 Nat.Photon.7 948

[101]Wu J S,Basov D N,Fogler M M 2015 Phys.Rev.B 92 205430

[102]Bohren C F,Hu ff man D R 2004 Absorption and Scattering of Light by Small Particles(Weinheim：John Wiley &Sons)

[103]Scharte M,Porath R,Ohms T,Aeschlimann M,Krenn J R,Ditlbacher H,Aussenegg F R,Liebsch A 2001 Appl. Phys.B 73 305

[104]Kreibig U,Vollmer M 2010 Optical Properties of Metal Clusters(Berlin：Springer)

[105]Bosman M,Ye E,Tan S F,Nijhuis C A,Yang J K W, Marty R,Mlayah A,Arbouet A,Girard C,Han M Y 2013 Sci.Rep.3 1312

[106]Alonso Gonzalez P,Nikitin A Y,Gao Y,Woessner A, Lundeberg M B,Principi A,Forcellini N,Yan W,Vélez S,Huber A J,Watanabe K,Taniguchi T,Casanova F, Hueso L E,Polini M,Hone J,Koppens F H L,Hillenbrand R 2017 Nat.Nanotech.12 31

[107]Nagpal P,Lindquist N C,Oh S H,Norris D J 2009 Science 325 594

[108]Kariniemi M,Niinisto J,Hatanpaa T,Kemell M,Sajavaara T,Ritala M,Leskelä M 2011 Chem.Mater.23 2901

[109]Wang C Y,Chen H Y,Sun L Y,Chen W L,Chang Y M,Ahn H,Li X Q,Gwo S 2015 Nat.Commun.6 7734

[110]Liang H Z,Kim D J,Chung H S,Zhang J,Yu K N,Li S H,Li R X 2003 Acta Phys.Chim.Sin.19 150

[111]Gu X F,Lin I T,Liu J M 2013 Appl.Phys.Lett.103 071103

[112]Sridhara S G,Carlsson F H C,Bergman J P,Janzen E 2001 Appl.Phys.Lett.79 3944

[113]Stahlbush R E,Fatemi M,Fedison J B,Arthur S D, Rowland L B,Wang S 2002 J.Electron.Mater.31 370

[114]Caldwell J D,Klein P B,Twigg M E,Stahlbush R E 2006 Appl.Phys.Lett.89 103519

[115]Caldwell J D,Liu K X,Tadjer M J,Glembocki O J, Stahlbush R E,Hobart K D,Kub F 2007 J.Electron. Mater.36 318

[116]Caldwell J D,Stahlbush R E,Glembocki O J,Ancona M G,Hobart K D 2010 J.Appl.Phys.108 044503

[117]Caldwell J D,Stahlbush R E,Hobart K D,Glembocki O J,Liu K X 2007 Appl.Phys.Lett.90 143519

[118]Galeckas A,Linnros J,Pirouz P 2006 Phys.Rev.Lett. 96 025502

[119]Ha S,Skowronski M,Sumakeris J J,Paisley M J,Das M K 2004 Phys.Rev.Lett.92 175504

[120]Iwata H P,Lindefelt U,Oberg S,Briddon P R 2003 Physica B 340 165

[121]Maximenko S I,Freitas J A,Klein P B,Shrivastava A, Sudarshan T S 2009 Appl.Phys.Lett.94 092101

[122]Bergman J P,Lendenmann H,Nilsson P A,Lindefelt U, Skytt P 2001 Mater.Sci.Forum 353–356 299

PACS:87.50.U—,71.36.+c,61.48.Gh,78.67.Pt DOI:10.7498/aps.66.148705

Terahertz surface polaritons∗

Zhang Xue-Jin†Lu Yan-Qing Chen Yan-Feng Zhu Yong-Yuan Zhu Shi-Ning
(Collaborative Innovation Center of Advanced Microstructures,National Laboratory of Solid State Microstructures,College of Engineering and Applied Sciences,Nanjing University,Nanjing 210093,China)

28 June 2017;revised manuscript

13 July 2017)

Enormous e ff orts have been made to manipulate the light-matter interactions,especially in sub-di ff raction-limited space,leading to miniaturized and integrated photonic devices.In physics,an elementary excitation,called polariton, which is the quantum of the coupled photon and polar elementary excitation wave field,underlies the light-matter interaction.In the dispersion relation,polaritons behave as anti-crossing interacting resonance.Surface polaritons provide ultra-con fi nement of electromagnetic field at the interface,opening up possibilities for sub-di ff raction-limited devices,and various field enhancement e ff ects.In the electromagnetic spectra,terahertz(THz)regime was called THz gap before the 1990s,but has now been thrust into the limelight with great signi fi cance.This review is devoted to the emerging but rapidly developing field of sub-di ff raction-limited THz photonics,with an emphasis on the materials and the physics of surface polaritons.A large breadth of di ff erent fl avours of materials and surface polaritonic modes have been summarized.The former includes metallic,dielectric,semiconductor,two-dimensional(2D)materials,metamaterials, etc.;the latter covers surface phonon-,plasmon-,and hybrid polaritons.In the THz regime,2D surface plasmon polariton and arti fi cial surface phonon polaritons o ff er more attractive advantages in ability to obtain low-loss,tunable, ultracompact light-matter modes.

terahertz,surface polaritons,two-dimensional materials,near- field optics

:87.50.U—,71.36.+c,61.48.Gh,78.67.Pt

10.7498/aps.66.148705

∗国家重点研发计划(批准号：2017YFA0303700)和国家自然科学基金(批准号：11621091,11374150,11274159)资助的课题.

†通信作者.E-mail：xuejinzh@nju.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Key Research and Development Program of China(Grant No.2017YFA0303700)and the National Natural Science Foundation of China(Grant Nos.11621091,11374150,11274159).

†Corresponding author.E-mail：xuejinzh@nju.edu.cn