X形超阻尼局域共振声子晶体梁弯曲振动带隙特性∗

杜春阳 郁殿龙刘江伟 温激鸿

(国防科学技术大学,装备综合保障技术重点实验室,长沙 410073)

X形超阻尼局域共振声子晶体梁弯曲振动带隙特性∗

杜春阳 郁殿龙†刘江伟 温激鸿

(国防科学技术大学,装备综合保障技术重点实验室,长沙 410073)

(2017年3月7日收到;2017年4月19日收到修改稿)

以声子晶体理论为基础,设计了一种具有超阻尼特性的X形局域共振结构,分析了周期性附加X形局域共振的梁弯曲振动传播特性.利用拉格朗日方程分析了X形局域共振结构动力学等效特性,揭示了该结构的阻尼放大的机理,分析了几何结构参数对于带隙特性的影响,并利用有限元法验证了X形局域共振结构的超阻尼特性.研究结果表明,周期性附加X形局域结构能够有效地抑制低频弯曲振动在梁中的传播,产生超阻尼特性,实现低频、宽带的减振效果,为结构的低频减振提供了一个新的设计方案.

声子晶体,带隙,超阻尼,几何非线性

1 引 言

振动是一种普遍的物理现象,由于振动或冲击而产生的共振、疲劳破坏等危害到国民经济的各个领域,如航空航天、仪器仪表、机械动力、交通运输以及军事国防工业等[1].而且随着科学技术和国民经济的日益发展,对产品结构抗振性能提出了越来越高的要求[2].

近年来凝聚态物理领域声子晶体理论的兴起,为振动的控制提供了一种新的思路[3,4].周期性结构的带隙特性已经有了较为广泛的发展：2014年,舒海生等[5]针对工程常用多杆结构,构造一类布拉格声子晶体T形杆,拓宽了减振频带,获得了良好的振动衰减效果;2017年,Ma等[6]基于三维各向异性局域共振振子,设计了一种内嵌式的超材料,并通过实验证明该结构可以选择性的对各类振动进行抑制,开创了弹性波分离控制的新方法;2000年,Liu等[7]首次提出了局域共振型声子晶体概念,由于局域共振声子晶体具有“小尺寸控制大波长”的特点,因而局域共振声子晶体在低频减振降噪中具有广泛的应用前景.如何设计局域共振结构目前已经得到高度关注;2013年,吴九汇等[8]设计了一种新型的螺旋局域共振单元声子晶体板结构,并结合数值计算和试验验证了其良好的低频振动带隙特性;2016年,张印等[9]针对低频结构振动控制,设计了一种质量放大局域共振型声子晶体并通过实验验证了对低频减振的良好效果;2016年,张佳龙等[10]提出了一种双包覆层局域共振声子晶体结构;同年,祁鹏山等[11]提出了一种四角连接局域共振声子晶体;陈琳等[12]设计了一种基于局域共振机理的带瓣型结构的声学超材料.随着超材料概念的发展,一些新的超常物理特性得到关注,如超阻尼现象.2013年,Hussein和Frazier[13]通过对弹簧质量链超材料的研究提出了阻尼产生现象,为设计具有高阻尼、高刚度的结构提出了一种新思路. 2015年,Nouh等[14]通过理论与实验验证了添加周期局域共振振子板的超阻尼现象.2015年,Frazier和Hussein[15]通过引入黏弹性阻尼对于弹簧质量链结构进行分析,进一步揭示了该系统超阻尼现象的机理.但是这种超阻尼现象主要是局域共振声子晶体比布拉格声子晶体阻尼增强,超阻尼局域共振结构设计研究相对较少.

非线性减振理论也得到了深入研究,X形隔振器具有非线性等特点,能够产生较好的非线性刚度与阻尼,因而得到广泛关注.在20世纪90年代,汽车工程首次采用了斜支承弹簧几何非线性减振系统,其减振效果优于弹簧线性减振系统的减振效果.1997年,吴强等[16]利用有限元法研究了小应变中转动几何非线性情况下黏弹性材料梁的振动响应问题.2008年,吴晓和杨立军[17]分析了悬挂弹簧几何非线性减振系统的固有振动特性,通过改变弹簧倾斜角,使悬挂弹簧系统处于软弹簧特性区域来进行减振.2015年,Liu等[18]设计了一种X形结构的减振器,并从理论上分析了其相对于经典结构的优点,指出X形结构存在几何非线性,相比于经典的弹簧振子结构,具有非线性刚度和阻尼的特点,振动衰减效应更佳.2015年,Sun和Jing[19]从几何非线性出发,设计具有非线性刚度、阻尼和摩擦力的剪刀型隔振器,从理论层面分析了其良好的隔振性能,并于2016年对剪刀型隔振器进行了进一步改善并进行了实验验证[20].

为了实现低频、宽带减振效果,提高结构的阻尼特性,本文结合声子晶体理论和X形结构特点,设计了一种具有超阻尼特性的X形局域共振结构,并分析其弯曲振动带隙特性及减振特性.

2 X形局域共振结构动力学建模

图1(a)所示为无限周期结构示意图,在基体梁上周期性地挂接X形局域共振结构形成声子晶体梁,单元的尺寸即晶格常数为a.图1(b)为单个周期结构示意图,在梁单元上挂接X形局域共振结构,X形局域共振结构的主要框架由四根长度为l0的轻质杆件构成,杆件依次连接.在四个节点I,II, III,IV处,杆件只能以节点为中心绕z轴进行旋转.弹簧的刚度为k2,挂接在I,III两个节点上.II,IV两个节点处分别挂接两个质量为m/2的质量块.θ是初始状态下轻质杆与水平方向的夹角.

图1 周期附加X形结构的局域共振梁结构示意图 (a)无限周期结构;(b)单元结构Fig.1.The sketch of local resonance beam with periodic X-shape structure：(a)In fi nite period structure;(b)local resonance unit.

2.1 X形局域共振结构动力学等效

简化模型如图2所示,其中m/2是振子质量, k2是弹簧的刚度,u1是质量块的位移,u2是节点的位移,l0是轻质杆的杆长,θ是初始时刻轻质杆与水平方向的夹角.

由几何关系可知,X形局域共振结构运动的变形可由角度φ和u1方向位移表示[21]：

其中φ是运动过程中X形局域共振结构轻质杆与水平夹角的变形,假设质量在小位移下只考虑在水平方向上的位移,可以确定振子的能量方程：

利用拉格朗日方程,对系统的动力学方程进行求解,施加力为保守力,方程形式为[22]

图2 X形局域共振结构单元动力学模型Fig.2.The dynamic model of X-shape structure.

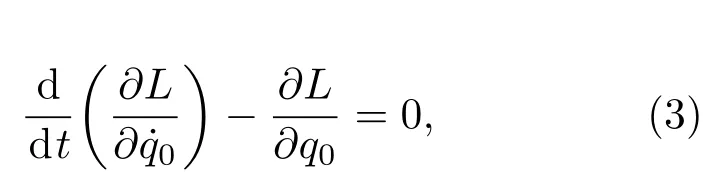
其中L=T-V是拉格朗日函数,q0为广义坐标.

选择下节点的位移u2作为广义坐标.拉格朗日函数为将(1)式几何关系代入拉格朗日函数中：

若不考虑整个系统阻尼,令

则系统的振动微分方程

通过对公式结构的线性化处理,取一阶泰勒展开,则系统的振动微分方程

在弹簧没有添加阻尼的情况下,系统出现了等效阻尼,附加的等效阻尼是由几何非线性引起的,与结构参数以及位移相关.f(u2)是属于一个非线性变化的函数,在附加结构的运动过程中,结构的动力学微分方程中的等效质量和阻尼项的形式是不断变化的.但是在整个系统中不存在实际阻尼,不产生能量耗散,附加等效阻尼与两质量块的运动相关,本质上属于质量块将系统的振动进行了吸收,而在进行结构等效时,产生了类似于阻尼产生的效果.这与Manimala等[23]得出的阻尼产生结果类似,因而说明X形局域共振结构能够改善系统的阻尼特性.

若考虑弹簧阻尼,即在弹簧中加入相应的阻尼条件,假设阻尼因子为η,则系统在运动过程中的耗能为[24]

其中,v是固有运动速度,u是运动位移.

q0为广义坐标.将(9)式代入(8)式得

由于在本结构中,广义坐标为u2,则耗散函数为

将其代入带耗散函数的拉格朗日方程中,

则振子运动微分方程为

2.2 传递矩阵法求解局域共振型周期结构梁

传统的局域共振型周期梁是在基体梁上直接附加橡胶与质量块,故可近似看为弹簧质量振子模型,可采用传递矩阵法求解其能带结构.由于本文涉及的梁轴向尺寸远大于截面形状尺寸,故采用欧拉-伯努利梁模型[25]：

其中ρ,E分别为密度、弹性模量;A为梁的截面面积;I为截面二次矩;梁的横向位移为y(x,t).设位移y(x,t)=X(x)exp(iωt),其中ω为角频率.

利用传递矩阵法可以得到[26,27]

其中ψn为状态矢量,T为局域共振梁传递矩阵,由于结构的周期性,矢量ψn满足Bloch定理,即得到标准的特征值

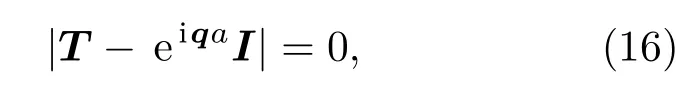
其中q为Bloch波矢,a为晶格常数.

通过求解矩阵T的特征值,即可求得无限周期结构中的角频率ω和波矢q,也即色散关系曲线.当频率位于某些范围时,将无法求得与之对应的实数q值,也即周期结构中这些频率范围内的弹性波将不存在稳定的传播模式.

2.3 多体动力学的有限元建模

有限元法目前被广泛应用于工程领域,是一种强有力的数值计算方法.有限元法分析的实质是最小势能原理的应用,其核心在于把无限个自由度的连续系统理想化为有限个自由度的单元集合体,进而使用离散的方式组合表达全几何场上的形函数而不是直接寻找全场上的形函数.

梁有限元动力方程为

其中,M为单元质量矩阵,C为单元阻尼矩阵,K为单元刚度矩阵.

不考虑阻尼的影响,(17)式可以写作[28]

则元胞边界处左端和右端的方程可写成

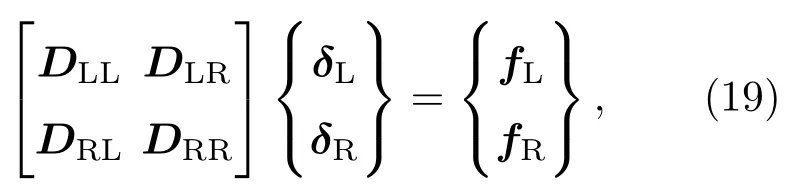
式中,D=K-ω2M为动刚度矩阵.由Bloch定理可得到周期边界条件：

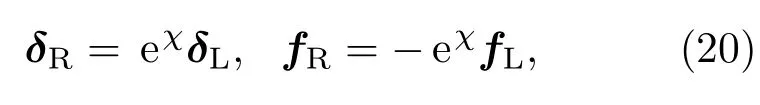
χ为传播常数,其包含信息有Bloch波矢q及晶格常数a.

可以转化为标准特征值问题：

进一步,通过求解矩阵T的特征值,即可得到Bloch波矢与频率的关系,

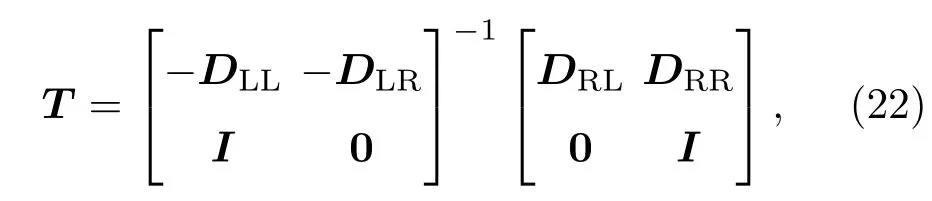
通过求解,可以获得相应的固有频率和振型.

ComsolMultiphysics是Comsol集团开发的有限元仿真软件,可通过附加力载荷等激励信号来计算分析模型的特性.利用Comsol对X形局域共振结构进行建模仿真,由于需要保证节点处的旋转要求,简单的弹性体建模只是两种材料的连接,并不能达到要求.故采用多体动力学进行建模,图3所示为X形局域共振结构在Comsol中的单元仿真模型,利用橡胶条模拟弹簧.为了满足旋转的自由度,杆件之间的连接采用刚体铰链,除去四个刚性铰链,结构的其余部分仍采用弹性体材料进行建模.不仅保证了结构所要求的旋转自由度,更极大程度地模拟了现实的结构的材料属性.

图3 X形局域共振结构单元仿真模型图Fig.3.The simulation model of X-shape structure.

由于是周期结构,故其中场的本征频率和本征模式具有一定的对称性,所以在研究其本征场时可以将问题进行相应的简化.利用Bloch定理,元胞的边界位移和力向量关系满足[4]

计算无限周期结构能带曲线时,通过线性拉伸与Bloch定理设置结构周期性边界条件.进而可以求解无限周期的结构能带曲线[29-31].同时,将结构周期拓展为6个,如图1(a)所示.分别定义每个周期单元的铰链,在有限周期结构的基体梁一端施加位移或者力激励,在另一端拾取相应的信号数据,可以计算有限周期结构的频率响应.

3 无阻尼声子晶体梁带隙特性

3.1 带隙计算

首先,不考虑弹簧阻尼特性,利用Comsol建立图3所示的模型,计算中基体梁材料为铝,弹簧材料为橡胶,质量为铜,其结构参数与材料参数列于表1和表2.

表1 X形局域共振梁结构参数Table 1.Structural parameters of beam with periodic X-shape structure.

计算X形局域共振梁的能带结构与弯曲振动传输特性曲线,选择6个结构单元,在基体梁的一端添加弯曲的点激励,在梁的另一段拾取信号,通过对两个信号的处理,获得弯曲振动传输特性曲线(frequency response function,FRF),如图4所示.

其中60—100 Hz,167—194 Hz位置出现弯曲振动带隙,分别为布拉格带隙与局域共振带隙.而本文主要研究局域共振带隙,且60—100 Hz的布拉格带隙振动衰减较小,故后文中将不再对其进行描述.

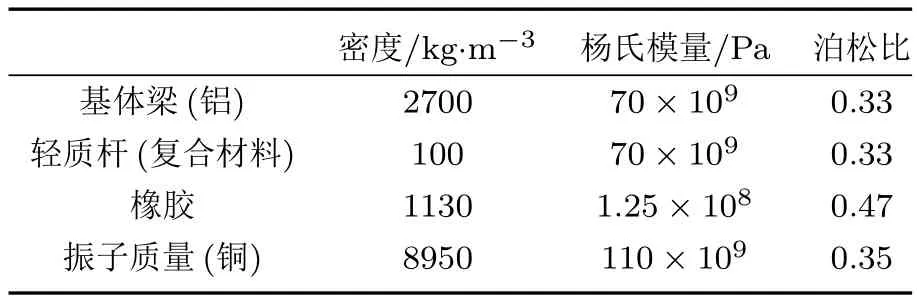
表2 X形局域共振梁材料参数Table 2.Material parameters of beam with periodic X-shape structure.

由于结构涉及多体动力学范畴,所以结构的波动模式较多.为了验证弯曲振动带隙,我们分析局域共振结构单元的振型.起始与截止频率的振型如图5所示,起始频率处主要是振子进行振动,基体梁几乎不发生任何变形;截止频率处,基体梁和振子振动且方向相反.可以判断该带隙是典型的局域共振带隙.

图4 X形局域共振梁弯曲振动带隙特性 (a)能带结构曲线;(b)弯曲振动传输曲线Fig.4.The fl exural vibration band gap characteristics of beam with periodic X-shape structure：(a)Band structure of in fi nitely periodic beam;(b)FRF of fi nitely periodic beam.

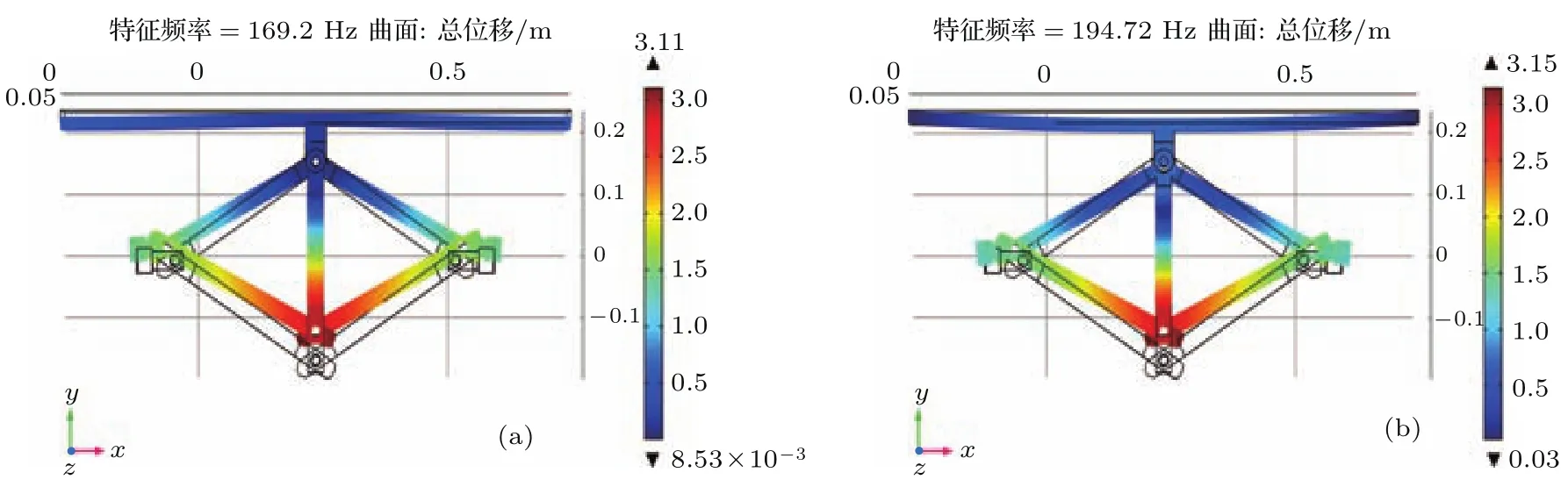
图5 周期附加X形结构局域共振梁振型 (a)169 Hz;(b)194 HzFig.5.Model shapes of beam with periodic X-shape structure：(a)169 Hz;(b)194 Hz.

图6 等效局域共振梁带隙特性 (a)能带结构曲线;(b)弯曲振动传输曲线Fig.6.The fl exural vibration band gap characteristics of classic local resonance beam with equivalent mass and sti ff ness：(a)Band structure of in fi nitely periodic beam;(b)FRF of fi nitely periodic beam.

根据上文分析,获得了X形局域共振结构的振动运动方程,通过结构等效,可以将其看作为一个质量弹簧局域共振梁结构.由于计算是在固体力学范畴,所以假设均为小变形,结构不加阻尼,对(7)式进行简化,将公式前两项进行处理,等效后结构振子运动方程为

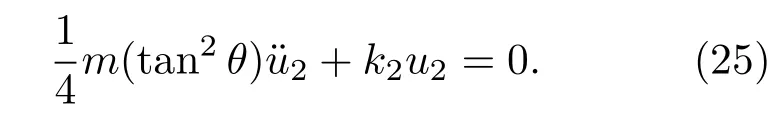
相关结构与材料参数与表1和表2一致,利用传递矩阵法进行计算,振子等效质量为弹簧的刚度为k2.求解相应的能带结构与弯曲振动传输特性曲线,如图6所示.

由图6可知,在150 Hz的位置存在一个局域共振带隙,但是,在参数一致的情况下,与含X形结构的局域共振梁相比,虽然带隙存在的位置一致,但是带隙的宽度却出现了较为明显的缩减,由于X形局域共振结构中几何非线性的存在,使得系统出现了附加阻尼,带隙宽度出现了较大程度的拓宽.

3.2 X形局域共振结构参数对带隙特性的影响规律

由(7)式可知,振子的运动方程与结构的夹角和杆长相关,所以X形局域共振结构的带隙特性与夹角和杆长相关.改变X形局域共振结构的结构参数,计算相应的弯曲振动传输特性曲线,讨论其对系统带隙特性的影响.

1)夹角θ的影响

这里,仅改变结构轻质杆与水平角度的夹角,但保持刚度不变.改变X形局域共振结构的杆件之间的夹角分别为θ=40°,θ=45°,对三种夹角的X形局域共振结构进行弯曲振动传输特性曲线计算,如图7所示.

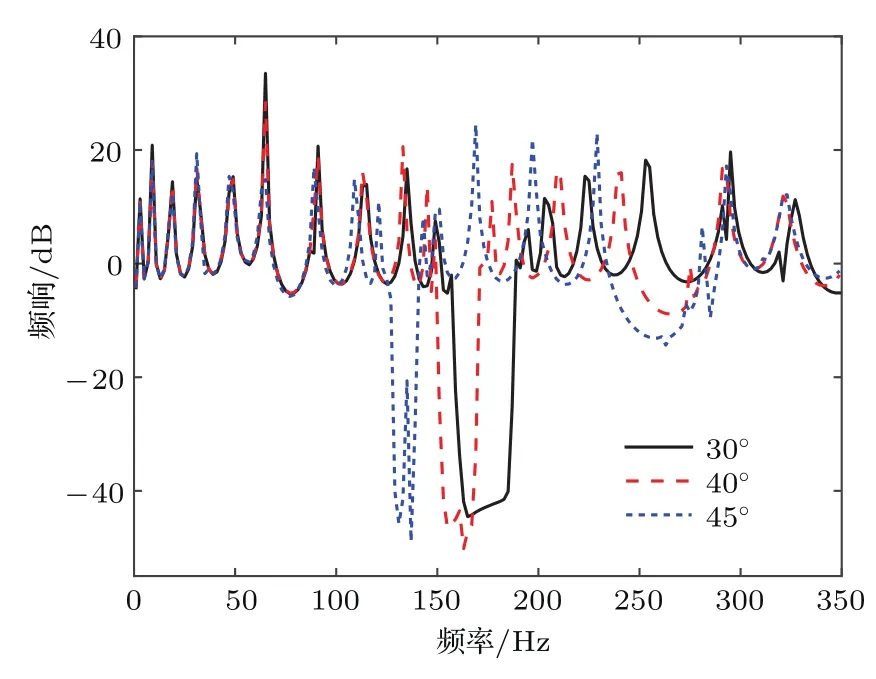
图7 不同角度下弯曲振动频率响应特性比较Fig.7.FRF of fi nitely beam with periodic X-shape structure of three di ff erent θ.

随着角度的增加,结构的等效附加质量增加,带隙频率向低频偏移.而(7)式中第二项的阻尼因素与角度和杆长相关,随角度的变化,阻尼影响结构带隙特性,使得带隙的宽度出现明显的变化.

2)轻质杆长l0的影响

取为l0=0.35 m,l0=0.5 m,保持等效刚度不变.对三种杆长的X形局域共振结构进行弯曲振动传输特性曲线计算,如图8所示.

改变X形局域共振结构轻质杆长,带隙特性基本不发生变化,可知轻质杆长对于结构的影响较小,故可以在保持结构带隙特性条件下将结构小型化.

图8 不同杆长弯曲振动频率响应特性比较Fig.8.FRF of fi nitely beam with periodic X-shape structure of three di ff erent l0.

4 阻尼声子晶体梁带隙特性

进一步,考虑X形局域共振结构中的弹簧具有阻尼因子的情况.此时,通过计算弯曲振动频率响应来描述带隙特性.通过Comsol有限元建模,在多体动力学物理场下,仅对模拟弹簧的橡胶条添加各向同性损耗因子,与不添加各向同性损耗因子的X形局域共振结构弯曲振动曲线进行比较,令X形结构中橡胶条各向同性损耗因子为η1,如图9所示.

图9(a)和图9(b)分别是添加0.1,0.2各向同性损耗因子的弯曲传输特性曲线与不添加各向同性损耗因子X形局域共振结构梁的比较,当添加阻尼因素后,结构的带隙特性出现较大的改善,带隙拓宽比较明显.当同性损耗因子增加至0.5时,如图9(c)所示,其带隙宽度几乎拓宽了一倍,大幅增强了结构的低频减振效果.

为了比较分析,建立弹簧质量等效结构的物理模型,其中,弹簧利用橡胶代替,建模时保持质量与刚度大小一致.同样向等效结构的橡胶中添加各向同性损耗因子,计算其弯曲振动传输特性曲线,令等效结构中各向同性损耗因子为η2,如图10所示.

图9 含阻尼X形局域结构弯曲振动传输特性曲线 (a)η1=0.1;(b)η1=0.2;(c)η1=0.5Fig.9.FRF of fi nitely beam with periodic X-shape structure of di ff erent Isotropic loss factor：(a)η1=0.1; (b)η1=0.2;(c)η1=0.5.

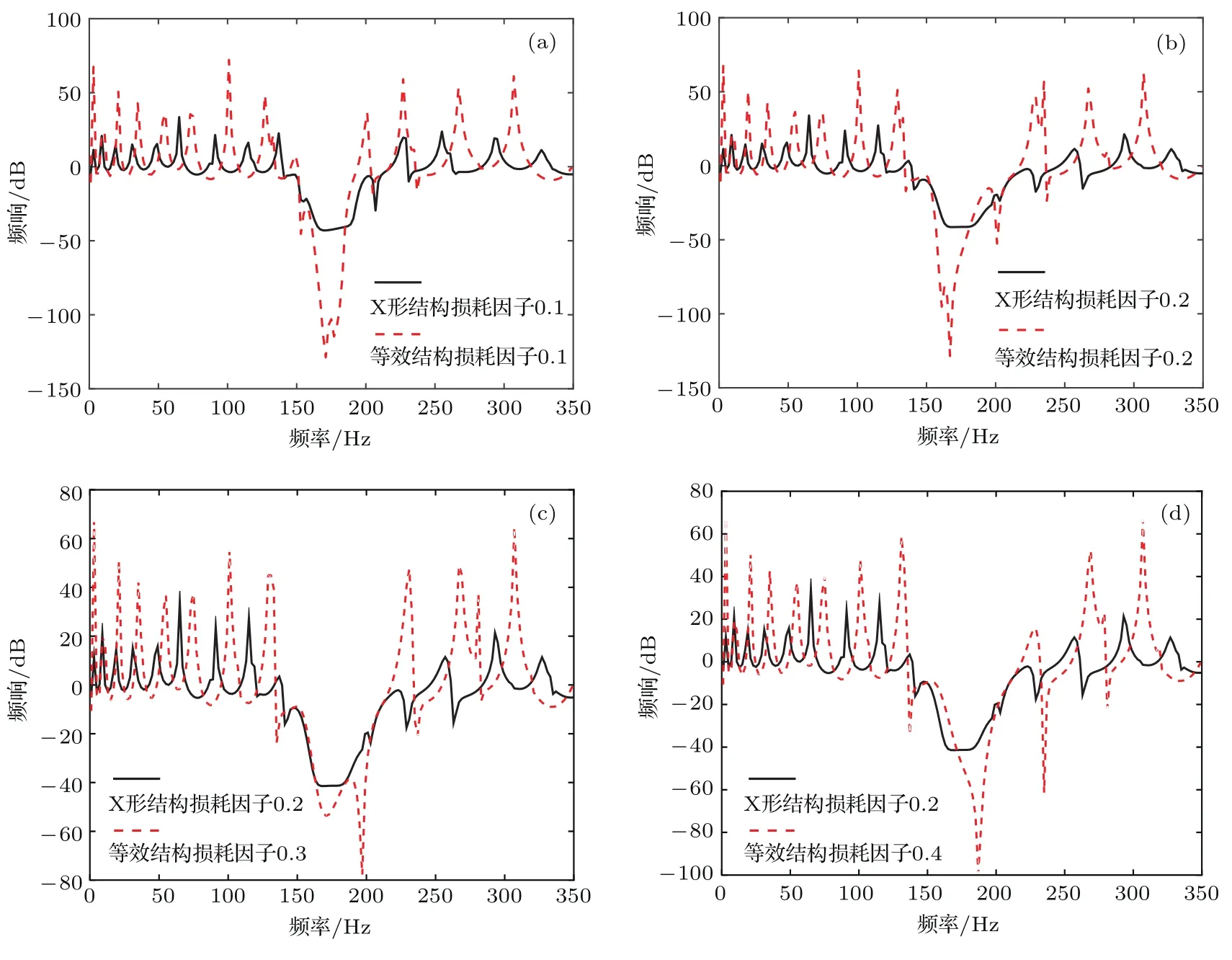
图10 添加不同各向同性损耗因子条件下X形局域共振结构和经典局域共振结构梁弯曲振动传输特性曲线比较 (a)η1=η2= 0.1;(b)η1=η2=0.2;(c)η1=0.2, η2=0.3;(d)η1=0.2, η2=0.4Fig.10.With di ff erent isotropic loss factor,the comparison of FRF of fi nitely beam with periodic X-shape structure and fi nitely classic local resonance periodic beam：(a)η1= η2=0.1;(b)η1= η2=0.2;(c)η1=0.2, η2=0.3; (d)η1=0.2, η2=0.4.

图10(a)和图10(b)是各向同性损耗因子分别为0.1,0.2时,周期附加X形局域共振结构梁和周期附加等效弹簧质量局域共振结构梁弯曲传输特性曲线的比较.损耗因子为0.1时,X形局域共振结构梁带隙较等效结构梁有一定的拓宽,且弯曲振动的峰值有较为明显的降低.损耗因子为0.2时,X形局域共振结构梁带隙宽度明显宽于等效结构梁,并且大幅度地降低了弯曲振动通带频率范围内的振动响应峰值.

图10(c)和图10(d)是X形局域共振结构中添加各向同性损耗因子为0.2、等效弹簧质量局域共振梁各向同性损耗因子分别为0.3和0.4时弯曲传输特性曲线的比较.与等效结构相比,即使各向同性损耗因子较小,X形局域共振结构梁的带隙仍较宽,且通带频率范围内振动响应值更低.所以X形局域共振结构能够明显“放大”系统的阻尼特性,达到更好的减振效果.

根据(13)式和仿真结果分析,X形局域共振结构能够显著增强系统的阻尼特性,当阻尼较小时, X形局域共振结构能够产生较为明显的阻尼“放大”效果,证明了X形局域共振结构中存在的超阻尼现象.

5 结 论

本文基于声子晶体理论和非线性X形结构,设计了一种X形局域共振结构,分析了周期附加X形局域共振结构的梁弯曲振动带隙特性.研究结论如下：

1)利用拉格朗日方程,建立了X形局域共振结构动力学模型,揭示了几何非线性对结构等效质量和等效阻尼的影响,揭示了该结构的阻尼机理,该结构可以显著增强系统阻尼,改善带隙特性;建立了多体动力学带隙计算方法,实现X形局域共振的能带结构与传输特性计算;

2)对于无阻尼系统,X形局域共振结构由于其几何非线性,带来非线性变化的等效质量,实现随位移等参数变化的等效阻尼,拓宽了周期结构的带隙频率范围;通过对结构带隙影响规律的分析,发现夹角θ对带隙影响较大,轻质杆长l0影响较小;

3)对于有阻尼系统,X形局域共振结构能够有效地‘放大’阻尼特性,进一步改善结构的带隙特性;与等效结构相比,在同样阻尼大小条件下,X形局域共振结构不仅能获得更宽的带隙,还能较大程度地抑制通带频率范围内的振动峰值,减振效果更佳.

总之,通过对X形局域共振结构的研究,验证了其具有几何非线性和良好的超阻尼特性,能够有效地拓宽低频带隙,降低振动峰值,在低频、宽带减振设计中具有一定应用前景.

[1]Ding W J 2014 Damping Theory(Beijing：Tsinghua Press)pp1–4(in Chinese)[丁文镜2014减振理论(北京：清华大学出版社)第1—4页]

[2]Silva C W(translated by Li H B,Zhang M)2013 Vibration Damping,Control and Design(Beijing：Mechanical Industry Press)pp243–246(in Chinese)[Silva C W著(李惠彬,张曼译)2013振动阻尼、控制和设计(北京：机械工业出版社)第243—246页]

[3]WenX S2006TheoryandTechnologyofPhotonic/Phononic Crystals(Beijing：Science Press)pp5–7 (in Chinese)[温熙森2006光子/声子晶体理论与技术(北京：科学出版社)第5—7页]

[4]Wen X S,Wen J H,Yu D L,et al.2009 Photonic Crystal (Beijing：National Defence Industry Press)pp8–10(in Chinese)[温熙森,温激鸿,郁殿龙等2009声子晶体(北京：国防工业出版社)第8—10页]

[5]Shu H S,Zhang F,Liu S G,Gao E W,Li S D 2014 J. Vib.Shock 33 147(in Chinese)[舒海生,张法,刘少刚,高恩武,李世丹2014振动与冲击33 147]

[6]Ma G C,Fu C X,Wang G H,Hougne del P,Christensen J,Lai Y,Sheng P 2016 Nat.Commun.7 13536

[7]Liu Z,Zhang X,Mao Y,Zhu Y Y,Yang Z,Chan C T, Sheng P 2000 Science 289 1734

[8]Wu J H,Zhang S W,Shen L 2013 Chin.J.Mech.49 62 (in Chinese)[吴九汇,张思文,沈礼2013机械工程学报49 62]

[9]Zhang Y,Yin J F,Wen J H,Yu D L 2016 J.Vib.Shock 35 26(in Chinese)[张印,尹剑飞,温激鸿,郁殿龙2016振动与冲击35 26]

[10]Zhang J L,Yao H,Du J,Zhao J B,Dong Y K 2016 Bull. Chin.Ceram.Soc.35 2767(in Chinese)[张佳龙,姚宏,杜军,赵静波,董亚科2016硅酸盐通报35 2767]

[11]Qi P S,Du J,Jiang J L,Dong Y K,Zhang J L 2016 J. Synthetic Cryst.45 1094(in Chinese)[祁鹏山,杜军,姜久龙,董亚科,张佳龙2016人工晶体学报45 1094]

[12]Chen L,Wu W G,Zhou R 2016 Tech.Acoust.35 222 (in Chinese)[陈琳,吴卫国,周榕2016声学技术35 222]

[13]Hussein M I,Frazier M J 2013 J.Sound Vib.332 4767

[14]Nouh M,Aldraihen O,Baz A 2015 J.Sound Vib.341 53

[15]Frazier M J,Hussein M I 2015 J.Acoust.Soc.Am.138 3169

[16]Wu Q,Ling D S,Xu X 1997 J.Zhejiang Univ.-Sci.A 4 462(in Chinese)[吴强,凌道盛,徐兴1997浙江大学学报4 462]

[17]Wu X,Yang L J 2008 J.Vib.Shock 2 771(in Chinese) [吴晓,杨立军2008振动与冲击2 771]

[18]Liu C C,Jing X J,Li F M 2015 Int.J.Mech.Sci.98 169

[19]Sun X T,Jing X J 2015 Mech.Syst.Signal Pr.62 149

[20]Sun X T,Jing X J 2016 Mech.Syst.Signal Pr.80 166

[21]Sun X T,Jing X J,Xu J,Cheng L 2014 J.Sound Vib. 333 2404

[22]Huang Y Y,Zhao Y G,Zhao W D 2011 J.Qinghai Univ. 2 912(in Chinese)[黄永玉,赵永刚,赵伟东2011青海大学学报2 912]

[23]Manimala J M,Huang H H,Sun C T,Snyder R,Bland S 2014 Eng.Struct.80 458

[24]Wang Z F 2001 J.Shandong Univ.Technol.1 51(in Chinese)[王振发2001齐鲁工业大学学报1 51]

[25]Wang G,Wen J H,Wen X S,Yu D L,Liu Y Z 2005 Chin.J.Mech.41 107(in Chinese)[王刚,温激鸿,温熙森,郁殿龙,刘耀宗2005机械工程学报41 107]

[26]Li L,Liu Y Z,Yu D L 2006 J.Vib.Shock 25 632(in Chinese)[李黎,刘耀宗,郁殿龙2006振动与冲击25 632]

[27]Wen Q H,Zuo S G,Wei H 2012 Acta Phys.Sin.61 034301(in Chinese)[文岐华,左曙光,魏欢2012物理学报61 034301]

[28]Zhang Y F 2014 M.S.Dissertation(Changsha：National University of Defense Technology)(in Chinese) [张亚峰2014硕士学位论文(长沙：国防科学技术大学)]

[29]Zhang H,Wen J H,Xiao Y,Wang G,Wen X S 2015 J. Sound Vib.343 104

[30]Zhang H,Xiao Y,Wen J H,Yu D L,Wen X S 2016 Appl. Phys.Lett.108 1734

[31]Mei J,Ma G,Yang M,Yang Z,Wen W,Sheng P 2012 Nat.Commun.3 132

PACS:07.10.Fq,46.40.—f,62.30.+d,68.43.Pq DOI:10.7498/aps.66.140701

Flexural vibration band gaps for a phononic crystal beam with X-shaped local resonance metadamping structure∗

Du Chun-Yang Yu Dian-Long†Liu Jiang-WeiWen Ji-Hong
(Laboratory of Science and Technology on Integrated Logistics Support,National University of Defense Technology,
Changsha 410073,China)

7 March 2017;revised manuscript

19 April 2017)

Structural vibration is commonly seen in engineering,which can cause resonance and fatigue damage in structure. Therefore,it is very desirable in vibration control techniques to achieve structure with low-frequency and broadband damping feature.In this paper,we design a phononic crystal(PC)beam with X-shaped locally resonant metadamping (XLRMD)structures.Based on the PC theory,the fl exural wave propagation in XLRMD beam is studied.The equivalent dynamic properties of the XLRMD structure are analyzed by Lagrange equation.It is shown that due to its geometric nonlinearity,the XLRMD can e ff ectively increase the damping of the system,which is validated by the transfer matrix method.The in fl uence of structural parameters of XLRMD on band gap characteristics of the PC beam is then discussed in detail by using the fi nite element method with COMSOL multiphysics software in conjunction with Matlab, where the PC beam with XLRMD is modeled with the multi-body dynamic module within COMSOL and the band gap characteristics are calculated.The damping properties of the system are studied also using the fi nite element method. It is shown that compared with the equivalent structures,the PC beam with XLRMD can magnify the damping of the structure system,demonstrating a meta-damping phenomenon.The XLRMD in the PC beam can not only generate lower frequency and wider range band gaps but also suppress the vibration in passband ranges.This can bring a new design for reducing the vibration of structural systems.

phononic crystals,band gap,metadamping,geometric nonlinearity

:07.10.Fq,46.40.—f,62.30.+d,68.43.Pq

10.7498/aps.66.140701

∗国家自然科学基金(批准号：11372346)资助的课题.

†通信作者.E-mail：dianlongyu@vip.sina.com

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant No.11372346).

†Corresponding author.E-mail：dianlongyu@vip.sina.com