血压测量的EEMD和ANN的方法研究
2017-08-08吴育东钟舜聪沈耀春
【作 者】吴育东,钟舜聪,,沈耀春,
1 福州大学机械工程及自动化学院光学/太赫兹及无损检测实验室,福州市,350108 2 福建省医疗器械和生物技术重点研究室,福州市,350108 3 英国利物浦大学电气电子工程系,利物浦,L693BX,英国
血压测量的EEMD和ANN的方法研究
【作 者】吴育东1,钟舜聪1,2,沈耀春1,3
1 福州大学机械工程及自动化学院光学/太赫兹及无损检测实验室,福州市,350108 2 福建省医疗器械和生物技术重点研究室,福州市,350108 3 英国利物浦大学电气电子工程系,利物浦,L693BX,英国
血压是衡量人体心血管系统功能的一个重要指标。该文针对电子血压计不能实现血压的无创连续测量等问题,提出一种基于EEMD和ANN算法的无创血压测量方法。实验分析了MIMIC数据库中的19 500个脉搏波信号,通过EEMD对脉搏波进行分解,提取第4层分解信号的10个特征参数作为ANN的输入,脉搏波对应的血压作为ANN的输出进行血压模型的训练,并对模型进行误差分析。实验结果表明,模型的测试误差达到美国医疗器械促进协会(AAMI)制定的标准,通过该方法可实现血压的无创连续测量。
血压;光电容积脉搏波;集合经验模态分解;神经网络
0 引言
血压表征血液对血管壁的侧压力,通过对人体血压的连续监测,可以很好地反映出人体心血管系统功能的好坏。现实生活中通常用电子血压计进行血压测量[1],该方式的主要缺点是只能间断性获得人体血压,并且测量过程中充气袖套的使用会给测量者带来不适感。
先前许多学者寻求通过脉搏波传输时间(Pulse Transit Time,PTT)估计人体血压[2-3]。其原理是同时获取人体的ECG[4]和PPG[5-7]信号,利用这两路信号实现PPT的计算,最后通过PTT与血压建立的模型间接计算血压。这种方法需要采集两路信号,增加了设备系统的复杂性,限制了仪器的小型化,不利于便携式携带实现24 h的连续监测。
后来有些学者提出基于单个PPG信号对血压的测量方法[8-9]。李章俊等[10]学者也做了关于PPG时域波形与血压相关性的研究。根据脉搏波的机理,分析PPG信号的时域波形特征参数与血压的相关性,这些探索给出了使用脉搏波特征参数法计算血压的理论基础。
然而临床中通过对大量的脉搏波数据分析表明,人体脉搏波的波形特征会随着人体的生理因素的变化而变化[11]。图1为4个不同类型的PPG信号,可以看出不同人的PPG信号有所差异,特别是信号中重搏波部分越来越不明显,PPG波形特征的变化会影响特征参数的提取导致血压计算精度下降。
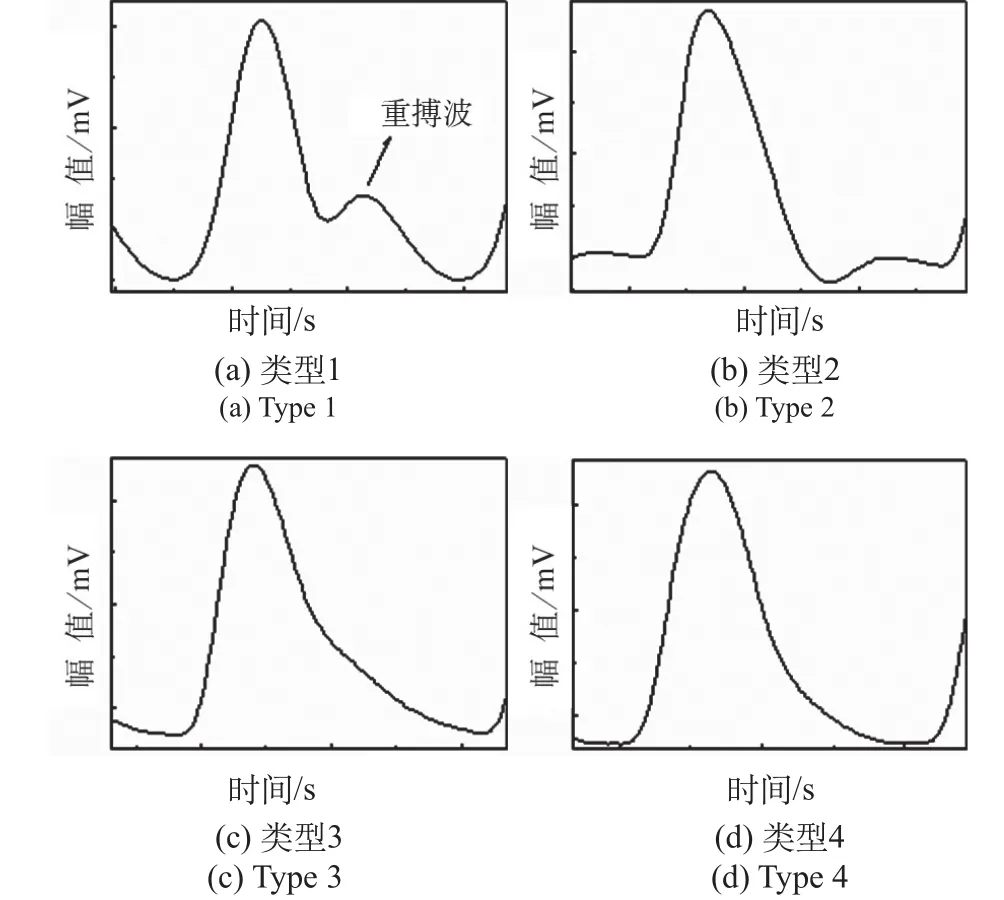
图1 不同类型的PPG信号Fig.1 Different types of PPG signals
针对上述问题,本文提出一种基于EEMD和ANN的新的无创血压计算方式。通过EEMD对原始PPG信号进行分解,提取第4层分解信号的10个特征参数作为ANN的矢量输入,以及每个PPG对应的SBP(Systolic Blood Pressure)和DBP(Diastolic Blood Pressure)作为ANN的矢量输出进行训练拟合,通过该方法间接实现血压的无创连续检测。
2 实验原理
2.1 EEMD集合经验模态分解原理
集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)是剖析非平稳信号的新方式,可以避免模态混叠效应。
EEMD的分解过程如下所示:
第一步:对待分析的信号序列x(t)实行插入M次(M>1)高斯白噪声ni(t)(i=1, ..., M)处理[12]:

第二步:通过EEMD算法对添加过白噪声的信号序列xi(t)实行分析,得出各层的IMF分量,标记为cij(t)[13]。
第三步:由于在进行EEMD计算时,多次添加了高斯白噪声,将对分解得到的IMF产生影响,所以对IMF分量cij(t) 实行整体平均处理。

式中,cj(t) 为最后通过EEMD解析获得的真实的IMF,M代表所添加白噪声的数量。
本研究对脉搏波信号进行添加200次白噪声的EEMD分解,并对分解得到的各层IMF进行分析。图2与图1相对应:表示不同特征的脉搏波和对应的第4层IMF分量。通过对不同特征的PPG信号进行EEMD分解分析,发现无论原始信号重播波是否明显,在第4层IMF都能体现出来。原始信号的有用高频成分大部分都分布在第4层分量中(以下简称c4层),且c4层每搏信号在时间尺度上与每搏PPG信号一一对应,所以本文以c4层作为研究对象,提取c4层的特征参数做为ANN的拟合输入。

图2 不同类型的PPG信号和对应的第4层IMF分量Fig.2 Different characteristics of the PPG signals and the corresponding component of the layer 4 of the IMF.
图3 为c4层的10个特征参数,PPG信号先通过EEMD分解获得c4层分量。再利用差分阈值法计算c4层每搏波形信号的主动脉瓣开放点A1,收缩期最高压力点B1,降中峡点C1,重搏波点D1等特征点[14-15],在此基础上提取10个特征参数:主波B1点的幅值Hb,降中峡点C1点的幅值Hc,重搏波点D1的幅值Hd。时间参数有主波点B1点到起始点A1的时间Tb,降中峡点C1点到起始点A1的时间Tc,重播波点D1点到起始点A1的时间Td,以及每个单波的总时间T。面积参数有起始点A1到主波点B1的面积s1,主波点B1到下一个波起始点面积s2,以及总面积s。以这10个特征参数作为ANN的输入。
2.2 BP神经网络原理
20世纪80年代中期,Rumelhart和McCelland提出了误差反向传播算法,即BP(Back Propagation)神经网络算法[16]。算法在实行网络的训练时,数据的传输是从输入层到输出层正向传输,而在训练各层权值时,则是按照误差降低的方向,从输出层通过隐含层逆向地逐层订正,训练的过程中重复正向数据传播和反向权值订正,直到网络的输出与期望输出的误差达到设定的数值,或是到达设定的训练次数,网络停止训练。
本研究设计了单隐层的网络结构形式,如图4所示:当中隐含层使用sigmoid函数,输出层则是线性的,训练时采取Levenberg-Marquardt算法[17],即trainlm函数。以c4层提取的10个特征参数作为输入层的输入矢量。隐含层共包含30个神经元,以每搏PPG信号对应的SBP和DBP作为输出层。

图3 c4层信号的10个特征参数Fig.3 Extraction of c4 layer signal characteristic parameters of 10

图4 BP神经网络结构图Fig.4 The BP neural network structure
2.3 MIMIC 数据库
实验中分析的指尖PPG信号和对应的SBP和DBP数据都来自于THE MIMIC DATABASE[18-20],该数据库记录了多种生理信号和生命体征。这些信号中大多数包括了心电图、血压、PPG信号,以125 Hz采样频率记录保存。图5为PPG信号和对应的BP信号,本研究以PPG信号进行分析,提取特征参数作为ANN的输入,数据库记载的每搏ABP信号的收缩压和舒张压作为ANN的输出,实行训练。
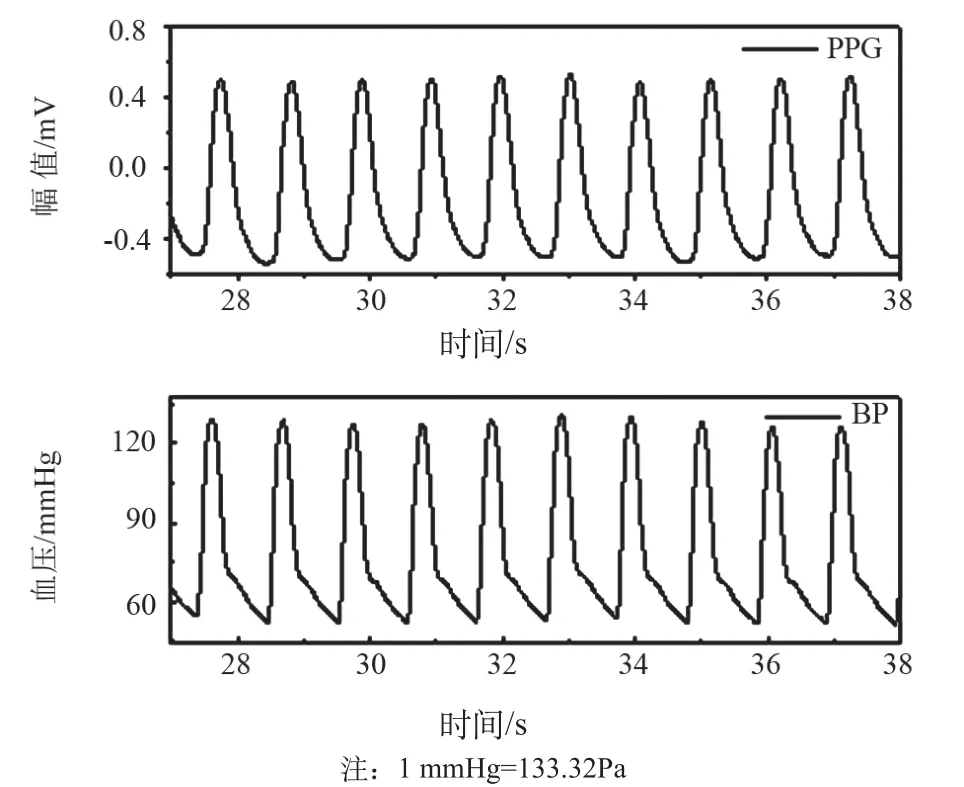
图5 数据库中的PPG信号和对应BP信号Fig.5 PPG signal and BP signal in database
3 实验结果与分析
本研究总共计算了不同人的19 500个每搏PPG信号和信号对应的SBP和DBP。把这些数据分为ANN模型训练和测试两部分,其中18 000个作为模型训练数据,1 500个作为模型测试数据。
3.1 模型训练
利用18 000个数据参与ANN模型训练,并且设置训练样本占整个训练数据的70%,验证样本和测试样本各占15%。根据训练数据的误差直方图和R值来判定所训练模型的性能。
图6表示血压模型评估,图6(a)表示整个训练数据的误差直方图。误差计算公式为:误差=目标输出(T)—实际输出(Y)。如图可以看出误差大部分集中在0附近。图6(b)为训练数据的回归图,如图所示训练样本、验证样本、测试样本及全部数据的R值依次为:0.982 56,0.980 92,0.981 99,0.982 23。根据误差直方图和回归图可以看出训练模型良好。
3.2 模型测试
取1 500个每搏PPG信号作为模型的测试估计。图7为测试数据SBP和DBP的误差直方图,其中误差e由下面公式计算得到:

式中BPest为经过ANN训练模型估计出的SBP或者DBP,而BP为对应数据库中的实际值。
表1为测试结果统计,其中绝对误差ea由下面公式计算得到:

表1中以SBP和DBP对应的绝对误差ea的均值和标准差作为误差结果分析(均值±标准差)。
由表1可知,通过该方法估算的血压与实际值的误差满足美国医疗器械促进协会(AAMI)颁发的评价血压计精确性的国际标准[21],即,设备实测的血压与标准血压计之间的绝对误差ea的均值必需小于5 mmHg,标准差必须小于8 mmHg。

图6 训练模型性能评估图Fig.6 Performance evaluation of training model

表1 实验及结果Tab.1 Experiment and results
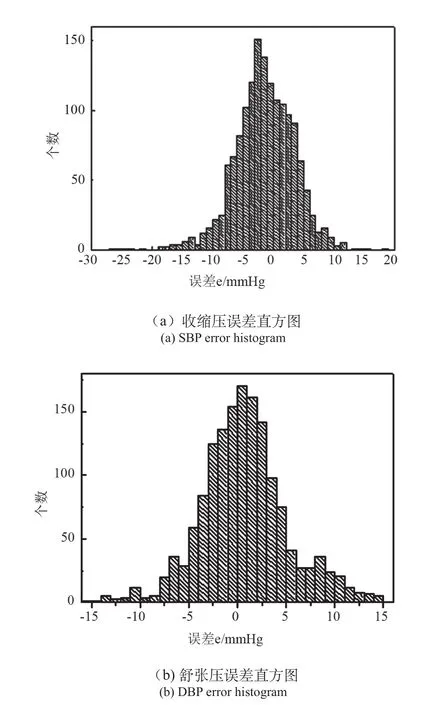
图7 血压误差直方图Fig.7 Blood pressure error histogram
4 实验总结
许多学者研究通过PPG信号实行无创血压的检测。然而大部分只研究原始PPG信号特征参数与血压的关系,提出了各个特征参数与血压的线性关系,Kurylyak Y[22]等学者就根据舒张时间与血压的线性模型去估计血压,得出的结论是收缩压绝对误差ea的均值为9.80 mmHg,标准差为8.94 mmHg,舒张压绝对误差ea的均值为5.88 mmHg,标准差为5.11 mmHg,表明通过特征参数与血压的线性关系去估算血压误差较大。然而人体的脉搏波信号会随着生理因素的变化而出现一系列变化,导致有些脉搏波的特征点没有显现出来,影响了特征参数的提取。因此本文提出了通过PPG信号无创测量血压的新方式。利用EEMD算法对原始PPG信号实行分解,以分解信号的第4层为研究对象。提取第4层分解信号的10个特征参数进行ANN的矢量输入,以每搏PPG信号对应的SBP和DBP作为ANN的矢量输出。总共分析了数据库中19 500个PPG信号,根据测试的结论SBP绝对误差ea为(3.96±3.30)mmHg ,DBP绝对误差ea为(3.38±3.30)mmHg,达到了美国医疗器械促进协会(AAMI)颁发的评价血压计准确性的国际标准,即绝对误差ea应在 (5.00±8.00)mmHg以内。该方法为智能穿戴等设备实现血压的无创连续测量提供一定的参考价值。
[1] 段于千, 胡平平. 无创血压测量示波法分析与研究[J]. 微计算机信息, 2011, 27(1): 102-103.
[2] Xu L, Gao K. Continuous cuffless arterial blood pressure measurement based on PPG quality assessment[J]. Int J Comput Biol Drug Design, 2015, 8(2): 150-158.
[3] 白丽红, 王成, 文苗, 等. 基于脉搏波传导时间的连续血压监测系统[J]. 生物医学工程研究, 2014, 33(4): 221-225.
[4] Lin H D, Lee Y S, Chuang B N. Using dual-antenna nanosecond pulse near-field sensing technology for non-contact and continuous blood pressure measurement[C]//2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE, 2012: 219-222.
[5] 邹滋润, 陈真诚, 朱健铭. 基于光电容积脉搏波的呼吸波提[J]. 中国生物医学工程学报, 2013, 32(4): 508-512.
[6] 张天淼, 朱兰. 光体积描记术原理及应用[J]. 中国医疗器械杂志, 2016, 40 (3): 186-190.
[7] 王步青, 柴晓珂, 张政波, 等. 心电图和光电容积脉搏波计算心率变异性的比较研究[J]. 中国医疗器械杂志, 2015, 39(4): 249-252.
[8] Yoon Y Z, Yoon G W. Nonconstrained blood pressure measurement by photoplethysmography[J]. J Opt Soc of Korea, 2006, 10(2): 91-95.
[9] Fortino G, Giampa V. PPG-based methods for non invasive and continuous blood pressure measurement: an overview and development issues in body sensor networks[C]//Medical Measurements and Applications Proceedings (MeMeA), 2010 IEEE International Workshop on. IEEE, 2010: 10-13.
[10] 李章俊, 王成, 朱浩, 等. 基于光电容积脉搏波描记法的无创连续血压测量[J]. 中国生物医学工程学报, 2012, 31(4): 607-614.
[11] 罗志昌, 张松, 杨益民. 脉搏波的工程分析与临床应用[M]. 北京:科学出版社, 2006.
[12] 陈仁祥, 汤宝平, 马婧华. 基于 EEMD 的振动信号自适应降噪方法[J]. 振动与冲击, 2012, 31(15): 82-86.
[13]张碧薇. 基于 EEMD 与平稳小波变换的脉搏波形特征分析研究[D]. 北京:北京工业大学, 2013.
[14] 季忠, 刘旭. 基于波形特征和小波的脉搏波特征点识别研究[J].仪器仪表学报, 2016, 37(2): 379-386.
[15] 徐可欣, 王继寸, 余辉, 等. 脉搏波时域特征与血压相关性的研究[J]. 中国医疗设备, 2009 (8): 42-45.
[16] 周品. MATLAB 神经网络设计与应用[M]. 北京:清华大学出版社, 2013.
[17] 王丽萍. 基于 BP 神经网络工具箱实现函数逼近[J]. 湖南农机(学术版), 2011 (5): 29-31.
[18] Madhav K V, Ram M R, Krishna E H, et al. Robust extraction of respiratory activity from ppg signals using modified mspca[J]. IEEE Trans Instrument Measur, 2013, 62(5): 1094-1106.
[19] Sayadi O, Shamsollahi M B. Utility of a nonlinear joint dynamical framework to model a pair of coupled cardiovascular signals[J]. IEEE J Biomed Health Inform, 2013, 17(4): 881-890.
[20] Li P, Liu M, Zhang X, et al. Novel wavelet neural network algorithm for continuous and noninvasive dynamic estimation of blood pressure from photoplethysmography[J]. Sci Chin Inform Sci, 2016: 59(4):1-10.
[21] Heusdens J F, Lof S, Pennekamp C W A, et al. Validation of non-invasive arterial pressure monitoring during carotid endarterectomy[J]. Brit J Anaesthesia, 2016, 117(3): 316-323.
[22] Kurylyak Y, Lamonaca F, Grimaldi D. A neural networkbased method for continuous blood pressure estimation from a PPG signal[C]//2013 IEEE International Instrumentation and Measurement Technology Conference (I2MTC). IEEE, 2013: 280-283.
Noninvasive Continuous Blood Pressure Measurement Method Based on EEMD and ANN
【 Writers 】WU Yudong1, ZHONG Shuncong1,2, SHEN Yaochun1,3
1 Laboratory of Optics, Terahertz and Non-destructive Testing & Evaluation, School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, 350108 2 Fujian Key Laboratory of Medical Instrument and Pharmaceutical Technology, Fuzhou, 350108 3 Department of Electrical Engineering and Electronics, University of Liverpool, Liverpool, L693BX, UK
blood pressure, photoplethysmography signal, ensemble empirical mode decomposition, artificial neural networks
R318.6
A
10.3969/j.issn.1671-7104.2017.04.001
1671-7104(2017)04-0235-05
2016-12-12
国家自然科学基金资助项目(51675103);教育部高等学校博士学科点科研基金(博导类:20133514110008);国家卫生和计划生育委员会科研基金(WKJ-FJ-27);福建省杰出青年基金(滚动资助计划,2014J07007)
钟舜聪,E-mail:zhongshuncong@hotmail.com
【 Abstract 】Blood pressure is an important index to measure the function of human cardiovascular system. In order to solve the problem of non-invasive continuous measurement of blood pressure in electronic sphygmomanometer, a noninvasive blood pressure measurement method based on EEMD (ensemble empirical mode decomposition) and ANN (artificial neural networks) were proposed. In the experiment, a total of 19 500 pulse wave signals from THE MIMIC DATABASE were analyzed and subsequently the pulse wave was decomposed by EEMD. Furthermore, 10 characteristic parameters of the 4th layer decomposition signal were extracted as the input of ANN. The blood pressure corresponding to the pulse wave was taken as the output of ANN to train the BP (blood pressure) model. The error analysis of the model was carried out. The results indicated that the error of the model meets the standards of the American Association for the advancement of medical instrumentation (AAMI). Therefore, this method can be employed in noninvasive continuous measurement of blood pressure.
