三轴磁传感器快速标定方法研究

王庆宾 张晓明

（1.中北大学 电子测试技术国家重点实验室，山西 太原 030051；2.中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051）

三轴磁传感器快速标定方法研究

王庆宾1， 张晓明1，2

（1.中北大学 电子测试技术国家重点实验室，山西 太原 030051；2.中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051）

针对现有的三轴磁传感器标定过程比较复杂，而且对环境要求较高等问题。提出基于椭球拟合的三轴磁传感器标定方法，利用绕“8”字的方式实现三轴磁传感器快速标定。采用基于最小二乘的椭球拟合方法标定三轴磁传感器的零点误差、灵敏度误差、不正交角误差。建立绕“8”字方式标定准确度的评价指标角度覆盖度，通过实验研究得到角度覆盖度必须达到1.3以上才能得到高准确度的标定参数。通过标定朝向与角度覆盖度综合实验，得到提升标定准确度的绕“8”字操作方法，简化标定过程。

三轴磁传感器；标定补偿；椭球拟合；绕“8”字

0 引 言

目前获取高准确度的地磁场数据信息是完成精准导航的前提条件，有必要采用合理的方法完成三轴磁传感器的标定以获取较为准确的地磁场数据。现有的磁传感器标定方法有：十二位置法与加速度信息相结合的方法[1-2]，其优点是操作起来会比较方便；采用迭代算法对三轴磁传感器标定补偿[3-4]，可用于在线标定，但该方法标定的准确度较低；使用共轭梯度法[5]标定磁传感器，其优点是标定的准确度高；利用外加磁场法进行标定[6-7]，可以得到比较合适的误差参数，但所需外界条件的要求比较高；椭圆假设法[8-9]要求载体在一个平面内运动，对于载体的运动姿态具有一定的限制。以上方法都有各自的优点，但是其标定过程对外界环境的要求相对较高，不易于现场标定的实现[10]。

本文提出基于最小二乘椭球拟合法的绕“8”字三轴磁传感器快速标定方法。相比于以上方法，不需要载体的姿态基准并且易于完成[6-10]，具有所需数据量小、算法简单、得到的标定参数准确度较高等优点[11]。

1 最小二乘椭球拟合方法

1.1 误差模型的建立

一般地影响三轴磁传感器标定的主要误差来源为零点误差、灵敏度误差和不正交角误差[12]。综合考虑单轴和三轴磁传感器轴间误差[13]，可以得到三轴磁传感器误差模型如下所示：

式中：Hm——实际三轴磁传感器的测量值；

Hme——理想三轴磁传感器的测量值；

H0——磁传感器的零点误差值；

K1——角度误差矩阵；

α、β、γ——实际三轴磁传感器测量轴与理想坐标系中三轴的角度误差；

K2——灵敏度误差矩阵；

kx、ky、kz——x、y、z轴的灵敏度。

设理想三轴磁传感器的测量轴为x、y、z，而实际磁传感器的测量轴为x1，y1，z1，三者近似两两正交；设z与z1轴重合，x1位于xoz平面内与x轴夹角为α；y1轴在xoy平面内的投影与y轴的夹角为β；与xoy平面的夹角为γ，如图1所示。理想三轴磁传感器中不正交角α、β、γ均为0。三轴磁传感器轴间不正交的误差模型为

图1 不正交角示意图

其中K-1=K1-1K2-1。

1.2 最小二乘法求标定参数

最小二乘法原理是利用求残余误差平方和为最小的一种数据处理方法。基于最小二乘的椭球拟合算法的本质就是得到一个椭球曲面方程使得测量数据与该椭球曲面之间距离的平方和为最小[14]。

由于椭球面为一个二次曲面，则设该二次曲面方程：

式中：ξ——待求的二次曲面参数向量，ξ=[a，b，c，d，e，f，p，q，r，g]T；

z——测量数据的运算组合向量，z=[x2，y2，z2，2xy，2xz，2yz，2x，2y，2z，1]T；

F（ξ，z）——测量数据（x，y，z）到二次曲面

F（ξ，z）=0的代数距离[15]。

在基于最小二乘的思想下，利用该方法来完成三轴磁传感器输出数据拟合椭球曲面最基本的原理就是使输出数据点集与拟合后椭球曲面的距离平方和为最小，于是可以得到拟合后椭球曲面方程为

等式（4）中，A代表椭球二次曲面的形状参数矩阵：

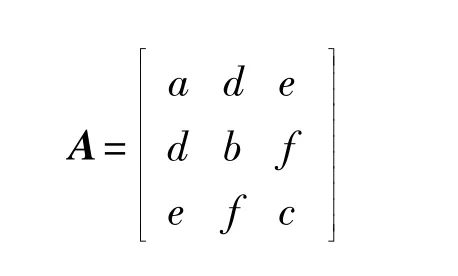
X表示采集数据点集；X0表示所得曲面的中心坐标向量：

将式（4）展开可以得到如下等式：

传统椭球拟合所需数据分布在整个椭球面上，如图2所示。在整个数据采集过程中需要大量采样点，操作较为复杂[16]，相比绕“8”字法（见图 3）要复杂很多。绕“8”字法只需要采集一个或几个“8”字数据。

图2 椭球拟合图

图3 绕“8”字图

2 绕“8”字标定方法

绕“8”字标定方法是针对现场快速标定的一种方法，其操作简单，需要的辅助设备少。影响标定质量的两个主要因素是标定朝向、角度覆盖度。朝向因素是由于地磁场在各个方向的分布不一样，在不同朝向绕“8”时得到的椭球形状也不一样，标定质量受到影响；角度覆盖度主要反映采样点在椭球面上的分布情况。

2.1 朝向的定义及“8”字绕法

图4 中，o-xyz为东北天地理坐标系；o-x′y′z′为传感器坐标系；ox″为ox′在o-xy平面上的投影，θ为ox′与o-xy平面的夹角，φ为ox″与ox的夹角。θ和φ在地理坐标下表现为俯仰角和偏航角即三轴磁传感器的朝向角，下文中用（φ，θ）表示朝向。“8”字形为三轴磁传感器的绕法，箭头指向方向为绕“8”字的走向即在平面内画“8”字。

图4 绕“8”字形状及朝向定义

2.2 采样点角度覆盖度分析

绕“8”字法标定只需较少的数据点就能得到标定参数，但是其采样点的分布对标定准确度有较大影响。为对采样点的分布情况做更好的评判，提出角度覆盖度来评判标定的好坏。角度覆盖度模型如图5所示。P为某一个采样点，P′为P在xoy平面内的投影点，并且Θ是oP线与平面xoy之间的夹角，Ψ为oP′与x轴之间的夹角，于是通过这两个角度的大小便可以描述“8”字形状角度覆盖度的大小，并且可以确定出Θ的最大角度为180°，Ψ的最大角度为360°。

Θ的求解公式为

其中x、y、z分别为磁测系统输出数据点集的坐标。

以x轴的正向为基准求解Ψ：

通过式（6）与式（7）可以计算出其数据分布的范围，得到Θ和Ψ的最大值和最小值。则其角度覆盖度c的计算公式为

由式（8）可以得到c为0～2的数值。角度覆盖度越大表明数据点集在拟合后椭球曲面所占的范围越大，因此所拟合出的椭球效果越好；而当角度覆盖度较小时，拟合误差较大，拟合效果差。

图5 角度覆盖度评价指标模型图

3 实验结果

3.1 标定朝向因素分析

研究绕“8”字标定朝向的影响因素时，在实验的过程中选择了6个朝向进行研究，分别为（0，0）、（90°，0）、（180°，0）、（270°，0）、（0，90°）、（0，-90°）。在6个朝向分别绕“8”，为避免出现偶然误差每组重复做3次，其结果如表1所示。

由表中数据可以看出在朝向为（90°，0）磁场误差比传统标定方式的准确度高，其他朝向上的磁场误差较大，即在朝向为（90°，0）标定质量最高。

3.2 角度覆盖度因素分析

角度覆盖度直接影响着标定质量，对其影响情况做了相应的实验，实验结果如表2所示。

表1 朝向对标定质量影响的实验结果

表2 角度覆盖度对标定质量影响的实验结果

表3 单个朝向所得的实验结果

表4 任意两个朝向组合所得的实验结果

由表可知，随着角度覆盖度的增大，磁场误差减小，当角度覆盖度达到1.3时标定的质量保持稳定，即标定时尽量保证角度覆盖度在1.3以上。为了探究标定朝向与角度覆盖度之间的关系，做了以下研究。

3.3 朝向因素与角度覆盖度因素综合分析

在单个朝向的情况下其角度覆盖度的结果如表3所示。在单个朝向的情况下角度覆盖度都不能达到1.3以上，其标定的质量也相对较低。

对两个任意朝向进行组合，每个组合进行3次实验，其结果如表4所示。任意两个朝向组合后磁场误差明显变小，相比于传统标定方法，其磁场误差更小，而且角度覆盖度基本接近于2。

表5 3种标定方法结果比较

分别用3种方法对三轴磁传感器进行多次标定，其误差平均值如表5所示。可以看出，绕“8”字法得到的磁场误差值要小于其他方法，综上使用绕“8”字标定方法时要采用两个朝向画“8”字，才能得到较高准确度的标定参数。

4 结束语

对于三轴磁传感器的快速标定，本文提出的绕“8”字法具有所需数据量小、标定过程简单，得到的标定参数准确度较高等优点，适合于三轴磁传感器现场快速标定。并得出以下结论：1）角度覆盖度必须达到1.3以上才能得到高准确度的标定参数。2）使用绕“8”字标定方法时，采用两个朝向画“8”字能保证角度覆盖度都在1.9以上，并得到较高准确度的标定参数，达到指标要求。

[1]张娇，陈静，杨栓虎.三轴磁阻式传感器标定方法的研究[J].弹箭与制导学报，2010，30（6）：46-48.

[2]陈文荣，张婧.三轴磁传感器制造误差补偿方法研究[J].现代防御技术，2015，43（6）：190-193.

[3]盛蔚，蒋勇.三轴磁传感器系统的在线标定[J].弹箭与制导学报，2015，35（3）：179-182.

[4]王萌夏，吴益飞，于斌.基于迭代算法的三轴磁传感器标定与误差补偿技术研究[J].兵工自动化，2015，34（2）：81-85.

[5]SABER T，RAJESH R.Magnetic sensor-based large distance position estimation with disturbance compensation[J].IEEE Sensors Journal，2015，15（8）：4249-4257.

[6]范玉宝，李杰，张晓明，等.基于椭球拟合的微惯性测量组合现场快速标定方法[J].传感技术学报，2011，24（11）：1547-1550.

[7]朱建良，王兴全，吴盘龙，等.基于椭球曲面拟合的三维磁罗盘误差补偿算法[J].中国惯性技术学报，2012，20（5）：562-566.

[8]FANG J C H， SUN H W， CAO J J， et al.A novel calibration method of magnetic compass based on ellipsoid fitting[J].IEEE Transactions on Instrumentation and Measurement，2011，60（6）：2053-2061.

[9]ZHANG X M，GAO L Z.A novel auto-calibration method of the vector magnetometer[C]∥IEEE International Conference on Electronic Measurement&Instrument，2009.

[10]MARKOVSKY I， KUKUSH A， HUFFEL S V.Consistent leastsquares fitting of ellipsoids[J].Numerische Mathematik，2004，98（1）：77-194.

[11]FITZGIBBON A，PILU M，FISHER R.Direct leastsquare fitting of ellipses[C]∥Process International Conference on Pattern Recognition，1996：253-257.

[12]杨晓东，王炜.地磁导航原理[M].北京：国防工业出版社，2009：67-80.

[13]VOJTĚCH P， VIKTOR F， ANTOIN P.Cross-field effect in a triaxial AMR magnetometer with vector and individual compensation of a measured magnetic field[J].IEEE Transactions on Magnetics，2016（76）：1-5.

[14]PANG H F， PAN M C， CHEN J F， et al.Integrated calibration and magneticdisturbance compensation of three-axis magnetometers[J].Measurement，2016（93）：409-413.

[15]FITZGIBBON A，PILU M，FISHER R B.Direct least square fitting of ellipses[J].IEEE Transactions on Pattern Analysisand MachineIntelligence，1999，21（5）：476-480.

[16]ZHANG Q， PANG H F， WAN C B.Magnetic interference compensation method for geomagnetic field vector measurement[J].Measurement，2016（91）：628-633.

（编辑：李妮）

Research of fast calibration method of three-axis magnetic sensor

WANG Qingbin1， ZHANG Xiaoming1，2
（1.National Key Laboratory for Electronic Measurement Technology，North University of China，Taiyuan 030051，China；2.Key Laboratory of Instrumentation Science&Dynamic Measurement of Ministry of Education，North University of China，Taiyuan 030051，China）

Aiming at the complicated calibration process of existing three-axis magnetic sensor and higher requirements for environment，a calibration method of three-axis magnetic sensor based on ellipsoid fitting that used an 8-shaped figure to achieve rapid calibration of three-axis magnetic sensoris was proposed.A calibration experiment was conducted in an 8-shaped figure and three errors， offset and sensitivity and nonorthogonality， were calibrated by using ellipsoid fitting method based on least squares.The angular coverage of the evaluation index around an 8-shaped calibration precision was established.The experimental results show that the angle coverage must reach 1.3 or above to obtain high accuracy calibration parameters.Through the comprehensive experiment of calibration orientation and angle coverage， the operation method of raising the calibration precision around an 8-shaped is obtained，and the calibration process is simplified.

three-axis magnetic sensor； calibration and compensation； ellipsoid fitting； an 8-shaped figure

A

：1674-5124（2017）07-0035-05

10.11857/j.issn.1674-5124.2017.07.007

2016-10-19；

：2016-12-05

王庆宾（1990-），男，山东聊城市人，硕士研究生，专业方向为地磁导航。