镍基高温合金疲劳-蠕变寿命预测的临界面损伤方法
2017-08-08董成利于慧臣
董成利, 于慧臣
(1 北京航空材料研究院 航空材料检测与评价北京市重点实验室,北京 100095; 2 北京航空材料研究院 材料检测与评价航空科技重点实验室,北京 100095; 3 北京航空材料研究院 先进高温结构材料重点实验室,北京 100095)
镍基高温合金疲劳-蠕变寿命预测的临界面损伤方法
董成利1,2,3, 于慧臣1,2,3
(1 北京航空材料研究院 航空材料检测与评价北京市重点实验室,北京 100095; 2 北京航空材料研究院 材料检测与评价航空科技重点实验室,北京 100095; 3 北京航空材料研究院 先进高温结构材料重点实验室,北京 100095)
采用临界面损伤方法并耦合疲劳-蠕变寿命模型,通过适当的技术改进,分别对某型航空发动机650 ℃条件下涡轮盘用材料ZSGH4169高温合金和980 ℃条件下涡轮转子叶片用材料DZ125定向凝固高温合金的疲劳-蠕变寿命进行预测,并分别比较以Walls,Ccb,Swt,Glk,和Fin为参数的五种寿命模型的预测精度。算例的计算结果表明:对于ZSGH4169高温合金,以Walls临界损伤平面为参数的寿命模型预测效果较好,预测的结果与实验值相比基本落在±3倍分散带以内;而对于DZ125高温合金而言,以Glk临界损伤平面为参数的寿命模型预测效果较好,预测的结果与实验值相比基本落在±2.5倍分散带以内。
临界面损伤;疲劳-蠕变;寿命预测;定向凝固;相关系数
对机械零部件失效的统计表明,75%~80%属于疲劳破坏,这是抗疲劳设计成为现代设计重要组成部分的主要原因[1]。同时,随着当代社会经济的全面发展,对航空器在设计和使用中的安全性、可靠性、经济性和环境友好性的要求日趋迫切和严格,使得航空器结构特别是热端部件的疲劳(寿命)问题受到日益广泛的关注。目前及未来相当长一段时间内,航空、舰船和地面动力装置的燃气轮机热端部件(如涡轮叶片、涡轮盘和燃烧室部件)仍然会以高温合金作为主要的制造材料,但此类结构的寿命控制规律至今仍然不明朗,主要是因为高温部件的疲劳寿命控制和损耗机制及其影响因素非常复杂且繁多,如载荷、结构与材料属性、多轴应力应变状态、使用环境等都会有重要的影响[2-4]。因此,在对这类部件进行耐久性和安全性分析及评定时,部件的多轴疲劳寿命预测计算方法就显得尤为重要。
早期的疲劳寿命理论仅仅是简单地通过应用某种等效方法,如Von Mises理论[5],把结构承受的多轴应力状态下的等效应力应变与单轴应力状态下的应力应变结合起来,按照等损伤原则建立部件的疲劳寿命预测方法。Garud在总结1979年以前的相关研究结果时发现,等效应力(应变)方法对于室温比例加载情况下的多轴疲劳问题可以得到比较好的结果,但对高温非比例加载情况就显得无能为力[6]。因此,迫切需要提出一种能够表征高温非比例加载条件下的寿命预测方法。
临界损伤平面概念的提出,使得多轴疲劳问题的研究向前推进了一大步。Findley[7]最早提出临界损伤平面(Critical Damage Plane,CDP)的概念,并认为此平面上的剪应力及法向正应力是导致疲劳裂纹萌生和扩展的主要原因。Brown和Miller[8]根据临界损伤平面的概念提出临界面上的剪应变范围及其相应的正应变范围所构成的参量来处理多轴疲劳问题,并定义了两种类型的裂纹扩展模式:即A型-沿裂纹表面扩展模式;B型-向结构内部扩展模式。Lohr和Ellison[9]提出与外表面成45°平面上的剪应变及相应法向正应变用于高应变多轴疲劳寿命预测。Kanazawa等[10]研究了拉扭组合的非比例循环加载下的低周疲劳, 认为最大剪应变幅和最大剪应变面上的正应变仍是控制非比例加载疲劳寿命最重要的2个参量。Socie[11]考虑到对于具体构件的裂纹可能沿着剪切平面也可能沿着拉伸平面,因此合理的多轴疲劳寿命模型应当可以同时考虑这两种情况,在比较分析AISI304,Inconel718,SAE1045等材料的实验结果后,分别采用Fatemi,Socie和Smith等提出的疲劳参量方法成功解决了剪切型和拉伸型的多轴疲劳寿命预测问题。
目前较为认可和广泛采用的疲劳参数模型,分别涉及了剪切型、拉伸型、能量型和混合型主导的多轴疲劳。本工作利用某型航空发动机涡轮部件典型材料的高温低循环疲劳实验结果,对所选用的5个具有代表性的基于临界损伤平面法的寿命模型进行分析和评价。
1 临界损伤平面理论
1.1基于临损伤平面方法的疲劳寿命模型
通常对疲劳裂纹萌生及扩展的观察,可发现疲劳裂纹多数情况下出现在材料的一个特定的平面上,如剪切或拉伸平面,并与材料、应力状态和工作环境等因素有关,裂纹的萌生和扩展受此平面上力学参量的控制。可以采用两种方式来定义此平面:(1)最大剪应力/应变幅或最大正应力/应变幅平面;(2)以某个物理量定义的损伤达到最大的平面。目前认为基于临界损伤平面的方法是比较合理的疲劳理论,可较好的关联多轴疲劳实验结果。
Findley[7]认为在最大剪应力幅所在平面上,其上最大应力的方向为裂纹萌生和扩展的方向,所以定义了如下的参数来表示临界损伤平面:
Fin=τa+kσmax
(1)
式中:k是待定常数;τα是剪应力幅;σmax是最大应力;Fin代表临界损伤平面。
在Findley模型的基础上,Fatemi-Socie(FS)[12]引入屈服强度σy来定义临界损伤平面:
(2)
式中:k是待定常数;σn,max是法向为n的平面上的最大应力;σy是屈服应力;Δγmax是最大剪应变范围;Fs代表临界损伤平面。需要说明的是,对于各向同性材料,σy是不随材料坐标改变的,而对于各向异性材料,如定向凝固合金和单晶合金,在不同晶体方向上,σy是变化的,这造成了FS模型实际应用的困难。
Walls应用八面体面上最大剪应变γmax和最大正应变εmax的组合来定义临界损伤平面[13]:

(3)
式中:γmax是八面体面上最大剪应变;εmax是八面体面上最大剪应变;Walls代表临界损伤平面。
Smith-Watson-Topper(SWT)认为,临界面由最大正应变Δεmax来确定,而临界滑移方向是最大正应力所在的方向[9]:
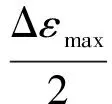
(4)
式中:Δεmax是最大正应变范围;Swt代表临界损伤平面。
Glinka[14]综合考虑了剪应变幅Δγ/2和剪应力幅Δτ/2的乘积、正应变幅Δεn/2和正应力幅Δσn/2的乘积,用二者的算术和确定临界损伤平面:
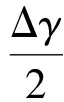
(5)
式中:Δγ/2和Δεn/2是剪应变幅和正应变幅;Δτ/2和Δσn/2是剪应力幅和正应力幅;Glk代表临界损伤平面。
Chu-Conle-Bonnen(CCB)认为,也可采用最大剪应力τn,max和剪应变幅Δγ/2的乘积与最大正应力σn,max和正应变幅Δε/2的乘积之和来确定临界损伤平面[15-16]:
(6)
式中:Δγ/2和Δε/2是剪应变幅和正应变幅;τn,max和σn,max是最大剪应力和最大正应力;Ccb代表临界损伤平面。
1.2临界损伤平面法预测疲劳寿命的步骤
临界损伤平面法预测疲劳寿命的一般步骤分为以下10步。
(1)进行结构有限元分析,可以是弹性的,也可以是弹塑性的,如果有先进黏塑性统一本构模型,最好能进行结构的黏塑性应力应变分析,求得给定载荷工况下结构的应力应变场和损伤场,找出最大等效应力或最大损伤所对应的节点和单元,并获得该节点处的应力和应变历史数值。
(2)考虑一个待选定平面(有k个),其上有单位法矢n,n在坐标轴系XYZ内,定义n的特征角度如下:n与Z轴的夹角为θ;n在XY平面内的投影与X轴的夹角为θR,初始时,令θ=θR,如图1所示。

图1 临界损伤平面定义示意图Fig.1 Schematic diagram of critical damage plane
(3)计算n的方向余弦数(即待选平面的方向余弦数):
nx=sinθsinθR;ny=-sinθcosθR;nz=cosθ
(7)
(4)在每个时间点上,计算正应变ε、正应力σ和剪应变γ、剪应力τ:
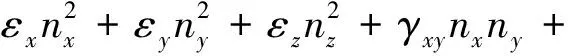
(8a)
σ=XNnx+YNny+ZNnz
(8b)
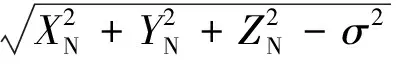
(8c)

(8d)
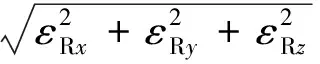
XN=σxnx+τxyny+τxznz
YN=τyxnx+σyny+τyznz
ZN=τzxnx+τzyny+σznz
(9)
εRx=εxnx+0.5(γxyny+γxznz)
εRy=εyny+0.5(γxynx+γyznz)
εRz=εznz+0.5(γyzny+γxznz)
(10)
(5)重复第(4)步,求出当前循环中所有时间点处的ε,σ,γ和τ数值,从而获得ε,σ,γ和τ的变化历史。
(6)计算疲劳寿命参量。具体采用什么参量因不同的寿命模型而异。一般而言,在候选平面上,可以得到:正应变范围Δε=εmax-εmin、剪应变范围Δγ=γmax-γmin等。无论采用何种疲劳寿命模型,均可由某种求解非线性方程的数值方法(如对分法、Newton-Raphson法等)求得相应的Nf值。
(7)由第(6)步,可求得当前平面上的损伤:
dcycle=1/Nf
(11)
(8)如果在所研究的循环中,有载荷块存在,按照前面第(4)~(8)步可以得到该载荷块内每个循环的损伤,采用线性累积损伤法则,则该载荷块内的损伤为
(12)
式中,n为载荷块内的循环次数。
(9)按照一定的角度增量(如2o)变化θR,并对每一个新的θR,也按照一定的角度增量变化θ(如2o)。这样做的目的在于搜索损伤最大的那个平面。对每一个平面的方向矢量n,重复第(3)~(8)步,求得每个平面上的dblock,在所有这些平面上找出dblock值最大的那个平面,即为临界损伤平面,并令
Dmax=(dblock)max
(13)
(10)对应的Nf值为最小寿命:
Nf=1/Dmax
(14)
此时的θR和θ值就是临界损伤平面法矢n的特征角度。上述过程很容易编程实现,此处不再赘述。
2 结果与分析
分别对某型航空发动机650 ℃条件下涡轮盘用材料ZSGH4169高温合金和980 ℃条件下涡轮转子叶片用材料DZ125定向凝固高温合金进行疲劳-蠕变实验,两类材料的实验方法均参照GB/T 15248-2008《金属材料轴向等幅低循环疲劳试验方法》严格执行。另外,根据第1.2节论述的临界面损伤方法的计算流程,结合基于Walls,Ccb,Swt,Glk,和Fin为参数的各种疲劳-蠕变寿命模型对其进行寿命预测。具体的研究内容按不同的材料分为两小节,详细研究内容如下。
2.1各向同性合金ZSGH4169
ZSGH4169高温合金取自涡轮盘C向(即弦向),其在650 ℃条件下基本力学性能如下表1所示。

表1 ZSGH4169合金650 ℃下的基本力学性能
ZSGH4169高温合金在650 ℃条件下的疲劳-蠕变性能实验数据如下表2所示。
基于Walls,Ccb,Swt,Glk,和Fin的各种疲劳-蠕变寿命模型的材料参数见表3,表4给出了ZSGH4169合金寿命预测值与实验值的相关系数。另外,图2~6给出这些参数方法与断裂循环次数Nf的关联结果。

表2 ZSGH4169合金650 ℃下的疲劳-蠕变实验结果Table 2 Experimental results of fatigue-creep of ZSGH4169 superalloy at 650 ℃
Note: “X” of “X/XX” denotes tensile dwell time, s; “XX” of “X/XX” denotes compressive dwell time, s. Similar to the present text.

表3 ZSGH4169合金各种疲劳-蠕变寿命模型的材料参数
从结果可以看出,Walls临界损伤平面作为参数的寿命模型与实验数据的关联程度最高,预测值与实验值在±3倍的分散带内;Swt参数方法和Ccb参数方法接近;Glk参数方法较差;Fin参数方法最差。

表4 ZSGH4169合金各种疲劳-蠕变寿命模型的相关系数

图2 Walls参数与断裂寿命Nf的关系Fig.2 Relationship between Walls parameter and fatigue life Nf

图3 Swt参数与断裂寿命Nf的关系Fig.3 Relationship between Swt parameter and fatigue life Nf

图4 Ccb参数与断裂寿命Nf的关系Fig.4 Relationship between Ccb parameter and fatigue life Nf
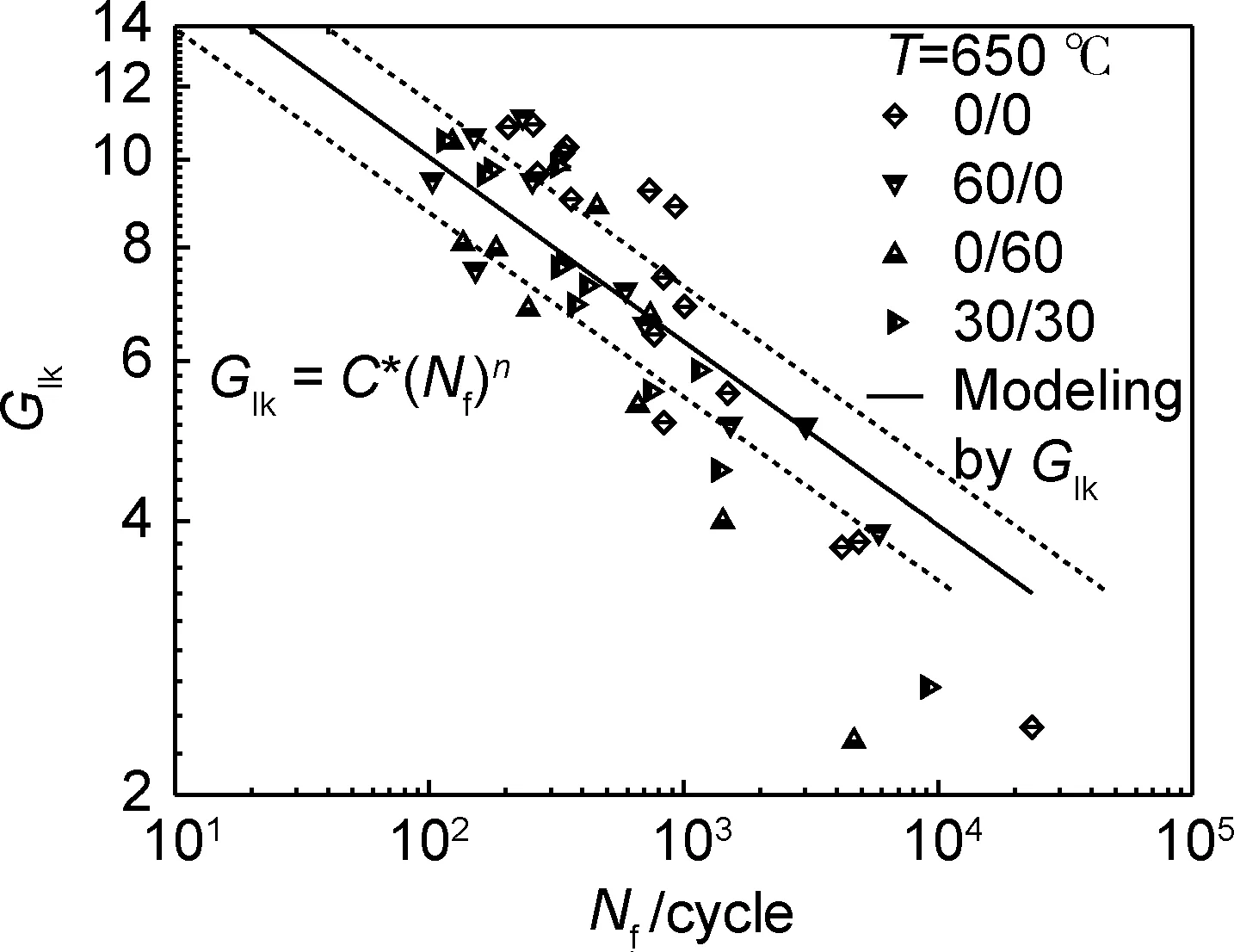
图5 Glk参数与断裂寿命Nf的关系Fig.5 Relationship between Glk parameter and fatigue life Nf
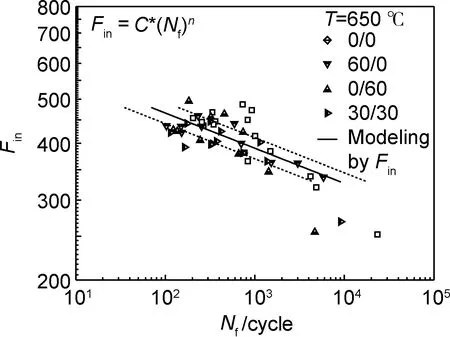
图6 Fin参数与断裂寿命Nf的关系Fig.6 Relationship between Fin parameter and fatigue life Nf
2.2定向凝固合金DZ125
DZ125高温合金取样方向为L向(即纵向),其在980 ℃条件下基本力学性能如表5所示。
DZ125高温合金在980 ℃条件下的疲劳-蠕变性能实验数据如表6所示。
基于Walls,Ccb,Swt,Glk和Fin的各种疲劳-蠕变寿命模型的材料参数见表7,表8给出了DZ125合金寿命预测值与实验值的相关系数。另外,图7~11给出这些参数方法与断裂循环次数Nf的关联结果。需要说明的是,图中的L表示DZ125合金的纵向方向。
从结果可以看出,除了Walls参数方法预测的寿命最差以外,其他几种参数方法预测的疲劳-蠕变寿命基本上位于±2.5倍分散带附近,其中Glk参数方法与实验数据的关联程度最高,其他模型预测精度由高到低依次为Ccb参数方法、Swt参数方法和Fin参数方法。

表5 DZ125合金980 ℃下的基本力学性能Table 5 Basic mechanical properties of DZ125 superalloy at 980 ℃
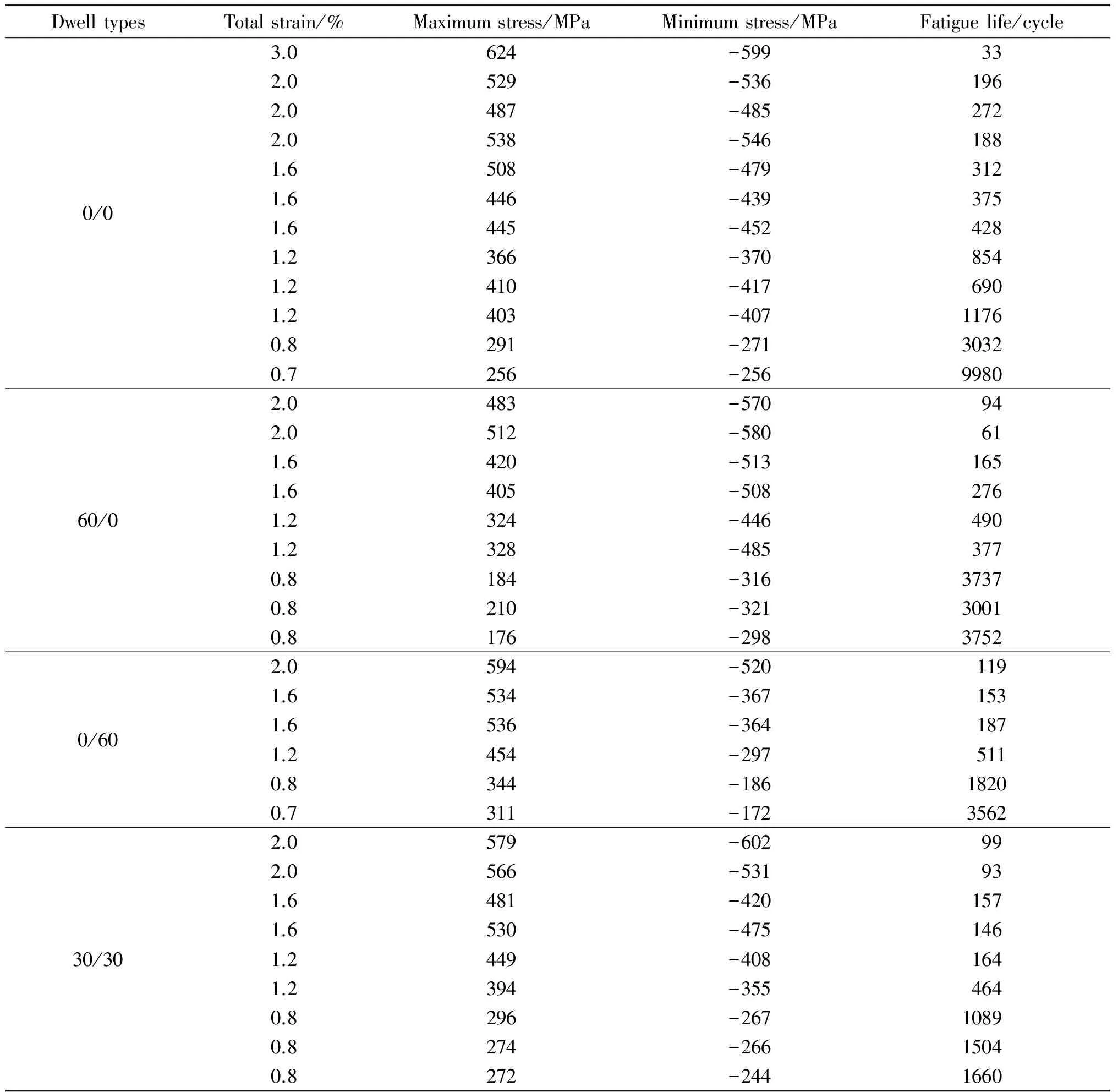
表6 DZ125合金980 ℃下的疲劳-蠕变实验结果Table 6 Experimental results of fatigue-creep of DZ125 superalloy at 980 ℃
Note: “X” of “X/XX” denotes tensile dwell time, s; “XX” of “X/XX” denotes compressive dwell time, s. Similar to the present text.

表7 DZ125合金各种疲劳-蠕变寿命模型的材料参数Table 7 Material parameters of various fatigue life models of DZ125 superalloy

表8 DZ125合金各种疲劳-蠕变寿命模型的相关系数
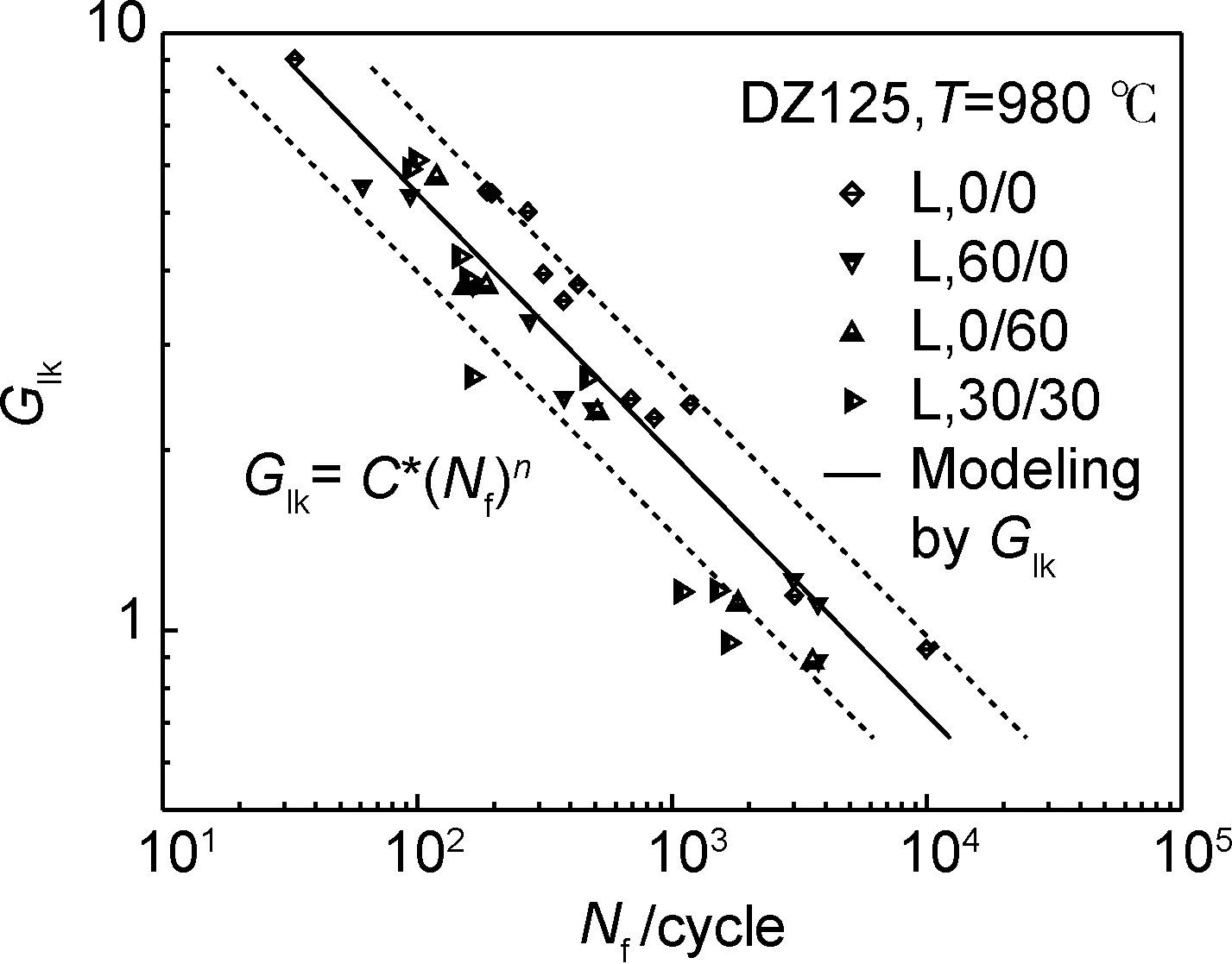
图7 Glk参数与断裂寿命Nf的关系Fig.7 Relationship between Glk parameter and fatigue life Nf
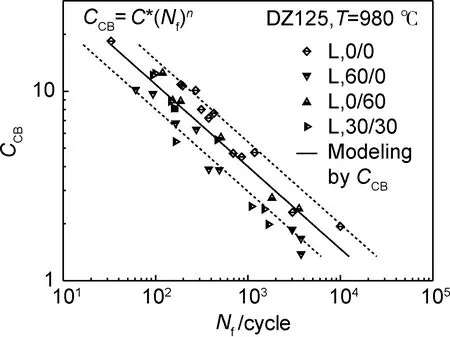
图8 Ccb参数与断裂寿命Nf的关系Fig. 8 Relationship between Ccb parameter and fatigue life Nf

图9 Swt参数与断裂寿命Nf的关系Fig.9 Relationship between Swt parameter and fatigue life Nf
3 结论
(1)对于涡轮盘用材料ZSGH4169合金,在本工作研究的几种寿命模型中,采用以Walls作为参数的寿命模型进行寿命预测要更加合适,可以获得与实验数据相关系数为0.841的结果,其预测值与实验值相比基本落在±3倍分散带以内。

图10 Fin参数与断裂寿命Nf的关系Fig.10 Relationship between Fin parameter and fatigue life Nf
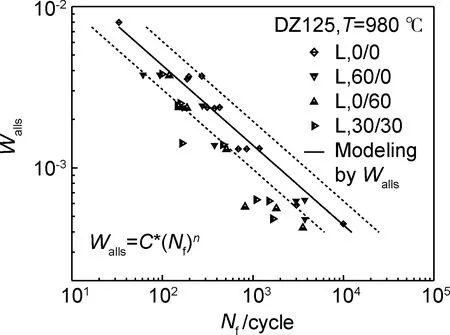
图11 Walls参数与断裂寿命Nf的关系Fig.11 Relationship between Walls parameter and fatigue life Nf
(2)对于定向凝固涡轮叶片材料DZ125合金,采用最大剪切应变能所在平面上的Glk参数,可以获得与实验数据相关系数为0.941的结果,其寿命预测值与实验值相比基本落在±2.5倍分散带以内。
(3)保载时间和平均应力对两种合金材料的高温疲劳-蠕变寿命的影响规律非常复杂,还有待于继续深入开展相关研究。
[1] 徐灏. 疲劳强度[M]. 北京:高等教育出版社,1988.
(XU H. Fatigue strength[M]. Beijing:Higher Education Press, 1988. )
[2] HUANG J, YANG X G, SHI D Q,etal. Systematic methodology for high temperature LCF life prediction of smooth and notched Ni-based superalloy with and without dwells[J]. Computational Materials Science, 2014, 89:65-74.
[3] 金丹,缑之飞. 缺口件疲劳寿命预测新方法[J]. 航空材料学报,2017,37(2):81-87.
(JIN D, GOU Z F. A new method of fatigue life prediction for notched specimen[J]. Journal of Aeronautical Materials. 2017,37(2):81-87.)
[4] DONG C L, YU H C, LI Y. Life modeling of anisotropic fatigue behavior for a single crystal nickel-base superalloy[J]. International Journal of Fatigue, 2014, 61:21-27.
[5] GUSTAVO H B D, MARCOS B C. Numerical modeling of uneven thermoplastic polymers behaviour using experimental stress-strain data and pressure dependent von Mises yield criteria to improve design practices[J]. Procedia Engineering, 2011, 10:1871-1876.
[6] GARUD Y S. A new approach to the evaluation of fatigue under multiaxial loading[J]. Journal of Engineering Materials and Technology, 1981, 103(5):118-125.
[7] FINDLEY W N. A theory for the effect of mean stress on fatigue of metals under combined torsion and axial load or bending[J]. Journal of Engineering for Industry, 1959, 81(6):301-306.
[8] BROWN M W, MILLER K J. A theory for fatigue failure under multiaxial stress and strain condition[J]. Proceedings of the Institution of Mechanical Engineers, 1973, 181(1):705-755.
[9] LOHR R D, EILLISION E G. A simple theory for low cycle multiaxial fatigue[J]. Fatigue Fracture Engineering Material Structure, 1980, 3(1):1-17.
[10] KANAZAWA K, MILLER K J, BROWN M W. Low-cycle fatigue under out-of-phase loading conditions[J]. Journal of Engineering Materials and Technology, 1977, 99(3):222-228.
[11] LEESE G E,SOCIE D. Multiaxial fatigue: analysis and experiments[M]. America: society of plastics engineers. Inc, 1989.
[12] FATEMI A, SOCIE D F. A critical plane approach to multiaxial fatigue damage including out of phase loading [J]. Fatigue & Fracture of Engineering materials & structures, 1988, 11(3):149-165.
[13] ARAKERE N K, SWANSON G. Effect of crystal orientation on fatigue failure of single crystal nickel base turbine blade superalloys[J]. Journal of engineering for gas turbines and power, 2002, 124(1):161-176.
[14] GLINKA G, SHEN G, PLUMTREE A. A multiaxial fatigue strain energy density parameter related to the critical fracture plane[J]. Fatigue and Fracture of Engineering Materials and Structures, 1995, 18(1):37-46.
[15] CONLE F A,CHU C C, Fatigue analysis and the local stress-strain approach in complex vehicular structures[J]. International Journal of Fatigue, 1997, 19(93):317-323.
[16] CHU C C. Fatigue damage calculation using the critical plane approach[J]. Journal of Engineering Materials and Technology, 1995, 117(1):41-49.
(责任编辑:张 峥)
CriticalPlaneDamageMethodforFatigue-creepLifePredictionofNickel-basedSuperalloy
DONG Chengli1,2,3, YU Huichen1,2,3
(1 Beijing Key Laboratory of Aeronautical Materials Testing and Evaluation, Beijing Institute of Aeronautical Materials, Beijing 100095, China; 2 Aviation Key Laboratory of Science and Technology on Aeronautical Materials Testing and Evaluation, Beijing Institute of Aeronautical Materials, Beijing 100095, China; 3 Science and Technology on Advanced High Temperature Structural Materials Laboratory, Beijing Institute of Aeronautical Materials, Beijing 100095, China)
Adopting the classical critical plane damage method coupling fatigue-creep life models with adequate technique modification, the life predications of ZSGH4169 superalloy at 650 ℃and DZ125 superalloy at 980 ℃ were investigated to compare the predication accuracies of the five kinds of fatigue-creep life models,i.e. based onWalls,Ccb,Swt,GlkandFin. The results of typical examples show that the fatigue-creep model based onWallsis the best for ZSGH4169 superalloy at 650 ℃,and the predicted life falls within ±3 scatter band of the test data, while the fatigue-creep model based onGlkis the best for DZ125 superalloy at 980 ℃, and the predicted life falls within ±2.5 scatter band of the test data.
critical plane damage (CPD);fatigue-creep;life prediction;directionally solidified; correlation coefficient
2016-06-16;
2016-10-23
国家自然科学基金项目(51341001)
董成利(1982—),男,博士,高级工程师,主要从事航空发动机高温结构材料及部件强度、寿命评估与有限元数值仿真研究,(E-mail)dcldong@buaa.edu.cn。
10.11868/j.issn.1005-5053.2016.000102
TG132.3+2
: A
: 1005-5053(2017)04-0069-08
