永磁同步电机改进预测电流控制

徐 楠, 吕 彦, 谢后晴

(中国矿业大学 信息与电气工程学院，江苏 徐州 221008)

永磁同步电机改进预测电流控制

徐 楠, 吕 彦, 谢后晴

(中国矿业大学 信息与电气工程学院，江苏 徐州 221008)

在模型预测控制中，大量的计算会产生动作延迟，并且离散化方法的不准确性也会将误差引入系统，当采样时间较长时上述两种情况会导致系统性能恶化。为解决该问题，可采用双线性变换法获得更为精确的电机离散时间模型，该离散方法可保证系统有更优的稳定性。再通过引入延时补偿来解决预测电流时由于计算导致的动作延迟,从而减小电流纹波。基于此搭建仿真模型并进行试验研究，仿真与试验证明该预测系统具有动态跟踪特性好、电流纹波小和抗负载扰动强等优点。

永磁同步电机； 模型预测控制； 双线性变换法； 预测电流控制； 延时补偿

0 引 言

由于具有功率密度高、结构简单、体积小及无碳刷等优点，永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)被广泛应用于调速系统中[1-3]。在航天航空、数控机床及工业机器人驱动等领域，一般对系统的动、静态性能要求较高，因此需要转矩响应快同时保证脉动较小[4-5]。电机的电磁转矩与定子电流密切相关，因此电流环的设计极其重要。目前PMSM电流环大都采用PI控制，虽方法简单易行，但由于是一线性调节器,难以兼顾系统响应的快速性和稳定性，因此，制约了其在高性能控制场合的应用[6-8]。

模型预测控制(Model Predictive Control，MPC)采用多步测试、滚动优化和反馈校正等控制策略，因此控制效果好、可迅速跟踪变化的指令信号且具有较好的鲁棒性,近年来被逐渐应用于PMSM调速系统中[9-10]。文献[11]根据电机的离散数学模型预测逆变器所产生的7个不同电压矢量中的电流部分，实现对电流的有效控制。文献[12-13]获得PMSM交直轴电压离散方程并分析PWM占空比更新方式，得到电流响应速度最快为2Ts的结论。文献[14]将无差拍控制应用于电流内环可提高电流动态响应，速度环采用预测控制，改善了系统的跟踪特性、降低了稳态误差，但存在设计过于繁杂的缺点。文献[15]提出一种用于表贴式PMSM模型预测电流控制算法，通过电流前馈和反馈控制实现了dq轴电流的有效解耦，改善了电流控制的动态性能。

上述MPC方案在实施时，需将连续域内的PMSM数学模型进行离散化，且都采用传统的前向欧拉法。这种方法虽然能简化离散化过程，但在采样时间Ts较大时，很难同时兼顾算法简便性和系统的稳定性[16]。同时，基于MPC系统在实施后，若想获得高性能，控制采样时间不能太长，而MPC控制存在运算量过大的问题，将产生动作延时，若控制器的设计未考虑该问题，所产生的延时会导致系统性能恶化[17-18]。为解决这种问题,可引入延时补偿来保证系统在较大采样周期时仍有很好的控制效果。

本文为提高PMSM调速系统的动态品质，采用MPC方法来设计调速系统的电流环。针对前向欧拉离散方法导致系统不稳定的问题，采用双线性变化法建立PMSM的离散化预测模型，进一步提高系统稳定性，加入延时补偿来解决动作延时，通过预测模型实现对逆变器所产生的7个不同电压矢量中电流部分的有效预测，选择使得代价函数最小化的一组电压矢量并用于下一采样时刻，从而实现对系统的有效控制。仿真和试验验证了该系统具有良好的电流跟踪性能和转矩特性，可获得比未加入延时补偿时更好的电流波形。

1 电机数学模型

内置式PMSM在dq旋转坐标系下的定子电流方程可写成如下形式[19]：

其中：

式中：ud、uq——d、q轴电压；id、iq——d、q轴电流；Ld、Lq——d、q轴电感；Rs——定子电阻；ωr——转子电角速度；ψf——永磁体与定子交链的磁链。

2 电机电流模型的离散

2. 1 离散化方法介绍

双线性变换法相当于数学的梯形积分法，即以梯形面积近似代替积分。这种离散方法相较于常用的前向欧拉法更为准确，稳定性更高[20]。下面针对两种离散化方法进行分析：

前向欧拉法离散化公式为

双线性变换法离散化公式为

式中：T——采样周期。

这两种不同离散化方法的s平面与z平面的映射关系如下所述。

(1) 前向欧拉法。由式(5)可得

式(6)两端同时取模平方：

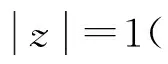
这表明只有当D(s)的所有极点位于左半平面的以点(-1/T,0)为圆心，1/T为半径的圆内，离散化后D(z)的极点才位于z平面单位圆内，意味着采用这种离散方法s平面上只有部分面积能映射到z平面单位圆内，即D(s)稳定，但D(z)不一定能稳定，需要靠减小采样周期方能保证D(z)稳定。

(2) 双线性变换法。同理，由式(6)可得

两边取模的平方，得

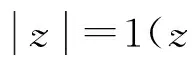
从上述分析可见，双线性变换将整个s平面左半部全部映射到z平面单位圆内，该映射关系表明若D(s) 稳定，则离散后D(z)也一定是稳定的。对比前向欧拉离散方法，采用双线性变化法离散后的系统稳定性不再受采样频率的影响。

2. 2 离散方法稳定性仿真分析

根据PMSM状态方程式(1)～式(4)，可以写出PMSM特征方程：

图1 变频率及低频率时电机极点分布图

根据电机特征方程可以做出电机极点分布图。结合电机极点分布图，对不同采样时间和不同速度给定情况下两种离散方法的稳定性进行仿真分析。

在考虑两倍额定转速情况下，分别对高频率(5 kHz，离散时间为0.000 2 s)以及低频率(500 Hz，离散时间为0.002 s)进行仿真，仿真结果如图1所示。

从仿真中可以看出，当离散时间减小后，电机在高转速下的极点分布会有超出前向欧拉法稳定圆的情况。在这种情况下，前向欧拉法将不再适用。但是，从电机极点的走势中可以看出，电机极点始终分布在左平面中，始终满足双线性变换法σ<0这一稳定性条件。因此，双线性变换法的稳定性更高。

2. 3 离散电机电流模型

利用双线性变化法对式(1)所示的电流模型进行离散，则dq参考坐标系下的电机离散电流模型如下：

3 延时补偿

补偿延时的基本思想是考虑计算时间过长导致的动作延时，对原有算法进行二次补偿。图2为进行延时补偿的预测控制算法流程图。

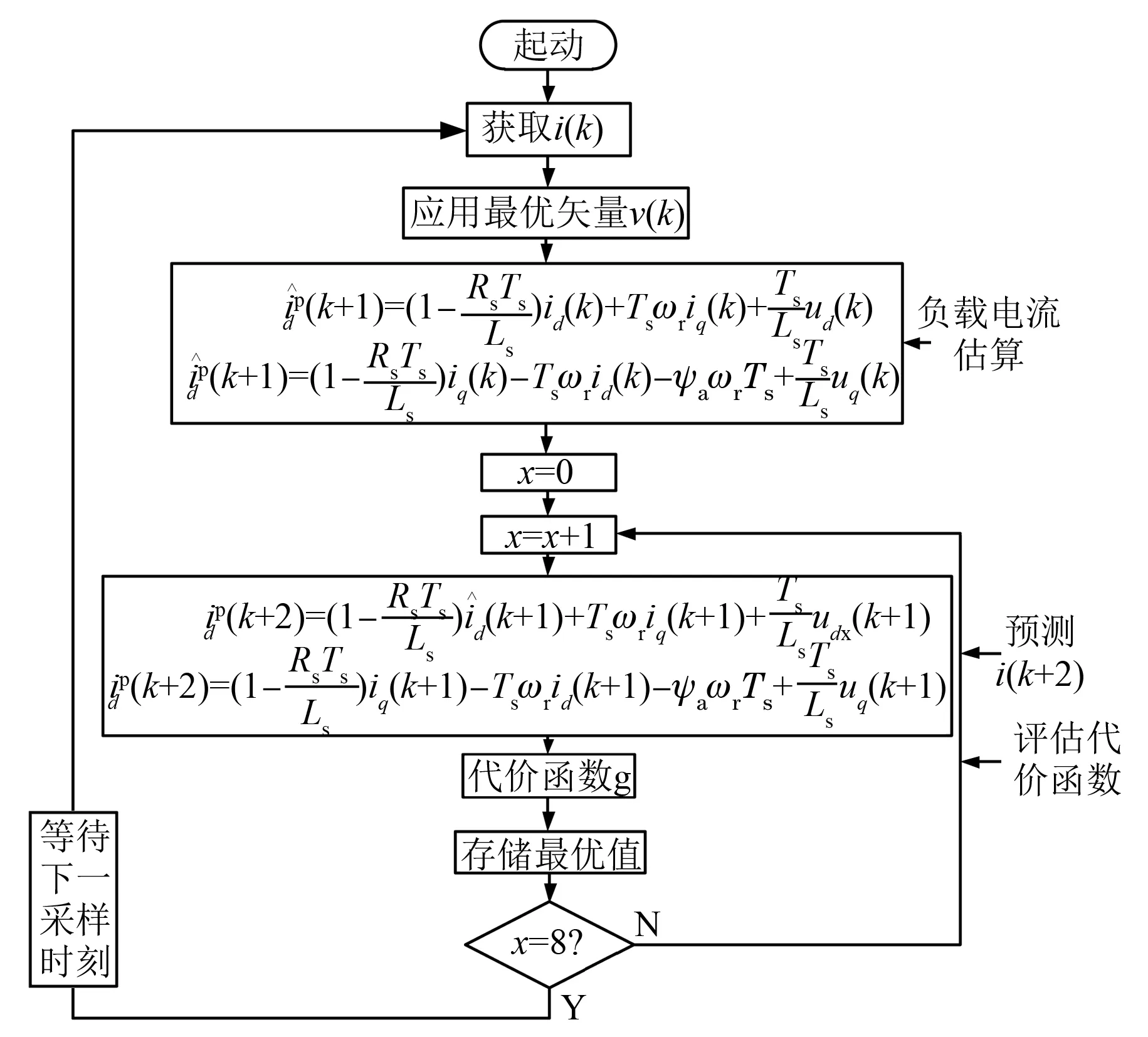
图2 加入延时补偿的预测电流控制流程图

从图2可知，该算法通过应用最优的电压矢量(k时刻)来估算k+1时刻电流值，根据k+1时刻电流估算值完成对k+2时刻的电流预测，从而实现延时补偿。

为达到转矩电流有效跟踪、优化转矩/安培比值以及限制电流幅值的控制目标，并结合延时补偿将代价函数修正为

其中：

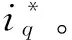
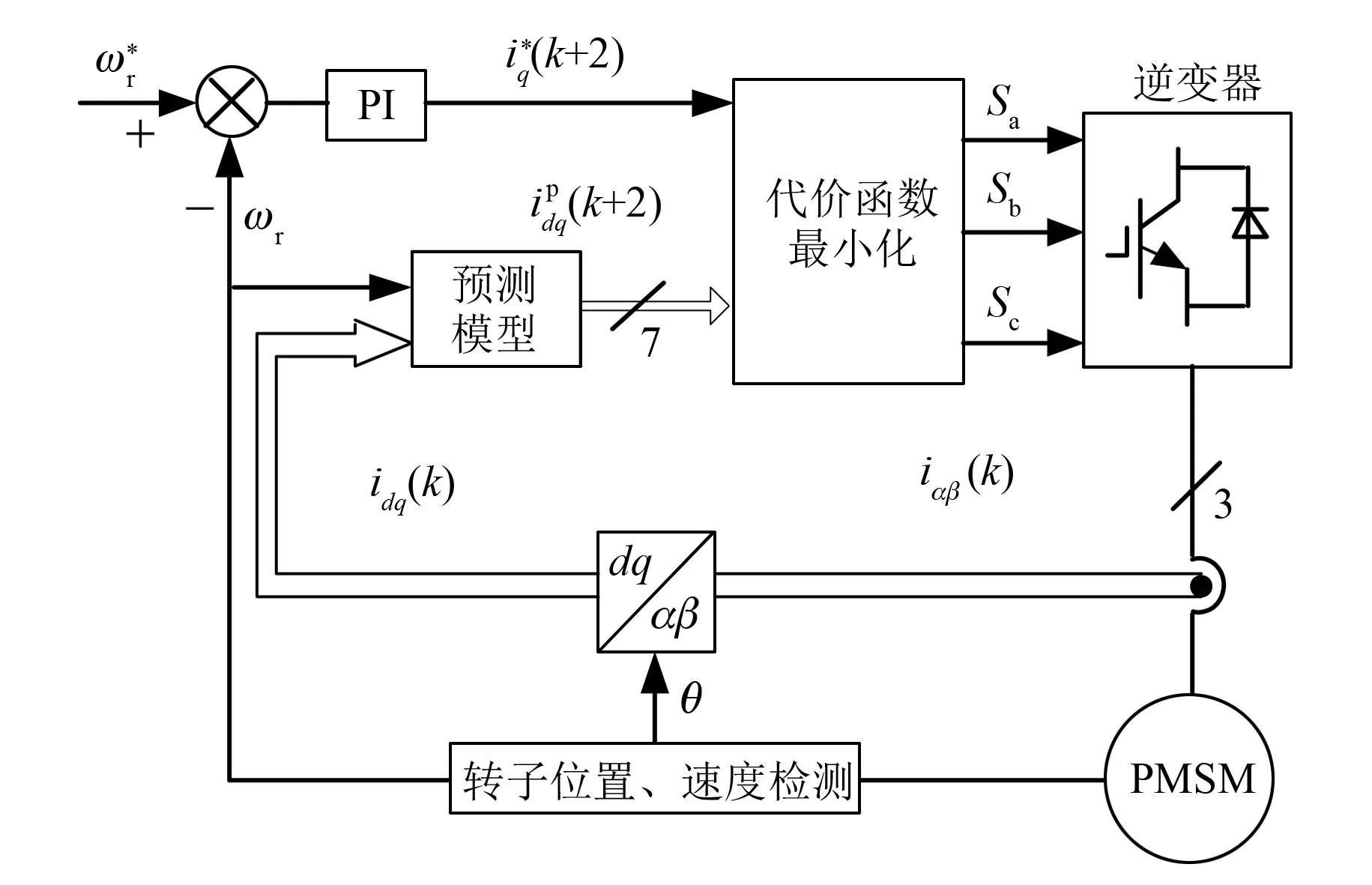
图3 PMSM预测电流控制系统框图

在整个控制系统中，电机的离散时间模型负责预测逆变器所产生的7个电压矢量中的定子电流矢量，选择能够使得代价函数最小化的电压矢量，实现对系统的有效控制。

4 仿真与试验

4. 1 仿真验证

基于图3所示的系统控制框图，建立MATLAB/Simulink仿真模型。仿真中电机参数设定参照表1所示电机实际参数。

给定速度为100 rad/s，电机带2 N·m起动，为验证系统的速度跟踪性能，在t=0.3 s时增至200 rad/s，t=0.4 s时减至50 rad/s；为验证系统的转矩抗扰动性能，在t=0.55 s时加载至额定负载6.5 N·m，在t=0.75 s时切除负载，得到图4～图7所示的仿真图。

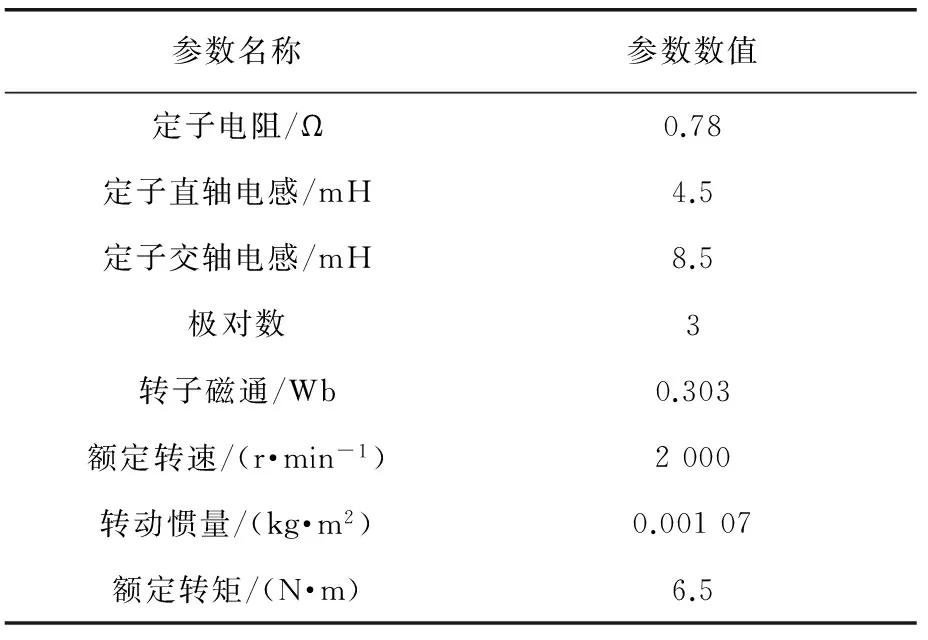
表1 PMSM参数

从图4可知，采用改进预测电流控制时转速起动超调小，给定速度发生变化时，实际的电机速度跟踪迅速，且在加/减载时速度经过短时间调整后恢复到给定值，有较好的抗扰性能。

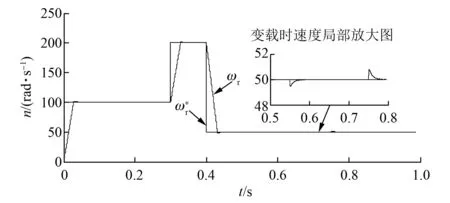
图4 改进预测电流控制下的转子速度图

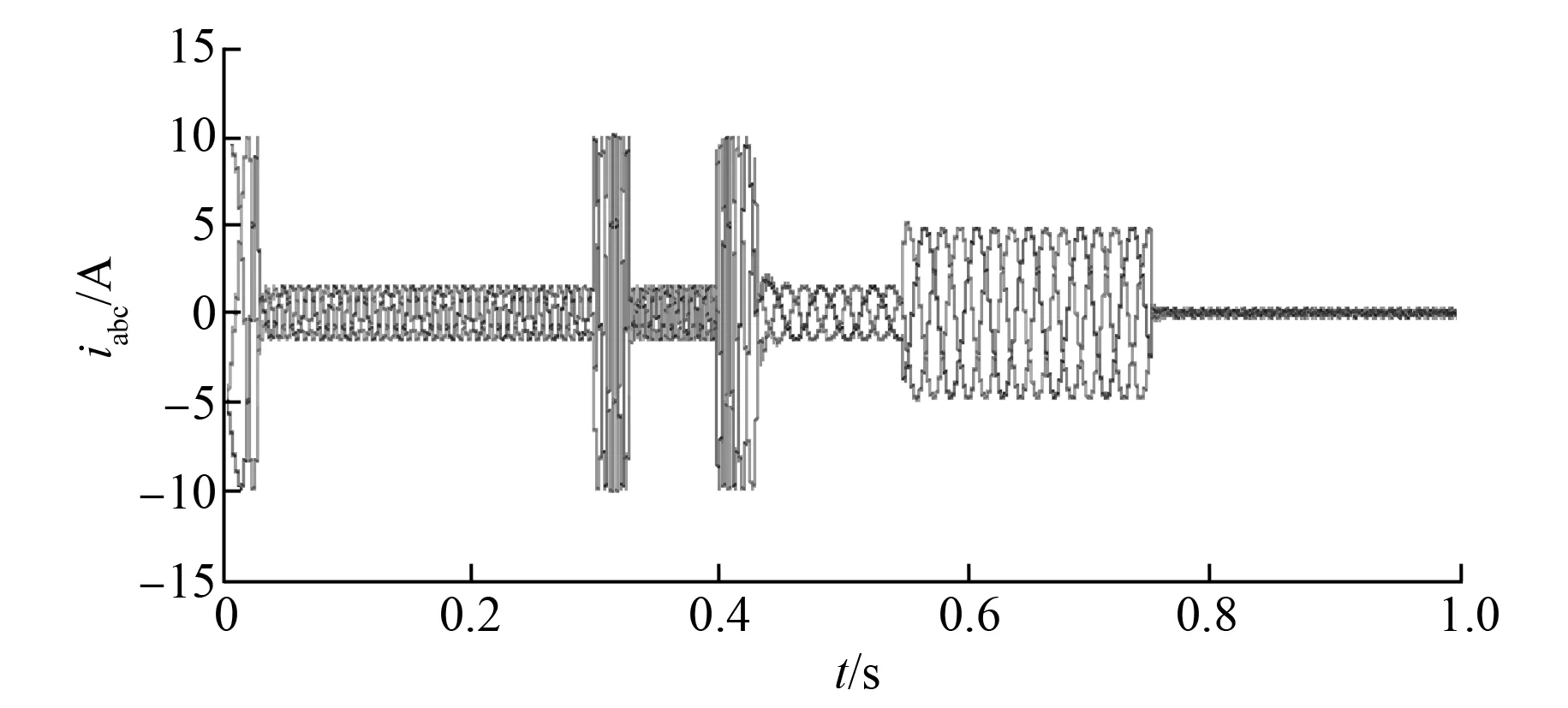
图5 改进预测电流控制下的定子电流图

从图5、图6可知，采用改进预测电流控制时，电机输出转矩脉动较小，电流纹波小，在变载时能快速到达给定值。从图7可知，当变载和变速时，q轴电流响应迅速，同时d轴电流由于代价函数的约束，维持在0附近，并未随负载变动而大幅度波动，实现了对dq轴电流的解耦。

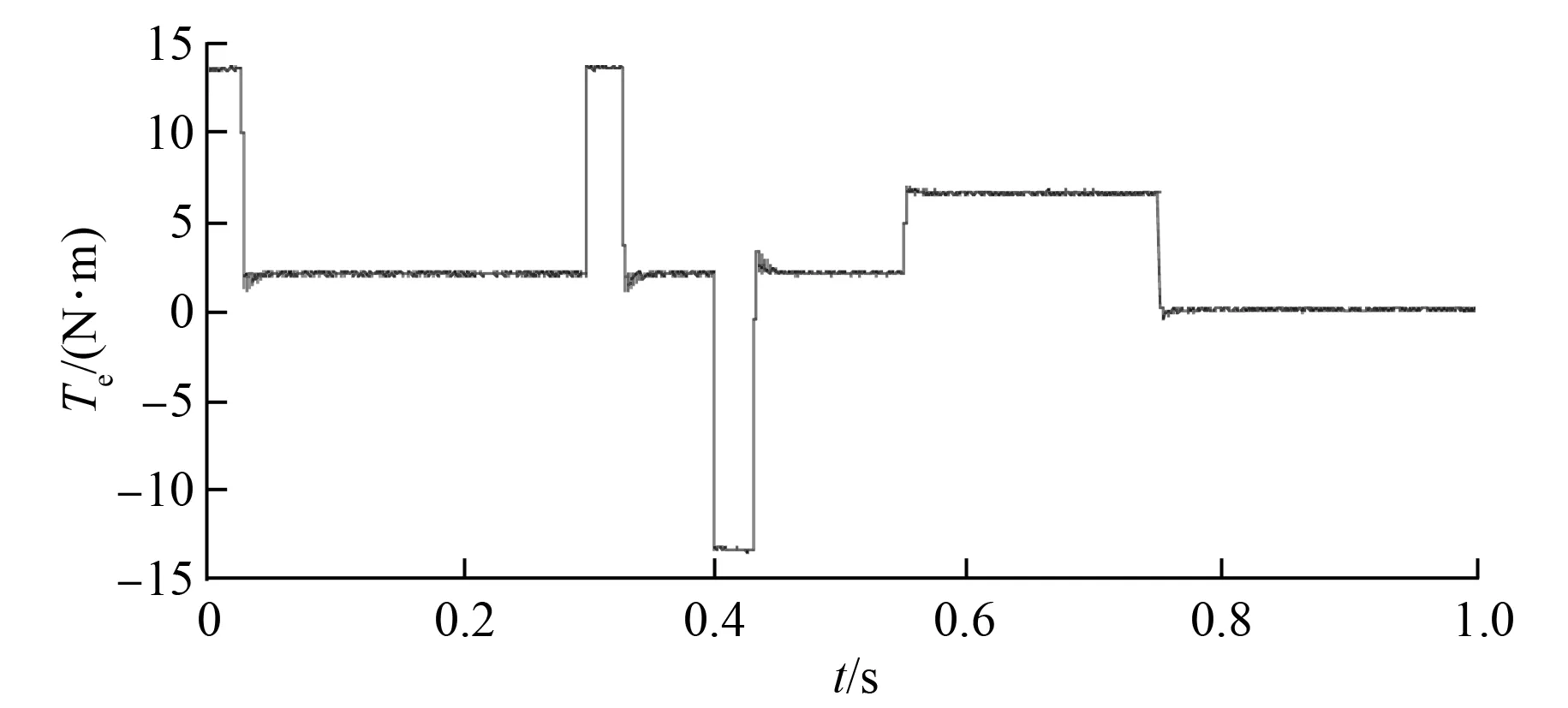
图6 改进预测电流控制下的转矩波形

图7 改进预测电流控制下的dq轴电流

为验证延迟补偿后的定子电流纹波比未进行补偿时更小，在保证与上述相同的仿真条件下，对未补偿系统也进行相应的仿真分析，波形如图8、图9所示。

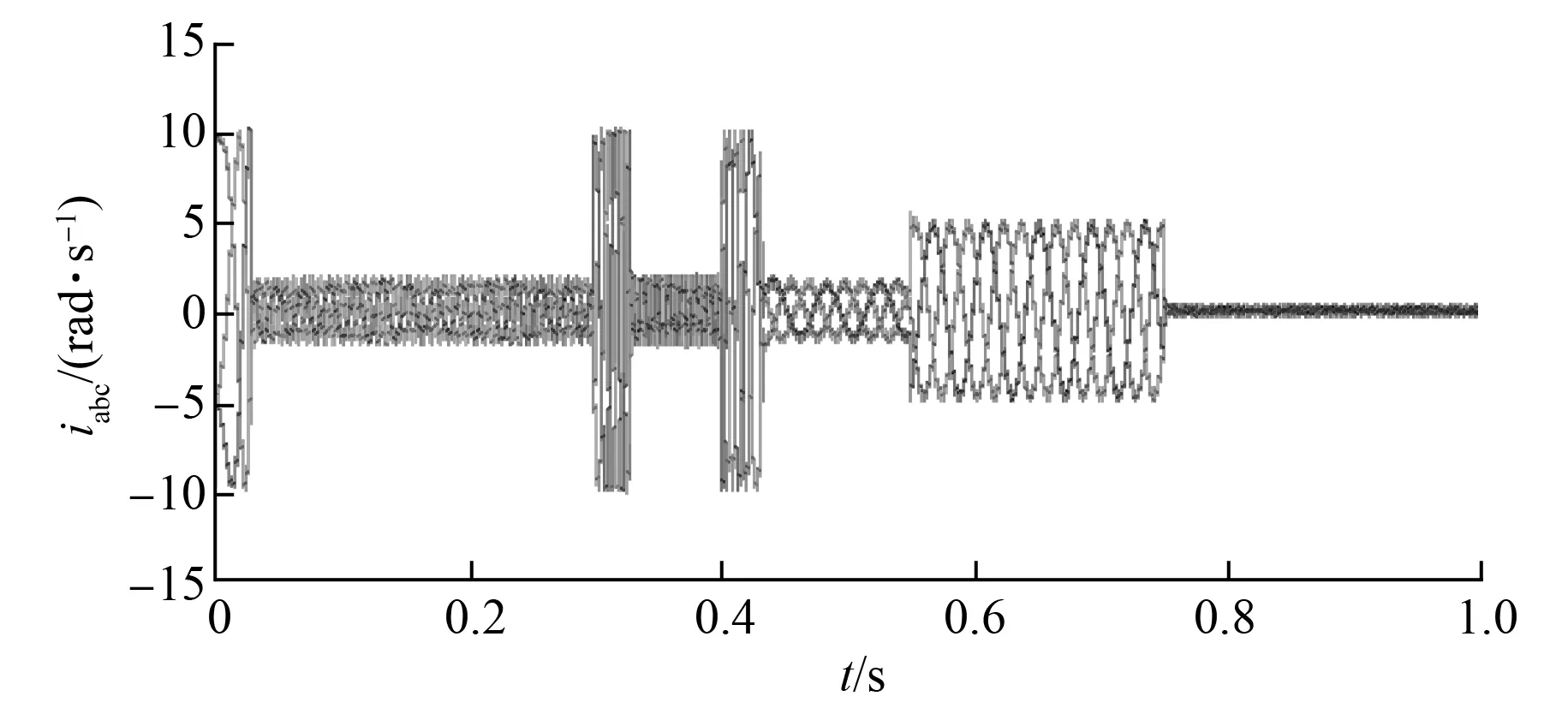
图8 未补偿时定子电流图

图9 未补偿时电机转矩波形

对比图5、图8可看出，未进行延时补偿控制下的定子三相电流的纹波较大，从而导致了图9中的电机转矩脉动较大，稳定性不如加入延时补偿后的系统。

4. 2 试验验证

试验平台由基于TMS320F28335的两电平逆变器和一套1.36 kW的内置式PMSM系统组成，如图10所示。

图10 硬件平台

试验系统与仿真研究系统的参数一致。试验主要测试改进预测电流控制系统在加减载时的动态特性，试验条件如下：电机给定速度为60 rad/s(60×9.55 r/min)，电机空载起动，经历加至额定负载6.5 N·m再减为空载的过程。试验波形如图11～图13所示。

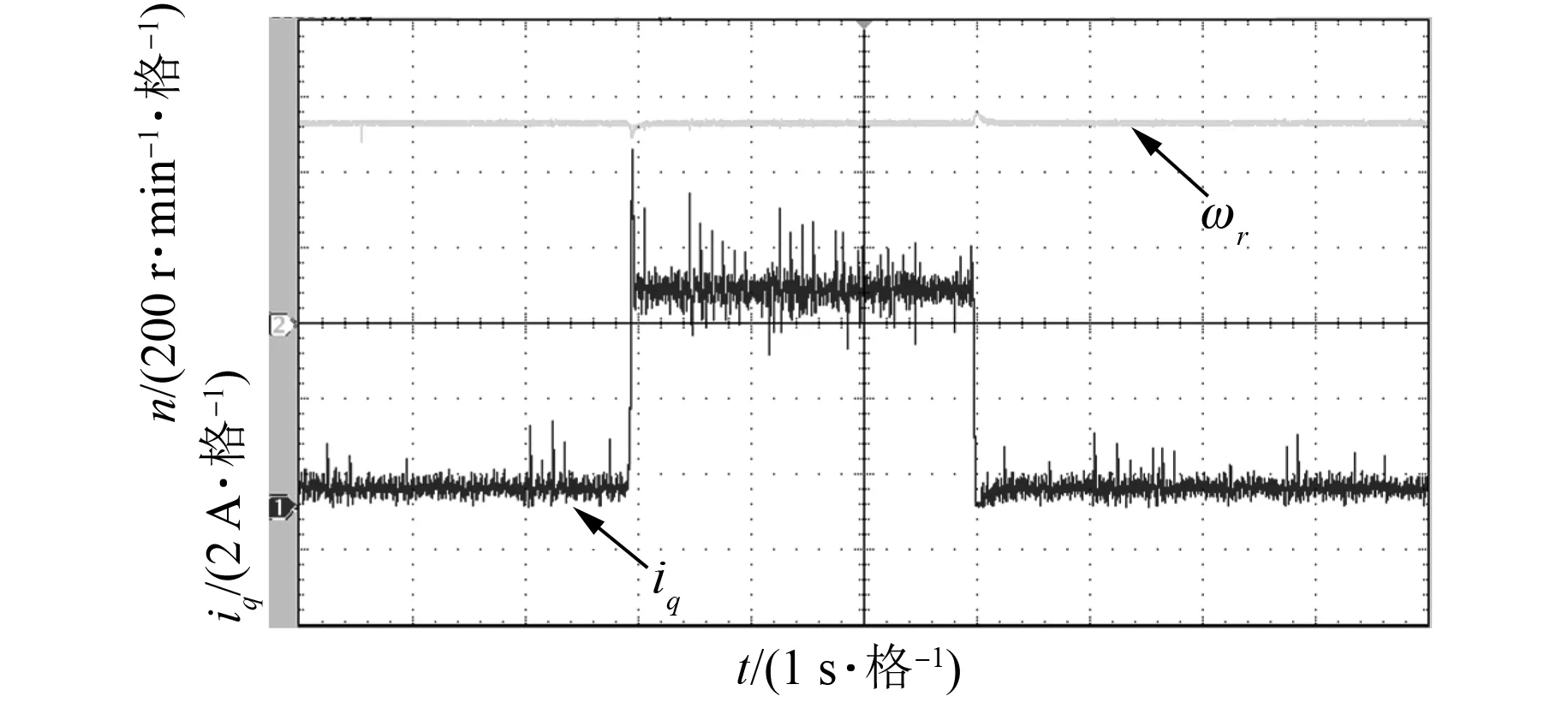
图11 变载情况转速与iq响应

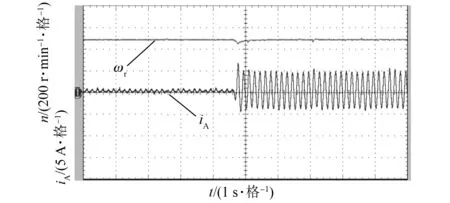
图12 加载情况转速与A相电流响应

图13 减载情况转速与A相电流响应

从图11中iq波形(q轴电流在实际测量时由于测量误差的存在，特别是试验电机容量过小导致有部分脉动)可以看出负载变化时，电流调节能够快速跟随变化，保证了转速突变少，动态过程迅速。从图12、图13可看出负载恒定时，A相电流保持恒定，当加/减载时转速与电流都经过短时间调整再次达到稳定。试验结果验证了改进预测控制系统的动态响应好和较强的抗负载干扰能力。

5 结 语

针对前向欧拉法离散后系统稳定性不高的问题，本文将双线性变化法应用于PMSM数学模型的离散化处理上，可以使得电机的预测控制系统具有更优的稳定性。同时，为改善MPC因计算量过大而存在的动作迟滞问题，引入延时补偿。搭建PMSM改进预测电流控制模型，并做了仿真研究。结合试验室硬件平台，进行相应试验验证，仿真与试验结果证明该预测系统具有明显改善调速系统动态品质、降低电流谐波、对外部干扰不敏感等优点。

[1] 李永东,张猛.高性能交流永磁同步电机伺服系统现状[J],伺服控制,2008(1): 34-37.

[2] 唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,1997.

[3] 陈荣.永磁同步电机控制系统[M].北京:中国水利水电出版社,2009.

[4] 郭庆鼎,孙宜标,王丽梅.现代永磁电动机交流伺服系统[M].北京:中国电力出版社,2006.

[5] 王伟华,肖曦,丁有爽.永磁同步电机改进电流预测控制[J].电工技术学报,2013,28(3): 50-55.

[6] 符慧,左月飞,刘闯,等.永磁同步电机转速环的一种变结构PI控制器[J].电工技术学报,2015,30(12): 237-242.

[7] 朱磊,温旭辉,赵峰,等.永磁同步电机弱磁失控机制及其应对策略研究[J].中国电机工程学报,2011,31(18): 67-72.

[8] 谢玉春.交流永磁同步电机伺服系统控制策略研究[D].哈尔滨:哈尔滨工业大学,2011.

[9] 何栋炜,彭侠夫,蒋学程.永磁同步电机模型预测控制的电流控制策略[J].哈尔滨工程大学学报,2013,34(12): 1556-1565.

[10] 高丽媛.永磁同步电机的模型预测控制研究[D].杭州:浙江大学,2013.

[11] FUENTES E, RODRIGUEZ J, SILVA C, et al. Speed control of a permanent magnet synchronous motor using predictive current control[C]∥IEEE 6th International Power Electronics and Motion Control Conference, IPEMC'09, 2009: 390-395.

[12] HYUNG T M, HYUN S K, MYUNG J Y. A discrete-time predictive current control for PMSM[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 464-472.

[13] FLORENT M, LINSHI X F, JEAN M R, et al. A comparative study of predictive current control schemes for a permanent-magnet synchronous machine drive[J]. IEEE Transactions on Industrial Electronics, 2009, 56(7): 2715-2728.

[14] 邱忠才,肖建,郭冀岭,等.永磁同步电机预测控制[J].电力电子技术,2015,49(8): 73-75.

[15] 王东文,李崇坚,吴尧,等.永磁同步电机的模型预测电流控制器研究[J].电工技术学报,2014,29(1): 73-79.

[16] 王勃,于泳,孙伟,等.基于改进离散全阶磁链观测器的感应电机矢量控制[C]∥中国电工技术学会电力电子学会学术年会,2014.

[17] BARROS J D, SILVA J F A, JESUS E G A. Fast-predictive optimal control of NPC multilevel converters[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 619-627.

[18] JOSE R, PATRICIO C.功率变换器和电气传动的预测控制[M].陈一民,周东华,卫三民,等译.北京:机械工业出版社,2014.

[19] 杨国良,李建雄.永磁同步电机控制技术[M].北京:知识产权出版社,2015.

[20] 高金元源,夏洁.计算机控制系统[M].北京:清华大学出版社,2007.

Improved Predictive Current Control of Permanent Magnet Synchronous Motor

XU Nan, LÜ Yan, XIE Houqing

(School of Information and Electrical Engineering, China University of Mining and Technology, Xuzhou 221008, China)

In model predictive control system, the large amount of calculation could lead to action delay and the error would be introduced to system due to the inaccuracy discrete method. Under the condition of large sample time, the two conditions above would lead to a bad performance of the system. To solve the problem, the bilinear transformation method was taken to obtain a more accurate discrete model of motor. And this discrete method could guarantee the stability of system. Delay compensation was introduced to the system to reduce the current ripple due to the problem of action delay. Simulation and experiment results showed that the predictive system above had the advantages of better dynamic track performance, little current ripple and strong resistance to load disturbance.

permanent magnet synchronous motor (PMSM); model predictive control (MPC); bilinear transformation; predictive current control; delay compensation

徐 楠(1992—)，女，研究方向为永磁同步电机传动控制系统。

TM 351

A

1673-6540(2017)07- 0042- 06

2016 -08 -22