排课问题的数学模型研究
2017-08-07陈辉,何军
陈 辉,何 军
(安徽商贸职业技术学院 教务处,安徽 芜湖 241002)
排课问题的数学模型研究
陈 辉,何 军
(安徽商贸职业技术学院 教务处,安徽 芜湖 241002)
通过对排课问题中课程、班级、教师和场地的约束条件进行数学抽象,将排课方案的优化表示为场地利用情况和课时安排合理性的评价,给出了一个较为精炼的排课问题数学模型,在一定的问题规模下,得到了较好的排课效果。在此基础上,针对高校排课实际应用场景,基于贪心算法给出了排课问题的一种高效的近似求解方案,为基于排课的教务管理信息系统的构建提供了参考借鉴。
排课问题;排课算法;整数规划模型;贪婪算法;Lingo
排课涉及班级、教师、教学场地和各种教学资源的调配,是教学管理中复杂性最高、难度最大的问题。人们一直都在尝试利用计算机信息手段来实现自动排课。早在1962年Gotlieb即在其著作“The Construction of Class-Teacher Time Tables”中研究了排课问题的数学模型[1],并将其视为组合规划问题进行相应地深入研究。S.Even等在1976年完成了运筹学中时间表问题(Timetable Problem,TTP)的复杂度分析研究,并首次证明排课问题作为时间表问题的具体应用,是“多项式复杂程度的非确定性问题(NP完全问题)”[2]。随着90年代计算机技术的逐渐普及,课表的计算机编排开始大量出现,但由于问题本身的复杂性,在高校这样复杂的教学场景中,计算机通常只是作为手工排课的辅助手段。直到Paecher等通过对时空排列和布局寻找,找到了处理时间表问题的一些方法[3]。近年来,随着遗传算法、模拟退火算法、蚁群算法等智能算法的兴起,国内学者对排课问题投入了大量的研究[4-10],在取得丰富成果的同时,也存在着普遍的问题。以遗传算法为例,虽然经过多次迭代可以获得较好的解,但在实际应用过程中由于过多的约束条件,可能会出现两个较好的父代经过交叉后产生较差的子代,导致其对可行解的搜索能力较贪婪算法并没有突出的优势。从现实意义上说,排课问题首先关注的是在合理的时间内快速有效地给出可行解,然后尽可能地满足一系列特定条件。智能算法在处理诸如排课问题这类约束条件很多的强约束规划问题方面,还有待进一步研究。
通过对排课问题进行数学抽象,采取适当的技巧,实现了易于求解的排课问题数学模型的构建。并在此基础上,给出了关于排课问题的一种高效的贪婪搜索算法。
1 排课问题的数学模型
排课问题需要在满足资源独占性的硬性约束条件(时间、教师、教室不会冲突)下,尽可能满足特定的(排课时间均匀、课程优先时间段等)软性约束条件的情况下,使得教学资源尽可能充分使用。
1.1 变量表示
1)教学课程元集合M:其主要包含课程名称、授课教师、周学时和班级人数等,设有m个教学课程元。典型的教学课程元和教学场所元,具体如表1所示。

表1 教学课程元示例
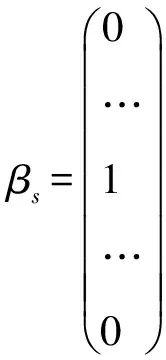
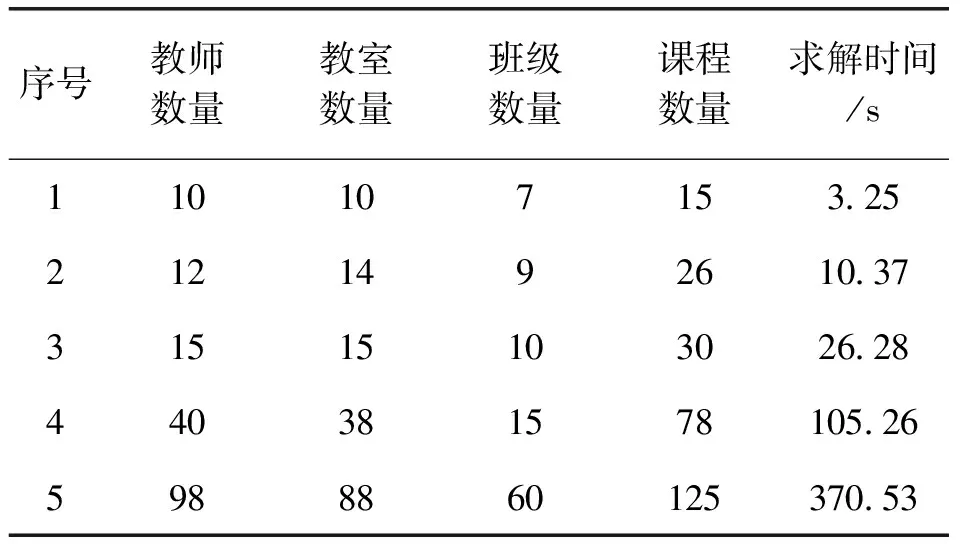
其中,Mi={M1,…,Mi,…,Mm}为所有课程构成的集合,共有m条记录,并且按课程上课班级|c(Mi)|=|βs|人数从大到小排列;函数c(·)用来映射课程元素Mi所指定的班级为βs;函数h(·)用来映射课程元素Mi所指定的教师为αk。Wi表示课程Mi对授课场所的要求标准,这种标准已经按从低到高排序,比如,W1:普通教室 2)教学场所元集合N:其主要包含校区名称、楼宇名称、教室名称、教室类型和教室可容纳人数(多少个座位或多少台机位等),这里设有n个教学场所元,N={Nj|j=1,2,…,n}。 3)授课时间元集合T:其主要定义的是教学时间段,按照现有模式每天分为上午1-2节、上午3-4节、下午1-2节、下午3-4节和晚上共计5个时间段,并按每周的时间顺序编码,每周共有25个授课时间元。为了方便排课算法的求解,将单双周合并计算,共50条记录,T={Tt|t=1,2,…,50}。比如T1表示单周周一上午1-2节课,T5表示单周周一晚上9-10节课,T30表示单周周五晚上9-10节课,T32表示双周周一上午3-4节课等等,依次类推。这样做虽然可能会在教学资源紧缺的情况下导致某门课程在单双周的上课地点与时间不同,但却形成了极为灵活的排课方式,排课模型的可行解空间得到了极大的推广,只要教学资源没有出现过于匮乏的情况,一般都能成功排课。在用穷举贪婪方式搜索排课方式的时候,也可以在条件允许的情况下优先将单双周上课安排在相同的地点与时间上。 6)根据以上表述,可以将课程Mi的排课结果Ri⊂N×T表示为教学场所和时间段之间的有序元素对(Nj,Tt)构成的集合,即课程Mi被安排在Nj教室在Tt时间段进行两个课时的教学。排课结果Ri由若干个有序元素对(Nj,Tt)构成。 7)使用rijt表示排课决策变量,其含义为 由此,可以将排课结果表示为 Ri={(j,t)|xijt≠0},i=1,2,…,m (1) 1.2 约束条件 1)硬约束条件 ①课程Mi的课时总量约束 (2) 其中,i=1,2,…m。 ②场地容量约束 ∀(j,t)∈Ri,|Nj|≥|c(Mi)| (3) 其中,|Nj|和|c(Mi)|分别用来表示教室和班级的学生容量,i=1,2,…,m。 ③资源时间独占 场地时间独占可以表示为: (4) 对任意的时间段和场地,j=1,2,…,n,t=1,2,…,50,保证场地在所有课程排课中不会产生时间冲突。 教师时间独占可以表示为: (5) 对任意时间段t=1,2,…,50,保障全院各教师(αk是列向量)所在的各行,在所有的排课结果中不会出现两次(求和小于1),即保证教师在排课中不会出现时间冲突。 班级时间独占可以表示为: (6) 对任意时间段t=1,2,…,50,保障全院各班级(βs是列向量)所在的各行,在所有的排课结果中不会出现两次(求和小于1),即保证班级在排课中不会出现时间冲突。 ④教室类型要求 ∀(j,t)∈Ri,L(Nj)≥Wi (7) 其中,对任意课程Mi,i=1,2,…,m,排给他的教室Nj的类型标准L(Nj)大于课程Mi的上课要求Wi。 2)软约束条件 对教学课程元集合M和教学场所元集合N的自身限制条件和要求视为多维约束,例如某老师要求周三上午3-4节(授课时间元集合T)在笃学楼207(教学场所元集合N)上《计算机网络基础》课(教学课程元集合M),在算法求解的过程中可以将其定义为教学课程Mi的子属性si,并用编码形式标记软约束条件。因为软约束最终未必一定需要实现,所以从原则上只要Ri尽可能满足Si即可,i=1,2,…,m。 3)目标函数 任何满足上述约束条件的可行解都可以对于一种排课方法、不同排课方法的优劣通过使用目标函数来评价。在模型求解的过程中,尽可能优化的解会对排课方法(可行解)进行优化。这里考察的目标函数由两部分构成。 ①均匀排课 相同课程的排课结果Ri在时间元集合T中尽可能分散,即方差 (8) 尽可能大。 ②可利用资源 通常使剩余场地的容量总和尽可能大的可行解,视为最优解[11]。换言之,最优解是使未分配的场地容量之和最大的可行解 (9) 其中,|Nj|用来表示教室的学生容量。 综上,排课问题可以表示为下述整数线性约束的多目标规划模型: (10) 其中,j=1,2,…,n,t=1,2,…,50,i=1,2,…,m。 1.3 优化模型的求解 对于问题规模较小的,比如教室、班级和教师数量在100以下的排课问题,上述建立的整数规划模型,在软约束条件适当简化的情况下,可以直接使用Lingo求解。在配置为CPU i7 4790,内存32GB的PC下,使用Lingo 11,得到部分计算结果如表2所示。 表2 排课优化模型的求解 对于更大规模的排课问题,在数学表述和Lingo语言的模型构建上并没有太多差异,但由于变量个数随着问题规模大幅度上升(教室、班级和教师数量大于100时,Lingo显示的变量总数在百万以上),很难在有限的时间内给出模型的解。 为解决这种困难,采用两次贪心选择:先在M中选未处理且上课人数最大的课程,再在N中选min{场地容量:场地容量≥上课人数}且符合课程要求(硬、软约束条件)的教学场地,这样可以使得教学资源的利用尽可能地高效,剩余场地的容量总和尽可能大。在满足贪心搜索的退出条件:剩余周学时为0,则教学资源尚有余量时,认为在尽可能优化的前提下找到了可行解,即排课成功。 2.1 辅助空间 1)教师资源独立标记二维数组HT=H×T,表示教师和50个授课时间元的笛卡尔乘积,用来标记教师是否在对应时间段被排课占用; 2)班级资源独立标记二维数组CT=C×T,表示教学班级和50个授课时间元的笛卡尔乘积,来标记班级是否在对应时间段被排课占用; 3)场地资源独立标记二维数组NT=N×T,表示n个教学场所和50个授课时间元,若NT(j,t)=1,则表示N中j教室在T中Tt时间段被排课。 2.2 算法描述 1)数据预处理 ①将教学课程元集合M按照班级人数进行降序排列(从大到小); ②将教学场所元集合N按照教室可容纳人数进行升序排列(从小到大)。 2)处理手工排课 一些特殊的情况,可以事先将特定需求的课程进行手工排课,即课程Mi的排课结果Ri在排课初始时就不是空集。 对M中元素Mi做遍历操作:\课程元素循环开始 判断Ri是否为空,若Ri不空,则判断下式是否成立。 (11) 若返回值为真,则报错信息“手工排课课程课Mi时总量有误!”,否则执行下述操作: 对Ri的所有排课结果元素(j,t)循环:\Ri排课结果元素(j,t)循环开始 若HT(h(Mi)t)=1,则报错信息“手工排课课程Mi在Tt时间段的任课教师h(Mi)冲突!”,否则标记HT(h(Mi)t)=1; 若CT(c(Mi),t)=1,则报错信息“手工排课课程Mi在Tt时间段的班级c(Mi)冲突!”,否则标记CT(c(Mi)t=1; 若NT(j,t)=1,则报错信息“手工排课课程Mi在Tt时间段的场地Nj冲突!”,否则标记NT(j,t)=1. \Ri排课结果元素(j,t)循环结束 \课程元素循环结束 手工排课成功。 3)贪心算法排课 接第一步1),重新对M中元素Mi做遍历操作:\课程元素循环开始 对Xi进行判断,若Xi=0,则表示课程Mi已经完成排课,返回循环; Xi>0,则: 对T中元素Tt做遍历操作和任意容量大于Mi上课人数的且类型达到Mi要求的场地Nj循环:\时间与场地循环开始 如果时间段Tt与场地Nj满足Si要求且与Ri中已有的时间间隔大于5(间隔1天),则执行: 若HT(h(Mi)t)、CT(c(Mi)t)、NT(j,t)取值都为0: 设置HT(h(Mi),t)=1,CT(c(Mi),t)=1,NT(j,t)=1; 并从课时数总量中减去2,即Xi=Xi-2; 并将排课结果添加到课程Mi中,即Ri=Ri∪{(j,t)} \时间与场地循环结束 如果时间与场地循环结束时,Ri未能扩充,Xi没有减小,表示Mi课程本轮排课失败,则舍弃(j,t);满足Si要求的判断,重新开始本轮时间与场地循环。\课程元素循环结束 根据实际情况,只要教学资源没有出现过于匮乏的情况,一般循环4-6次就能成功完成排课。但若仍有Xi>0的课程,则表示排课失败,需要根据教师或教学场地重新调整课程元素重新开始。 首先将高校排课问题描述为整数线性约束的多目标优化模型,给出了排课问题的完整数学描述,在一定复杂度规模内得到了较好的效果,得到了排课问题的一种完整、精炼的数学抽象,为排课问题的求解算法研究提供了理论基础;同时,给出了一种基于贪心算法的排课问题近似求解方案,可以快速有效地得到较好的排课结果,为教务排课管理信息系统建设提供了借鉴参考。 [1]Gotlieb CC.The construction of class-teacher timetables[J].Proc.IFIP Congress ,1962: 73-77. [2]S.Even , A.Itai , A.Shamir.On the complexity of timetabling and multicommodity flow problems[J].SIAM Journal of Computation,1976(4):691-703. [3]B.Paechter,H.Luchian,A.Cumming,et al.Two solutions to the general timetable problem using evolutionary methods[C]// IEEE Conference on Evolutionary Computation,Piscataway,NJ,Orlando,1994,1:300-305. [4]Edmund K.Burke,Dave Elliman,and Rupert F.Weare.A Hybrid Genetic Algorithm for Highly Constrained Timetabling Problems[C]//In Proceedings of the 6th International Conference on Genetic Algorithms,Larry J.Eshelman (Ed.).Morgan Kaufmann Publishers Inc.,San Francisco,CA,USA,1995: 605-610. [5]Wilke P.,Grobner M.,Oster,N.A hybrid genetic algorithm for school timetabling[J].In: McKay B.,Slaney J.(eds) AI 2002: Advances in Artificial Intelligence.AI 2002.Lecture Notes in Computer Science,2002,2557:455-464. [6]崔 妍,王 权,王 康,等.排课问题的数学模型[J].沈阳工程学院学报:自然科学版,2016,12(03):276-278,288. [7]李建丽.基于遗传算法的排课系统研究[D].黑龙江:哈尔滨工程大学,2009. [8]王 茹.基于遗传算法的排课系统关键技术研究与实现[D].吉林:吉林大学,2013. [9]赵惠怡.基于蚁群算法的排课问题的研究[D].辽宁:大连海事大学,2007. [10]李玉吉,卢才武,刘 冠.蚁群遗传算法在高校智能排课系统中的应用[J].现代电子技术,2010(14):121-123. [11]朱凤娟,王 微,赵亚莉.广义强向量拟均衡问题组的解的存在性[J].渤海大学学报:自然科学版,2015,36(2):101-105. (责任编辑魏静敏校对张凯) MathematicalModelResearchonCourseScheduling CHEN Hui,HE Jun (Office of Teaching affairs ,Anhui Business College of Vocational Technology,Wuhu 241002,Anhui Province) The constraints of courses,classes and teachers are given by mathematical abstraction in course scheduling problems,which will optimize the course scheduling scheme to provide more remaining teaching venues and make course scheduling more reasonable,that is a more refined mathematical model of timetabling problem.As the scale of the problem is not too large,the model achieves effective results.On this basis,according to the actual application of University timetabling scene,an efficient approximate solution was proposed to solve the scheduling problem based on the greedy algorithm,which provided reference for the educational management information system. Course scheduling problem; Scheduling algorithm; Integer programming model; Greedy algorithm; Lingo 2017-03-20 安徽省高等教育振兴计划项目(2014zdjy168);安徽省质量工程项目(2015mooc154) 陈 辉(1983-),男,安徽淮南人,讲师,硕士。 10.13888/j.cnki.jsie(ns).2017.03.014 TP301.6;O221 : A : 1673-1603(2017)03-0273-05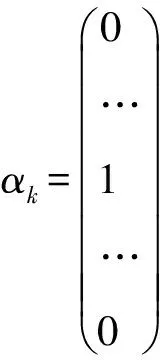
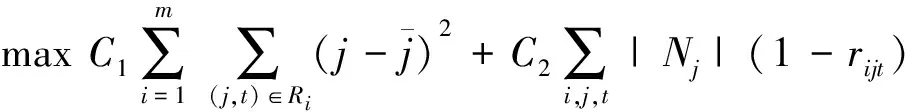
2 贪心排课算法的描述
3 结 论
