独塔部分斜拉桥动力特性的参数分析研究
2017-08-07
(福建永福电力设计股份有限公司,福州350000)
独塔部分斜拉桥动力特性的参数分析研究
■游先辉
(福建永福电力设计股份有限公司,福州350000)
本文以莆田仙港独塔部分斜拉桥为工程背景,建立基准有限元模型,研究结构7个主要参数对独塔部分斜拉桥的动力特性的影响情况,揭示独塔部分斜拉桥的动力特点。研究成果可做为独塔部分斜拉桥进行抗震设计参数选择及优化供应参考。
独塔部分斜拉桥动力特性参数分析
1 引言
部分斜拉桥是一种新型桥梁体系,其受力性能兼具连续梁桥与斜拉桥的特点。部分斜拉桥结构体系多变,具有刚柔相济的特点,跨越能力强。由于部分斜拉桥的概念较迟被提出,国内目前关于部分斜拉桥的理论研究成果不多,尤其缺乏对该桥梁结构体系动力性能较系统研究工作,相比斜拉桥和连续梁桥的研究则较多。综合国内外的研究现状看,尽管经过了20多年的研究,部分斜拉桥的研究内容在静力性能方面较集中,有了一定的研究与认识,但关于动力特性的研究还处于对具体桥梁个案分析阶段,缺乏对部分斜拉桥体系动力性能的系统性研究。
本文以现有的研究工作为基础,以独塔部分斜拉桥为研究对象,研究和归纳国内外实桥特征参数,建立独塔部分斜拉桥体系的基准有限元模型,通过改变斜拉索间距、无索区长度、斜拉索布置形式、主塔高跨比、主梁高跨比、墩高和两跨跨径比等体系参数,进行参数分析,研究结构参数变化对该类型桥梁结构动力特性的影响,揭示影响较大的主要结构参数和影响规律。
2 动力分析基准有限元模型
本文以福建莆田仙港大桥为工程背景,结合实际情况,建立空间有限元动力分析模型,利用有限元软件对该独塔双索面部分斜拉桥进行参数分析。桥型立面布置:桥梁主跨为60m+60m独塔扇形双索面部分斜拉桥,主跨全长120m,引桥长度约500m,桥梁宽16.25m。主桥的桥型立面图如图1所示。
本文采用专业的桥梁工程分析计算软件MIDAS CIVIL创建莆田仙港大桥的有限元模型。模型的模拟以抓住主要影响因素和放松次要的影响因素为核心,考虑合理的计算分析精度与计算工作量[1]。本文将计算模型进行合理简化[2][3][4],得到的空间有限元模型如图2所示。
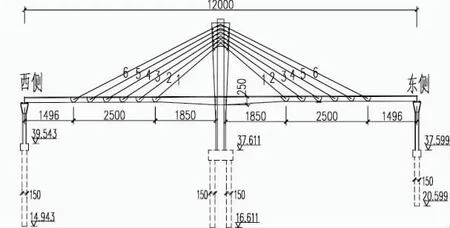
图1 基准桥桥型立面图

图2 有限元模型
主梁由弹性梁单元模拟,两跨总共划分120个单元。主塔,中墩和边墩同样地采用空间梁单元。索采用线弹性单元模拟[5]。斜拉索选用近似桁架单元的柔性索单元模拟,斜拉索利用虚拟刚臂与主梁相接。根据仙港大桥的地质资料[6],采用弹性梁单元模拟桩基础[7],每个桩单元高1m,并对每个单元设置横向和纵向的弹簧约束来模拟土弹簧。
3 参数选取及计算结果分析
桥梁的自振频率反映了桥梁的整体刚度,是桥梁进行动力分析时必须考虑的因素之一。本文通过搜集国内外已有的独塔部分斜拉桥的资料,详细归纳部分斜拉桥各个主要参数,在合理的范围内调整基准桥各个参数值,对独塔部分斜拉桥的动力特性响应进行分析研究。经过归纳筛选,最终选择了斜拉索间距、无索区长度、斜拉索布置形式、主塔高跨比、主梁高跨比、墩高和两跨跨径比等七个参数进行参数分析。
想要正确分析部分斜拉桥的空间动力特性,首先要弄清哪些振型是对部分斜拉桥动力响应影响最大的主振型。对常规斜拉桥的动力特性来说,最关注的振型是一阶对称竖向弯曲振型、反对称飘浮振型和一阶对称扭转为主振型。其中,反对称飘浮振型对车辆振动反应来说是基本的振型;一阶对称竖向弯曲振型、反对称飘浮振型对地震反应分析最为重要;一阶对称扭转、一阶对称竖向弯曲振型为主振型是主要用于风振分析[8]。对于连续梁桥来说其主要的振型则是主梁一阶竖向弯曲振型与一阶侧向弯曲。而对性能介于两者之间的部分斜拉桥,其又有自身的特点。部分斜拉桥相对影响较大的振型是主梁一阶竖向弯曲振型、一阶主梁侧向弯曲振型及主梁扭转振型,与斜拉桥相似,一般部分斜拉桥的主梁扭转振型与侧向弯曲振型耦联在一起。为了准确地分析结构参数对动力特性的影响,本文对基准桥梁的主要振型进行编号,对应的振型编号见表1。

表1 振型编序
3.1 斜拉索间距参数计算比较分析
斜拉索间距是指斜拉索在主梁上相邻锚固点之间的水平距离。部分斜拉桥的主梁截面高度较斜拉桥高,刚度较大,考虑到桥梁的施工与整体受力,部分斜拉桥的索距一般取3~5m[9],本文基准桥斜拉索索距为5m。文献[10]分别取2m、4m和12m对索距参数进行静力分析。文献[11]分别取索距为2m、4m、6m和12m建立模型进行动力方面的分析。本文选取索距2.5m,5m(基准桥),12.5m进行比较。索距参数的变化拟通过根数变化来实现,布索区域不变,塔上索距保持不变,同时保证斜拉索总截面面积不变,其他参数均保持不变。对模型进行编号,由索距从小到大依次为模型A、模型B(基准桥)、模型C。
图3绘出几个主要振型随着斜拉索距变化,其所处模态的频率的变化情况。
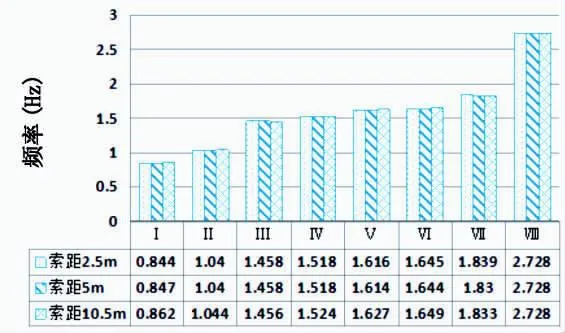
图3 索距动力特性比较
由图表可看出,随着索距离加大,除了主梁一阶对称竖弯和反对称竖弯有微小的变化外,其他主要振型几乎不变,可以得出结论,斜拉索距的变化对桥梁结构动力特性影响微小。
3.2 塔旁无索区长度参数计算比较分析
部分斜拉桥,塔底梁端由于截面刚度相对斜拉桥大,更趋向于连续梁桥,要承受较大的弯矩,导致支撑要求较大的刚性,为了整座桥梁体系受力较平顺,且为了让索尽可能的起到优化结构的作用,在塔根一定范围内会有一段无索区,以保证弹性支撑的有效性与连续性。无索区一般为跨度的1/3[12],这样对结构受力比较有利,本文无索区长度为20m,为跨度60m的1/3。文献[10]取塔旁无索区长度22m、25m、28m、31m和34m进行静力分析研究。文献[11]取塔盘无索区长度20m、25m、30m建立动力计算模型进行分析。塔端无索区大概是跨径的1/4~2/5,因此本文选取无索区分别为15m,20m(基准桥),25m进行比较。通过移动整个索区来满足无索参数的变化,其他参数均保持不变。对模型进行编号,由无索区从小到大依次为模型A、模型B(基准桥)、模型C。
图4绘出几个主要振型随着塔旁无索区的变化,其频率的变化情况。
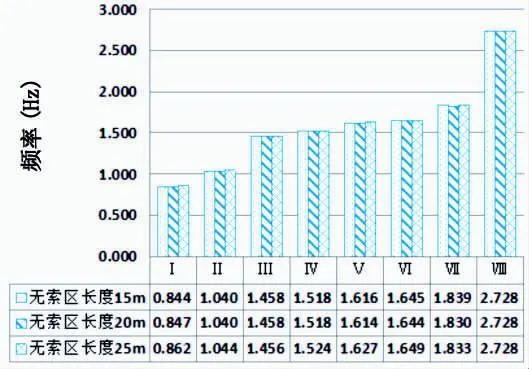
图4 塔旁无索区动力特性比较
由图表可看出,随着无索区加大,除了主梁一阶对称竖弯和反对称竖弯有微微变小外,其他主要振型几乎没变,且关于主梁振型的变化也很小,可以得出结论,塔旁无索区的变化对结构动力特性影响很小,故考虑动力响应时可以忽略其影响。该结论与文献[8]所得到的结论基本一致。
3.3 布索形式参数计算比较分析
索面的布置对桥梁的抗扭刚度有很大影响,故使用双索面的形式可以很大提高桥梁的抗扭能力,同时也对改善结构的抗风性的提高。文献[11]采用单索面和双索面作为参数变化参数分析了双塔部分斜拉桥的动力特性分析,本文同样也对独塔部分斜拉桥的索面形式进行分析。本文选取单索面和双索面(基准桥)作参数分析比较,为了不让桥塔和的刚度影响到参数分析的精度,通过移动并合并两塔索来满足索面形式的变化,其他参数均保持不变。对模型进行编号,由无索区从小到大依次为模型A、模型B(基准桥)。
图5绘出几个主要振型随着塔旁无索区的变化,及频率的变化情况。
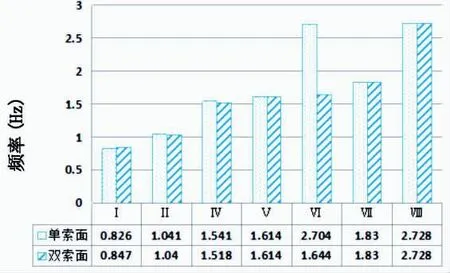
图5 布索形式动力特性比较
由图表能看出,两种布索形式对于独塔部分斜拉桥扭转振型和主梁侧弯振型的影响微小;对主塔横向振型的影响比较明显,基本影响不到其他部位的动力性能。结果显示部分斜拉桥主梁的刚度相对较大,斜拉索起到的作用仅仅是加劲作用。
3.4 主塔高跨比参数计算比较分析
相比常规斜拉桥,部分斜拉桥最显著的特征之一就是其塔高偏低。部分斜拉桥索对梁不再是竖向力为主,相反其轴向力的作用较为显著,因此部分斜拉桥的拉索可认为是主梁预应力体外索,当然其竖向力也起到一定的弹性支撑作用,减小了主梁跨中弯矩和梁根负弯矩,使梁的截面高度得以减小。部分斜拉桥的主塔约为常规斜拉桥的三分之一至二分之一。文献[12]对三塔部分斜桥进行塔高增加2m、4m和6m的静力分析;文献[13]也对部分斜拉桥的塔高参数进行静力特性分析,得到的结论基本相同。以上三篇文献对塔高的参数分析都是基于静力方面的分析,文献[11]分析了漳州战备大桥随塔高变化的动力特性,分别分析了主塔高跨比为1/12,1/10,1/8,1/6的塔高参数模型。国内外已建独塔部分斜拉桥的塔高与中跨跨度之比大部分在1/2.5~1/6之间,因此本文选取主塔高别为10,15m,22m(基准桥),25m进行比较。改变塔高的同时,其他参数均保持不变。对模型进行编号,由主塔高度从小到大依次为模型A、模型B、模型C(基准桥)、模型D。
图6绘出几个主要振型随着塔高的增大,其频率的变化情况。

图6 主塔高跨比动力特性比较
由图表可看出,塔高对于独塔部分斜拉桥主梁各个振型频率都有一定影响,随着塔高参数的变化,除了关于塔的振型变化较大外,其余各振型的变化不明显。从整体上看,塔高的变化对整桥的影响还是多方面的,不容忽视。文献[11]中塔高的变化,对桥梁动力特性的影响也相对较明显,由于其分析的结构型式与本文的独塔型式存在差异,因此该参数对各个振型的影响程度友各自的特点。
3.5 主梁高跨比参数计算比较分析
由于索的弹性支撑,以及索的体外预应力的作用,使部分斜拉桥桥的梁高相对连续梁桥大大减小,但相比常规斜拉桥,其主梁刚度又要大很多,实际受力中,主梁还是起主导作用。文献[12][13]都分别对部分斜拉桥的主梁高跨比进行静力分析,分析结果都认为主梁高跨比对桥梁的动力特性影响较大。文献[11]通过调整主梁刚度,研究分析了双塔部分斜拉桥的动力特性。主梁刚度的变化对性能跟趋近于连续梁体系的部分斜拉桥的影响是显而易见的,因此加入主梁跨高比参数分析对独塔部分斜拉桥的动力特性分析是很重要的。国内外已建独塔部分斜拉桥支点处主梁高跨大致在1/25~1/15之间,等截面区主梁高跨比大致在1/40~1/30之间。本文改变参数原则:在不改变变截面区段长度的前提下,按表2改变梁高,变截面区段截面变化同基准桥相同采用抛物线变化,桥梁其他参数均保持不变。
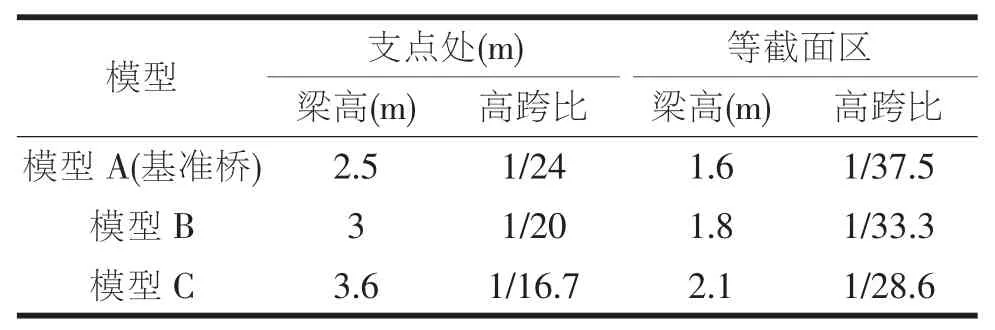
表2 主梁高度参数情况
图7绘出几个主要振型随着塔高的增大,其频率的变化情况。

图7 主梁高跨比动力特性比较
由图表可看出,主梁高跨比对独特部分斜拉桥的影响,主要反映在主梁自身的振型上,对其它振型的影响不是很明显。主梁高跨比的变化对全桥的刚度影响还是相当大的,因此,独塔部分斜拉桥动力分析中,主梁高跨比的确定,应充分考虑其影响。
3.6 墩高参数计算比较分析
由于部分斜拉桥的受力性能更接近于连续梁桥体系,且独塔部分斜拉桥主几乎都是塔梁墩固结,除去起加劲作用的索后,相当于T构桥,因此其墩高对部分斜拉桥的桥梁的动力特性影响应该是不容忽视的。针对部分斜拉桥的静力参数分析和动力分析相关的文献,都无对墩高参数的变化的分析,本文加入墩高参数进行分析。桥梁墩高因工程本身状况和地形而异,因此本文选取该墩高参数的选择不必参照国内外独塔斜拉桥的采用范围,同时对参数的选择不宜过大也不宜过小,过大不合实际,过小效果不明显,经过计算选择,本文选择在基准桥的基础上,中墩、边墩高度减少5m和增大5m来满足参数的变化。改变墩高的同时,其他参数保持不变。对模型进行编号,模型A(墩高减少5m)、模型B(基准桥)、模型C(墩高增大5m)。
图8绘出几个主要振型随着墩高的增大,其频率的变化情况。振型编号对应的振型类型见表3。
由图表可看出,独塔部分斜拉桥的墩高的变化对各个构件的振型影响都很大,唯独对主梁和主塔的对称振型影响很小。实际上墩高参数的影响效果,与对连续梁桥的影响是相同的,对独塔部分斜拉桥的影响是不容忽视的,故本文加入墩高参数进行分析。结果显示,墩高对全桥刚度的影响很大,同样对各个构件的影响也很明显。

图8 墩高动力特性比较
3.7 两跨跨径比参数计算比较分析
国内外独塔部分斜拉桥大多数采用对称布置,两跨不等的情况也不少,主要考虑地形因素、施工的可行性以及桥型的布置需要,而采用不等跨步对称布置。多塔部分斜拉桥的边主跨不对称,类似于多塔常规斜拉桥,不仅要考虑全桥的刚度、地形和施工的需求,还包括减小中跨跨中挠度和提高全桥整体刚度。由于部分斜拉桥受力性能相对更接近连续梁桥,故边主跨比的取值一般为0.6左右。对于独塔部分斜拉桥的两跨跨径比并没有严格的要求,由于主梁的刚度较大,允许两跨跨径比一定量的差别,若两跨跨径比过大,还可以用辅助墩来满足受力上的要求。文献[10][11]分别对三跨部分斜拉桥的边主跨进行静力参数分析和动力参数分析,得到的结果边主跨比对主梁无论是静力性能有较大的影响,而对动力特性的影响不是很大,更多的集中于主塔墩的影响。而独塔部分斜拉桥的两跨跨径比又与以上两者的情况又有所不同,本节以国内外独塔斜拉桥的两跨跨径比数据为依据,进行两跨跨径比对其动力特性影响的参数分析。国内外已建独塔部分斜拉桥两跨跨径比大致在0.6~1之间,因此本节选取四个参数进行分析,两跨跨径比分别为0.7(A)、0.8(B)、0.9(C)、1(D基准桥),参数改变通过改变边墩处无索区段长度来实现,桥梁其他参数均保持不变。
图9绘出几个主要振型随着两跨跨径比增大,其频率的变化情况。振型编号对应的振型类型见表1。
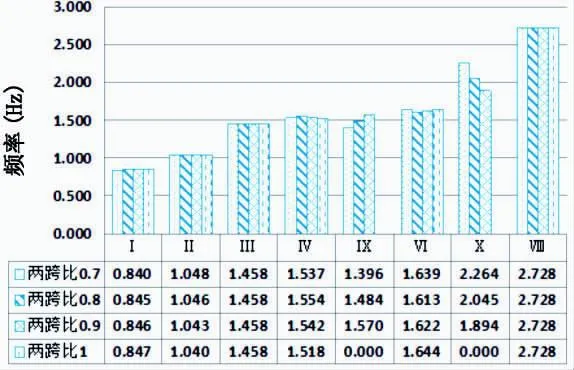
图9 两跨跨径比动力特性比较
由图表可看出,独塔部分斜拉桥的两跨跨径比的变化主要影响主梁面内竖弯,使两跨主梁振型出现顺序不一致,且随着跨度的变小,频率呈明显递减趋势。两跨跨径比的变化对其它振型的影响较小,对主塔横桥向不对称振型造成微小的影响,对其它部分则几乎不造成影响。独塔部分斜拉桥与多塔部分斜拉桥不同,其两跨跨径比的选用更多的是为了实际地形与结构的需要,因此考虑其两跨跨径比参数的影响,更多的是为不等跨的独塔部分斜拉桥做参考,选取最合适的两跨跨径比。
4 结论
4.1 参数敏感分析结论
由于部分斜拉桥的主塔和斜拉索只是辅助受力和加劲作用,其刚度主要由主梁提供,使得塔和索对其动力特性的影响是很有限的。而主梁刚度、塔高以及墩高参数的影响明显较大。本文通过7个设计参数的动力敏感性分析,得到以下几点关于独塔部分斜拉桥结构动力特性的分析结论:
(1)随着索距加大,除了主梁一阶对称竖弯和反对称竖弯有微小影响外,对其他主要振型影响小,几乎可以忽略。斜拉无索区的变化同样影响微小可忽略。布索形式总体来看不会影响到整座桥梁结构的动力性能,同时基本影响不到结构其他部位的动力性能。相关文献显示,斜拉索距、无所区长度和布索形式对整桥静力的影响相对较大[9],因此在做部分斜拉桥塔旁无索区长度的选取时可只考虑结构静力特性。
(2)主塔高度变化对主梁的影响很小。主塔高跨比的变化对主塔横桥向振型和纵桥向振型的影响都较大,随着主塔的塔高变大,在一定范围内其振型频率会趋于一个稳定的数值。随着主塔高跨比的增大,塔高对桥梁整体的影响效果趋向于常规斜拉桥的。
(3)主梁高跨比增大,全桥纵向振动随之变大,耦合主梁一阶反对称扭转、主梁一阶反对称侧弯振型频率略有增大。而主梁高跨比对塔振型的影响也仅仅通过索在纵向有微小的影响,对塔的横桥向振动基本没有影响。总之主梁高跨比的变化对以主梁刚度为主导的部分斜拉桥的动力特性影响是显而易见的。
(4)墩高的增大,全桥纵向和横向振动频率出现明显变小。独塔部分斜拉桥的墩高的变化对各个构件的振型影响都很大,唯独对主梁和主塔的对称振型影响很小。同连续梁桥体系相同,墩高对全桥刚度的影响很大,同样对各个构件的影响也很明显。
(5)由于主梁不对称布置,两跨主梁竖弯的振型也出现不一致,同时造成两跨主梁振型出现顺序不一致。基准桥模型的对称出现对称与反对称竖弯振型频率介于不对称模型的左右跨一阶竖弯的频率之间。两跨跨径比对主塔的振型影响较小。
4.2 独塔部分斜拉桥动力特点
与相应的常规斜拉桥、连续梁桥(刚构桥)相比,独塔部分斜拉桥具有如下的动力特点:
(1)相比动力特性受塔和索影响较大的常规斜拉桥[14],独塔部分斜拉桥所受的影响则小的多,从前四个参数分析结果可以看出索参数的变化造成的影响几乎可以忽略,而塔参数变化也仅仅使塔的振型产生较大变化,其次对面内竖弯振型的影响也是微小的。
(2)相比常规斜拉桥,独塔部分斜拉桥明显属于中短周期桥型,基本周期只有1~2s左右,而常规斜拉桥的基本周期基本都大于5s。常规斜拉桥的一阶振型多是纵飘或侧弯,而部分斜桥的一阶振型却是面内竖弯。独塔部分斜拉桥的扭转振型与侧弯振型强烈地耦合在一起,而没有出现纯扭转或纯侧弯的振型,这一特点与常规斜拉桥是相似的。由此可见扭转振型与侧弯振型耦联的依据是梁索塔的共同作用,也就是参入了索和塔因素而造成的响应结果。
(3)相比连续梁桥,独塔部分斜拉桥的面内竖弯振型出现较早,且频率值也小。与连续梁桥相似,主梁侧弯振型出现的较早,这点与独塔部分斜拉桥自身的整体结构刚度有关。从前十阶振型的分布来看,独塔部分斜拉桥与连续梁桥更为接近,因此独塔部分斜拉桥动力特性相对常规斜拉桥来看更接近与连续梁桥。
[1]王勖成,邵敏.有限单元法基本原理和数值方法.北京:清华大学出版社,2004.
[2]John CWilson,Wayne Gravelle.Modelling of a cable-stayed bridge for dynamic analysis.Earthquake Eng.Struct.Dyn.,1991,20:707-721.
[3]Kanok-Nukulchai W,Yiu P K,Broton D M.Mathematical modeling of cable-stayed bridges.IABSE Publications Committee,1992,2:108-113.
[4]Mand,J.B.,and Basoz,N.(1999).Seismic fragility curve theory for highway bridges.Proceedings of the 5th U.S.Conference on Lifeline Earthquake Engineering.Reston,Virginia:31-40.
[5]范立础.桥梁抗震.上海:同济大学出版社,1997.
[6]深圳市政设计院.仙港大桥工程勘察报告,0721001,2007.
[7]李捷,杨智.桥梁动力分析中桩基础的模拟.青海交通科技,2006,2:18-20.
[8]李国豪.桥梁结构稳定与振动(修定版).北京:中国铁道出版社,2003:388-396.
[9]欧阳永金.独塔单索面部分斜拉桥力学性能及建设实践.北京:中国铁道出版社,2006.
[10]申明文.部分斜拉桥静力分析:[硕士学位论文].上海:同济大学,2002.
[11]蔡鹏程.三跨预应力混凝土部分斜拉桥动力特性及地震反应特性研究:[硕士学位论文].福州:福州大学,2005.
[12]陈虎成,石雪飞.部分斜拉桥结构性能研究.结构工程师.2004,3:27-31.
[13]刘风奎,蔺鹏臻,孙红红.矮塔斜拉桥塔高优化.铁道工程学报, 2003,4:71-74.
[14]蔺鹏臻,刘风奎.拉索对斜拉桥体系面内弯曲频率的影响分析.城市道桥与防洪,2005,2:41-43.
