Fe3O4单晶薄膜磁性电场调控的微磁学仿真研究∗
2017-08-07杨芝张悦周倩倩王玉华
杨芝 张悦 周倩倩 王玉华
1)(武汉科技大学城市学院,武汉 430083)
2)(华中科技大学光学与电子信息学院,武汉 430074)
3)(武汉科技大学,冶金工业过程系统科学湖北省重点实验室,武汉 430081)
Fe3O4单晶薄膜磁性电场调控的微磁学仿真研究∗
杨芝1)张悦2)周倩倩2)王玉华3)†
1)(武汉科技大学城市学院,武汉 430083)
2)(华中科技大学光学与电子信息学院,武汉 430074)
3)(武汉科技大学,冶金工业过程系统科学湖北省重点实验室,武汉 430081)
(2017年3月9日收到;2017年4月24日收到修改稿)
磁性薄膜磁学特性电场调控的相关研究对开发新型低功耗磁信息器件具有突出意义.本文基于电场调控磁性的基本理论,以OOMM F(Ob ject Oriented M icro-M agnetic Frame)微磁学仿真软件为工具,研究了电场对生长于PZN-PT单晶衬底上Fe3O4单晶薄膜磁学特性的调控.研究结果显示:无外加电场时,薄膜表现出典型的软磁特性;沿衬底[001]方向施加的外加电场可以使得薄膜矫顽力、矩形比等磁学特性发生显著改变:当外加磁场沿[100]([010])时,施加正值(负值)电场强度可以显著增大薄膜的矫顽力与矩形比,当电场强度不小于0.6 MV/m时薄膜矩形比达到1.这是因为外加电场导致薄膜产生单轴应力各向异性,使得薄膜的等效磁各向异性发生了从无外电场下的面内四重磁晶各向异性向高电场下的近似单轴磁各向异性的过渡.外加1 MV/m与-1 MV/m的电场时等效易磁化轴分别沿[100]与[010]方向.另外,外加1 MV/m(-1 MV/m)的电场强度可以使得铁磁共振的频率增大(减小)接近1 GHz.
Fe3O4单晶薄膜,微磁学仿真,磁性,电场调控
1 引 言
用电场代替电流产生的磁场去调控磁性材料与器件的磁化状态具有非常重要的应用价值.比如,目前数据量的存储需求越来越大而存储器件尺度越来越小,这导致为写一个字节而通过电流产生的局部磁场会影响到近邻存储单元.利用电场调控材料磁性则有望减小所需的写入电流,因而对开发具有小尺寸、低功耗等突出优点的新型磁存储器件具有非常显著的应用潜力[1-3].
目前电场对磁性调控的相关研究已经包含电场调控的射频/微波器件[4-6]、电场调控磁阻器件[7-12]、电场调控的自旋转移矩-磁随机存储器(STT-MRAM)[13]、电场调控畴壁的动力学特性[14]、电场调控反铁磁绝缘体的反铁磁共振特性[15]、电场调控垂直磁化薄膜的垂直磁各向异性[16-18]等.特别是近期通过第一性原理计算及微磁学计算发现,外加电场有望极大地降低STT翻转磁矩所需的电流[19],甚至可能通过控制脉冲宽度实现磁矩在纯脉冲电场作用下的180°翻转,这对开发低功耗的新型磁存储器件而言意义重大[20].在上述研究中,电场调控磁性的基本物理机制主要包括界面电荷机制及应力机制两种.界面电荷机制是通过外加电场改变超薄磁性薄膜与电学材料界面电荷电子结构来改变磁性材料的磁各向异性等磁学特性.而应力机制则是通过对某些具有压电效应的铁电相(如PMN-PT,PZN-PT,PZT等)施加电场使其产生应变,该应变传递至具有磁致伸缩效应的磁性层使之产生应力,从而影响其磁各向异性等磁学特性.
相比界面电荷机制,基于应力机制的电场调控通常在样品制备上更简单些.到目前为止,各国研究人员已通过实验手段研究了各种磁性薄膜材料的各种磁学特性基于应力机制的电场调控[21],例如铁磁金属薄膜的磁各向异性和阻尼系数[22]、单晶磁性薄膜的磁性[23,24]、垂直磁化薄膜的矫顽力[25,26]、复合磁性薄膜的交换偏置效应[27,28]、铁磁薄膜的铁磁共振特性[4,5,29,30]、金属磁性薄膜的各向异性磁电阻效应[7]、金属多层薄膜的巨磁电阻(GMR)效应[8,10]、磁性隧道结的隧道磁电阻(TMR)效应[9]等.除上述实验研究,也有研究人员基于压电效应本构方程通过理论分析研究了电场对磁性材料磁学行为的调控,例如尖晶石型铁氧体薄膜磁性的电场调控[23].
实验研究无疑可以得到最接近实用的研究结果,然而针对复合材料的实验通常也存在很多可能会对实验结果产生影响的难以精确控制的复杂因素,比如样品制备的工艺控制和测试方法,这些因素通常容易使得实验结果难以重复.理论研究可以避免实验的这些非本征因素的干扰,从而使得研究结果更接近本征的物理行为.然而,针对具有复杂磁学电学特性的异质结构材料(如具有磁晶各向异性的单晶铁磁薄膜材料)的理论分析往往难以避免非常复杂的多元函数的数学计算,因而通常只能进行一些简化和近似处理.
除了上述实验和理论研究外,仿真计算也是研究材料磁学电学特性的一种有效方法.通过仿真通常可以在理论指导下给出非常接近本征规律的结果而避免繁杂的人工数学计算.Ob ject Oriented M icro-Magnetic Frame(OOMMF)是一种常用的磁学仿真开源软件,可下载于网站http://math. nist.gov/oomm f/contrib/oxsext/.然而,目前针对压电/单晶铁磁薄膜之类具有复杂磁学电学特性的异质结构材料磁性的电场调控的报道还未受到广泛关注.
2 仿真模型与原理
模拟仿真的物理模型如图1所示.对于压电层,我们采用PZN-PT单晶衬底;对于铁磁层,我们选取的材料为 Fe3O4软磁单晶薄膜,其尺寸为100 nm(长)×100 nm(宽)×10 nm(厚度).所加电场沿垂直膜面方向(z轴),大小从-1 MV/m变化至1MV/m.在压电衬底上施加电场会分别使在x轴和y轴方向上产生压缩和拉伸的应力,而磁场方向是沿面内[100],[010]方向.

图1 (网刊彩色)电场对铁氧体单晶薄膜的磁性的调控仿真模型示意图Fig.1. (color on line)Schem atic of the sim u lation model of electric-field control of m agnetic p roperties of a ferrite single-crystal fi lm.
磁性薄膜的自由能主要有磁晶各向异性能、塞曼能、退磁场能、应力能和交换作用能.而对于单层铁磁薄膜,仿真中采用周期性边界条件,忽略边界特性,因而不会产生涡旋磁矩及其导致的额外交换作用能.分别用(1),(3),(4)式表示磁晶各向异性能、退磁场能以及应力能.对于较大尺寸的纳米厚度薄膜而言,可以认为是一个无限大的平面,因而可以用(3)式近似表示其退磁能.当磁场沿着[100]方向时,塞曼能的表达式如(2a)式所示;当磁场沿着[010]方向时,塞曼能表达式如(2b)式所示.

式中的K1,K2分别为立方晶体的磁晶各向异性常数;µ0为真空磁导率;MS为饱和磁化强度;H为外加磁场大小;λ[100]表示在[100]方向的磁致伸缩系数(对于立方晶体,[010]方向的相关系数与之相同);θ为磁矩与z轴的夹角;φ为磁矩在xy平面的投影与 x轴的夹角. 对于Fe3O4单晶,K1=-9000 J/m3,K2=0 J/m3, MS=5.6×105A/m,λ[100]=-19 ppm[31].σc与σt分别表示在x轴和y轴的应力,可以表示为[32]

其中E为电场强度,Y为杨氏模量,ν为泊松比,对于Fe3O4,Y=230 GPa,ν=0.3[31];d31与d32为PZN-PT单晶衬底沿[100]与[010]方向的压电电压系数,分别为-3000 pC/N与1000 pC/N[32].结合(1)-(6)式可以得出 Fe3O4单晶薄膜在外加电场与磁场下的总自由能密度:

上式已经略去与角度无关的常数项,因为它们对磁矩最终稳定状态没有影响.
基于总自由能密度(7a)与(7b)式,我们还可以得出电场对Fe3O4单晶薄膜铁磁共振特性的影响.铁磁共振频率公式为
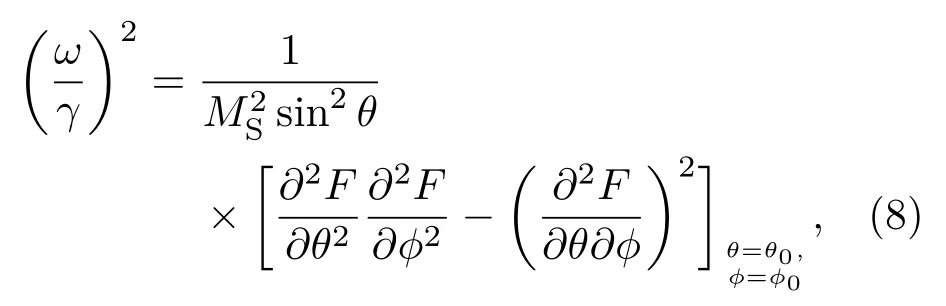
其中ω为铁磁共振频率,γ为电子旋磁比,θ0与φ0为稳定状态下的磁矩角度.
通过二元函数求极值可以最终确定其稳定状态.然而,人工计算量明显较大,不仅因为存在两个变量,而且存在着三角函数的高次项.也可以在上述理论分析的基础上求解Landau-Lifshitz-Gilbert (LLG)磁化动力学方程得到同样的结果.人为求解LLG方程非常繁复,然而该方程的数值求解可以通过OOMMF这种专门的微磁学计算软件实现.我们用OOMMF软件模拟仿真出不同电场的磁滞回线,从而反映出电场对铁氧体单晶薄膜的调控作用.使用OOMMF软件进行微磁学计算的核心机理是求解Gilbert形式的LLG动力学方程:

其中m为表示磁矩取向的单位矢量,是时空坐标的函数;t为时间;α为阻尼因子;Heff是有效磁场,可以表示为

其中µ0为真空磁导率,MS为饱和磁化强度,F为系统的总自由能密度.
利用OOMMF进行仿真计算首先需要对研究对象进行离散化处理,使得研究对象由微磁学格子所组成.每个格子的尺度不大于体系的交换长度.具体而言,对于Bloch型畴壁,对应的交换长度为

其中A与K分别为交换常数和磁各向异性常数.而对于软磁薄膜材料,更多时候其交换长度通过下式计算:

根据Fe3O4的磁学参数(K与MS如上所述,A= 10-11J/m). 我们根据(11)式计算得到lex= 33 nm,而根据(12)式计算得到lex=7 nm.因此,我们进行仿真所采用的微磁学格子单元在x,y, z三个方向的尺寸分别为5,5,1 nm.
在上述几何离散化基础上,进一步要对体系自由能离散化.对于某一个格子i,利用OOMMF计算可以考虑的自由能包括:交换能,磁各向异性能,塞曼能,退磁能.
格子i的交换能密度(Eex)i可以表示为:

上式中Aij为格点i与最近邻的格点j之间的交换常数,mi与mj分别为格点i与格点j磁矩取向单位矢量,Δij为格点i与格点j之间的距离.求和遍及最近邻的所有格点.
对于立方单晶材料,其格点i的磁晶各向异性能密度(Ek)i可以表示为

其中(K1)i与(K2)i分别为第i个格点的磁晶各向异性常数,θ与φ的定义如图1所示.对于具有单轴各向异性磁性材料,其格点i的磁各向异性能密度(Ea)i表示为

其中Ki为第i个格子的单轴磁各向异性常数.
在均匀磁场作用下第i个格点磁矩的塞曼能密度为

其中H为外加磁场的磁场强度.
第i个格点离散形式的退磁能密度为

其中(Hd)i为第i个格点的局域退磁场.考虑每个格子尺度小于交换长度,内部磁矩规则排列,故而只用考虑表面磁荷对退磁场的贡献.因此,(Hd)i可以表示为

其中ri与rj代表第i与第j个格子中心的空间坐标;n为第j个格子表面法向单位矢量;积分范围为第j个格子的表面.使用OOMMF软件计算退磁场利用的是快速Fourier变换法[33].
格点i的总自由能密度:

将(13)-(19)式代入(11)式可以计算得到格点i的等效场,进而代入(9)式通过数值求解LLG方程可以确定格点i磁矩的动力学行为.所有格点磁矩动力学行为的集合就得到整个体系的磁化动力学行为.
在我们的仿真研究中,在给定Fe3O4薄膜外形尺寸、单元格子尺寸以及各磁性参数(外加电场导致的应力各向异性等效为一单轴各向异性)的基础上,我们进而在x,y方向尝试施加不同的磁场直到达到稳定(单位磁矩取向随时间的变化率d m/d t<0.01)的磁化强度略微小于饱和磁化强度(单位磁矩取向在x或y轴投影(mx或my)大于0.95).而后以此为初始态,设置磁场从此正向饱和磁场逐步变化到负向饱和磁场再返回正向饱和磁场,形成一个完整的循环.磁场施加间隔为5 m T,每个磁场下收敛条件均为d m/d t<0.01.即在某磁场下,当磁化强度满足条件d m/d t<0.01时,磁场自动改变5 m T,并以前一磁场下得到的稳定的磁化强度为初始进行计算,最终得到一个完整的磁滞回线.
3 结果与讨论
3.1 PZT-PT/Fe3O 4系统外电场作用下磁滞回线的OOM M F仿真结果
我们通过OOMMF软件对Fe3O4/PZN-PT系统在不同电场强度下的磁滞回线进行模拟仿真,电场的大小从-1 MV/m变化至1 MV/m.图2(a)与图2(b)分别表示沿着x轴和y轴施加磁场后,在不同电场强度下Fe3O4/PZN-PT系统的磁滞回线.

图2 (网刊彩色).不同电场作用下Fe3O4/PZN-PT系统的归一化磁滞回线 (a)沿x轴施加磁场;(b)沿y轴施加磁场Fig.2.(color online)Electric-field dependence of the norm alized m agnetic hysteresis loops of Fe3O4/PZN-PT system m easured with them agnetic field app lied along(a)x axis and(b)y axis.
从图2中我们可以看到:当电场为1 MV/m,沿 x轴施加磁场所得磁滞回线形状类似于矩形,矩形比达到1,此时x轴为易磁化轴;当电场值从1 MV/m逐渐减小至-1 MV/m时,磁滞回线的形状逐渐变缓变窄,矩形比逐渐减小.当外电场减小到-0.6 MV/m及以下时,矩形比减小为零,说明沿着x轴磁化难度逐渐加强.当施加的电场为-1MV/m时,沿y轴施加磁场所得矩形比达到1,此时易磁轴为y轴;随着电场逐渐增大到0.6 MV/m及更大时,y轴变为难磁化轴.值得注意的是,这一结果与Sun课题组[29]报道的实验结果基本一致.从应用角度讲,这种高矩形比对磁信息存储的稳定性非常重要.

图3 不同电场下的磁滞回线的矩形比 (a)沿x轴施加磁场;(b)沿y轴施加磁场Fig.3.E lectric-field dependence of the squareness ratio of the norm alized m agnetic hysteresis loopsm easu red with them agnetic field app lied along(a)x axis and(b)y axis.
图3(a)和图3(b)分别表示沿着x轴和y轴施加磁场后,在不同电场强度下Fe3O4/PZN-PT系统的矩形比(MR/MS,MR为剩余磁化强度).从图3可以看出,当-0.5 MV/m<E<0.5 MV/m时,磁滞回线表现为有一定剩磁和矫顽力的曲线,表明x和y轴均非易磁化轴,易磁化轴的方向应当介于两者之间.
另外,我们注意到在选取的电场范围内,在任意磁场作用下,系统磁矩在z方向的分量都远小于其在x与y方向上的分量.这表明在所施加的电场范围内,薄膜的退磁能无法被其他各向异性能(包括磁晶各向异性能和应力各向异性能)克服.因而在稳定状态下磁矩处于xy面内,即θ0=90°.通过对(7a)与(7b)式进行代数计算也可以得到上述结果,但无疑非常大的计算量.
3.2 对仿真结果的分析
3.2.1 基于等效磁各向异性能的分析
我们可以通过外加电场对体系等效磁各向异性能的影响解释仿真结果.根据(1)-(6)式,考虑θ0=90°,可以得到外电场作用下的等效磁各向异性能密度为
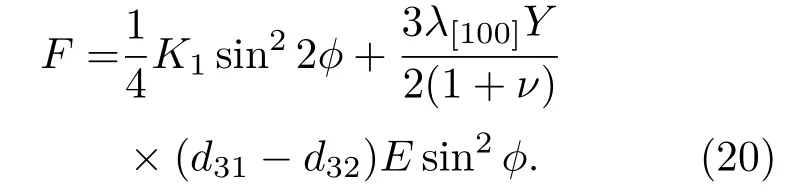
将相关参数代入表达式(20)后,可得到关于Fe3O4等效磁各向异性能表达式:

图4是不同电场下的F与φ的函数图像.

图4 (网刊彩色)不同电场值下F与φ的函数图像Fig.4.(color on line)E lectric-field dependence of F as a function ofφ.
从图4中可以看出,当不施加电场时,系统呈现出面内磁晶各向异性,易磁化方向对应的φ分别为45°,135°,225°,以及315°,即对应[110]与[1¯10]两个易磁化轴的方向.当电场为±1 MV/m,曲线接近普通正弦曲线形状,说明电场引起的单轴应力各向异性远强于Fe3O4的面内磁晶各向异性.当电场为1 MV/m,且φ为90°或270°时,等效磁各向异性能F最大;而当φ为0°或180°时,等效磁各向异性能F最小.因而当电场为1 MV/m时, x方向为易磁化轴,因而磁滞回线矩形比为1.而当电场为-1 MV/m时,在φ为90°或270°时,等效磁各向异性能F最小;而当 φ为0°或 180°时,等效磁各向异性能F最大,y方向为易磁化轴.因而,沿y轴方向(即φ为90°或270°)时磁滞回线矩形比为1.当电场强度为0.4,-0.4,0.2,-0.2 MV/m时,单轴的应力各向异性和单晶薄膜本征各向异性相差不大,对应的易磁化轴明显介于x轴和y轴之间.对于正值电场,随着其电场强度数值逐渐向1 MV/m增加,易磁化轴为[100]方向的单轴应力各向异性显著大于薄膜的本征各向异性,其易磁化轴从无外加磁场下的φ=45°逐渐移向x轴,对应沿x轴方向施加磁场所得矩形比逐渐增大.相反,对于施加负值电场,单轴应力各向异性的易磁化轴为[010],随着其电场强度数值逐渐向-1 MV/m,应力各向异性也显著大于薄膜的本征各向异性,易磁化轴从无外加磁场下的φ=45°逐渐移向y轴,对应沿y轴方向施加磁场所得矩形比逐渐增大.
3.2.2 外加电场作用下系统磁滞回线的解析表达式
根据稳定平衡态下θ0=90°,容易得到总自由能的表达式(22a)和(22b),

式中F[100]([010])分别代表外加磁场沿x(y)轴时的自由能密度.相比(7a)与(7b)式,上式已经简化为一元函数,因而进一步的代数运算也简化很多.
根据稳定平衡条件:

可以得到达到稳定平衡时


此即在特定电场下磁滞回线满足的方程.
3.2.3 外加电场对铁磁共振频率的影响
以外加磁场沿x轴方向为例,根据(8)式,并且考虑达到稳定平衡时θ0=90°,可以得到[30]

根据所有已知参数以及通过微磁学仿真得到的H-cosφ关系,可以最终计算得到不同电场强度下铁磁共振线频率f=ω/2π与外加磁场强度H的关系(如图5所示).
从图5(a)和图5(b)可以看出,外加正电场会导致在特定磁场下铁磁共振频率的增大,而外加负值电场则产生相反的效果,即导致铁磁共振频率的减小.如图5(c)所示,外加105m T磁场时,铁磁共振频率和外加电场的电场强度改变发生单调变化.相比无外加电场的情形,外加±1 MV/m的电场强度可以使得铁磁共振的频率发生接近1 GHz的变化.根据上述微磁学仿真结果,外加正电场会使得x方向变为易磁化轴,这等于在x方向产生了一个等效磁各向异性场,从而增大了铁磁共振频率.而外加负电场则会减弱x方向的各向异性场,从而减小其铁磁共振频率.

图5 (网刊彩色)(a)外加正电场下铁磁共振频率和外磁场的关系式;(b)外加负电场下铁磁共振频率和外磁场的关系式;(c)在105 m T磁场作用下,外加特定电场使得铁磁共振频率发生的偏移量Fig.5. (color on line)Ferrom agnetic resonant frequency as a function of external m agnetic field under(a)positive electric fields and(b)negative electric fields;(c)electric-field induced shift of ferrom agnetic resonant frequency under the m agnetic field of 105 m T.
4 总 结
我们结合磁学基本理论和微磁学仿真的方法研究了电场对PZN-PT单晶衬底上Fe3O4单晶薄膜磁性的调控.得到以下结果:
1)首先通过微磁学仿真,我们发现在所施加的电场范围内,Fe3O4单晶薄膜将保持其面内磁各向异性,在此基础上,我们可以将二元函数的自由能密度简化为一元函数,从而可以显著简化后续计算;
2)在1)的基础上,我们结合微磁学仿真和简化后的代数计算得到:
①当外加电场强度从0增加到1MV/m时,沿x方向施加磁场所得磁滞回线形状逐渐类似于矩形,随着电场逐渐增大到0.6 MV/m及更大时,y轴变为难磁化轴,并且沿x方向施加磁场所得铁磁共振频率也随外电场强度增大而提高,当x方向施加105 m T磁场时,外加1 MV/m电场可以使得铁磁共振频率相比无外加电场时提高接近1 GHz;这是因为在这个过程中沿着x轴磁化越来越容易,当电场强度不低于0.6 MV/m时,电场诱导的易磁化轴沿[100]的单轴应力各向异性能将远强于薄膜本征的磁晶各向异性能;
②当外加电场强度从0增加到-1 MV/m时,我们发现沿y方向施加磁场所得磁滞回线形状逐渐类似于矩形,随着电场逐渐增大到-0.6 MV/m及更大时,x轴变为难磁化轴,并且沿x方向施加磁场所得铁磁共振频率也随外电场强度增大而降低,当x方向施加105m T磁场时,外加-1 MV/m电场可以使得铁磁共振频率相比无外加电场时降低接近1 GHz;这是因为在这个过程中沿着y轴磁化越来越容易,当电场强度不低于-0.6 MV/m时,电场诱导的易磁化轴沿[010]的单轴应力各向异性能将远强于薄膜本征的磁晶各向异性能.
[1]Hu JM,M a J,Wang J,Li Z,Lin Y H,Nan C W 2011 J.Adv.D iel.1 1
[2]Dong S,Liu JM,Cheong SW,Ren Z F 2015 Adv.Phys. 64 519
[3]Hu J M,Chen L Q,Nan C W 2016 Adv.M ater.28 15
[4]Sun N X,Srinivasan G 2012 SPIN 2 1240004
[5]Liu M,Sun N X 2014 Phil.Trans.R.Soc.A 372 20120439
[6]Luo M,Zhou P H,Liu Y F,W ang X,X ie J L 2017 M ater.Lett.188 188
[7]Liu M,Li S,ObiO,Lou J,Rand S,Sun N X 2011 Appl. Phys.Lett.98 222509
[8]G iang D T H,Thuc V N,Duc N H 2012 J.M agn.M agn. M ater.324 2019
[9]Li P S,Chen A T,Li D L,Zhao Y G,Zhang S,Yang L F,Liu Y,Zhu M H,Zhang H Y,Han X F 2014 Adv. M ater.26 4320
[10]Lei N,Devolder T,Agnus G,Aubert P,Daniel L,K im J V,Zhao W S,Trypiniotis T,Cowburn R P,Chappert C,Ravelosona D,Lecoeur P 2013 Nat.Comm un.4 1378
[11]G rezes C,Ebrahim i F,Alzate J G,Cai X,Katine J A, Langer J,Ocker B,K halili Am iri P,W ang K L 2016 Appl.Phys.Lett.108 012403
[12]Yoshida C,Noshiro H,Yam azaki Y,Sugii T,Furuya A, A taka T,Tanaka T,Uehara Y 2016 A IP Adv.6 055816
[13]W ang K L,Alzate J G,K halili Am iri P 2013 J.Phys. D:Appl.Phys.46 074003
[14]Lin W,Vernier N,Agnus G,Garcia K,Ocker B,Zhao W,Fu llerton E E,Ravelosona D 2016 Nat.Comm un.7 13532
[15]Sekine A,Chiba T 2017 A IP Adv.7 055902
[16]Ib rahim F,Yang H X,Hallal A,D ieny B,Chshiev M 2016 Phys.Rev.B 93 014429
[17]Park K W,Park J Y,Baek S H C,K im D H,Seo S M,Chung SW,Park B G 2016 Appl.Phys.Lett.109 012405
[18]Liu Y,Hu F X,Zhang M,W ang J,Shen F R,Zuo W L,Zhang J,Sun J R,Shen B G 2017 Appl.Phys.Lett. 110 022401
[19]Zhang X,W ang C,Liu Y,Zhang Z,Jin Q Y,Duan C G 2016 Sci.Rep.6 18719
[20]Zhu W,X iao D,Liu Y,Gong S J,Duan C G 2014 Sci. Rep.4 4117
[21]Yang C C,W ang F L,Zhang C,Zhou C,Jiang C J 2015 J.Phys.D:Appl.Phys.48 435001
[22]Taniyam a T 2015 J.Phys.Condens.M at.27 504001
[23]Hu J M,Nan C W 2009 Phys.Rev.B 80 224416
[24]Li N,Liu M,Zhou Z Y,Sun N X,M u rthy D V B,Srinivasan G,K lein T M,Petrov V M,Gup ta A 2011 Appl. Phys.Lett.99 192502
[25]Lei N,Park S,Lecoeur P,Ravelosona D,Chappert C, Stelm akhovych O,HolýV 2011 Phys.Rev.B 84 012404
[26]Liu M F,Hao L,Jin T L,Cao JW,Bai J M,W u D P, W ang Y,W ei F L 2015 Appl.Phys.Express 8 063006
[27]Lebedev G A,V iala B,Lafont T,Zakharov D I,Cugat O,Delam are J 2011 Appl.Phys.Lett.99 232502
[28]Rizwan S,Yu G Q,Zhang S,Zhao Y G,Han X F 2012 J.Appl.Phys.112 064120
[29]Liu M,Obi O,Cai Z H,Lou J,Yang G M,Ziem er K S, Sun N X 2010 J.App l.Phys.107 073916
[30]Zhou H M,Chen Q,Deng J H 2014 Chin.Phys.B 23 047502
[31]Zhang Y,Zhou Q Q,D ing J J,Yang Z,Zhu B P,Yang X F,Chen S,Ouyang J 2015 J.Appl.Phys.117 124105
[32]Liu M,Obi O,Lou J,Chen Y J,Cai Z H,Stoute S, Espanol M,Lew M,Situ X D,Ziem er K S,Harris V G, Sun N X 2009 Adv.Funct.M ater.19 1826
[33]Zhu J G,Neal Bertram H 1988 J.Appl.Phys.63 3248
(Received 9 March 2017;revised manuscript received 24 April 2017)
Electric-field control of magnetic properties of Fe3O4single-crystal film investigated by micro-magnetic simulation∗
Yang Zhi1)Zhang Yue2)Zhou Qian-Qian2)Wang Yu-Hua3)†
1)(City College,Wuhan University of Science and Technology,Wuhan 430083,China)
2)(School of Optical and Electronic Information,Huazhong University of Science and Technology,Wuhan 430074,China)
3)(Hubei Province Key Laboratory of Science in Metallurgical Process,Wuhan University of Science and Technology, Wuhan 430081,China)
Control of magnetic p roperties by an app lied electric field has significant potential app lications in the field of novel m agnetic in form ation devices,with som e advantages such as low dissipation and sm all sizes.T ill now,m any scientific and technical p roblem s in this field have been w idely investigated theoretically and experim entally.However,a lacuna stillexists in the papers concerning the investigations perform ed bymicrom agnetic simu lation which is a powerful tool for revealing magnetic behaviors in a com p licated magnetic system.Based on the basic princip le for electric-field m anipulation ofm agnetic p roperties,we study the electric-field control ofm agnetic properties of a square-shaped singlecrystal Fe3O4thin fi lm form ed on a single-crystal PZN-PT piezoelectric substrate by the microm agnetic simu lation method via ob ject oriented micro-m agnetic fram e(OOMMF),a software for microm agnetic simu lation.Them agnetic hysteresis loops are collected for the Fe3O4/PZN-PT com posite system under magnetic fields app lied in the[100]and [010]crystallographic directions of Fe3O4and an electric field app lied along the[001]axis of the PZN-PT substrate. The app lied electric field acts as an stress anisotropy energy.The result of our simulation is sim ilar to the reported resu lt of an experim ental investigation for the sam e system and is consistent with that of our theoretical analysis based on a therm odynam ic route.The resu lts reveal that the fi lm exhibits typical soft-m agnetic behavior without app lying an electric field.W hen an electric field is app lied to the PZN-PT substrate,the coercivity and squareness ratio of Fe3O4is greatly aff ected.Under an externalmagnetic field along the[100]axis of Fe3O4,the app lying of a positive electric field clearly enhances the coercivity and squareness ratio.On the other hand,when an externalm agnetic field is app lied along the[010]direction of Fe3O4,the coercivity and squareness ratio is increased by app lying a negative electric field.In both cases,the coercivity and squareness ratio reaches 1 when the absolute value of E is 0.6 MV/m or larger.This high coercivity and squareness ratio is vital tomagnetic in formation memory.These resu lts are attributed to the com petition between an electric-field-induced uni-axial stressanisotropy energy and the intrinsic in-p lane four-fold m agnetocrystalline anisotropy energy of a Fe3O4thin fi lm.W hen the absolute value of E is su ffi ciently large(1 MV/m), the electric-field-induced stress anisotropic energy signifi cantly overweighs the intrinsic m agnetocrystalline anisotropy energy,and the Fe3O4thin fi lm exhibits an approxim ate uniaxialm agnetic anisotropy energy.Under the electric fields of 1-MV/m and-1-MV/m,the effective easy axis is along the[100]and[010]direction of the Fe3O4thin fi lm,respectively. Additionally,we also find that app lying a 1-MV/m(-1-MV/m)electric-field can cause the frequency for ferromagnetic resonance to increase(reduce)alm ost 1 GHz,off ering the possibility of developing a microwave device with tunable frequency.
Fe3O4single-crystal fi lm,micromagnetic simulation,magnetic properties,electric-field control
PACS:75.78.Cd DO I:10.7498/aps.66.137501
∗武汉科技大学城市学院博士基金(批准号:2014CYBSKY 003)和国家自然科学基金(批准号:11574096)资助的课题.
†通信作者.E-m ail:wangyuhua@w ust.edu.cn
PACS:75.78.Cd DO I:10.7498/aps.66.137501
*Pro ject supported by the Ph.D.Program s Foundation of City College,W uhan University of Science and Technology,China (G rant No.2014CYBSKY 003),and the National Natu ral Science Foundation of China(G rant No.11574096).
†Corresponding au thor.E-m ail:wangyuhua@w ust.edu.cn
