逾渗分立时间量子行走的传输及纠缠特性∗
2017-08-07安志云李志坚
安志云 李志坚
(山西大学理论物理研究所,太原 030006)
逾渗分立时间量子行走的传输及纠缠特性∗
安志云 李志坚†
(山西大学理论物理研究所,太原 030006)
(2016年12月18日收到;2017年4月1日收到修改稿)
在一维分立时间量子行走中,通过静态和动态两种方式随机地断开连接边引入无序效应,研究了静态逾渗和动态逾渗对量子行走传输特性以及位置自由度和硬币自由之间纠缠的影响.随着演化时间的增加,静态逾渗会使得量子行走从弹道传输转变为安德森局域化,而动态逾渗则会使之转变为经典扩散.理想情况下,量子纠缠在较短的时间内就达到一个常数值E0.静态逾渗量子行走的纠缠减小,并随着时间做无规振荡,而动态逾渗量子行走的纠缠则会随着时间光滑地增加,并在某一时间超过理想情况下的常数值,表现出动态逾渗增强量子纠缠的特性.
逾渗量子行走,概率分布,量子纠缠
1 引 言
量子行走作为经典随机行走的量子力学推广,同样具有连续时间量子行走[1]和分立时间量子行走[2]两种形式来描述粒子在分立格点上的相干动力学行为.连续时间量子行走遵从分立空间的薛定谔方程,其在位置空间的哈密顿量由描述粒子在相邻格点之间跃迁的转移矩阵给出.分立时间量子行走则直接通过幺正算符重复作用于系统的初态来定义,除了位置空间之外,还需要一个硬币空间,由硬币态决定它在位置空间中移动的方向,幺正演化算符的生成元可等效为相对论狄拉克粒子的哈密顿量[3].由于量子行走在不同路径上传播的相干叠加和干涉效应,使得它与经典随机行走相比表现出多种不同的动力学行为[4,5].比如,一个典型的不同之处就是量子行走的位置方差随着时间平方增加,表现出量子弹道传输行为,而经典随机行走的位置方差随着时间线性增加,做经典扩散传输.这样,量子行走具有比经典随机行走更快的传播速度,而且人们基于这一特性为量子计算设计了更有效的量子搜索算法[6,7].鉴于经典随机行走在不同领域的广泛应用和量子行走的优越性,近些年人们在理论和实验上对量子行走进行了大量的研究.实验上,人们已经利用核磁共振[8]、囚禁离子[9]、光格子中的冷原子[10]以及波导阵列[11]等不同的物理系统实现了量子行走,为模拟复杂物理系统的量子动力学提供了广阔平台.理论上,量子行走除了用来设计量子算法之外,还被用来解释像光合作用中能量传输这样的复杂问题[12]、论证原子的相干操控[13]以及探索拓扑相[14]等.无序效应[15]、缺陷[16]、粒子间的相互作用[17],以及初态统计特性[18]等对量子行走的影响也受到了人们的广泛关注,由此探讨量子行走从弹道传输向经典扩散和局域化的过渡.
除了传输特性之外,量子行走另一个可应用的重要特征是位置自由度和硬币自由度之间的纠缠[19-21].量子纠缠是量子信息处理中的重要物理资源,它可以是一个大系统中不同子系统之间的纠缠,也可以是一个系统中不同自由度之间的纠缠.量子纠缠是量子系统特有的性质,经典物理中与之没有对应.噪声、量子测量或周围环境等的影响一般都会导致纠缠的减小或完全消失,解决这一问题的一种方法就是生成纠缠,量子行走就是生成纠缠的一个过程.由于纠缠会对理解许多物理现象,如超辐射、无序效应以及经典转变等给出新的洞察,因此研究量子行走纠缠对于开拓量子行走的实际应用具有重要意义.对于时间和空间都均匀的量子行走,两种自由度之间的纠缠大小一般情况下一开始会有所涨落,但随着演化步数的增加,涨落越来越小,最终会趋于某一渐近值,而且这一渐近值的大小依赖于量子行走的初态和硬币算符的选取.目前,时间和空间非均匀量子行走的纠缠引起了人们的极大关注,不同的无序效应会对纠缠的产生带来不同的影响[22-24].
分立时间量子行走是通过条件平移算符和硬币算符相继作用于当前状态来完成一步演化的,其中只有硬币参数而没有势能的概念,空间无序可以通过位置依赖的随机硬币参数来引入,以此等效位置势[25].同理,如果硬币参数随机地依赖于量子行走的步数,则构成时间上的无序.基于此,人们通过对分立时间量子行走的位置态或硬币态的周期测量、应用随时间或位置变化的硬币算符等方式,对量子行走的去相干、无序效应以及散射特性进行了大量研究[26-31].去相干和无序效应会使得量子行走的传输特性发生变化,一般情况下导致两种结果:一种是随着时间的增加,会使得方差随时间的二次增长行为最终被抑制,转变为随时间正比增长的经典扩散行为;另一种是长程干涉消失,只在初始位置附近发生多条传播路径相应传播幅度的干涉行为,最终表现为安德森局域化.最近,文献[22,23]研究了与时间和空间相关的随机硬币对分立时间量子行走产生纠缠的影响,指出使用与时间有关的动态随机硬币算符会使得量子行走产生最大纠缠.本文中,我们并非在分立时间量子行走的硬币空间引入无序,而是类似于连续时间行走,通过随机地断开相邻格点间的连接边在位置空间中引入无序,形成逾渗系统.我们首先给出模型,介绍无序的引入,定义静态和动态逾渗分立时间行走;接着通过数值计算分别研究逾渗效应对量子行走传输特性和产生纠缠的影响;最后给出结论.
2 逾渗分立时间量子行走
假设有一个由N个格点组成的一维系统,这样就会有N-1条相邻格点的连接边,如图1(a)所示.我们赋予每条边一个取值范围为0到1的随机数,如相邻两格点x和x+1的连接边的随机数记为Rx,一条边是否断开由与之对应的随机数决定.给定一个临界值p0,如果Rx≤p0,则表示格点x和x+1之间的连接边是相连的,否则,则表示两格点之间是断开的.这样就形成了一个逾渗系统.在计算过程中,如果进行多次计算取平均,那么随机取得每一个随机数的概率是相同的,这样p0就是整个系统连接边连通的概率,称为逾渗概率.如果p0=1,则一维格点链中的每条边都是连通的;反之,p0=0则表示一维格点链中的每条边都是断开的.
量子行走的希尔伯特空间是位置空间和硬币空间的直积空间,即,其中位置空间HP由格点对应的态矢量|x〉(x∈Z)张开;硬币空间HC由表硬币正反面的态矢量|c〉=|↑〉,|↓〉张开.在量子系统中,粒子的内禀自由度(如自旋)可以用来实现硬币空间,此时量子态不仅为正交的正反面态,而且可以是它们的任意叠加态.这样,量子行走的基矢为,其任意态可表示为
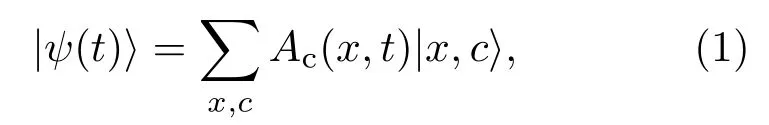
其中Ac(x,t)为t时刻量子行走硬币态为c且位于x处的概率幅.量子行走的一步演化由硬币算符C和依赖于硬币态的条件平移算符S对其量子态的相继作用得到,即

其中IP是作用在位置空间的单位算符.本文中,我们选取矩阵元都为实数的Hadam ard算符为硬币算符,即
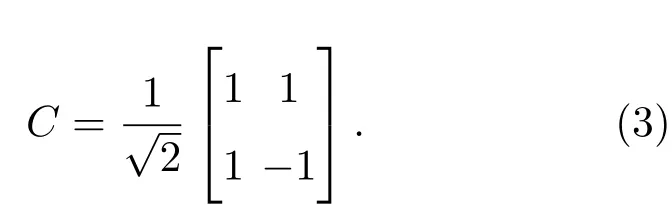
考虑逾渗后,条件平移算符可表示为


图1 条件平移示意图 (a)与x格点相连的两条边都连通;(b)与x格点相连的两条边中的一条断开;(c)与x格点相连的两条边都断开;弧形实线箭头表示硬币向上的粒子向右行走一步,弧形虚线箭头表示硬币向下的粒子向左行走一步,圆形箭头表示粒子不动但相应的硬币态翻转Fig.1.Sketch of conditional shift:(a)Both links connected to x site are connected;(b)one link connected to x site is b roken;(c)both links connected to x site are broken.The solid curved arrow denotes the particle with up coin state walking to right neighbor site while the dashed cu rved arrow denotes the particle with down coin statewalking to left neighbor site,and the circled arrow m eans the particle does notm ove but its coin state reverses.
若把所有连接边对应的随机数分布叫做“逾渗分布”,则根据逾渗分布在时间上的不同,我们可将系统分为两种逾渗类型.如果量子行走在每一步中所选的逾渗分布是相同的,也就是说每一步行走的条件平移算符相同,这样的逾渗系统称静态逾渗系统;如果量子行走在每一步中都重新选择一个逾渗分布,也就是说每一步行走的条件平移算符不同,则称这样的逾渗系统为动态逾渗系统.对于静态逾渗系统,量子行走演化t步后的波函数为|ψ(t)〉=Ut|ψ(0)〉;而对于动态逾渗系统,t步后的波函数为.
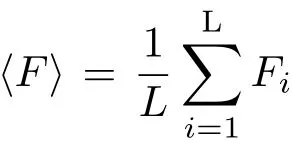
3 逾渗量子行走的传输特性
对于一个在分立时间和分立空间上都保持平移不变的量子行走,位置方差随时间平方变化的弹道传输行为是其一个标志性特征,这是时间演化过程中不同行走路径之间发生量子相干的直接结果.然而这种相干性非常脆弱,很容易遭到破坏.本部分中,我们主要考虑分立时间行走中连接边随机连通的逾渗过程,研究静态逾渗和动态逾渗以及逾渗概率对量子行走传输特性的影响.
把方程(1),(3)和(4)代入方程(2),则与硬币态相关的概率幅可表示为

从(5)式可以看出,如果所有连接边都连通,量子行走每演化一步就会新增两个格点被粒子占据,所以如果粒子初始时刻位于0格点处,那么行走t步后最多在0格点周围2t+1个格点上的分布概率不为零;而且对于Hadamard硬币算符,远离初始位置波前的传播速度为,因此这种量子行走在位置空间的传播范围为.如果有的连接边断开,则量子行走就会在相应格点处停止向前传播,我们考虑连接边断开的随机性,对不同的结果进行多次的统计平均,这样原则上量子行走不会在某格点处停止不前,仍然会扩展至的格点范围,但由于量子相干性的减弱或破坏,会导致经典扩散或安德森局域化.下面我们给出一维无限长格点上逾渗量子行走概率分布的统计平均
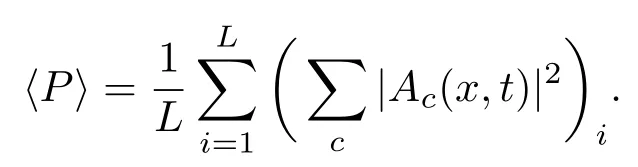
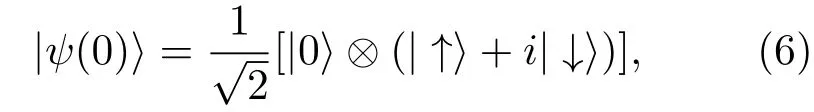
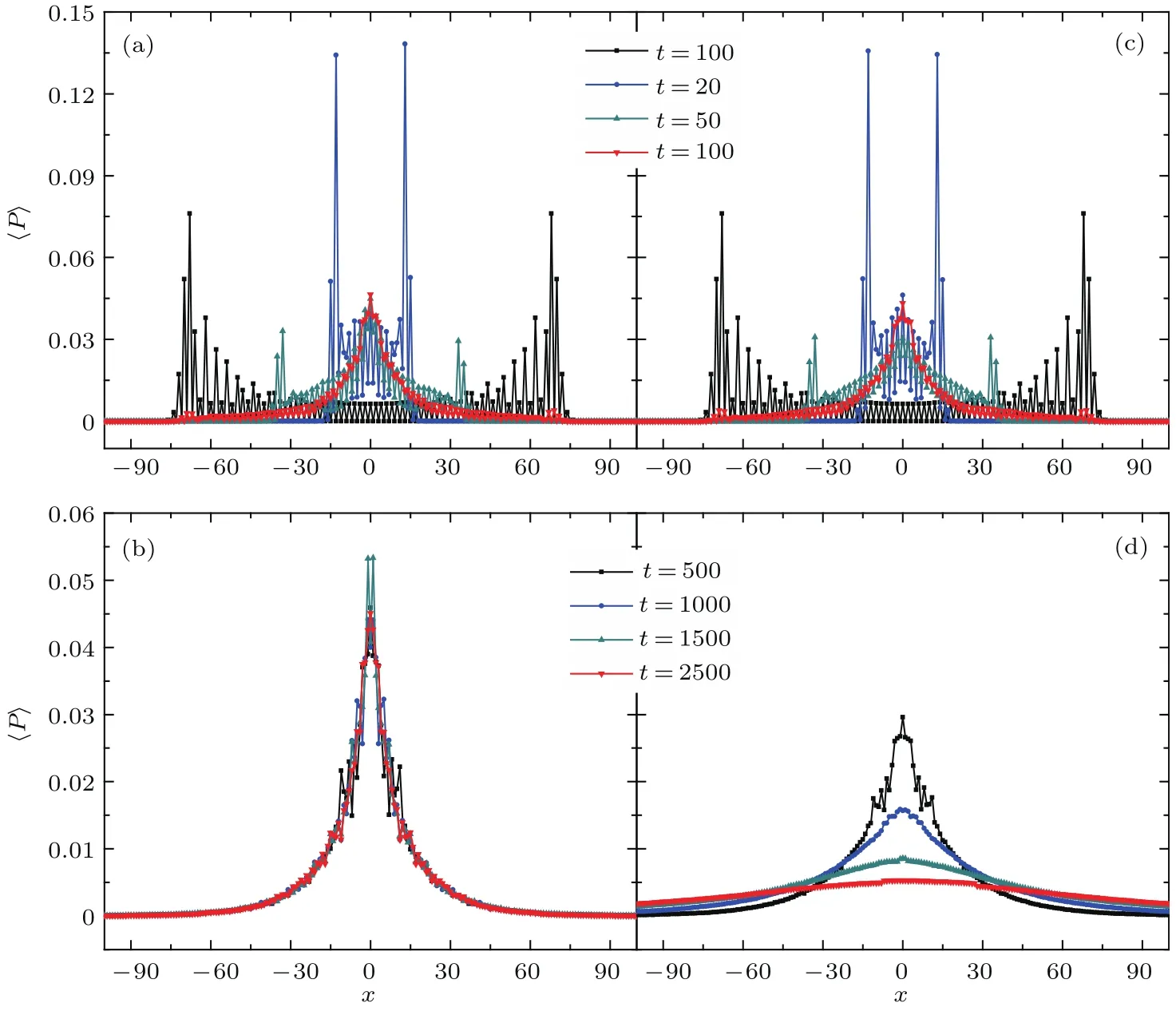
图2 (网刊彩色)逾渗概率p0=0.95,在不同演化步数下逾渗量子行走的概率分布 (a),(b)为静态逾渗情况; (c),(d)为动态逾渗情况;为了比较,其中(a)和(c)中的黑实线为无逾渗时的概率分布Fig.2.(color on line)W hen percolation p robability p0=0.95,the average p robability d istribu tions of percolation quantum walk are p lotted for d iff erent time steps:(a),(b)A re the static percolation cases;(c), (d)are the dynam ical percolation cases.For com parison,the solid b lack curves in Figs.(a)and(c)are the p robability d istribution without percolation.
这样的初态选取可以导致理想(无逾渗)量子行走在均匀一维格点上关于初始位置对称的概率分布,如图2(a)和图2(c)中的黑色曲线所示.图2中其他曲线给出p0=0.95时不同演化步数下逾渗量子行走的概率分布,图2(a)和图2(b)对应静态逾渗量子行走,图2(c)和图2(d)对应动态逾渗量子行走.众所周知,理想量子行走演化偶数(奇数)步时,其在奇数(偶数)格点位置上的分布概率为零,而且分布概率主要集中在远离初始位置的波前位置.当加入逾渗后,量子行走的每一步演化,都会使得传播范围内的所有格点上都具有占有概率,破坏了理想时只在奇或偶格点上分布的特点.当演化步数较少时,图2(a)和图2(c)表明,无论是静态逾渗还是动态逾渗,量子行走在远离初始位置的波前处有较大分布概率的相干性特征可以保持,但随着演化步数的增加,波前处的分布概率会越来越小,而初始位置附近的分布概率却越来越大,而且这种变化过程动态逾渗量子行走要比静态逾渗量子行走更快一些.随着演化步数的进一步增加,图2(b)和图2(d)显示出静态逾渗量子行走和动态逾渗量子行走表现出两种不同的极限分布.在长时间演化下,静态逾渗使得量子行走在不同路径间的长程干涉效应消失,但在初始位置附近仍然有一定的概率发生多条传播路径之间的短程干涉,这样,量子行走的概率分布范围不再随着时间发生变化,被局域在初始位置附近,表现出明显的安德森局域化特征;而动态逾渗不仅会使得长程干涉消失,而且也会使短程干涉消失,量子相干性被彻底破坏,动态逾渗量子行走虽然也是在初始位置附近分布概率最大,但随着时间的增加,其峰的高度越来越低,包络的宽度越来越宽,表现出典型的经典高斯波包扩散行为.由此可见,静态逾渗和动态逾渗对量子行走的影响有着本质不同的区别,前者导致了安德森局域化,而后者导致了经典扩散传输.
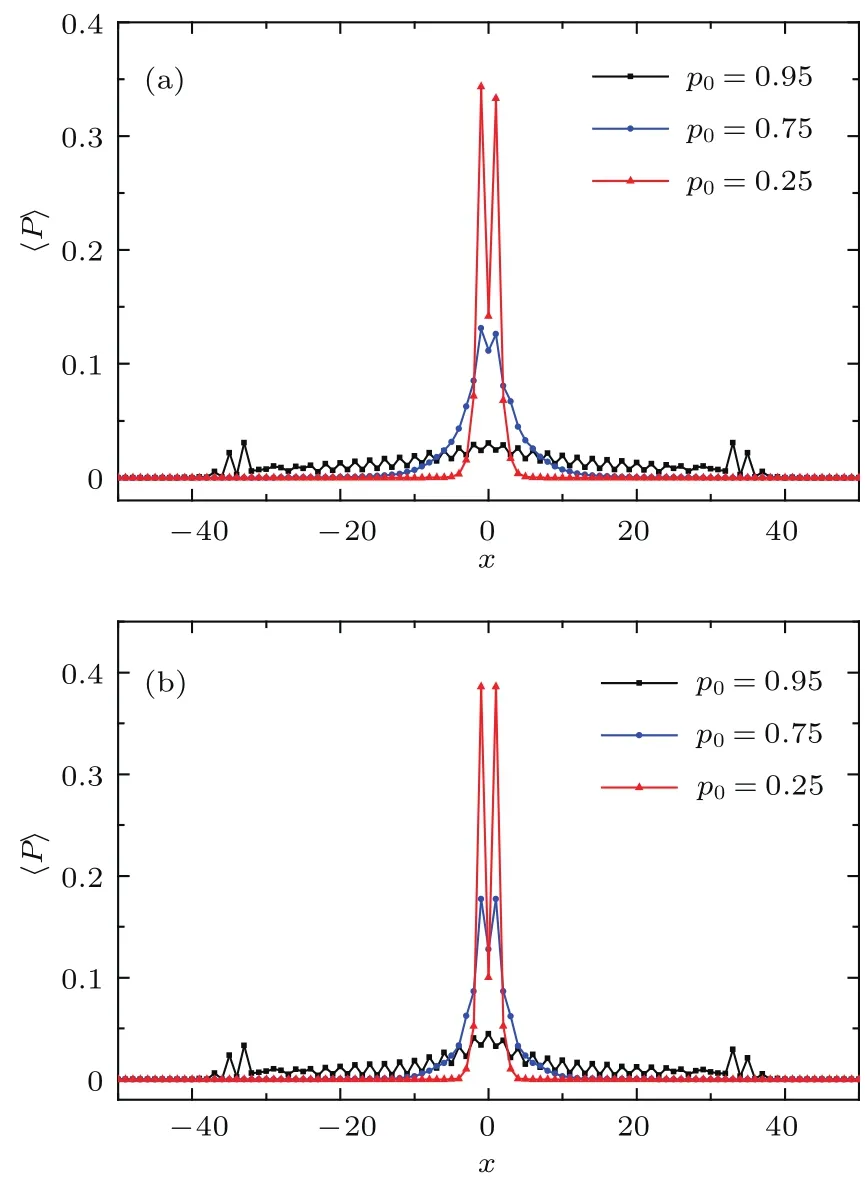
图3 (网刊彩色)演化步数t=50,选取不同逾渗概率时的量子行走的概率分布 (a)静态逾渗;(b)动态逾渗Fig.3.(color on line)W hen time steps t=50,the average p robability d istributions of percolation quantum walk are p lotted for d iff erent percolation p robabilities: (a)Is the static percolation case;(b)is the dynam ical percolation case.
在量子行走从相干弹道传输到经典扩散传输或安德森局域化的转变过程中,除了如图2所示与演化步数的长短有关外,也与逾渗概率的大小有关.总的来说应该与已传播范围内的连接边连通的数目有关.在图3(a)和图3(b)中,我们分别给出t=50步时静态逾渗量子行走和动态逾渗量子行走在不同逾渗概率p0下的概率分布,随着逾渗概率的减少,也就是连接边断开的增多,发生转变的过程更快,相应的局域化强度更强或经典扩散更慢.
4 逾渗量子行走的纠缠动力学
目前有关量子纠缠的度量有很多种不同的方式,如冯·诺依曼熵、共生纠缠度、量子失协等.在本文的研究中,我们总是选取纯态为分立时间量子行走的初态,再加上即使考虑连接边的随机断开过程,整个系统的时间演化仍然是幺正的,所以整个系统会一直保持为纯态.这样,我们可以选择冯·诺依曼熵来衡量量子行走位置自由度和硬币自由度之间的纠缠.冯·诺依曼熵由位置空间或硬币空间的约化密度算符态来定义,而且二者定义的结果完全一致[32].若t时刻整个系统的密度算符为ρ(t)=|ψ(t)〉〈ψ(t)|,对硬币自由度或位置自由度求迹,可获得位置空间或硬币空间的约化密度算符分别为

这样两种自由度之间的纠缠(冯·诺依曼熵)定义为
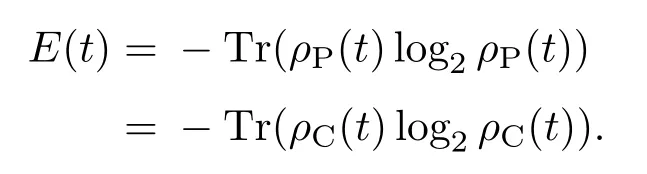
我们选取硬币空间约化密度算符ρC(t)来计算纠缠,一般地,ρC(t)在硬币空间{|c〉}中可表示为矩阵形式
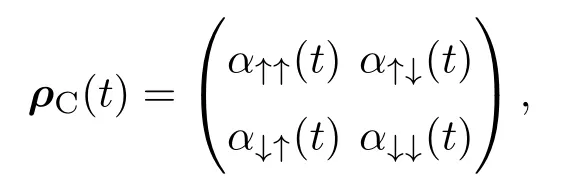
其中矩阵元αc,c,(t)与方程(1)中的系数Ac(x,t)之间具有关系,

和

如果二维矩阵ρC(t)的本征值为λ1(t)和λ2(t),则纠缠熵可进一步表示为
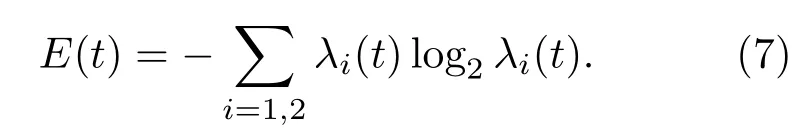
其取值范围为E(t)∈ [0,1],对于最大纠缠态E(t)=1,而对于可分离态E(t)=0.计算过程中,若λi=0,虽然log2λi会发散,但仍然取λilog2λi=0.
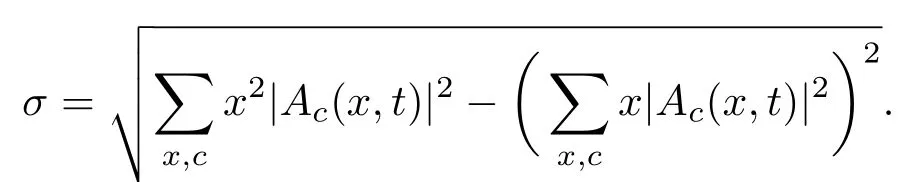
标准偏差越小,主峰结构越高越窄,相应的聚束效应越强.图5给出了逾渗量子行走的统计标准偏差随时间的变化,不同曲线对应不同的逾渗概率取值.图5(a)显示静态逾渗量子行走的位置标准偏差在p0较大时随着时间的增加可近似为一不变的常数值,p0较小时也是在某一常数值附近振荡,这也说明概率分布的峰的宽度不再随时间发生变化,表现为局域化效应.而对于动态逾渗量子行走,图5(b)则显示位置标准偏差随着时间以的形式增加(或在这一递增曲线附近振荡增加),说明概率分布的峰宽随时间逐渐增加,聚束效应减弱,表现为经典扩散行为.对于p0=1的全连通情况,量子行走的位置标准偏差随时间t线性增加,是典型的弹道传输特征,此时由于概率分布有两个主峰(如图2所示),不能再用标准偏差来描述概率分布的聚束效应.对比图4和图5,发现对于静态或动态逾渗量子行走,逾渗概率越小,局域化越强或经典扩散越慢,相应聚束效应较强,因此纠缠值越小.对比静态逾渗、动态逾渗和无逾渗三种情况,其中具有局域化效应的静态逾渗量子行走的聚束效应最强,其纠缠值也越小;无逾渗量子行走虽然在位置空间的传输范围最大,但其分布概率主要集中在展开边缘的两个小区域内,其聚束效应要强于经典扩散的动态逾渗量子行走,因此其纠缠小于动态逾渗时的纠缠.
图4 (网刊彩色)选取不同的逾渗概率,量子行走硬币自由度和位置自由度之间的纠缠随演化步数的变化 (a)静态逾渗;(b)动态逾渗Fig.4.(color on line)The variations of entanglem ent with time steps are p lotted for different values of percolation probability:(a)Static percolation;(b)dynam ical percolation.
图5 (网刊彩色)选取不同的逾渗概率,量子行走的位置标准偏差随演化步数的变化 (a)静态逾渗;(b)动态逾渗Fig.5.(color online)The variations of standard deviation with time steps are p lotted for d iff erent values of percolation p robability:(a)Static percolation;(b)dynam ical percolation.
5 结 论
在一维分立时间量子行走中,我们通过连接边的随机连通或断开引入无序效应,并针对量子行走的传输和纠缠特性研究了这种无序效应所产生的影响.无序效应的引入有两种不同的形式:一种是静态逾渗,也就是量子行走在每一步中连接边连通或断开的分布是相同的;另一种是动态逾渗,就是在量子行走的每一步中都重新选择新的连接分布.本文采用Hadamard硬币算符,且假定初始时刻量子行走处于x=0的中心格点位置和理想情况下能导致概率对称分布的硬币态.经过多次计算的统计平均结果表明,随着演化时间的增加,静态逾渗量子行走和动态逾渗量子行走的传播特征会由量子相干的弹道传输分别向安德森局域化和经典扩散行为转变.两种转变的快慢都依赖于逾渗概率的大小,逾渗概率越小,转变得越快.与不同的传输特性对应,量子行走中的位置自由度和硬币自由度之间的纠缠也表现出不同的动力学变化行为.理想情况下,量子纠缠在较短的时间内就达到一个常数值E0(∼0.85).静态逾渗会使得纠缠减小,并随着时间增加做无规律振荡,而动态逾渗量子行走的纠缠则会随着时间光滑地增加,并在某一时间超过理想情况下的常数值,表现出动态逾渗增强量子纠缠的特性.随着逾渗概率的减小,静态逾渗和动态逾渗都会使得纠缠减小,但在无穷长时间极限下动态逾渗量子行走的纠缠会趋向最大纠缠值且与逾渗概率的大小无关.在量子行走中,演化过程中的干涉效应起着非常重要的作用.我们的研究结果表明,静态逾渗和动态逾渗模型的幺正量子操作可以为量子信息处理和量子态的储存提供有效方法,无序和纠缠的关系有助于通过人造平台探索和理解自然界中的无序过程.
[1]Farhi E,Gutm ann S 1998 Phys.Rev.A 58 915
[2]Aharonov Y,Davidovich L,Zagury N 1993 Phys.Rev. A 48 1687
[3]Chand rashekar C M 2013 Sci.Rep.3 2829
[4]K em pe J 2003 Con tem p.Phys.44 307
[5]Zabu rdaev V,Denisov S,K lafter J 2015 Rev.M od.Phys. 87 483
[6]Am bainis A 2003 In t.J.Quan tum Inf.1 507518
[7]Childs A M,Gosset D,W ebb Z 2013 Science 339 791
[8]Du J,Li H,Xu X,Shi M,W u J,Zhou X,Han R 2003 Phys.Rev.A 67 042316
[9]Schm itz H,M atjeschk R,Schneider Ch,G lueckert J,Enderlein M,Huber T,Schaetz T 2009 Phys.Rev.Lett.103 090504
[10]K arski M,Forster L,Choi J M,Steff en A,Alt W, M eschede D,W idera A 2009 Science 325 174
[11]Xue P,Qin H,Tang B,Zhan X,Bian Z H,Li J 2014 Chin.Phys.B 23 110307
[12]Engel G S,Calhoun T R,Read E L 2007 Nature 446 782
[13]Chand rashekar C M 2011 Phys.Rev.A 83 022320
[14]K itagawa T,Rudner M S,Berg E 2010 Phys.Rev.A 82 033429
[15]BeggiA,Buscem i F,Bordone P 2016Quan tum Inf.Process.15 3711
[16]Li Z J,W ang J B 2015 Sci.Rep.5 13585
[17]W ang L,W ang L,Zhang Y 2014 Phys.Rev.A 90 063618
[18]W ang Q H,Li Z J 2016 Ann.Phys.373 1
[19]D i Franco C,M c Gettrick M,Busch T 2011 Phys.Rev. Lett.106 080502
[20]Goyal S K,Chand rashekar C M 2010 J.Phys.A:M ath. Theor.43 235303
[21]Carneiro I,Loo M,Xu X 2005 New J.Phys.7 156
[22]V ieira R,Am orim E P M,Rigolin G 2014 Phys.Rev.A 89 042307
[23]V ieira R,Am orim E P M,Rigolin G 2013 Phys.Rev. Lett.111 180503
[24]Chand rashekar C M 2012 arX iv:12125984v1
[25]Li Z J,Izaac J A,W ang J B 2013 Phys.Rev.A 87 012314
[26]Y in Y,K atsanos D E,Evangelou S N 2008 Phys.Rev. A 77 022302
[27]Schreiber A,Cassem iro K N,Potocek V,Gab ris A,Jex I,Silberhorn C 2011 Phys.Rev.Lett.106 180403
[28]TörmäP,Jex I,Sch leich W P 2002 Phys.Rev.A 65 052110
[29]Chou C I,Ho C L 2014 Chin.Phys.B 23 110302
[30]W ang D D,Li Z J 2016 Acta Phys.Sin.65 060301(in Chinese)[王丹丹,李志坚2016物理学报65 060301]
[31]Lam H T,Szeto K Y 2015 Phys.Rev.A 92 012323
[32]Bennett C H,Bernstein H J,Popescu S 1996 Phys.Rev. A 53 2046
(Received 18 Decem ber 2016;revised manuscript received 1 April 2017)
Properties of distribution and entanglement in discrete-time quantum walk with percolation∗
An Zhi-Yun Li Zhi-Jian†
(Institu te of Theoretical Physics,Shanxi University,Taiyuan 030006,China)
We investigate one-dimensionaldiscrete-time quantum walk on the linewhere the linksbetween neighboring sitesare random ly broken.Two link-broken ways,static percolation and dynam icalpercolation,are considered.The formerm eans that the broken links are fixed in position space at each time step,while the latter is that broken links are varied with time step.Our attention focuses on the effects of these disorders on two physical quantities,the probability distribution and the entanglem ent between the coin degree of freedom and position degree of freedom.Choosing Hadam ard coin operator and assum ing the walker to start from the position eigenstate|0〉and attach itself to a coherent coin state,we give the statistical average results after making numerical calculationsmany times.The choices of coin operator and initial state,resu lting in a symm etric p robability distribution about origin in the ideal case,is help ful in com paring with different cases in different disorder strengths.It is shown that the probability distribution of static percolation quantum walk can change from a coherent behavior at short time to Anderson localization at longer time,while the dynam ical percolation quantum walk can change to a classical diff usive behavior.W ith the decrease of the percolation probability,these transitions become faster.The entanglement for ideal case without disorder reaches a constant value after a short time evolution.The static percolation m akes the entanglem ent less than that of ideal case and fluctuate irregu larly around a certain value.The situation is very different for the dynam ical percolation: the entanglement increases smooth ly with the time step and can exceed the constant value in the ideal case at some time.Both of entanglem ents for two types of percolations decrease with reducing percolation probability.As a striking characteristic,the entanglem ent in dynam ical case can tend to m aximum regard less of percolation probability in long time lim it,while the static case cannot.In themodel for our study,the random ized unitary operations,induced by the static and dynam ical percolations,can lead to som e noticeable effects on the transport and entanglem ent of discrete time quantum walk.The results about the interplay between disorder and entanglem ent not only assist quantum inform ation processing,but also give more options to further explore and understand disorder physical processes in nature.
percolation quantum walk,probability distribution,quantum entanglement
PACS:03.67.Bg,05.40.FB,03.65.-w DO I:10.7498/aps.66.130303
∗山西省回国留学人员科研资助项目(批准号:2015-012)和山西省面上自然科学基金(批准号:201601D 011009)资助的课题.†通信作者.E-m ail:zjli@sxu.edu.cn
PACS:03.67.Bg,05.40.FB,03.65.-w DO I:10.7498/aps.66.130303
*Project supported by ShanxiScholarship Councilof China(Grant No.2015-012),and Natural Science Foundation of Shanxi Province,China(G rant No.201601D 011009).
†Corresponding author.E-m ail:zjli@sxu.edu.cn
