混沌光场光子统计分布及二阶相干度的分析与测量∗

兰豆豆1)2) 郭晓敏1)2) 彭春生1)2) 姬玉林1)2) 刘香莲1)2)李璞1)2) 郭龑强1)2)†

1)(太原理工大学,新型传感器与智能控制教育部重点实验室,太原 030024)

2)(太原理工大学物理与光电工程学院,光电工程研究所,太原 030024)

混沌光场光子统计分布及二阶相干度的分析与测量∗

兰豆豆1)2) 郭晓敏1)2) 彭春生1)2) 姬玉林1)2) 刘香莲1)2)李璞1)2) 郭龑强1)2)†

1)(太原理工大学,新型传感器与智能控制教育部重点实验室,太原 030024)

2)(太原理工大学物理与光电工程学院,光电工程研究所,太原 030024)

(2017年1月24日收到;2017年3月27日收到修改稿)

利用通信波段双通道单光子探测器,采用Hanbury Brown-Twiss关联测量方案,理论分析并实验测量了光反馈半导体激光器产生的混沌光场的光子统计分布及不同混沌状态光场的二阶相干度.通过对混沌光场二阶相干度g(2)(τ)的理论分析,得出随着延迟时间和相干时间的变化,其与相干光、热光及单光子态的二阶相干度可明显区分并呈现出不同分布.同时实验上产生了频谱宽度6.7 GHz的混沌光场,测量了不同光子数分布的结果,并用高斯随机分布、泊松分布、玻色-爱因斯坦分布对光子数分布进行理论拟合,发现随着入射平均光子数的增加,光子数分布从玻色-爱因斯坦分布过渡到泊松分布,但整个过程都与高斯随机分布符合较好,且光场的二阶相干度g(2)(0)由2降至1.通过改变偏置电流(I=1.0Ith−2.0Ith)和反馈强度(0—10%),实验上研究了混沌光场由低频起伏到相干塌陷的过程中不同状态宏观动力学特性与二阶相干度的对应关系.结果表明:混沌光场在此过程中始终呈现出明显的聚束效应,并在频谱宽度最大时达到最强;同时给出了光子计数测量中聚束效应减弱的物理原因.实验表明该系统及方法能很好地揭示不同状态混沌光场的光子统计特性.

混沌激光,二阶相干度,单光子计数,半导体激光器

1 引 言

探索光场的高阶相干性及量子统计特性已成为量子光学研究的重要内容之一[1],而对其的深刻认识可追溯到20世纪50年代Hanbury-Brown和Twiss(HBT)的不同时空点的强度关联测量[2]以及1963年Glauber提出的光场相干性理论[3,4].之后不久利用光电倍增技术,Arecchi等完成了相干光及热光场光子统计分布的测量[5],并在阈值附近获得上述光场的相干特性[6].与此同时,Morgan和Mandel[7]利用单探测器测得热光场的聚束效应.随后HBT关联测量被应用于揭示光场反聚束效应[8]及光子亚泊松分布[9]等非经典特性.随着光电探测技术的迅速发展,人们已经可以从单光子水平上对光场进行分析和测量.单光子探测技术作为最灵敏的光学探测手段以及它在量子光学和量子信息方面的重要作用[10],已被广泛应用于量子保密通信[11]及光场精密测量[12]等方面.至此结合单光子探测技术的HBT关联测量,可精确反映光场的光子统计特性及光源的动力学产生过程,利用HBT关联测量所得到的光场的二阶相干度g(2)(τ),不仅可以评估辐射场的强度关联起伏和量子特性,而且还可用来区分不同光场,如热光场零延时的二阶相干度g(2)(0)>1,光场呈现出明显的聚束效应[13];相干光的g(2)(0)=1,光子数分布呈现随机的Poissonian分布;而亚泊松分布的量子辐射光源g(2)(0)<1,辐射光场呈现出显著的反聚束效应[14].近期基于单光子计数的HBT关联测量已被广泛应用于光场空间相干特性的分析[15,16]、鬼成像[17,18]、不同轨道角动量组分和角位置的方位角HBT(azimuthal HBT)干涉效应[19]、单光子源辐射光场的统计特性分析[20,21]等方面.

混沌激光场由于其宽频谱、类噪声、对初值敏感、长期不可预测、复杂度大等方面的特性满足信息安全及密码学的基本要求,在当今信息科学技术高速发展的趋势下,已引起了人们的广泛关注且进行了深入的研究[22],并被应用到高速远程混沌保密通信[23,24]、快速物理随机数产生[25,26]、基于公共信道的混沌密钥分发[27]等诸多领域.在20世纪90年代,基于混沌同步和混沌控制的方法,美国的Roy小组[28]首次利用两个光纤激光器实现了混沌光通信.之后的十多年间,相关混沌光场的产生及应用方面得到迅速发展.2005年,欧洲七个国家共八个研究组织在商用的光通信网络中完成了基于半导体激光器传输距离120 km,速率1 Gb/s,误码率10−7的混沌保密通信[24].2008年,日本的Uchida小组[29]用宽带大幅度混沌激光实现了1.7 Gb/s的物理随机数实时输出,相继以色列的Kanter[30]以及我国西南大学吴正茂研究组[31]利用混沌激光在实验上产生了更高速率的物理随机数.之后在光通信高速发展的推动下,有关混沌激光保密通信的研究一直十分活跃[22].但相关混沌光场的研究主要集中在时域和频域等宏观动力学特性[32],而判别分析混沌光场的方法主要是通过观测时域强度起伏、频谱宽度,分析系统的李雅普诺夫指数(Lyapunov exponent)、分叉图等来确定分岔点、普适费根鲍姆常数(universal Feigenbaum constant)及周期性等多方面的信息,最终确定混沌状态并与噪声进行区分,但是并不能得到光场的高阶相干性及光子统计分布等方面的更多信息.针对混沌激光光场量子统计特性的研究还并不深入,目前物理参数的测量已经达到量子水平,人们正努力寻求克服量子涨落,实现亚量子噪声测量的新方法[12].相关方法初步被应用到量子点反馈混沌激光场[33]和纳米激光器自反馈产生的混沌光场的量子统计特性[34]的分析研究,但上述特定光源的结构相对复杂,成本较高,所产生的混沌频谱宽度有限.能否在典型的混沌带宽较宽、初始光场参数可控的条件下,利用HBT方案在单光子水平上测量分析混沌光场的光子统计分布及二阶相干度,并与其他光场进行区分,就成为本文研究的重点.

本文利用工作在通信波段的双通道单光子探测器,利用HBT关联测量方法,首先对光反馈半导体激光器产生的混沌光场二阶相干度及光子数分布进行了理论分析,同时判别分析了不同光场的二阶相干度.在此基础上实验测量了宽带混沌光场的光子数统计分布及其二阶相干度,随后测量了不同反馈强度和偏置电流条件下混沌光场的二阶相干度.研究表明,混沌光场由低频起伏(low freque-ncy fl uctuation,LFF)进入相干塌陷(coherence collapse,CC)过程中,光场呈明显的聚束效应.我们通过对不同状态下混沌光场的光子统计分布和二阶相干度的理论分析和实验测量,表明通过该方案可准确地得到混沌光场的量子统计特性,进一步可用于混沌光场微观随机性及噪声特性的测量.

2 理论分析

混沌光场的产生可被认为N个激发态原子或是偶极子独立自发地辐射光子,N个随机辐射方向电磁场的矢量叠加.而其时域瞬时起伏的本质主要决定于碰撞展宽的机制,辐射和多普勒展宽在此时可被忽略,同时碰撞所引起的弹性随机相位改变不会影响原子的能态.故其随机辐射电场为[1,34]

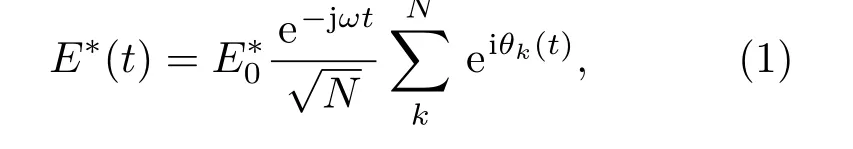
其中ω为载波频率,θk为随机相位.同时随机起伏的噪声频率˙θk满足如下关系:

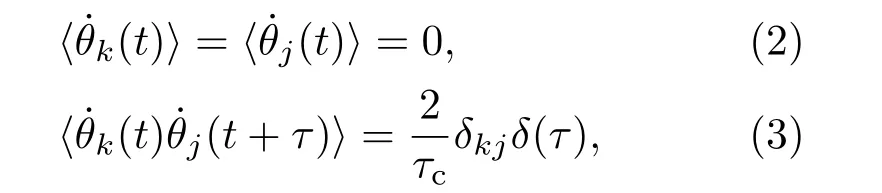
式中δkj代表克罗内克乘积,δ(τ)代表狄拉克δ函数.根据(1)式可得如下强度关联函数:

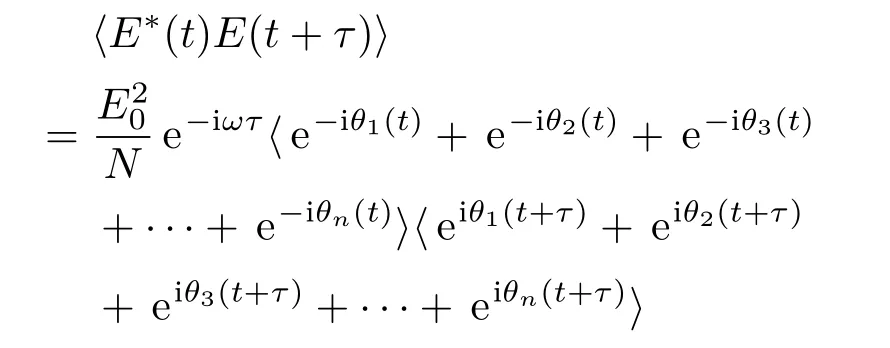
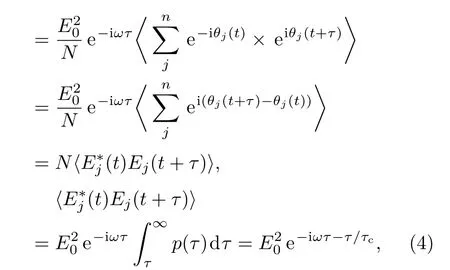
其中τc表示光场的相干时间.由此可推得混沌光场一阶相干度

进而可推导得出混沌光场的二阶相干度为

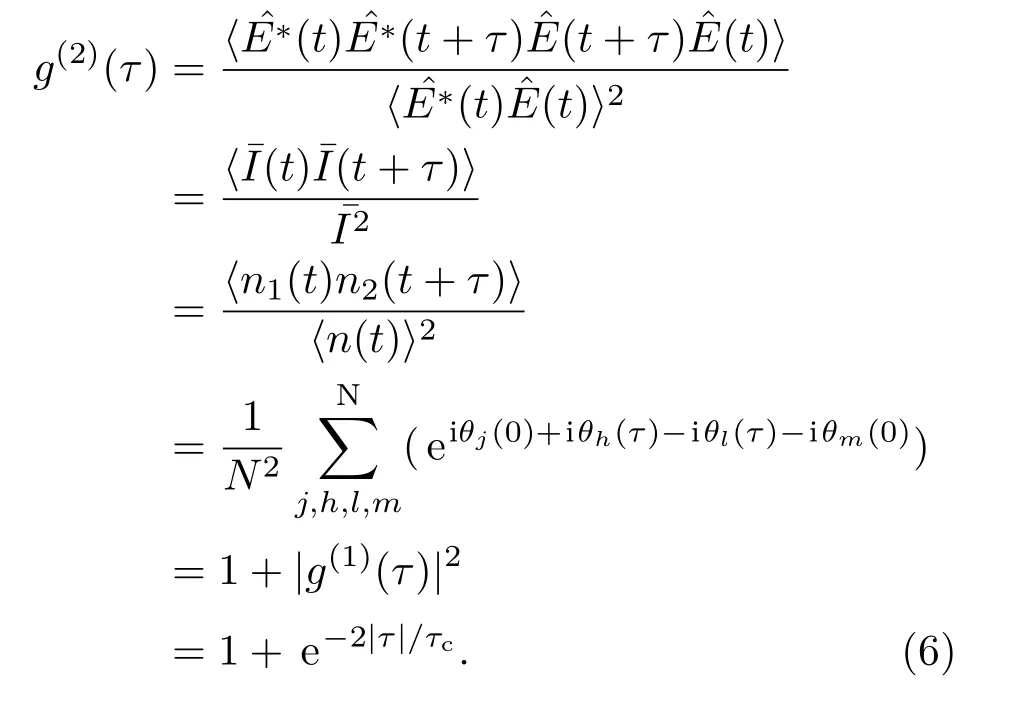
同理,利用上述类似的分析过程,可得到不同光场的二阶相干度,如热光场 (g(2)(τ)=1+exp(−τ2/τ2c),τc是热光场的相干时间)、相干光(g(2)(τ)=1)和单光子态

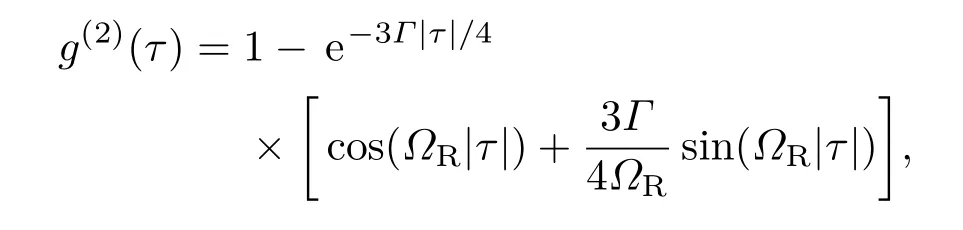
其中ΩR表示Rabi频率,Γ表示原子的自然线宽,如铯原子Γ=2π×4.57 MHz[21]的结果.由图1(a)可知,时间延迟在1.5 ns以内,根据混沌光场的相干长度,选取相干时间τc=0.6 ns[35],混沌光场和热光场随延迟时间的变化结果在零延迟附近二阶相干度大于1,呈现出明显的聚束效应;连续相干光的二阶相干度恒为1,不随延迟时间发生改变;而当ΩR/Γ=2时,单光子态的二阶相干度在零延迟附近呈现出Rabi振荡的反聚束效应.

根据Glauber-Sudarshan的P表象的理论,所有的光场都满足一定的光场或光子数分布[4],同时对随机变量及其统计特性的研究表明,真正理想的随机变量是高斯随机变量.故混沌光场的随机性可用高斯随机变量U来判别[36]:

对随机变量U进行傅里叶变换得到其概率密度函数,即光子数分布:

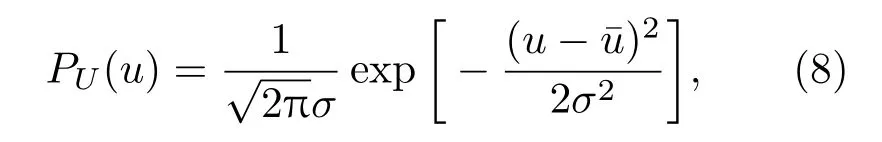
图1 (网刊彩色)不同光场的二阶相干度及光子数分布(a)相干时间τc=0.6 ns时,混沌光、相干光、热光场、单光子态的二阶相干度随延迟时间τ的变化;(b)平均光子数〈n〉=1.8时,服从高斯随机分布(蓝色实线)、泊松分布(绿色点划线)、玻色-爱因斯坦分布的(黑色短划线)光子统计分布曲线Fig.1.(color online)Second-order degree of coherence and photon number distribution of di ff erent optical fi eld:(a)Second-order degree of coherence of chaotic laser,coherent light,thermal light and single photon state versus delay time with 0.6 ns coherence time;(b)photon number distribution of Gaussian random(blue solid curve),Poisson(green dot-dashed curve)and BoseEinstein(black dashed curve)for 〈n〉=1.8.

其中〈n〉表示入射的平均光子数,m表示光子数.当入射光是单模热光场时,光子数分布服从玻色-爱因斯坦分布:

其中〈n〉表示入射的平均光子数.随着入射平均光子数〈n〉和光子数m的增大,上述分布可近似为

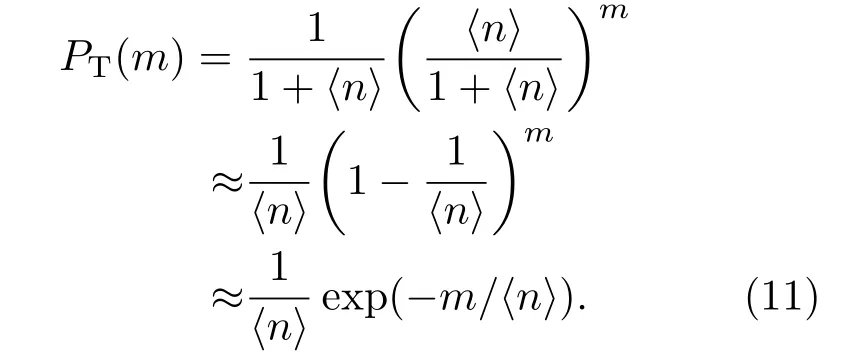
3 实验系统与结果分析

混沌光场二阶相干度及光子统计分布测量的实验装置如图2所示,混沌光源主要由一台分布式反馈半导体激光器DFB-LD(WTD LDM5S752)利用一个外腔光反馈系统构成.通过温度及电流控制将激光器DFB-LD中心波长稳定在1554 nm,其阈值电流为Ith=10.6 mA.激光器发出的光经过偏振控制器(polarization controller,PC)和环形器(optical circulator,OC)之后进入80:20的光纤耦合器( fi ber coupler,FC),80%的部分经过可变衰减器(variable attenuator,VA1)之后反馈回OC形成外腔延迟时间为125 ns的光反馈回路.

上述光反馈系统产生的混沌光场进入可编程光衰减器VA2(JW3301A),VA2可用来调节入射混沌光场的强度.从VA2输出的混沌光进入50:50的非偏振分束器(beam splitter,BS1)分成强度相等的两束:其中一束经过带宽为12 GHz的光电探测器(photodetector,PD,NEW FOCUS Model1554-B)转化为电信号,之后进入36 GHz带宽的实时示波器(oscilloscope,OSC,Lecroy LabMaster10-36Zi)或者26.5 GHz的频谱分析仪(RF spectrum analyzer,Agilent N9020 A,3 MHz RBW,3 kHz VBW)进行时序和频谱的动力学特性的分析;另一束进入分束器BS2分成50:50的两束.从BS2输出的两路光场,通过耦合透镜分别进入双通道单光子探测器(single photon detector,SPD,Aurea Technology LYNXEA.NTR.M2)的SPD1和SPD2,一路做start,另一路经过τ延时做stop.通过VA2控制入射进入单光子探测器的光强,测得对应光场的计数结果.随后两路信号进入数据采集系统,数据采集系统的最小分辨时间为65 ps,最大计数率为0.4 Mcounts/s,探测器的量子效率为25%.之后由数据采集系统对信号进行记录和相关处理,得到混沌光场的二阶相干度.

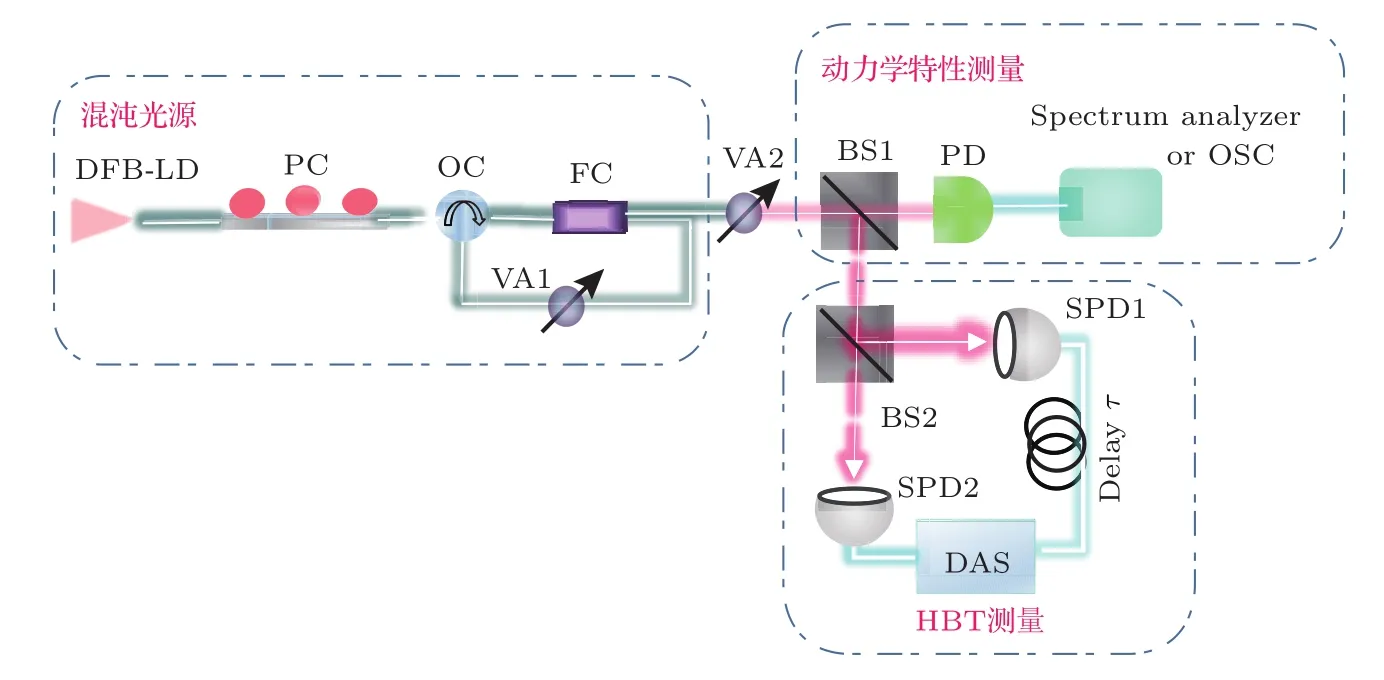
图2 (网刊彩色)混沌光场动力学特性及二阶相干度测量的实验装置图(DFB-LD,分布式反馈激光器;PC,偏振控制器;OC,环形器;FC,光纤耦合器;VA1,VA2,光衰减器;BS1,BS2,分束器;PD,光电探测器;OSC,示波器;Spectrum analyzer,频谱分析仪;SPD,单光子探测器;DAS,数据采集系统)Fig.2.(color online)Schematic of the experimental setup for measuring dynamics and second-order degree of coherence of a chaotic laser(DFB-LD,distributed feedback laser diode;PC,polarization controller;OC,optical circulator;FC, fi ber coupler;VA1,VA2,variable attenuators;BS1,BS2,beam splitters;PD,a photodetector;OSC,oscilloscope;SPD,single photon detector;DAS,data acquisition system).

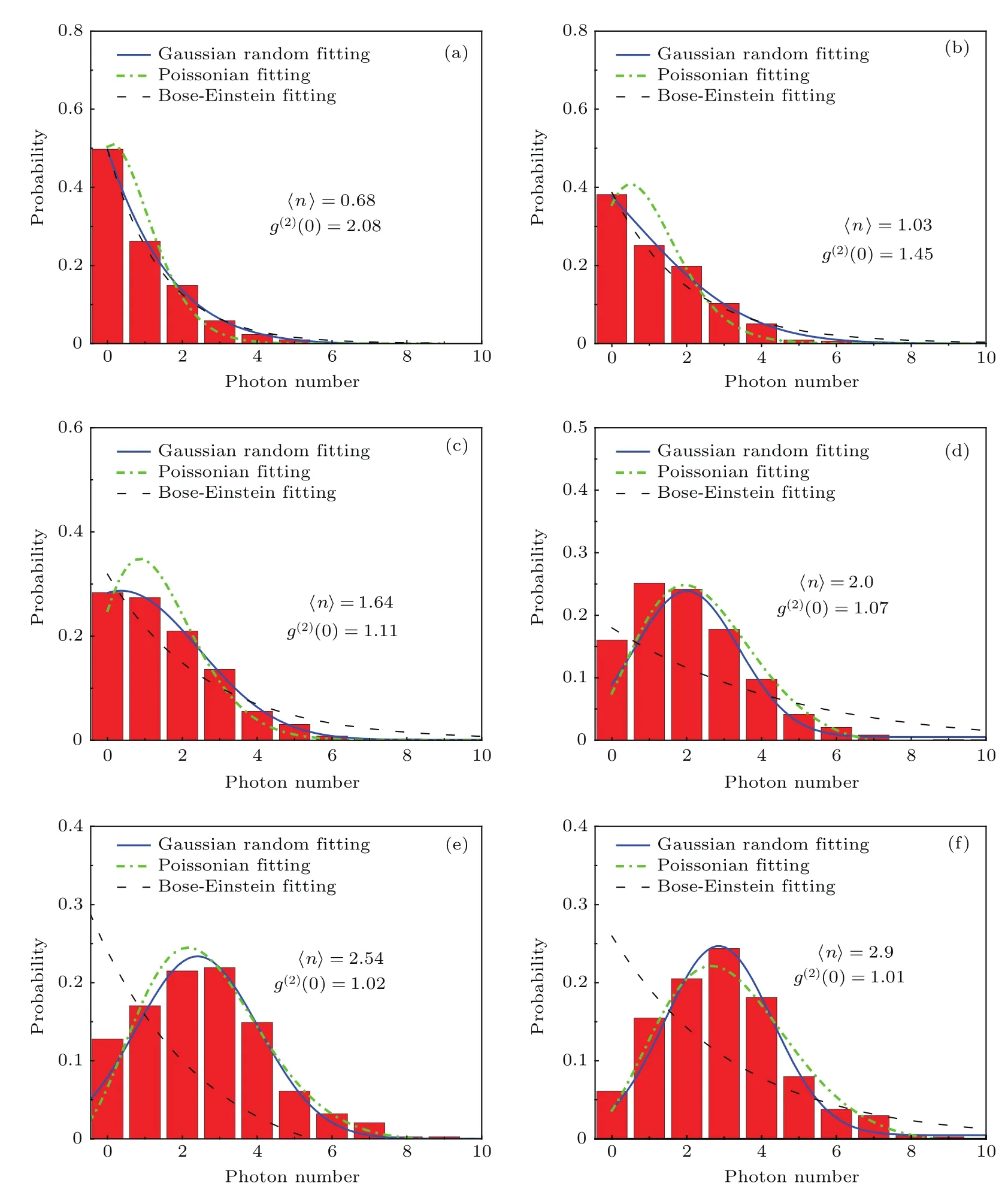
图3 (网刊彩色)混沌光场不同的光子数分布与g(2)(0)的测量结果,其中,红色直方图是实验结果;蓝色实线、绿色点划线、黑色短划线分别为对混沌光光子数分布进行高斯随机、泊松、玻色-爱因斯坦拟合的结果Fig.3.(color online)Di ff erent photon number distributions and g(2)(0)of chaotic laser.Red histograms represent experimental results.Blue solid,green dot-dashed and black dashed lines represent Gaussian random,Poissonian and Bose-Einstein fi tting respectively.

通过分别控制激光器的偏置电流(I=1.0Ith−2.0Ith)和反馈强度(0—10%),产生混沌光场,同时观测光场的频谱和时序,测量其对应的二阶相干度g(2)(0).根据上述测量结果,不同的反馈强度和偏置电流得到不同混沌光场的动力学特性.当偏置电流I=1.5Ith,反馈强度(feedback strength)γ=1.1%时,根据80%的带宽定义可得产生的混沌频谱宽度约为6.7 GHz.在此条件下,通过改变入射光强,测量了不同光子数分布的混沌光场及对应的零延时二阶相干度g(2)(0),测量结果如图3所示.图中红色直方图是去除背景噪声后实验测得的不同光子数分布的结果,蓝色实线、绿色点划线、黑色短划线分别为采用高斯随机分布、泊松分布、玻色-爱因斯坦分布对实验进行理论拟合的结果.在入射平均光子数较小(〈n〉=0.88,1.24,1.64)时,如图3(a)—(c)所示,采用高斯随机分布理论拟合得到的平均光子数分别为〈n〉=0.81,1.23,1.54,采用玻色-爱因斯坦分布理论拟合得到的平均光子数分别为〈n〉=1.01,1.40,1.82,而采用泊松分布理论拟合的结果与实验结果偏差较大.随着入射平均光子数的逐渐增大(〈n〉=2.0,2.54,2.9),如图3(d)—(f)所示,采用高斯随机分布拟合的平均光子数分别为〈n〉=1.80,2.35,2.67,采用泊松分布理论拟合的平均光子数为〈n〉=2.46,2.67,3.17,而采用玻色-爱因斯坦分布理论拟合结果已经偏离实验结果.综合上述结果,在入射平均光子数较小时,采用高斯随机分布和玻色-爱因斯坦分布得到的拟合结果与实验结果符合较好,而当平均光子数较大时,采用高斯随机分布和泊松分布得到的拟合结果与实验结果符合较好.随着平均光子数的逐渐增大,多光子概率相对于单光子概率增加更快,即多光子在探测时间中所占权重增加.同时由于探测多光子的响应时间小于单光子响应时间,所以探测器的响应时间会随着光子数的增加而减小,从另外一角度说明,随响应时间的缩短,同样探测条件下一定程度上增大了探测器的取样时间,当取样时间远大于光场的相干时间时,混沌光场逐步过渡到一种平稳的相干光场,因此出现随着平均光子数的增大,光子数分布由玻色-爱因斯坦分布逐渐过渡到泊松分布.而在整个过程中高斯随机分布的拟合与实验结果最为接近.同时平均光子数从〈n〉=0.88到〈n〉=2.9的变化过程中,测量得到的g(2)(0)由2附近减小,逐渐趋于1,而从图1(a)的理论分析可知理想混沌光场的g(2)(0)为2.这一结果主要是由于入射光增强时,探测器对多光子的响应能力有限,随着光场的平均光子数增大,更多的双光子或多光子在同一时刻进入探测器的概率增大,多光子响应时间影响增大,而探测器不能同时响应多个光子,测量得到的多光子信息就会降低,而这些多光子信息反映光子的聚束效应,因此测量得到的混沌光场的二阶相干度会随着平均光子数的增加而降低.

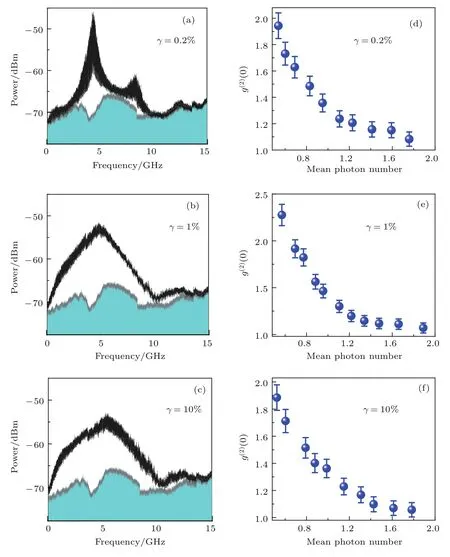
图4 (网刊彩色)不同反馈强度下混沌光场的(a)—(c)频谱图和(d)—(f)二阶相干度g(2)(0)的结果Fig.4.(color online)(a)–(c)Measured power spectra and(d)–(f)second-order degree of coherence g(2)(0)of chaotic laser in di ff erent feedback strengths.

在不同的偏置电流和反馈强度下,混沌光场呈现出不同的动力学特性,其对应的二阶相干度也有所不同.故根据上述测量结果,首先将偏置电流固定在I=1.5Ith,通过改变反馈强度来观测不同混沌态的动力学及光子统计特性.图4为反馈强度分别为0.2%,1%以及10%时,光场的频谱和二阶相干度的实验结果.图4(a)—(c)分别为三种反馈强度下对应的频谱.图4(a)为激光器的输出进入准周期状态;图4(b)为激光器的输出进入混沌状态,激光器的光谱线宽急剧展宽;图4(c)为反馈强度增至10%,此时激光器的线宽变窄,混沌减弱.激光器按80%能量带宽定义计算,其频谱宽度分别5.3,6.7和7.8 GHz.激光器的输出进入混沌状态,且线宽展宽的情况下,其带宽为6.7 GHz.图4(d)—(f)分别为三种反馈强度下二阶相干度随平均光子数的变化情况,可以看到:反馈强度较弱(0.2%)时,频谱会出现多个尖峰,并未进入完全的混沌状态,在平均光子数为0.53时二阶相干度g(2)(0)=1.943±0.097,随着平均光子数的增大g(2)(0)逐渐趋于1,当平均光子数为1.76时g(2)(0)=1.083±0.054;随着反馈强度增强至1%,频谱变得平滑,并且混沌的带宽展宽至6.7 GHz,在平均光子数为0.56时二阶相干度g(2)(0)=2.276±0.114,并随着平均光子数的增大g(2)(0)逐渐降低,在平均光子数为1.89时g(2)(0)=1.070±0.053;当反馈强度继续增强,达到10%时,在平均光子数为0.52的二阶相干度g(2)(0)=1.885±0.094,同样g(2)(0)逐渐趋于1,在平均光子数为1.78时g(2)(0)=1.057±0.052.出现上述现象一方面是由于前述的单光子探测器对多光子信息响应的降低或缺失,另一方面随着光强的增加,光场及光路中的杂散光和额外噪声随之增大,进而会减小光场的聚束效应,使二阶相干度逐渐趋于1.

图5 (网刊彩色)不同偏置电流且反馈强度为24%时,(a)—(c)混沌光场的时序和(d)—(f)二阶相干度g(2)(0)的结果Fig.5.(color online)(a)–(c)Temporal waveformand and(d)–(f)second-order degree of coherence g(2)(0)of chaotic laser with γ=24%and diferent injection currents.

在之前研究的基础上,为了更清楚地观测混沌快速时域动力学演化过程及对应的光子统计特性,当偏置电流接近于阈值电流,反馈强度在5.6%到66.0%范围内,激光器的输出呈现LFF状态.我们测量了偏置电流在阈值附近(I=1.07Ith−1.2Ith),反馈强度在24%,不同状态混沌光场的时序及对应的g(2)(0).图5所示为三种不同偏置电流(I=1.07Ith,1.12Ith,1.2Ith)下混沌光场的时序(图5(a)—(c)),以及与之对应的二阶相干度(图5(d)—(f))的结果.从图5可知,光场的时序变化从图5(a)的LFF和稳态(stable emission)共存状态,到图5(b)的持续LFF状态,最后进入图5(c)的CC状态.在光场由LFF进入CC状态时,振荡加快并且光谱明显展宽,同时测量了该过程中光场的二阶相干度.从图5(d)—(f)可以看出,在平均光子数为0.5左右时,三种状态下光场均呈现明显的聚束效应.同样由于多光子信息的缺失和额外杂散光的影响,随着平均光子数的增大,光场的聚束效应逐渐减弱,二阶相干度趋于1.由此可知,要准确地测量光场的光子统计特性及聚束效应,需要将入射的平均光子数控制在合适的区间并尽量降低背景和其他杂散光的影响.

4 结 论

基于HBT测量方案,对光反馈半导体激光器产生的混沌光场的光子统计分布和二阶相干度进行了理论和实验研究.测量了混沌光场不同入射平均光子数下的光子数分布和二阶相干度,并对光场的光子数分布进行了理论拟合对比分析,发现光场的光子数分布随着平均光子数的增加,会从玻色-爱因斯坦分布逐渐过渡到泊松分布,但在整个过程中始终满足高斯随机分布并符合较好.在此基础上,通过控制偏置电流和反馈强度,分析对比了不同状态的混沌光场的动力学特性及其二阶相干度的变化情况.结果表明,当平均光子数处在0.5—1区间,可以观察到不同状态混沌光场显著的聚束效应,随着光强增大至2.0附近,光场的二阶相干度逐渐趋于1.并对此结果给出了相应的物理解释.该实验表明,通过降低背景噪声和其他杂散光的影响,同时选择合适的实验条件,利用该实验方案可以准确测量混沌光场的二阶相干度和光子统计分布.该研究方法为判别混沌光场提供了新的研究视角,并且为混沌光场在随机数和保密通信等方面的应用以及下一步深入探究混沌光场的应用价值奠定了研究基础.

[1]Loudon R 2000 The Quantum Theory of Light(USA:Oxford Science Publications)p92

[2]Hanbury-Brown R,Twiss R Q 1956 Nature 177 27

[3]Glauber R J 1963 Phys.Rev.130 2529

[4]Glauber R J 1963 Phys.Rev.Lett.10 84

[5]Arecchi F T 1965 Phys.Rev.Lett.15 912

[6]Arecchi F T,Gatti E,Sona A 1966 Phys.Lett.20 27

[7]Morgan B L,Mandel L 1966 Phys.Rev.Lett.16 1012

[8]Kimble H J,Dagenais M,Mandel L 1977 Phys.Rev.Lett.39 691

[9]Short R,Mandel L 1983 Phys.Rev.Lett.51 384

[10]Had fi eld H R 2009 Nat.Photon.3 696

[11]Pan J W,Chen Z B,Lu C Y,Weinfurter H,Zeilinger A,Żukowski M 2012 Rev.Mod.Phys.84 777

[12]Banaszek K,Demkowicz-Dobrzaski R,Walmsley I A 2009 Nat.Photon.3 673

[13]Zhai Y H,Chen X H,Zhang D,Wu L A 2005 Phys.Rev.A 72 043805

[14]Paul H 1982 Rev.Mod.Phys.54 1061

[15]Zhang S H,Gao L,Xiong J,Feng L J,Cao D Z,Wang K 2009 Phys.Rev.Lett.102 073904

[16]Schultheiss V H,Batz S,Peschel U 2016 Nat.Photon.10 106

[17]Liu X F,Yao X R,Li M F,Yu W K,Chen X H,Sun Z B,Wu L A,Zhai G J 2013 Acta Phys.Sin.62 184205(in Chinese)[刘雪峰,姚旭日,李明飞,俞文凯,陈希浩,孙志斌,吴令安,翟光杰2013物理学报62 184205]

[18]Ryczkowski P,Barbier M,Friberg A T,Dudley J M,Genty G 2016 Nat.Photon.10 167

[19]Magaña-Loaiza O S,Mirhosseini M,Cross R M,Hashemi Rafsanjani S M,Boyd R W 2016 Sci.Adv.2 e1501143

[20]Diao W T,He J,Liu B,Wang J Y,Wang J M 2014 Acta Phys.Sin.63 023701(in Chinese)[刁文婷,何军,刘贝,王杰英,王军民2014物理学报63 023701]

[21]Guo Y Q,Li G,Zhang Y F,Zhang P F,Wang M J,Zhang T C 2012 Sci.China:Phys.Mech.Astron.55 1523

[22]Soriano M C,García-Ojalvo J,Mirasso C R,Fischer I 2013 Rev.Mod.Phys.85 421

[23]Wang S T,Wu Z M,Wu J G,Zhou L,Xia G Q 2015 Acta Phys.Sin.64 154205(in Chinese)[王顺天,吴正茂,吴加贵,周立,夏光琼2015物理学报64 154205]

[24]Argyris A,Syvridis D,Larger L,Annovazzi-Lodi V,Colet P,Fischer I,Garcia-Ojalvo J,Mirasso C R,Pesquera L,Shore K A 2005 Nature 438 343

[25]Reidler I,Aviad Y,Rosenbluh M,Kanter I 2009 Phys.Rev.Lett.103 024102

[26]Wang A B,Li P,Zhang J G,Zhang J Z,Li L,Wang Y C 2013 Opt.Express 21 20452

[27]Yoshimura K,Muramatsu J,Davis P,Harayama T,Okumura H,Morikatsu S,Aida H,Uchida A 2012 Phys.Rev.Lett.108 070602

[28]van Wiggeren G D,Roy R 1998 Science 279 1198

[29]Uchida A,Amano K,Inoue M,Hirano K,Naito S,Someya H,Oowada I,Kurashige T,Shiki M,Yoshimori S,Yoshimura K,Peter Davis P 2008 Nat.Photon.2 728[30]Kanter I,Aviad Y,Reidler I,Cohen E,Rosenbluh M 2010 Nat.Photon.4 58

[31]Tang X,Wu J G,Xia G Q,Wu Z M 2011 Acta Phys.Sin.60 110509(in Chinese)[唐曦,吴加贵,夏光琼,吴正茂2011物理学报60 110509]

[32]Li N Q,Kim B,Locquet A,Choi D,Pan W,Citrin D S 2014 Opt.Lett.39 5949

[33]Albert F,Hopfmann C,Reitzenstein S,Schneider C,Hö fl ing S,Worschech L,Kamp M,Kinzel W,Forchel A,Kanter 2011 Nat.Commun.2 366

[34]Lebreton A,Abram I,Braive R,Sagnes I,Robert-Philip I,Beveratos A 2013 Phys.Rev.A 88 013801

[35]Kong L Q,Fan L L,Wang A B,Wang Y C 2009 Acta Phys.Sin.58 7680(in Chinese)[孔令琴,樊林林,王安邦,王云才2009物理学报58 7680]

[36]Gooodman J W 2000 Statistical Optics(New York:Wiley-Interscience)p34

PACS:05.45.Gg,42.55.Px,42.50.ArDOI:10.7498/aps.66.120502

Photon number distribution and second-order degree of coherence of a chaotic laser:analysis and experimental investigation∗

Lan Dou-Dou1)2)Guo Xiao-Min1)2)Peng Chun-Sheng1)2)Ji Yu-Lin1)2)Liu Xiang-Lian1)2)Li Pu1)2)Guo Yan-Qiang1)2)†

1)(Key Laboratory of Advanced Transducers and Intelligent Control System,Ministry of Eduction,Taiyuan University of Technology,Taiyuan 030024,China)
2)(Institute of Optoelectronic Engineering,College of Physics and Optoelectronics,Taiyuan University of Technology,Taiyuan 030024,China)

24 January 2017;revised manuscript

27 March 2017)

The researches on higher-order coherence and quantum statistics of light fi eld are the important researching issues in quantum optics.In 1956,Hanbury-Brown and Twiss(HBT)(Hanbury-Brown R,Twiss R Q 1956 Nature 177 27)revolutionized optical coherence and demonstrated a new form of photon correlation.The landmark experiment has far-reaching in fl uenced and even inspired the quantum theory of optical coherence that Glauber developed to account for the conclusive observation by HBT.Ever since then,the HBT e ff ect has motivated extensive studies of higher-order coherence and quantum statistics in quantum optics,as well as in quantum information science and cryptography.Based on the HBT scheme,the degree of coherence and photon number distribution of light fi eld can be derived from correlation measurement and photon counting technique.With the rapid development of the photoelectric detection technology,single-photon detection,which is the most sensitive and very widespread method of optical measurement,is used to characterize the natures of light sources and indicate their di ff erences.More recently,HBT scheme combined with single-photon detection was used to study spatial interference,ghost imaging,azimuthal interference e ff ect,deterministic manipulation and detection of single-photon source,etc.

Due to broadband RF spectrum,noiselike feature,hypersensitivity to the initial conditions and long-term unpredictability,chaotic laser meets the essential requirements for information security and cryptography,and has been developed in many applications such as chaos-based secure communications and physical random number generation,as well as public-channel secure key distribution.But the research mainly focused on macroscopic dynamics of the chaotic laser.Moreover,the precision of measurement has reached a quantum level at present.Quantum statistcs of light fi eld can also uncover profoundly the physical nature of the light.Thus,it is important to exploit the higher-order degree of coherence and photon statistics of chaotic fi eld,which contribute to characterizing the fi eld and distinguishing it from others.

In this paper,photon number distribution and second-order degree of coherence of a chaotic laser are analyzed and measured based on HBT scheme.The chaotic laser is composed of a distributed feedback laser diode with optical feedback in fi ber external cavity con fi guration.The bandwidth of the chaotic laser that we obtain experimentally is 6.7 GHz.The photon number distribution of chaotic laser is fi tted by Gaussian random distribution,Possionian distribution andBose-Einstein distribution.With the increase of the mean photon number,the photon number distribution changes from Bose-Einstein distribution into Poissonian distribution and always accords with Gaussian random distribution well.The second-order coherence g(2)(0)drops gradually from 2 to 1.By changing the bias current(I=1.0Ith−2.0Ith)and feedback strength(0–10%),we compare and illustrate di ff erent chaotic dynamics and g(2)(0).From low frequency fl uctuation to coherence collapse,the chaotic laser shows bunching e ff ect and fully chaotic fi eld can be obtained at the broadest bandwidth.Furthermore,the physical explanation for sub-chaotic or weakening of bunching e ff ect is provided.It is concluded that this method can well reveal photon statistics of chaotic laser and will open up an avenue to the research of chaos with quantum optics,which merges two important fi elds of modern physics and is extremely helpful for the high-speed remote chaotic communication.

chaotic laser,second-order degree of coherence,single photon counting,semiconductor laser

10.7498/aps.66.120502

∗国家自然科学基金(批准号:61405138,61505136,61505137,61671316)、国家国际科技合作专项(批准号:2014DFA50870)和山西省自然科学基金(批准号:201601D011015,201601D021021)资助的课题.

†通信作者.E-mail:guoyanqiang@tyut.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.61405138,61505136,61505137,61671316),the Funds for International Science and Technology Cooperation Program of China(Grant No.2014DFA50870),and the Shanxi Nature Science Foundation of China(Grant Nos.201601D011015,201601D021021).

†Corresponding author.E-mail:guoyanqiang@tyut.edu.cn