基于MULTI2D-Z程序的Z箍缩动态黑腔形成过程模拟∗

陈忠旺 宁成

(北京应用物理与计算数学研究所,北京 100088)

基于MULTI2D-Z程序的Z箍缩动态黑腔形成过程模拟∗

陈忠旺 宁成†

(北京应用物理与计算数学研究所,北京 100088)

(2016年12月26日收到;2017年4月12日收到修改稿)

对辐射流体力学程序MULTI-2D进行改造,增加磁场演化方程程序模块,自洽地在运动方程模块中增加洛伦兹力,在能量方程模块中增加欧姆加热,将它改造成辐射磁流体力学程序MULTI2D-Z.验证了新增磁场程序模块的可靠性,并发现温度和密度的增大会抑制磁场的扩散,负径向速度梯度的流体对流也会抑制磁场的扩散.利用改造好的MULTI2D-Z程序模拟了峰值为8 MA的脉冲电流驱动的钨丝阵Z箍缩动态黑腔形成过程.得到了X光功率(约30 TW)和能量(约300 kJ)、泡沫辐射温度(约120 eV)、箍缩轨迹等模拟结果.在动态黑腔形成过程中,磁场主要分布在钨主体等离子体中;辐射向内传播,烧蚀泡沫柱而使它膨胀;辐射热波在被撞击的泡沫柱中传播,其传播速度比物质温度传播得快,当辐射热波传播到中心轴时泡沫柱中的辐射场变得比较均匀,并且除了冲击波处外辐射温度与物质温度基本上没有分离.这些模拟结果可增强人们对磁场扩散和对流规律以及动态黑腔形成机制的理解,同时表明了MULTI2D-Z程序可成为Z箍缩及其应用的新的程序模拟工具.

Z箍缩,动态黑腔,辐射磁流体,MULTI-2D程序

1 引 言

Z箍缩(Z-pinch)是由驱动电流产生的强磁场作用于自身载流等离子体(负载)上,使其受洛伦兹力作用而向轴心内爆的物理过程.当等离子体箍缩到心滞止时,产生高温高密度等离子体,并辐射出很强的X光,形成等离子体强辐射源.这类强X光辐射源在惯性约束聚变、实验室天体物理、材料辐射特性和辐射效应等研究领域有着广泛的应用[1].

近二十年来,国内外的Z箍缩实验和数值模拟研究均取得了很大的进展.国内在“强光一号”和“聚龙一号”(PTS)等脉冲功率装置上进行了大量的丝阵Z箍缩实验研究[2−5].在美国Sandia实验室的Z装置上进行的丝阵实验中,产生了峰值功率200 TW、能量2 MJ、脉宽5 ns的X射线脉冲,能量转换效率高达15%[6−8].在英国帝国理工大学的Magpie装置上也进行了大量的丝阵Z箍缩基础物理实验研究,发展了多种先进的诊断技术,对丝阵消融和内爆的细致物理过程进行了深入的观察和研究[9−11].

在Z箍缩的诸多应用中,其驱动惯性约束聚变应用研究是最令人瞩目的.在Z箍缩间接辐射驱动惯性约束聚变的概念设计中,需要形成一个黑腔为氘氚的靶丸内爆创造一个尽可能均匀、对称的辐射环境.目前人们提出了三种通过Z箍缩而形成的黑腔,即双端驱动黑腔、静态壁黑腔和动态黑腔[12].前两种黑腔的辐射源和靶丸相对分离,其辐射场的对称性均比较好,大体上能满足惯性约束聚变对辐射场对称性的要求,但其能量耦合效率较低,需要相对较高的驱动电流才能达到聚变点火条件.在动态黑腔的形成中,其核心思想是利用单层或者双层丝阵Z箍缩內爆等离子体撞击内置的中心泡沫塑料柱,內爆等离子体撞击塑料泡沫柱时损失的动能以及形成的冲击波产生辐射,这些辐射在泡沫柱中传播和均匀化,并且被外面高Z丝阵等离子体俘获,而在靶丸的周围形成一个受约束的辐射环境.因为它是在丝阵內爆动态过程中形成的,故称其为动态黑腔.在动态黑腔中Z箍缩内爆等离子体、动能-X光能量转换体(泡沫柱)和聚变靶丸等紧密地耦合在一起,从而使它们之间的能量耦合效率比较高,进而可能在驱动电流水平较低的Z箍缩装置上实现惯性约束聚变点火.目前动态黑腔成了Z箍缩间接驱动惯性约束聚变的主要技术途径之一[13].

Z装置上的动态黑腔实验[14,15]表明:泡沫柱的密度由15 mg/cc被压缩到了35 mg/cc,而电子温度由400 eV因辐射降到了300 eV;受冲击压缩的泡沫等离子体产生了大于180 kJ的辐射能量,其中靶丸吸收了超过40 kJ的辐射能量,而此能量已是靶丸点火所需能量的1/4;冲击波对称性受内爆等离子体不均性和不稳定性的影响较小,从而有利于中心聚变靶丸实现球对称辐射烧蚀内爆压缩.此外在Z装置上还首次进行了利用Z箍缩动态黑腔驱动充氘气靶丸出中子的实验[16],产生了1×1010—5×1010个热核中子.

美国著名的激光惯性约束聚变模拟程序LASNEX已增加了磁场模块,已应用于Z箍缩驱动的惯性约束聚变物理研究[17,18].原来LASNEX程序是典型的三温(电子、离子和辐射温度)辐射流体力学程序,与国内大部分的激光惯性约束聚变和Z箍缩模拟程序的物理模型相似,所采用的计算方法也主要是拉格朗日流体算法.它在所增加的磁场模块中考虑了非理想磁场演化因素,如Hall效应和Nernst效应.在空间二维上它对动态黑腔中丝阵内爆到泡沫柱转换体和嵌套在泡沫柱中的靶丸内爆,以及电极板对辐射的吸收等过程进行了整体数值模拟[18].丝阵内爆时间在100 ns左右,而紧接着的靶丸内爆仅有几个纳秒.模拟得到的中子产额比实验测量的值大两倍,冲击波速度比测量值高30%,靶丸心部的气体温度比由光谱推测的值高.模拟结果再现了Z箍缩内爆到泡沫柱和紧接着产生的辐射冲击波过程,还预言了泡沫柱吸收等离子体早期因欧姆加热和内爆而产生的辐射所形成的消融冲击波,从而帮助人们更好地理解动态黑腔的形成过程.

在国内也开展了Z箍缩驱动动态黑腔的实验和数值模拟研究[5,19−21].目前已发表的主要是在驱动电流比较低的实验装置(如强光I号)上获得的实验结果,得到了径向和轴向的X光辐射功率、外边界的内爆轨迹、泡沫柱的发光图像等结果.数值模拟主要是在空间一维上再现了动态黑腔形成过程的主要物理特征,如各物质界面的内爆轨迹,密度、电子温度和辐射温度的时空演化及其相互关系,冲击波形成和传播过程等.

MULTI系列程序是西班牙的Ramis教授等开发的,用于模拟高能量密度等离子体中发生的辐射和物质相互作用过程,如激光惯性约束聚变中的激光-等离子体相互作用过程.最早的MUTLI一维程序是使用Fortran语言编写的,1994年Ramis教授开发了一种新的程序语言r94,用于编写MULTI程序.经过二十多年的发展,目前MUTLI系列程序有MULTI-IFE,MULTI-fs,MULTI-1D,MULTI-2D和MULTI-3D等版本.由于它们都是开源的,因此得到了比较广泛的应用[22−24].相对而言,一维和二维程序已发展得比较成熟.

动态黑腔负载是由柱对称的多层物质嵌套组合而形成,至少需要空间二维的物理模型才能比较好地描述动态黑腔的形成过程.因此,本文对国外开源的激光惯性约束聚变模拟程序MULTI-2D进行改造,使它们能应用于Z箍缩物理、Z箍缩驱动惯性约束聚变及其聚变能应用方面的物理研究.在物理模型上,它最大的特点是仅有一个物质温度,辐射温度是通过等离子体物质的辐射参数和近似辐射能流计算得到,因此,具有非常高的计算效率.它采用任意欧拉-拉格朗日算法和非结构三角形网格,能处理在内爆过程中产生的流体大变形,较好地避免在流体模拟中因网格畸变而无法继续计算的问题,以及能处理由不同几何构形部件组合而成的复杂的内爆物理问题.

2 物理模型和程序框架

采用辐射磁流体力学方程对等离子体Z箍缩动力学过程进行模拟[25,26].质量守恒方程为

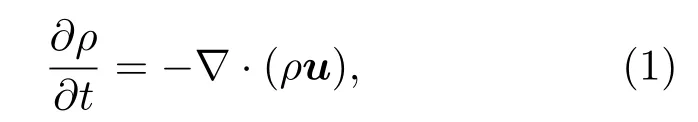
这里ρ是物质密度,u为流体速度,t为时间.

动量守恒方程为

其中p为总压强,包括流体压强和黏性;J×B为导电流体受到的单位体积洛伦兹力,J为电流密度,B为磁感应强度.在柱对称的Z箍缩中,可以仅考虑磁场的角向分量Bθ,此时,洛伦兹力在二维柱坐标系(r,z坐标系)下的表达式为

这里fr和fz分别表示f在r方向和z方向的分量.能量守恒方程为

式中,ε是流体单位质量内能;∇·(ρεu)表示单位时间流入流体单元的内能;p∇·u是压强做功;∇·F是热传导传输的能量;∇·S是辐射能流沉积;W是欧姆加热,其在二维柱坐标系下的表达式为

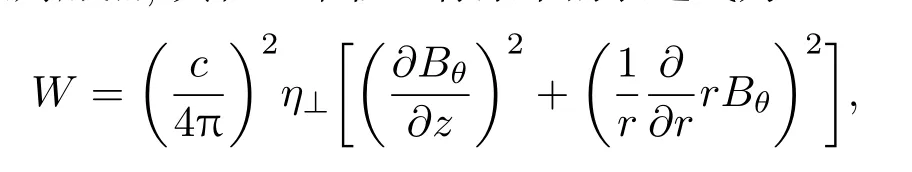
其中,η⊥为垂直于磁场方向的等离子体电阻率,c为光速.

在辐射输运中,流体速度远小于光速,在任一时刻,辐射场都可以认为是准静态的.在局部热力学平衡附近,忽略散射和折射,辐射输运方程为[23]

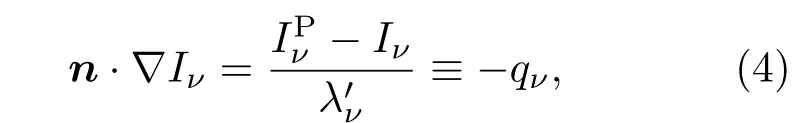
其中,n是传播方向;qν是单位体积辐射的沉积能;λ′ν为辐射频率为ν的辐射平均自由程,与材料的温度和密度有关[27];Iν是辐射强度;IPν是普朗克分布函数,

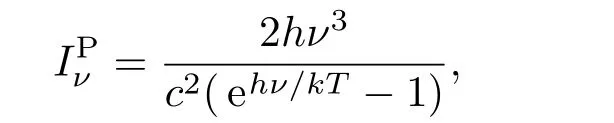
这里h和k分别是普朗克常数和玻尔兹曼常数,T为物质温度.若考虑单群方法处理辐射输运方程,则对所有频率积分就得到

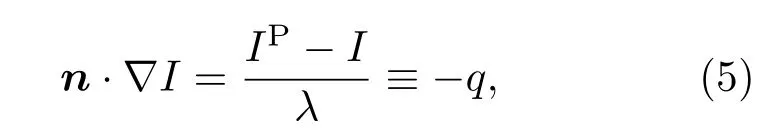
这里平均辐射自由程λ定义为

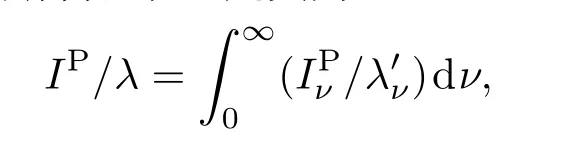
其中I,q和IP=σT4/π分别表示Iν,qν和IPν对所有频率的积分值;σ为Stefan-Boltzmann常数.在局部热力学平衡附近,考虑近似n·∇I≈n·∇IP,可得辐射强度近似表达式

从而可得辐射能流

利用辐射强度,空间某一点的辐射温度通过以下表达式进行计算:

磁场演化方程为

只考虑θ方向的磁场,在二维柱坐标系下(7)式变成

其中,uz,ur分别为流体沿着z和r方向的速度分量;磁扩散系数vm=η⊥c2/4π.平行磁场或无磁场下Spitzer电阻率η =1.15× 10−14z lnΛT−3/2(s),其中z为平均电离度.

本文利用实用的解析表达式来计算电离度.在Thomas-Fermi理论框架下,More提出了一个平均电离度计算公式[28].设ρ为质量密度,单位g/cm3,Te为电子温度,单位eV(约11605 K),Z为原子序数,A为相对原子质量.定义如下过程量R=ρ/(ZA),T0=Te/Z4/3,T1=T0/(1+T0),α =14.3139,β =0.6624,x= αQβ,f(x)=则平均电离度z=f(x)Z.其中Q的计算过程如下:

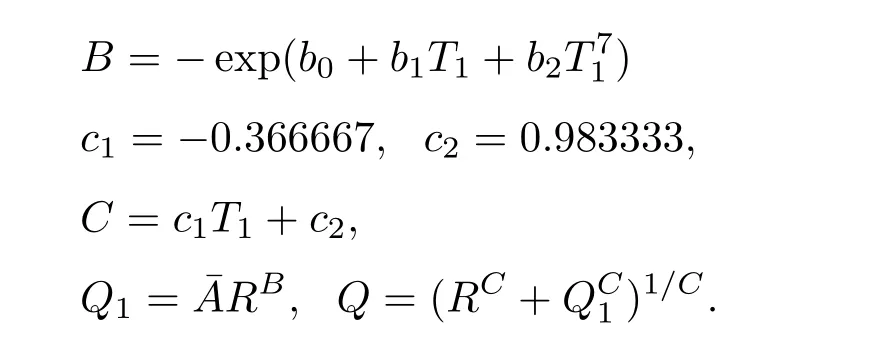
相对于原来MULTI-2D程序的物理模型,为了使它能模拟研究Z箍缩及其相关的物理问题,需要增加磁场演化方程,在动量守恒方程中添加洛伦兹力,在能量守恒方程的源项中添加欧姆加热项.此外,为了计算电阻率而增加一个电离度的解析计算表达式.这样就把它改造成了辐射磁流体力学程序,并仍然具有高的计算效率.

MULTI-2D是结构化程序,由若干相对独立的功能模块组成.这些模块包括流体模型建立模块、循环模块、数据输出和绘图模块,如图1所示.在流体模型建立模块中,包括网格生成、参数输入和数据初始化.在主体循环模块中,有外加驱动源、流体运动、能量输运以及状态方程等模块.驱动源是外加能量输入项,如激光辐射、重离子束注入,及本文增加的电流或磁场.能量模块包括物质能量方程,以及辐射输运、热传导和做功等的计算.状态方程采用QEOS程序生成的状态方程参数[29,30].

图1 MULTI-2D程序框架结构Fig.1.Programm frame of MULTI-2D.

MULTI-2D程序采用r94语言编写.该语言于1994年开发,是基于C语言的高级语言,适用于UNIX操作系统.它通过构建大量函数库而进行编程,使得程序精炼,可使用X窗口进行操作.

本文在MULTI-2D程序中加入磁场演化程序模块,在流体运动模块中加入洛伦兹力,在物质能量方程模块中加入欧姆加热,将它发展成二维辐射磁流体力学数值模拟程序MULTI2D-Z,并应用于Z箍缩动态黑腔形成过程的模拟研究.

3 模拟结果

3.1 磁场演化模块验证与磁场演化分析

为了验证所添加的磁场演化方程程序模块的正确性,考虑如图2所示的等离子体柱.横坐标轴为柱等离子体的对称轴(z轴),纵坐标轴为柱等离子体的半径(r轴).等离子体柱的初始半径为1.25 cm,半高度为0.5 cm.考虑的是钨等离子体,密度为8.6×10−4g/cm3,初始温度为1 eV.由于柱等离子体的对称性,因此,实际需要的计算区域仅为实线的右半部分.在z方向上加载8 MA的恒定电流,该电流在θ方向产生角向磁场,该磁场将向对称轴方向扩散演化.为了验证的方便,给定等离子体速度,不求解流体运动方程.此时,磁场的演化过程由方程(8)描述.磁场的边界条件为

其中rm为等离子体柱的径向边界,L为z方向边界.

明显地,该磁场演化过程可以由径向(r方向)一维磁场演化方程来描述.一维方程为

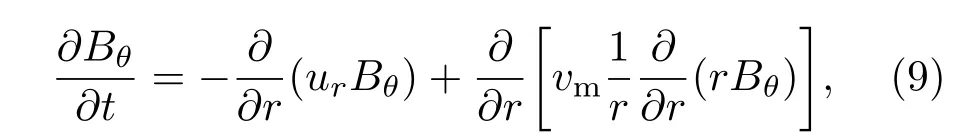
其边界条件为

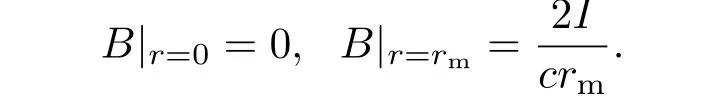
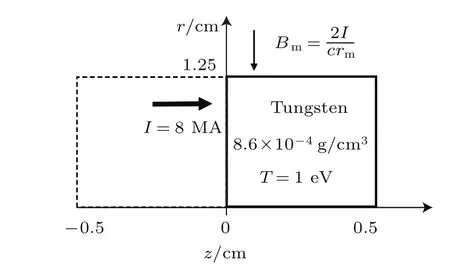
图2 磁场演化模块验证模型Fig.2.Plasma model for veri fi cation of magnetic fi eld evolution module.

一维磁场演化方程程序模块在柱对称Z箍缩等离子体的模拟中是普遍使用的,其磁场演化规律清楚,程序模块可靠.将由新添加的二维磁场演化方程程序模块模拟出的结果与一维磁场演化程序模拟的结果进行比较,就可以判断基于非结构网格上的新增磁场程序模块的正确性.当流体静止时,仅有纯磁扩散,而当存在流体运动速度梯度时,则磁场既有扩散,也有对流.下面就这两种情况对磁场演化模块和相应的磁场演化规律进行考察.

图3(a)是在假定流体静止时,当8 MA的恒定电流加载到该等离子体柱时,利用一维和二维磁场演化方程对其中磁场演化过程的模拟结果进行比较.恒定电流所产生的角向磁场仅随r而变化,磁场逐渐向中心轴扩散,并且很快就达到稳定分布.可见一维和二维的模拟结果符合得很好.

图3(b)给出的是在流体流动、并且存在速度梯度时,利用一维和二维磁场演化方程对该磁场演化过程的模拟结果.这里假定流体径向速度随半径的变小而下降,为某一径向位置,um=−5×106cm/s.磁场外边界值Bm=2I/crm随着流体向内箍缩运动而增大,磁场既随流体对流,又向内扩散.可见,此时二维和一维模拟结果也很好地重合,说明基于非结构网格上的新增二维磁场演化方程程序模块是正确的.

下面利用我们新增的基于非结构网格上的二维磁场演化方程程序模块来研究磁扩散系数和流体对流对磁场演化的影响.在模拟磁扩散系数对磁场演化的影响时,通过改变等离子体温度或密度而改变电阻率,使磁扩散系数发生变化.这里采用图2所示的基准等离子体温度或密度的100倍来改变电阻率(磁扩散系数),观察(100倍温度,基准密度),(基准温度,100倍基准密度)和(基准温度,基准密度)等三种情况下t=100 ns时的磁场分布情况.在考察流体对流对磁场演化的影响时,使等离子体处于三种运动状态,即零速度、恒定速度u1=um=−5×106cm/s和速度随半径变化,并假定磁场的边界值为恒定的Bm.为了描述磁场扩散或向轴心演化的快慢,我们定义一个磁场扩散速度.磁场向轴心扩散而逐渐减小,因此,定义磁场为Bm/e的位置r随时间变化率为磁场扩散速度(自然常数e=2.71828).

图4(a)是磁场扩散的模拟结果,可见密度变化对磁场分布的影响比较小,密度增加导致电离度减小,从而电阻率减小,磁扩散系数变小,进而抑制磁场的扩散;温度对磁场分布的影响比较复杂,虽然温度升高使电离度有增大的趋势,使得电阻率增大,但电阻率与T−3/2成正比,温度升高又使得电阻率下降得更快.综合起来,本模拟结果表明温度升高抑制了磁场的扩散,磁场更集中于等离子体柱的表面.这表明等离子体的导电性好,则电流更趋肤,是符合物理理解的.图5(a)是与图4(a)相同条件下的磁扩散速度随时间的变化情况.在电流加载的初始阶段,磁扩散速度比较大,但随着时间的增加,扩散速度快速下降,最后趋于零,即磁场分布趋于稳定.但等离子体温度较高时,磁扩散速度初始时相对较小,下降也缓慢,或者说磁扩散系数减小,磁场扩散速度减慢,需要更长的时间才能到达稳定.

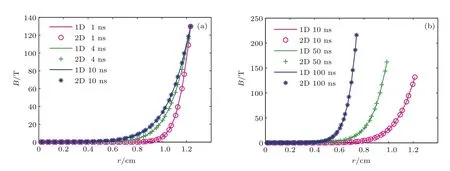
图3 (网刊彩色)二维磁场演化程序与一维磁场演化程序模拟得到的磁场径向分布演化的比较 (a)流体静止;(b)存在流体速度梯度Fig.3. (color online)The comparison of magnetic fi eld pro fi les in radial direction calculated byrtwodimensional and one-dimensional magnetic inductance equations:(a)ur=uz=0;(b)ur(ri)= ium,u=0.rmz

图4 (网刊彩色)磁场的分布演化 (a)流体静止时等离子体参数变化对磁场扩散的影响;(b)流体对流对磁场分布演化的影r响,u1表示等离子体以恒定速度um=−5×106cm/s向轴心运动,u2表示等离子体以空间变化速度ur(ri)=ium向轴心运动;边界磁场固定Bm=128 T rmFig.4.(color online)The evolutions of magnetic fi eld pro fi les:(a)The e ff ects of plasma parameters on the magnetic fi eld evolution when the the plasma is at rest;(b)the e ff ect of fl uid motion on the magnetic fi eld evolution when the plasma is moving towards the axis at a constant velocity um=−r5×106cm/s,which is denoted by u1,as well as the plasma is moving at a convective velocity ur(ri)=ium,which is denoted by u.The magnetic fi eld at boundary interface is fi xed,B=128 T.rm2m

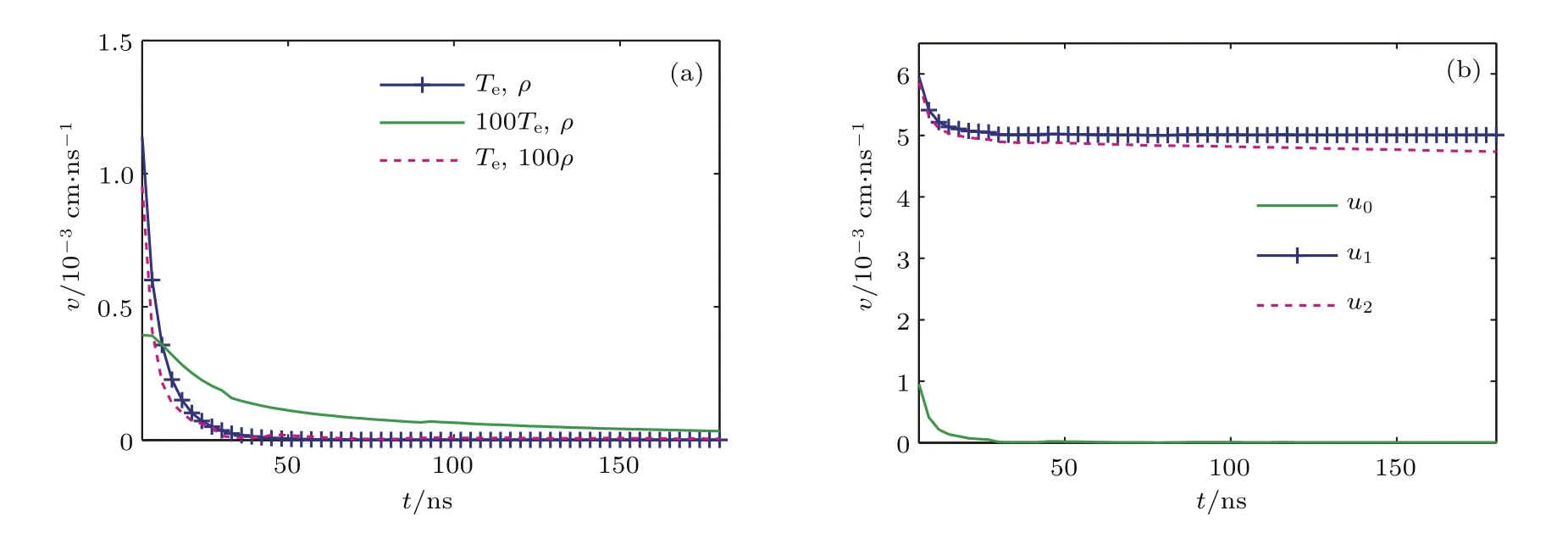
图5 (网刊彩色)磁场扩散速度随时间变化 (a)流体静止;(b)流体运动,uo表示流体静止;其他与图4中的情况相对应Fig.5.(color online)The variation of velocity of magnetic fi eld di ff usion with time:(a)The plasma is at rest;(b)the plamsa is moving at a certain velocity.The conditions used in the simulations are the same as that in Fig.4,besides the uowhich denotes the plasma at rest.

图4(b)是在等离子体运动的情况下磁场扩散的结果.当等离子体以恒定的速度向轴心运动时,磁场在不同时刻的径向分布是相似的(这是因为在拉氏坐标下当流体速度恒定均匀时,对流项消失,从而磁场扩散与流体静止时的情况一样),但随着等离子体的压缩,内部的磁场逐渐增大.当等离子体以随r逐渐减少的速度箍缩时,磁场的扩散效应减弱,磁场的分布更趋肤.表明此时的等离子体对流抑制了磁场的扩散,或者说在实际的Z箍缩中,在箍缩初始阶段已扩散进入等离子体中的磁场,当等离子体变得快速向心运动时,磁场将有向外反扩散而再趋肤的过程.图5(b)是与图4(b)相同条件下的磁扩散速度随时间的变化情况.有意思的是,当等离子体静止时磁扩散速度逐渐趋于零,而当它以恒定速度流动时磁扩散速度等于等离子体运动速度5×106cm/s,即磁场被冻结在等离子体中,随流体一起运动;当速度不恒定,存在负的速度梯度时,磁扩散速度略小于流体运动速度,这是因为此时的磁扩散被减弱了.

3.2 丝阵Z箍缩驱动的动态黑腔形成过程

新添加的磁场演化方程程序模块得到验证后,改造后MULTI-2D程序的驱动源除了原来的激光和粒子束外,又增加了磁场力,从而它就具有了模拟Z箍缩及其相关物理过程的能力.典型而简单的动态黑腔负载构形就是在丝阵的中心嵌入一根低密度泡沫柱(其组成成分为碳和氢,通常将它简记为CH),当在强脉冲电流的作用下丝阵内爆到泡沫柱,撞击泡沫柱而在泡沫柱中形成冲击波,丝阵和泡沫等离子体被热化,产生辐射向泡沫柱中心传播,在丝阵等离子体的部分约束下在泡沫等离子体中形成比较匀化的辐射场.为了能利用动态黑腔来驱动惯性约束聚变,这一整体动力学过程的发展、演化过程需要通过数值模拟(当然也需要实验)研究、理解清楚.

下面在二维柱坐标系下,利用改造完成的MULTI2D-Z程序对峰值电流为Im=8 MA的脉冲电流驱动的嵌套了中心泡沫柱的丝阵Z箍缩內爆过程进行模拟.

图7是计算得到的丝阵和泡沫柱的箍缩轨迹、X光功率和能量、丝阵和泡沫柱的收缩比、电流波形等随内爆过程的变化.整体箍缩到心在150 ns左右,X光功率峰值接近30 TW,总能量在330 kJ左右,丝阵和泡沫的最大压缩比分别为15和5左右.泡沫柱在被丝阵等离子体碰撞压缩以前,略微膨胀.

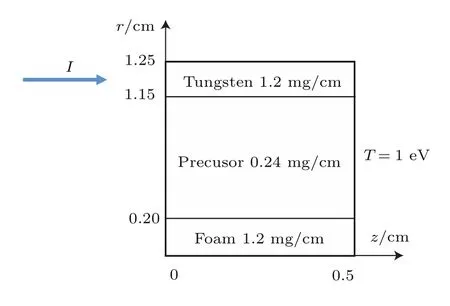
图6 动态黑腔负载模型Fig.6. The used model in simulation of dynamic hohlraum.

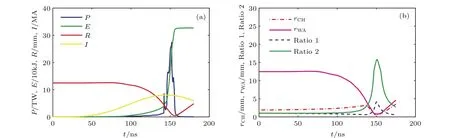
图7 (网刊彩色)动态黑腔形成过程中一些宏观参量随时间的变化 (a)丝阵外半径R、电流I、X光功率P和径向辐射能量E;(b)丝阵和泡沫的柱外半径(rWA,rCH),丝阵和泡沫柱的收缩比(Ratio 2,Ratio 1)Fig.7.(color online)The variations of some macroscopical quantities with time during the formation process of dynamic hohlraum:(a)Outer radius of wire-array(R),current(I),X-ray power(P)and energy(E);(b)outer radii of wire-array(rWA)and foam(rCH),convergence ratioes of wire-array(Ratio 2)and foam(Ratio 1).

图8—图10分别是丝阵等离子体内爆碰撞泡沫柱后三个时刻(146,150,152 ns)密度、等离子体温度和辐射温度、内爆速度、磁场、辐射场(温度)等的空间分布情况.t=146 ns时,丝阵内爆到了半径为0.3 cm的地方,离泡沫柱的初始位置还有0.1 cm.此时在丝阵等离子体中形成了很强的冲击波(见图8(a)—(c)中的密度尖峰位置),内爆速度达到了4×107cm/s,物质温度达到了370 eV左右,泡沫中的最大辐射温度接近100 eV,边界磁场达到约520 T.在靠近中心轴处的辐射温度比物质温度高,表明辐射热波向轴心方向传播比物质温度快.在箍缩过程中磁场主要分布在主体钨等离子体中,形成很强的磁压,使等离子体加速向内箍缩,在压缩做功和欧姆加热作用下,主体等离子体温度较高,密度较大.温度升高和密度增加使磁扩散系数减小,另外流体压缩也抑制磁场的扩散.高温高密度主体丝阵等离子体向泡沫内部和外表面及两端电极发射辐射,向内辐射加热烧蚀泡沫柱,使泡沫柱因温度升高而向外膨胀,此时,泡沫柱的外半径膨胀到了大约0.24 cm.向外表面(r方向)和电极(z方向)的辐射导致内爆等离子体的能量漏失,使得靠近电极板区域和等离子体外则的辐射温度均比较低.

到了150 ns(见图9),丝阵等离子体内爆到全部进入了原泡沫柱所在的区域,到达半径为0.17 cm的位置,表明泡沫柱已被丝阵等离子体碰撞,泡沫柱得到了一点压缩.此时在丝阵等离子体中的冲击波(见图9(a)—(c)中的密度尖峰位置)得到增强,温度和密度增高,但内爆速度下降了一点,最大内爆速度下降到3.7×107cm/s,物质温度升高到460 eV左右,泡沫中辐射温度在中心区域基本均匀化,其值达约120 eV,并且其中的物质温度和辐射温度几乎没有分离,达到了平衡,边界磁场超过了900 T.钨等离子碰撞低密度泡沫后形成物质冲击波,速度减缓,动能转换为内能,温度迅速升高,形成辐射冲击波;辐射冲击波迅速向内传播,在物质冲击波到来之前形成了较为均匀的黑腔辐射环境,黑腔中物质温度和辐射温度较为重合,温度达120 eV左右;与此同时,主体等离子体向外辐射出X光的第一个小波峰,功率在7 TW左右(见图7(a)).在动态黑腔概念设计中,希望在丝阵碰撞压缩泡沫柱到达靶丸之前,所形成的黑腔辐射场对靶丸的烧蚀压缩,并使其达到聚变点火条件.因此,碰撞后主体等离子的速度大幅度减小,损失的动能转化为内能和辐射,大部分辐射被泡沫吸收,这是黑腔辐射场形成的重要机制.

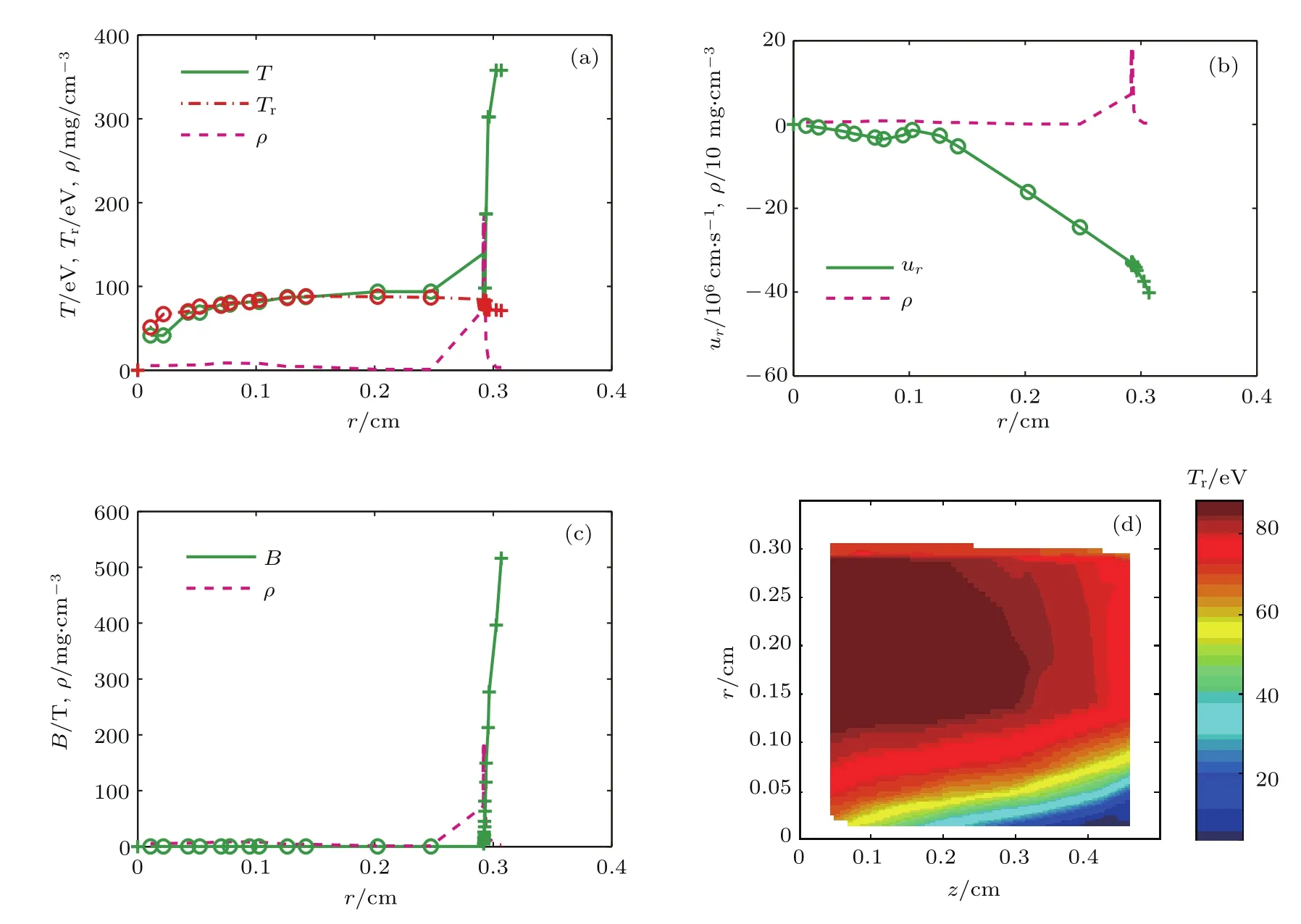
图8 (网刊彩色)146 ns时刻各参量的随空间分布 (a)辐射温度Tr、物质温度T和密度分布ρ;(b)速度ur和密度ρ分布;(c)磁场B和密度ρ分布;(d)辐射温度Tr空间分布Fig.8.(color online)The spatial pro fi les of some physical quantities at 146 ns:(a)Radiation,plamsa temperatures,and density pro fi les;(b)velocity and density pro fi les;(c)magnetic fi eld and density pro fi les;(d)spatial distribution of radiation temperature.The part of a line with symbols of circle belongs to foam,and it with symbols of plus belongs to wire-array.

图9 (网刊彩色)150 ns时各时刻参量随空间变化 (a)辐射温度、物质温度和密度分布;(b)速度和密度分布;(c)磁场和密度分布;(d)辐射温度空间分布Fig.9.(color online)The spatial pro fi les of some physical quantities at 150 ns:(a)Radiation,plamsa temperatures,and density pro fi les;(b)velocity and density pro fi les;(c)magnetic fi eld and density pro fi les;(d)spatial distribution of radiation temperature.The part of a line with symbols of circle belongs to foam,and it with symbols of plus belongs to wire-array.

t=152 ns以后,丝阵和泡沫等离子体继续箍缩,泡沫等离子体整体得到进一步的加速,泡沫中的温度和密度进一步增大,在泡沫中出现小的密度峰,中心附近的辐射和物质温度稍高.由于磁压力做功,使得泡沫的温度和辐射温度继续增加,最高达到约170 eV,它们仍然基本上没有分离.辐射温度在r方向分布的均匀性变弱(见图10(a)),但对比图9(d)可以看到,高温和比较均匀的辐射区域在z方向有所增大.由于边界辐射温度的增大,使得边界辐射能量以更高的速率损失(辐射能流约为导致径向辐射温度相对更低.因此,对于动态黑腔驱动聚变靶丸的实际应用而言,需要根据驱动电流、靶丸大小仔细地设计动态黑腔的负载构形,以明确能够利用的动态黑腔中辐射场的时间窗口和空间区域,使其靶丸实现对称压缩和点火成功.在整体箍缩到心时,等离子体减速滞止,产生强烈的X光辐射,此时X光辐射脉冲的峰值功率达约28 TW.

在径向一维上密度、物质温度(电子温度)和辐射温度的空间分布和随时间的演化关系的整体特征,如丝阵等离子体的前期膨胀、辐射烧蚀泡沫柱而膨胀、辐射热波传播较快、辐射热波与辐射冲击波的空间分离等,与一维拉氏非平衡辐射磁流体力学程序CRMHA的模拟结果[20]以及国外的模拟结果[18]都是相似的.并且预期的黑腔辐射温度与文献[20]的结果也接近,都是120 eV左右.说明MULTI2D-Z程序模拟动态黑腔形成过程所得到的物理结果是基本正确、可靠的.但本文中泡沫柱的辐射温度的均匀化过程要慢一些,即泡沫等离子体的辐射吸收更强烈一些,并且本文能给出辐射场在径向和轴向方向上的均匀化情况.

4 结 论

从辐射磁流体力学基本方程出发,通过在MULTI-2D程序中增加磁场演化方程程序模块,同时自洽地在流体动量守恒方程中增加导电流体所受到的洛伦兹力,在能量守恒方程中增加欧姆加热能量源项,并在相应的程序中进行改动.通过新增程序模块的验证,使得MULTI-2D程序改造、发展成了MULTI2D-Z程序,成为基于非结构网格的二维辐射磁流体力学程序,可以应用于Z箍缩驱动的动态黑腔形成动力学过程模拟.

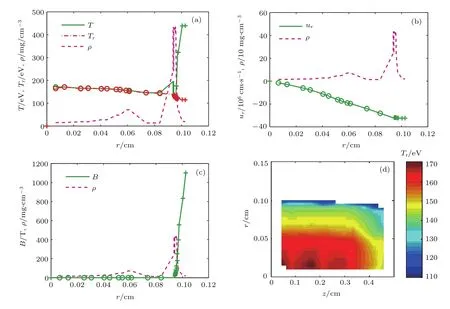
图10 (网刊彩色)152 ns时各时刻参量随空间变化 (a)辐射温度、物质温度和密度分布;(b)速度和密度分布;(c)磁场和密度分布;(d)辐射温度空间分布Fig.10.(color online)The spatial pro fi les of some physical quantities at 152 ns:(a)Radiation,plamsa temperatures,and density pro fi les;(b)velocity and density pro fi les;(c)magnetic fi eld and density pro fi les;(d)spatial distribution of radiation temperature.The part of a line with symbols of circle belongs to foam,and it with symbols of plus belongs to wire-array.

利用新研制的磁场演化方程程序模块,对磁场的扩散和对流演化规律进行了一些研究.发现温度和密度的增大会抑制磁场的扩散;负径向速度梯度的流体(如Z箍缩等离子体的箍缩运动)也会抑制磁场的扩散.当等离子体静止时,磁扩散速度随着时间的增加,迅速减少,然后趋于零,磁场分布变得稳定;当等离子体以恒速箍缩时,磁扩散速度也是电流加载后快速下降,然后趋同于流体运动速度,表明磁场被冻结等离子体中,随流体一起运动;当等离子体以随半径变小而减少的速度做箍缩运动时,磁场的扩散速度略小于运动速度,表明磁场扩散过程被削弱了,出现磁场的再趋肤现象.通过对磁场演化的分析,有助于理解Z箍缩过程中各种因素对磁场演化的影响趋势.

利用MULTI2D-Z程序对8 MA电流水平的丝阵Z箍缩驱动的动态黑腔形成动力学过程进行了模拟,再现了该动态黑腔的形成过程.动态黑腔形成过程的整体特征与国内外的模拟结果基本相似,黑腔辐射温度与相同电流水平下一维CRMHA程序的模拟结果接近,说明了该程序用于动态黑腔形成过程模拟的可靠性.本模拟中发现,在Z箍缩等离子体的高温高密度和对流的共同作用下,磁场主要集中在钨等离子体表面,使丝阵等离子体快速内爆,并撞击泡沫柱;钨主体等离子体的辐射向泡沫柱传播,使泡沫烧蚀而膨胀;丝阵等离子体碰撞泡沫柱,形成很强的物质冲击波和辐射,辐射向泡沫等离子体中传播,形成辐射热波;在泡沫等离子体中辐射热波的传播比物质温度的传输速度快,当辐射热波传播到中心轴后,泡沫中的辐射达到了较好的均匀化(约120 eV),并且除了冲击波附近外,辐射温度和物质温度基本上重合,没有分离现象;此后,随着整体箍缩的进行,泡沫等离子体继续被加速和压缩,其中的辐射温度继续提升,辐射场在轴向方向的均匀性有所增加,但在径向方向的均匀性有所下降.当泡沫柱中嵌套有聚变靶丸时,需要通过程序模拟谨慎、精确地设计丝阵和泡沫柱的尺寸和质量,以便能得到满足聚变点火要求的动态黑腔辐射场时间窗口和空间区域.

动态黑腔形成过程的数值模拟对相关实验的设计和物理过程的理解,以及Z箍缩惯性约束聚变概念设计是非常重要的.今后还需要继续完善和发展MULTI2D-Z程序,改善其辐射模型,评估非结构网格划分对模拟结果的影响.

感谢北京应用物理与计算数学研究所的文武老师、薛创老师、邬吉明研究员和高志明老师以及中国工程物理研究院研究生部的吴福源师兄在研究工作中给予的指导和帮助.感谢中国工程物理研究院聚龙一号(PTS)装置的Z箍缩实验团队对丝阵Z箍缩和动态黑腔实验结果的交流和分享.

[1]Matzen M K 1997 Phys.Plasmas 4 1519

[2]Qiu A C,Kuai B,Wang L P,Wu G,Cong P T 2008 High Power Laser and Particle Beams 20 1761(in Chinese)[邱爱慈,蒯斌,王亮平,吴刚,丛培天2008强激光与粒子束20 1761]

[3]Huang X B,Zhou S T,Dan J K,Ren X D,Wang K L,Zhang S Q,Li J,Xu Q,Cai H C,Duan S C,Ouyang K,Chen G H,Ji C,Wei B,Feng S P,Wang M,Xie W P,Deng J J,Zhou X W,Yang Y 2015 Phys.Plasmas 22 072707

[4]Dan J K,Ren X D,Huang X B,Zhang S Q,Zhou S T,Duan S C,Ouyang K,Cai H C,Wei B,Ji C,He A,Xia M H,Feng S P,Wang M,Xie W P 2013 Acta Phys.Sin.62 245201(in Chinese)[但加坤,任晓东,黄显宾,张思群,周少彤,段书超,欧阳凯,蔡红春,卫兵,计策,何安,夏明鹤,丰树平,王勐,谢卫平2013物理学报62 245201]

[5]Jiang S Q,Ning J M,Chen F X,Ye F,Xue F B,Li L B,Yang J L,Chen J C,Zhou L,Qin Y,Li Z H,Xu R K,Xu Z P 2013 Acta Phys.Sin.62 155203(in Chinese)[蒋树庆,甯家敏,陈法新,叶繁,薛飞彪,李林波,杨建伦,陈进川,周林,秦义,李正宏,徐荣昆,许泽平 2013物理学报62 155203]

[6]Deeney C,Nash T J,Spielman R B,Seaman J F,Chandler G C,Struve K W,Porter J L,Stygar W A,McGum J S,Jobe D O,Gilliland T L,Torres J A,Vargas M F,Ruggles L E,Breeze S,Mock R C,Douglas M R,Fehl D L,McDaniel D H,Matzen M K,Peterson D L,MatuskaW,Roderick N F,MacFarlane J J 1997 Phys.Rev.E 56 5945

[7]Spielman R B,Deeney C,Chandler G A,Douglas M R,Fehl D L,Matzen M K,McDaniel D H,Nash T J,PorterJ L,Sanford T W L,Seaman J F,Stygar W A,Struve K W,Breeze S P,McGurn J S,Torres J A,Zagar D M,Gilliland T L,Jobe D O,McKenney J L,Mock R C,Vargas M,Wangoner T,Peterson D L 1998 Phys.Plasmas 5 2105

[8]Stygar W A,Ives H C,Fehl D L,Fehl D L,Cuneo M E,Mazarakis M G,Bailey J E,Bennett G R,Bliss D E,Chandler G A,Leeper R J,Matzen M K,McDaniel D H,McGurn J S,McKenney J L,Mix L P,Muron D J,Porter J L,Ramirez J S,Ruggles L E,Seamen J F,Simpson W W,Speas C S,Spielman R B,Struve K W 2004 Phys.Rev.E 69 046403

[9]Lebedev S V,Mitchell I H,Aliaga-Rossel R,Bland S N,Chittenden J P,Dangor A E,Haines M G 1998 Phys.Rev.Lett.81 4152

[10]Harvey-Thompson A J,Lebedev SV,Patankar S,Bland S N,Burdiak G,Chittenden J P,Colaitis A,de Grouchy P,Doyle H W,Hall G N,Khoory E,Hohenberger M,Pickworth L,Suzuki-Vidal F,Smith R A,Skidmore J,Suttle L,Swadling G F 2012 Phys.Rev.Lett.108 145002

[11]Swadling G F,Lebedev S V,Harvey-Thompson A J,Rozmus W,Burdiak G,Suttle L,Patankar S,Smith R A,Bennett M,Hall G N,Suzuki-Vidal F,Bland S,Yuan J 2015 Phys.Plasmas 22 072706

[12]Leeper R J,Alberts T E,Asay J R,Baca P M,Baker K L,Breeze S P,Chandler G A,Cook D L,Cooper G W,Deeney C,Derzon M S,Douglas M R,Fehl D L,Gilliland T,Hebron D E,Hurst M J,Jobe D O,Kellogg J W,Lash J S,Lazier S E,Matzen M K,McDaniel D H,McGurn J S,Mehlhorn T A,Moats A R,Mock R C,Muron D J,Nash T J,Olson R E,Porter J L,Quintenz J P,Reyes P V,Ruggles L E,Ruiz C L,Sanford T W L,Schmidlapp F A,Seamen J F,Spielman R B,Stark M A,Struve K W,Stygar W A,Tibbetts-Russell D R,Torres J A,Vargas M,Wagoner T C,Wake fi eld C,Hammer J H,Ryutov D D,Tabak M,Wilks S C,Bowers R L,McLenithan K D,Peterson D L 1999 Nucl.Fusion 39 1283

[13]Ning C,Feng Z X,Xue C 2014 Acta Phys.Sin.63 125208(in Chinese)[宁成,丰志兴,薛创 2014物理学报63 125208]

[14]Bailey J E,Chandler G A,Slutz S A,Bennett G R,Cooper G,Lash J S,Lazier S,Lemke R,Nash T J,Nielsen D S,Moore T C,Ruiz C L,Schroen D G,Smelser R,Torres J,Vese y R A 2002 Phys.Rev.Lett.89 095004

[15]Rochau G A,Bailey J E,Maron Y,Chandler G A,Dunham G S,Fisher D V,Fisher V I,Lemke R W,Mac-Farlane J J,Peterson K J,Schroen D G,Slutz S A,Stambulchik E 2008 Phys.Rev.Lett.100 125004

[16]Ruiz C L,Cooper G W,Slutz S A,Bailey J E,Chandler G A,Nash T J,Mehlhorn T A,Leeper R J,Fehl D,Nelson A J,Franklin J,Ziegler L 2004 Phys.Rev.Lett.93 015001

[17]Zimmerman G B,Kruer W B 1975 Comments Plasma Phys.Control.Fusion 2 51

[18]Slutz S A,Peterson K J,Vesey R A,Lemke R W,Bailey J E,Varnum W,Ruiz C L,Cooper G W,Chandler GA,Rochau G A,Mehlhorn T A 2006 Phys.Plasmas 13 102701

[19]Meng S J,Huang Z C,Ning J M,Hu Q Y,Ye F,Qin Y,Xu Z P,Xu R K 2016 Acta Phys.Sin.65 075201(in Chinese)[蒙世坚,黄展常,甯家敏,胡青元,叶繁,秦义,许泽平,徐荣昆2016物理学报65 075201]

[20]Xiao D L,Sun S K,Xue C,Zhang Y,Ding N 2015 Acta Phys.Sin.64 235203(in Chinese)[肖德龙,孙顺凯,薛创,张扬,丁宁2015物理学报64 235203]

[21]Xiao D L,Ding N,Ye F,Ning J M,Hu Q Y,Chen F X,Qin Y,Xu R K,Li Z H,Sun S K 2014 Phys.Plasmas 21 042704

[22]Ramis R,Ramirez J,Meyer-ter-Vehn J 1988 Comput.Phys.Commun.49 475

[23]Ramis R,Meyer-ter-Vehn J,Ramirez J 2009 Comput.Phys.Commun.180 977

[24]Ramis R,Meyer-ter-Vehn J,Ramirez J 2016 Comput.Phys.Commun.203 226

[25]Liberman M A,De Groot J S,Toor A 2003 Physics of High-Density Z-Pinch Plasmas(Beijing:National Defence Industry Press)(in Chinese)[Liberman M A,De Groot J S,Toor A著(孙承纬译)2003高密度Z箍缩等离子体物理学(北京:国防工业出版社)

[26]Ning C,Yang Z H,Ding N 2003 Acta Phys.Sin.52 415(in Chinese)[宁成,杨震华,丁宁 2003物理学报52 415]

[27]Murakami M,Meyer-ter-Vehn J,Ramis R 1990 J.X-Ray Sci.Technol.2 127

[28]Salamann D 1998 Atom Physics in Hot Plasmas(New York:Oxford University Press)p28

[29]Kemp A J,Meyer-ter-Vehn J 1998 Nucl.Instrum.Meth.A 415 674

[30]More R,Warren K H,Yong D A,Zimmermann G 1988 Phys.Fluids 31 3059

PACS:52.58.Lq,52.59.Qy,52.30.Cv,52.38.PhDOI:10.7498/aps.66.125202

Simulation of forming process of Z-pinch dynamic
hohlraum based on the program MULTI2D-Z∗

Chen Zhong-Wang Ning Cheng†

(Institute of Applied Physics and Computational Mathematics,Beijing 100088,China)

26 December 2016;revised manuscript

12 April 2017)

The radiation hydrodynamics code MULTI-2D,which was developed by Ramis et al.in 2009(2009 Comput.Phys.Commun.180 977)and adopted the single temperature fl uid and unstructured lagrangian mesh,is modi fi ed into a radiation magnetohydrodynamics code MULTI2D-Z by adding the program module of evolution equation of magnetic fi eld,and self-consistently considering the Lorentz force in the module of motion equation and the Ohmic heating in the module of energy equation.The newly developed module for magnetic fi eld was validated to be reliable.The module is used to study the magnetic fi eld di ff usion process,and it is found that the di ff usion is weakened due to the increasing of plasma temperature and density and the fl uid convection,in which there is minus grads of velocity in radial direction.The new code MULTI2D-Z is used to simulate the formation process of dynamic hohlraum driven by tungsten wire-array Z-pinch at an 8 MA current level.The obtained results are that X-ray power and energy are,respectively,∼30 TW and∼300 kJ,radiation temperature in foam is∼120 eV,and the implosion trajectory of wire-array is also obtained.The calculated results reveal that the magnetic fi eld is mainly distributed in the outside of tungsten plasma during the hohlraum formation.The foam expands due to the radiation heating from the shock wave created by the collision between wire-array plasma and the foam.The thermal radiation wave,which is characterized by radiation temperature,spreads towards the central axis faster than the plasma temperature.When the thermal radiation wave spreads to the central axis,the radiation temperature becomes comparatively uniform in space,and is almost equal to the plasma temperature except at the place of the shock wave.These results help the people to better understand the magnetic fi eld di ff usion and convection in Z-pinch,as well as the formation mechanism of dynamic hohlraum driven by wire-array Z-pinch.It is also indicated that the newly developed code MULTI2D-Z can be considered as a new tool for simulating Z-pinch and its applications,such as inertial con fi nement fusion and magnetically accelerated fl yer plates.

Z-pinch,dynamic hohlraum,radiation magnetohydrodynamics,MULTI-2D code

10.7498/aps.66.125202

∗国家自然科学基金(批准号:11675025)和国家自然科学基金重点项目(批准号:11135007)资助的课题.

†通信作者.E-mail:ning_cheng@iapcm.ac.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant No.11675025)and the Key Program of the National Natural Science Foundation of China(Grant No.11135007).

†Corresponding author.E-mail:ning_cheng@iapcm.ac.cn