FeMnP1−xTx(T=Si,Ga,Ge)系列化合物机械性能的第一性原理研究∗
2017-08-07马爽乌仁图雅特古斯武晓霞管鹏飞那日苏
马爽 乌仁图雅 特古斯 武晓霞 管鹏飞 那日苏†
1)(内蒙古师范大学物理与电子信息学院,呼和浩特 010022)
2)(内蒙古科技大学理学院,包头 014010)
3)(北京计算科学研究中心,北京 100193)
FeMnP1−xTx(T=Si,Ga,Ge)系列化合物机械性能的第一性原理研究∗
马爽1)乌仁图雅1)特古斯1)武晓霞2)管鹏飞3)那日苏1)†
1)(内蒙古师范大学物理与电子信息学院,呼和浩特 010022)
2)(内蒙古科技大学理学院,包头 014010)
3)(北京计算科学研究中心,北京 100193)
(2016年12月7日收到;2017年3月21日收到修改稿)
以密度泛函理论为基础,使用投影缀加波方法、VASP程序包研究了FeMnP1−xTx(T=Si,Ga,Ge)化合物的力学性质,结果表明FeMnP1−xGax化合物的晶格参数、弹性常数和电子结构与FeMnP1−xGex化合物比较接近,同时该化合物在力学上稳定,是预期具有较大的磁熵变和高磁热效应的材料.依据Pugh判据,FeMnP0.67T0.33(T=Si,Ga,Ge)化合物具有良好的延展性,三者之中FeMnP0.67Ga0.33韧性最好,FeMnP0.67Si0.33韧性相对较差,说明Ga替代P可改善此类化合物的机械性能.最后从化合物体系电子总态密度随不同掺杂T原子的演化规律解释了自洽计算得到的弹性常数的变化规律.
第一性原理计算,FeMnP1−xTx(T=Si,Ga,Ge)化合物,机械性能
1 引 言
在功能磁性材料领域,一级磁相变的化合物由于其潜在的应用价值引起了广泛的关注,特别是针对非连续相变系统磁卡效应(magnetocaloric e ff ect)的研究[1−3].磁卡效应的应用前景之一就是磁制冷技术,磁制冷技术被看作代替传统蒸汽压缩技术的较好选择,因为其具有环境友好、工作物质是更加紧凑的固体、价格低廉等诸多良好的性能[4,5].近些年来的研究发现了许多具有巨大磁卡效应和磁熵变的材料,例如FeRh[6]、Gd5Si2Ge2[7]、La(Fe,Si)13基化合物及其氢化物[8−10],Fe2MnGa等Heusler合金[11,12].这些材料的共同特点是结构相变与磁相变交织在一起,所以具有巨磁卡效应的同时,通常也伴随着由结构相变引起的巨弹性热效应,也就是外场驱动的多卡效应.经典的热力学认为,物质的任何有序度改变,往往伴随着熵的改变,进而伴随热效应.除外加磁场产生磁热效应之外,压力也可以产生压热效应.但是,一般情况下无结构相变的固态材料的压热效应都很小,较少引起人们关注.
基于六角相Fe2P的铁锰基系列化合物,在拥有显著磁卡效应的同时,还有着低成本、无毒环保、可在室温下应用的良好性能[13−16].到目前为止,对FeMnPT(T=As,Ge,Si)化合物[17−20]、掺杂B元素的FeMnPSi化合物[21]的研究表明,这些化合物都存在较大的磁熵变和磁卡效应.作为磁制冷工质材料,在反复的热加载和磁化过程中,FeMnP1−xTx化合物应具有良好的机械性能和力学稳定性.但是到目前为止,有关此类材料的机械性能、韧脆性的研究相对较少[4].实验中发现,多晶FeMnPSi化合物块体样品在后期处理过程中会出现碎裂现象,破坏样品的磁热性能,大大降低了样品的磁热效率.样品的碎裂可能是由于Fe2P型化合物样品经历顺磁到铁磁相变时伴随的自发磁弹性耦合效应[15,16],它使多晶材料内部产生较大应力.为此,优化或改善FeMnPT化合物的机械性能变得尤为重要.合金化是改善单相材料的力学性能的有力手段,为此我们研究组理论研究了Ga替代P的FeMnP1−xGax化合物,发现该化合物具有稳定的六方相,且在铁磁-顺磁相变过程中呈现较大磁熵变和相变潜热,而其力学性质尚待进一步研究.本文运用密度泛函理论(DFT)研究Fe2P型FeMnP1−xTx(T=Si,Ga,Ge)化合物的力学性质与机械性能.
2 模型与计算细节
2.1 计算模型
六角相的Fe2P空间群是P¯62m,原胞中有六个Fe原子和三个P原子.其中三个Fe原子属于Fe(I),在3f(0.257,0,0)晶位;三个Fe原子属于Fe(II),在3g(0.591,0,0.5)晶位;两个P原子属于P(I),在2c(0.333,0.667,0)晶位,一个P原子属于P(II),在1b(0,0,0.5)晶位.Fe(I)与近邻的四个P原子组成四面体,3f位置也称为四面体晶位;Fe(II)与近邻的五个P原子组成棱锥体,3g位置也称为棱锥体晶位.图1中标注了晶格的具体占位.
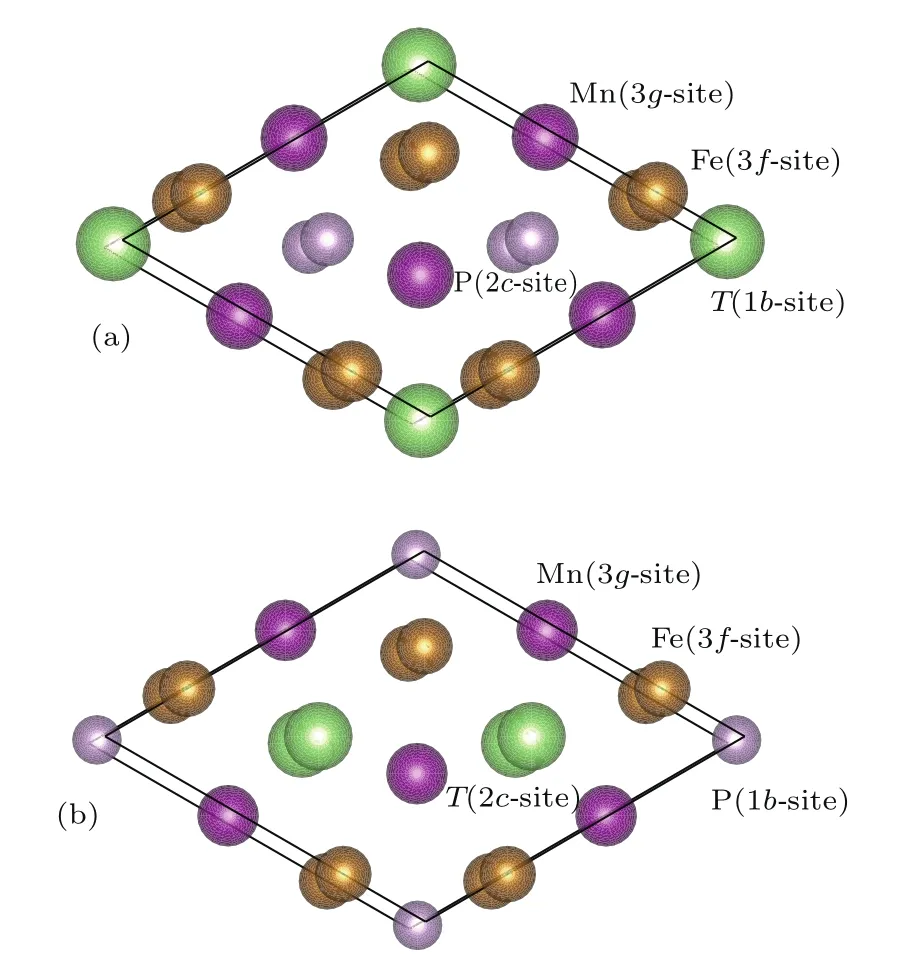
图1 (网刊彩色)FeMnP1−xTx(T=Si,Ga,Ge)化合物的原胞模型 (a)x=0.33;(b)x=0.67Fig.1.(color online)Cell structures of FeMnP1−xTx(T=Si,Ga,Ge)compounds:(a)x=0.33;(b)x=0.67.
FeMnP1−xTx(T=Si,Ga,Ge)化合物的晶体结构建立在六角相Fe2P的基础上,同时参考FeMnP1−xSix[18−20],FeMnP1−xGex[22]的晶体结构,令Fe原子占据3f晶位,Mn原子占据3g晶位,同时考虑到不同掺杂浓度以及T原子占位对FeMnP1−xTx(T=Si,Ga,Ge)化合物力学性能的影响,我们选掺杂浓度为x=0.33(图1(a))和x=0.67(图1(b)).x=0.33时,T原子占1b晶位;x=0.67时,T原子占据2c晶位,如图1所示.
2.2 机械性能的计算
为了研究FeMnP1−xTx(T=Si,Ga,Ge)化合物的机械性能,计算了体系的弹性常数.六角相晶系需要C11,C12,C13,C33和C44五个独立的弹性常数描述任意形变下的能量变化[23]:

其中,ei(i=1,···,6)为应变张量;O(e3)为略去项;C11,C12可组合为弹性常数C66=(C11−C12)/2.在特定体积下的FeMnP1−xTx(T=Si,Ga,Ge)取不同c/a进行充分弛豫,再对不同体积应用Murnaghan方程对物态方程拟合[24],得到其平衡体积、体模量B和无量纲量R.B和R又可以表示为弹性常数的组合形式B=[C33(C11+C12)−2(C13)2]/Cs,R=(C33−C11−C12+C13)/Cs.弹性常数Cs是由体积保持不变的形变得到,它表示为Cs=C11+C12+2C33−4C13,弹性常数C66和C44分别由体积保持不变的正交形变和单斜拉伸形变得到[25].用计算出的B,R,Cs,C66,求出C11,C12,C13,C33,这些数据需满足六角晶系力学稳定条件,
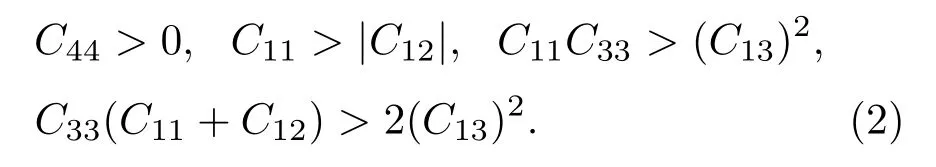
此外,对于多晶材料,结合Voigt和Reuss模型得到剪切模量和体弹性模量分别为

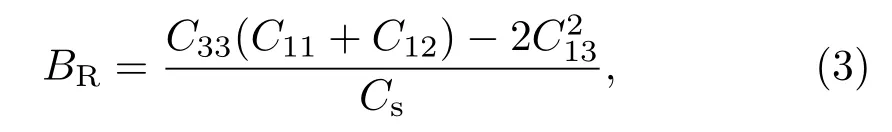
其中,c2=C33(C11+C12)−2(C13)2.
弹性的各向异性用AVR表示,AVR=(GV−GR)/(GV+GR),按照Hill建议取剪切模量和体弹性模量的平均值作为参考,即GH=(GV+GR)/2,BH=(BV+BR)/2.
杨氏模量E,泊松比v为

2.3 计算设置
本文计算的晶格弛豫以及机械性能是以DFT[26,27]为基础,投影缀加波方法[28]、VASP(Vienna ab initio simulation package)[29]为工具.使用广义梯度近似下的Perdew-Burke-Ernzerhof交换关联势进行计算[30].平面波基函数截断能设置为530 eV,电子弛豫自洽计算的能量收敛标准设置为10−5eV·atom−1,原子之间相互作用力收敛判据设置为0.01 eV·Å−1.布里渊区积分的k点使用Monkhorst-Pack特殊撒点方式[31],k点网格点的设置为11×11×17.在此基础之上,对不同体积下的FeMnP1−xTx(T=Si,Ga,Ge)化合物取不同c/a充分弛豫,得到优化结构,应用Murnaghan方程对物态方程进行拟合,得到体系的平衡体积和体模量B,最后计算弹性常数时形变应变量设置为δ=0.00—0.05.
3 计算结果与讨论
3.1 FeMnP1−xTx(T=Si,Ga,Ge)化合物的结构
表1列出了FeMnP1−xTx(T=Si,Ga,Ge)化合物的晶格常数、能量、磁矩和Fe,Mn原子占位的数值,同时与FeMnP1−xTx(T=Si,Ge)的理论和实验上的数值对比,以验证计算结果的可靠性.通过对比可看出,FeMnP1−xTx(T=Si,Ga,Ge)化合物均具有较大的磁矩,FeMnP1−xGax的原胞磁矩均大于FeMnP1−xSix和FeMnP1−xGex的磁矩,说明FeMnP1−xGax化合物可能具有较大的磁熵变和高磁热效应[18−20].此外,通过对比FeMnP1−xGax和FeMnP1−xGex,两者各项参数的值接近,可见由于Ga原子和Ge原子的半径相似,各项性能也比较接近.
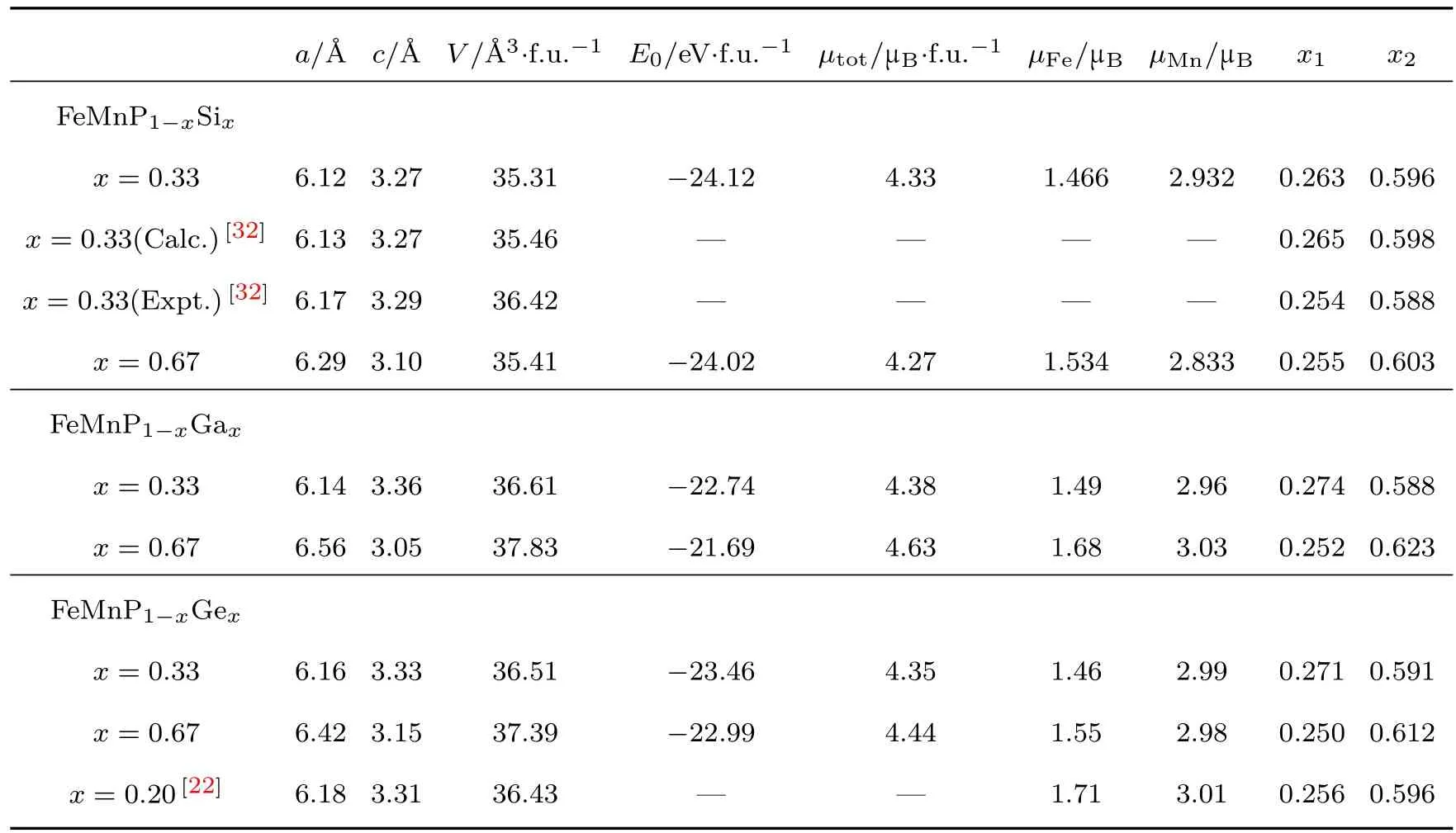
表1 FeMnP1−xTx(T=Si,Ga,Ge)化合物的晶格常数、能量、磁矩和部分原子的占位Table 1. Lattice parameters,energy,magnetic moments,and fractional atomic positions of the FeMnP1−xTx(T=Si,Ga,Ge)compounds.
3.2 FeMnP1−xTx(T=Si,Ga,Ge)化合物的力学性质
由于磁热材料在反复的磁热循环中工作,所以具备良好的机械稳定性是十分必要的.表2和表3列出了两个组分FeMnP1−xTx(T=Si,Ga,Ge)化合物的弹性常数,用来判断化合物的机械性能与韧脆性.
表2中本文计算出的FeMnP0.67Si0.33弹性常数的值与其他理论计算得出的结果接近.首先,两种组分的FeMnP1−xTx(T=Si,Ga,Ge)化合物的弹性常数均满足六角晶系力学稳定条件,即化合物在力学上是稳定的.其次,对于两种组分FeMnP1−xTx(T=Ga,Ge)化合物Cs的数值差异较大,可能是由于其结构中存在很强的磁有序效应.通过对比FeMnP1−xGax化合物和FeMnP1−xGex化合物的弹性常数,除了C12之外,其余弹性常数随掺杂浓度的增加而发生改变的趋势相同,主要原因可能是晶格参数、体模量的变化以及弹性的各向异性导致.最后,当C44大于C12时,体系显示着类共价键合特征,反之亦然.对于两种组分FeMnP1−xTx(T=Si,Ga,Ge)化合物都有着明显的类共价键特征.
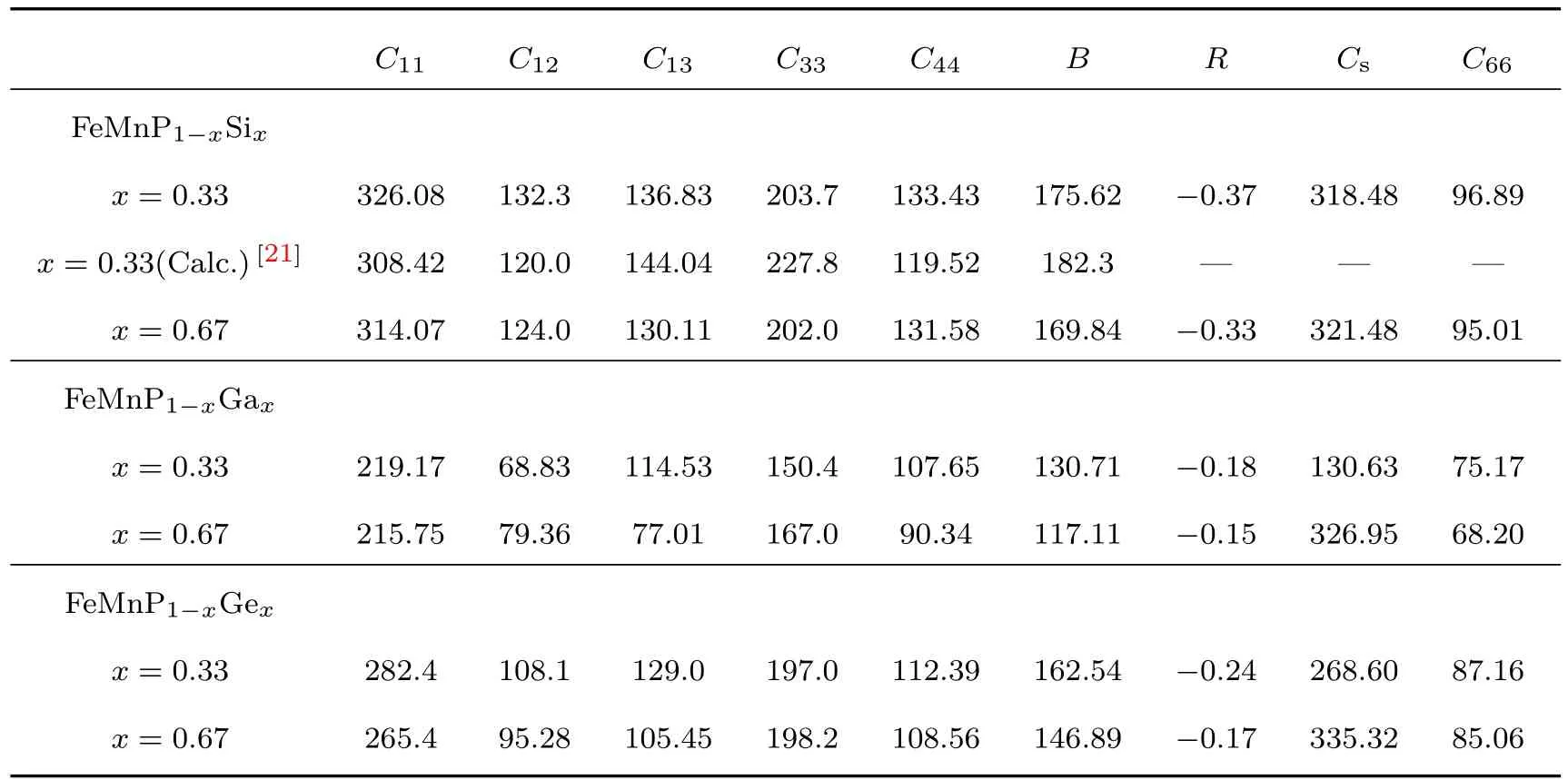
表2 FeMnP1−xTx(T=Si,Ga,Ge)化合物的弹性常数(单位:GPa)Table 2.Elastic constants of FeMnP1−xTx(T=Si,Ga,Ge)compounds(unit:GPa).

表3 FeMnP1−xTx(T=Si,Ga,Ge)化合物的弹性模量(单位:GPa)Table 3.Elastic moduli of FeMnP1−xTx(T=Si,Ga,Ge)compounds(unit:GPa).
材料的韧脆性主要基于理论上的断裂强度和单晶剪切模量,Pugh[33]总结了大量实验数据,发现材料的韧脆性与体弹性模量BH和剪切模量GH的比值有关,通常来说,韧性材料BH/GH的值大于1.75.而脆性材料BH/GH的值小于1.75,这一判据在现代计算材料科学中被广泛应用来判定材料的韧脆性[34,35].泊松比v可以反映晶体对剪切的稳定性,对于各向同性的多晶材料,由体弹性模量和剪切模量可确定其泊松比v,因此Pugh判据规定了泊松比v也可判别材料的韧脆性,韧性材料泊松比v的值大于0.26,而脆性材料泊松比v的值小于0.26.
结合材料韧脆性的判据,对表3数值进行分析.在机械性能、韧脆性方面,FeMnP0.67T0.33(T=Si,Ga,Ge)化合物呈现韧性,因为泊松比v(Ga)>v(Ge)>v(Si),所以FeMnP0.67Ga0.33化合物的韧性是最好的,FeMnP0.67Si0.33化合物的韧性是相对较差的;而FeMnP0.33T0.67(T=Si,Ga,Ge)化合物处于韧性和脆性的临界状态,由于对机械性能的研究是在Si,Ga,Ge原子仅占在1b或2c晶位的两个极端情况下,因此我们推测实际上原子占位的无序性可能会增加x=0.67组分化合物的延展性.
3.3 FeMnP1−xTx(T=Si,Ga,Ge)化合物电子结构

图2 (网刊彩色)FeMnP1−xTx(T=Si,Ga,Ge)化合物的态密度 (a),(c),(e)x=0.33;(b),(d),(f)x=0.67Fig.2.(color online)Density of states of FeMnP1−xTx(T=Si,Ga,Ge)compounds:(a),(c),(e)x=0.33;(b),(d),(f)x=0.67.
为了进一步探究机械性能,深入了解弹性常数与电子结构的关联,对FeMnP1−xTx(T=Si,Ga,Ge)化合物的电子结构进行了分析讨论,图2(a)和图2(b)是两种组分的FeMnP1−xTx(T=Si,Ga,Ge;x=0.33,0.67)化合物基态的电子态密度,图中态密度的正负值代表多数自旋子带和少数自旋子带的态密度,自旋向上和自旋向下电子的不对称分布导致体系呈现铁磁性.分析可知,两种组分FeMnP1−xTx(T=Si,Ga,Ge)化合物中Fe,Mn原子之间存在较强的类共价键合,态密度的峰主要来源于Fe,Mn原子3d轨道电子的贡献,两者的d轨道上的电子互相重叠,进而导致电子轨道存在很强的杂化.FeMnP1−xGax和FeMnP1−xGex化合物态密度的整体形状相似,由于Ga原子比Ge原子少一个d电子,所以态密度上的费米能级要移向较低的状态,二者电子结构的相近导致它们各项性能也十分接近.
图2(c)和图2(d)给出了FeMnP1−xSix化合物在单斜形变 (δm=0.05)、正交形变(δo=0.05)以及无形变 (δ=0.00)状态下的电子态密度,由正则能带理论可知[36,37],晶格形变时对应能量的变化∆E由动能∆Eki(其中能带填充能量∆EB起主要作用)和静电能∆Ees组成,由于不同元素的掺杂对静电能因形变而产生的变化影响不大,所以能带填充能量∆EB的变化对∆E的变化起主要作用.在相同形变下,∆EB的正负决定∆E的大小.从图2(c)和图2(d)可以看出,两种组分FeMnP1−xSix化合物形变后基本保持了原有的稳定性和磁性,说明晶格的形变对于体系的相对稳定性影响较弱.在图中可看出单斜形变δm(∆E ∼2V C44δ2m)下的态密度向着高能方向移动,体系的EB增加(∆EB>0);而正交形变δo(∆E∼2V C66δ2m)下的态密度向着低能方向移动,体系的EB减小(∆EB<0).因此体系具有较大的C44和较小的C66,即C66 根据力定理(force theorem)[37,38],当费米面穿过总态密度上的赝能隙时,费米面处的态密度对形变并不敏感,因此体系较为稳定,具有相对较大的弹性常数.反之费米面穿过态密度峰,则体系弹性常数较小.从图2(e)和图2(f)可以看出,两种组分FeMnP1−xTx化合物在费米面处的总态密度(TDOS)值DFermi(Si) 本文通过DFT研究了FeMnP1−xTx(T=Si,Ga,Ge)化合物的力学性质以及机械性能.分析计算结果如下:1)FeMnP1−xGax和FeMnP1−xGex化合物在晶格常数、能量、磁矩、电子结构等方面十分接近,同时在力学上稳定;2)在机械性能方面,用材料韧脆性的判据对FeMnP1−xTx(T=Si,Ga,Ge)化合物进行判别,FeMnP0.67T0.33(T=Si,Ga,Ge)化合物均呈现韧性,其中FeMnP0.67Ga0.33的韧性最好,FeMnP0.67Si0.33的韧性相对稍差;以上结果说明可通过Ga替代P原子改善FeMnP1−xTx化合物的机械性能;3)FeMnP0.33T0.67(T=Si,Ga,Ge)化合物处在韧性和脆性的临界状态,但我们研究的原子T仅占在1b或2c晶位的特殊情况,原子占位的无序性可能会改善高T组分化合物的韧性;4)弹性常数随不同掺杂原子的变化规律可通过电子结构分析和力定理解释,说明对此类复杂化合物系统力定理依然成立.关于原子占位的无序性对FeMnP1−xTx(T=Si,Ga,Ge)化合物机械性能的影响,有待在以后工作中进一步讨论. [1]Gschneidner Jr K A,Pecharsky V K,Tsokol A O 2005 Rep.Prog.Phys.68 1479 [2]Smith A,Bahl C R,Bjork R,Engelbrecht K,Nielsen K K,Pryds N 2012 Adv.Energy Mater.2 1288 [3]Yibole H,Guillou F,Caron L,Jimenez E,de Groot F M F,Roy P,de Groot R,Bruck E 2015 Phys.Rev.B 91 014429 [4]Bruck E,Tegus O,Thanh D T C,Buschow K H J 2007 J.Magn.Magn.Mater.310 2793 [5]Li G J,Li W,Stephan S,Li X Q,Delczeg-Czirjak E K,Yaroslav O K,Olle E,Börje J,Levente V 2014 Appl.Phys.Lett.105 262405 [6]Annaorazov M P,Nikitin S A,Tyurin A L,Asatryan K A,Dovletvo A K 1996 J.Appl.Phys.79 1689 [7]Pecharsky V K,Gschneidner Jr K A 1997 Phys.Rev.Lett.78 4494 [8]Fujita A,Fujieda S,Hasegawa Y,Fukamichi K 2003 Phys.Rev.B 67 104416 [9]Hai X Y,Mayer C,Colin C V,Miraglia S 2016 J.Magn.Magn.Mater.400 344 [10]Li S P,Huang R J,Zhao Y Q,Wang W,Li L F 2015 Phys.Chem.Chem.Phys.17 30999 [11]Kudryavtsev Y V,Uvarov N V,Iermolenko V N,Glavatskyy I N,Dubowik J 2012 Acta Mater.60 4780 [12]Tang X D,Wang W H,Zhu W,Liu E K,Wu G H,Meng F B,Liu H Y,Luo H Z 2010 Appl.Phys.Lett.97 242513 [13]Moya X,Kar-Narayan S,Mathur N D 2014 Nat.Mater.13 439 [14]Guillou F,Porcari G,Yibole H,van Dijk N H,Bruck E 2014 Adv.Mater.26 2671 [15]Miao X F,Caron L,Roy P,Dung N H,Zhang L,Kockelmann A,de Groot R A,van Dijk N H,Bruck E 2014 Phys.Rev.B 89 174429 [16]Gercsi Z,Delczeg-Czirjak E K,Vitos L,Wills A S,Daoud A A,Sandeman K G 2013 Phys.Rev.B 88 024417 [17]Tegus O,Bruck E,Buschow K H J,de Boer F R 2002 Nature 415 150 [18]Guillou F,Ollefs K,Wilhelm F,Rogalev A 2015 Phys.Rev.B 92 224427 [19]Hoglin V,Andersson M S,Sarkar T,Nordblad P,Sahlberg M 2015 J.Magn.Magn.Mater.374 455 [20]Delczeg-Czirjak E K,Pereiro M,Bergqvist L,Kvashnin Y O,Marco I D,Li G J,Vitos L,Eriksson O 2014 Phys.Rev.B 90 214436 [21]Roy P,Torun E,de Groot R A 2016 Phys.Rev.B 93 094110 [22]Liu D,Yue M,Zhang J X,Mcqueen T M,Lynn J W,Wang X L,Chen Y,Li J Y,Cava R J,Liu X B,Altounian Z,Huang Q 2009 Phys.Rev.B 79 014435 [23]Vitos L 2007 Computational Quantum Mechanics for Materials Engineers:The EMTO Method and Applications(London:Springer-Verlag)pp107–113 [24]Murnaghan F D 1994 The Compressibility of Media Under Extreme Pressures(USA:Proc Natl Acad Sci)pp244–247 [25]Grimvall G 1999 Thermophysical Properties of Materials(The Netherlands:Elsevier Science B V)pp27–40 [26]Ernzerhof M,Scuseria G E 2000 Theor.Chem.Acc.103 259 [27]Kohn W,Sham L J 1965 Phys.Rev.140 1133 [28]Blöchl P E 1994 Phys.Rev.B 50 17953 [29]Kresse G,Hanfner J 1993 Phys.Rev.B 47 558 [30]Perdew J P,Burke K,Ernzerhof M 1996 Phys.Rev.Lett.77 3865 [31]Monkhorst H J,Pack J D 1976 Phys.Rev.B 13 5188 [32]Roy P,Brück E,de Groot R A 2016 Phys.Rev.B 93 165101 [33]Pugh S F 1954 Relations between the Elastic Moduli and the Plastic Properties of Polycrystalline Pure Metals(London:Philosophical Magazine)pp823–843 [34]Kwasniak P,Muzyk M,Garbacz H,Kurzydlowski K J 2014 Mater.Sci.Eng.A 590 74 [35]Counts W A,Friak M,Raabe D,Neugebauer J 2009 Acta Mater.57 69 [36]Mackintosh A R,Andersen O K 1980 Electrons at the Fermi Surface(England:Cambridge University Press)pp149–224 [37]Skriver H L 1985 Phys.Rev.B 31 1909 [38]Zhang H L,Punkkinen M P J,Johansson B,Hertzman S,Vitos L 2010 Phys.Rev.B 81 184105 PACS:63.20.dk,75.30.Sg,62.20.–xDOI:10.7498/aps.66.126301 First principles study of mechanical properties of FeMnP1−xTx(T=Si,Ga,Ge)compounds∗ Ma Shuang1)Wu Ren-Tu-Ya1)O Tegus1)Wu Xiao-Xia2)Guan Peng-Fei3)Bai Narsu1)† 1)(College of Physical and Electronic Information,Inner Mongolia Normal University,Hohhot 010022,China) 7 December 2016;revised manuscript 21 March 2017) Magnetic refrigeration technology is considered as a better alternative to traditional steam compression scheme,since it has many advantages such as environment friendly characteristic,more compact solid refrigerant,low cost,etc.The mechanical stability is of essential importance for serving as magnetic refrigerant materials which work under repeatedly thermal and magnetic cycles.Recent experiment reveals that the polycrystalline FeMnP1−xSixcompounds are brittle,and even fracture of samples during post heat treatment is observed.Therefore,the improvement of the ductility of Fe2P-Type FeMn-based magnetocaloric materials becomes an important issue in practical application.So far,there are few studies of the mechanical properties of these compounds.Alloying is an e ff ective method to improve the mechanical properties of single phase materials,and Ga or Ge could be a better choice to replace the Si element.In this paper,we study the mechanical properties of giant magnetocaloric FeMnP1−xTx(T=Si,Ga,Ge)compounds by the projector augmented wave method as implemented in VASP(Vienna ab initio simulation package)in the framework of density functional theory.It is found that the lattice parameter,total energy,magnetic moment,elastic constant and the electronic structure of FeMnP1−xGaxcompounds are similar to those of FeMnP1−xGexcompounds,therefore,it is believed that the FeMnP1−xGaxcompounds are candidate refrigerant for room temperature magnetic refrigeration.The relatively large single crystalline elastic constants of FeMnP1−xTx(T=Si,Ga,Ge)compounds show that this family of compounds is mechanically stable.This ensures the long-term applicability of FeMnP1−xTxcompounds in magnetic refrigeration facilities.For polycrystalline compounds,we calculate their shear moduli and bulk moduli by Hill averaging scheme.And according to Pugh criterion,the ductility or brittleness characteristics of FeMnP1−xTx(T=Si,Ga,Ge)compounds are discussed.All the FeMnP0.67T0.33(T=Si,Ga,Ge)compounds are ductile,among them,FeMnP0.67Ga0.33compound shows the best ductility,whereas the ductility of FeMnP0.67Si0.33compound is the weakest.This result proves that substituting P with Ga could improve the ductility of this class of compound.The mechanical properties of polycrystalline FeMnP0.33T0.67compounds are close to the ductile/brittle critical point.For FeMnP0.33T0.67compounds,the T atoms just occupy the 2c sites of metalloid atom in Fe2P-type structure,therefore it is expected that the occupation disorders of P and T atoms at high T concentration could improve the ductility of the compounds according to the result of FeMnP0.67Ga0.33compound.Finally,the self-consistent elastic constants of di ff erent compounds are understood from the calculated electronic density of states and force theorem. fi rst-principles calculation,FeMnP1−xTx(T=Si,Ga,Ge)compounds,mechanical properties 10.7498/aps.66.126301 ∗国家自然科学基金(批准号:11464037)和内蒙古自然科学基金(批准号:2016MS0113)资助的课题. †通信作者.E-mail:nars@imnu.edu.cn ©2017中国物理学会Chinese Physical Society http://wulixb.iphy.ac.cn *Project supported by the National Natural Science Foundation of China(Grant No.11464037)and the Natural Science Foundation of Inner Mongolia,China(Grant No.2016MS0113). †Corresponding author.E-mail:nars@imnu.edu.cn4 结 论
2)(College of Science,Inner Mongolia University of Science and Technology,Baotou 014010,China)
3)(Beijing Computational Science Research Center(CSRC),China Academy of Engineering Physics,Beijing 100193,China)
