环形光束锥形衍射出射光场偏振特性及光场调控∗
2017-08-07杜闯贾大功张红霞刘铁根张以谟
杜闯 贾大功 张红霞 刘铁根 张以谟
(天津大学精密仪器与光电子工程学院,光电信息科学与技术教育部重点实验室,天津 300072)
环形光束锥形衍射出射光场偏振特性及光场调控∗
杜闯 贾大功†张红霞 刘铁根 张以谟
(天津大学精密仪器与光电子工程学院,光电信息科学与技术教育部重点实验室,天津 300072)
(2017年1月8日收到;2017年3月24日收到修改稿)
环形光束的锥形衍射效应对于微粒的操控具有重要的应用价值.本文建立了环状高斯光束的锥形衍射模型,并基于Berry理论给出了线偏振态下环形光束锥形衍射出射光场的计算公式.理论仿真了环状光锥形衍射出射光场的偏振特性,得出环光锥形衍射出射光场的内、外亮环具有相互正交的偏振分布特性.搭建了线偏振态下环状高斯光锥形衍射的实验系统,实验验证了出射光场的偏振特性.针对环形光束锥形衍射出射光场具备的偏振特性,设计了一种组合偏振片,理论和实验研究了该组合偏振片对环光锥形衍射出射光场的调控.结果表明,随着组合偏振片方位角的变化,锥形衍射出射光场的内、外环强度发生周期性的变化.
双轴晶体,锥形衍射,环状高斯光束,组合偏振片
1 引 言
双轴晶体的锥形折射效应是指当一束光沿着双轴晶体的一个光轴方向入射时会发生特殊的折射现象,光束的传播轨迹呈圆锥形[1−4].Hamilton于1832年预言了双轴晶体锥形折射现象,早期相关理论解释都是以Fresnel波面为基础进行展开,但是这些理论只能给出了定性的描述,甚至有些只是理论假设[5−7].Portigal和Burstein[8]于1969年最早尝试定量描述锥形折射现象,分析了双轴晶体光轴附近的光线传播理论.随后Berry[9]利用傍轴光学近似思想,完善并简化了锥形折射的衍射理论,给出了锥形折射光的解析公式,故又称锥形折射为锥形衍射.上述锥形衍射理论的发展为研究环形光束的锥形衍射现象奠定了理论基础.
随着激光技术的发展,双轴晶体锥形衍射凭借其独特的光场调控能力再度引起了人们的关注,如利用锥形衍射产生平顶型超高斯光束[10]、实现涡旋光束的产生与消除[11]等.研究过程中发现由于入射光束形态不同,其锥形衍射调控结果不同,因此不同形态入射光的锥形衍射出射光场的研究成为该领域的重要研究方向之一,如白光的锥形衍射研究[12]、径向偏振光和角向偏振光的锥形衍射研究[13]、拉盖尔-高斯光束的锥形衍射研究[14]、扇形光的锥形衍射研究[15]等.环形光束作为光镊技术的重要调控光场[16,17],对微粒操控具有重要意义,因此本文对环形光的锥形衍射效应进行研究,以期得到最佳的微粒操控光场.偏振态作为光场的基本特性之一,对光场的调控有着直接的影响[18],而且锥形衍射光场的独特偏振特性也具有重要的应用价值,如O’Dwyer等[19]提出了利用偏振光锥形衍射出射光场的缺陷环进行微球粒子和白血球细胞的捕捉和定位;Peinad等[20]基于锥形衍射出射光场的偏振特性设计了一种新型的偏振计装置,能够高效判别光束的偏振态;Turpin等[21]利用锥形衍射出射光场的偏振特性实现了空间光通信中的偏振复用与解复用.因此,本文给出了环状高斯光束的锥形衍射理论模型和偏振光入射时的光场强度公式,分析了环状光锥形衍射出射光场的偏振特性,并设计一种特殊的组合偏振片实现了对环光锥形衍射出射光场的调控.
2 环状光束的锥形衍射效应及其偏振特性
2.1 环光锥形衍射理论
基于Tovar[22]提出的平顶多高斯光束模型,我们给出了一种环状高斯光束的模型.在柱坐标系中,光束束腰z=0时的环状高斯光光场可以表示为
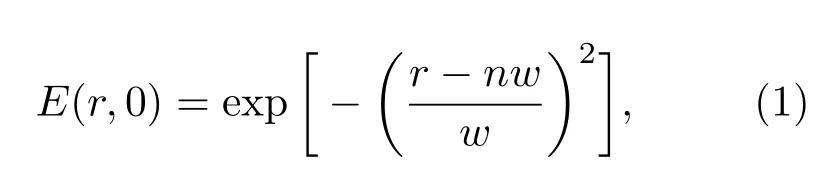
式中,w为高斯光束的腰斑半径,n(n=0,1,2,···)表示环状高斯光束的阶次.为了方便讨论,这里暂时忽略(1)式中的振幅常数因子.当n=0时,(1)式为基模高斯光表达式;当n>0时,(1)式则为环状高斯光束计算公式.本文就是以环形高斯光束作为入射光研究环光锥形衍射出射光场的偏振特性.
对电场矢量为D0的入射光,沿光轴入射到晶体后,晶体后端面出射光场为

式中:J0为零阶贝塞尔函数,a(κ)是入射光的傅里叶变换,各参量具有下式关系:
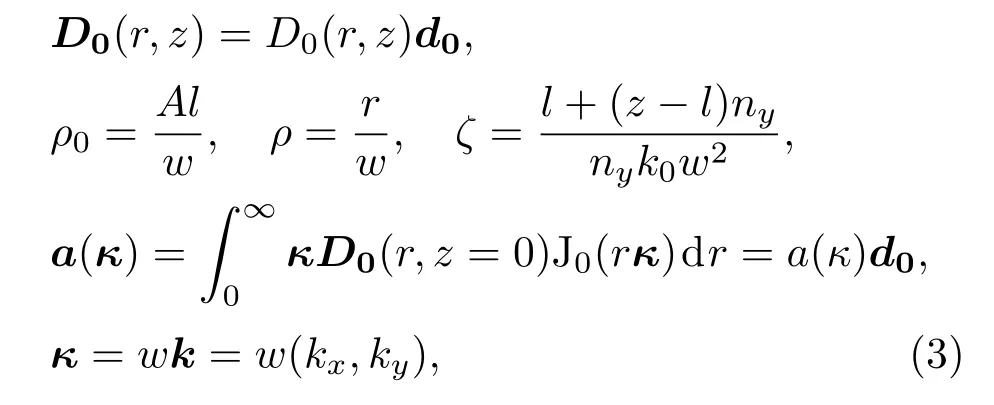
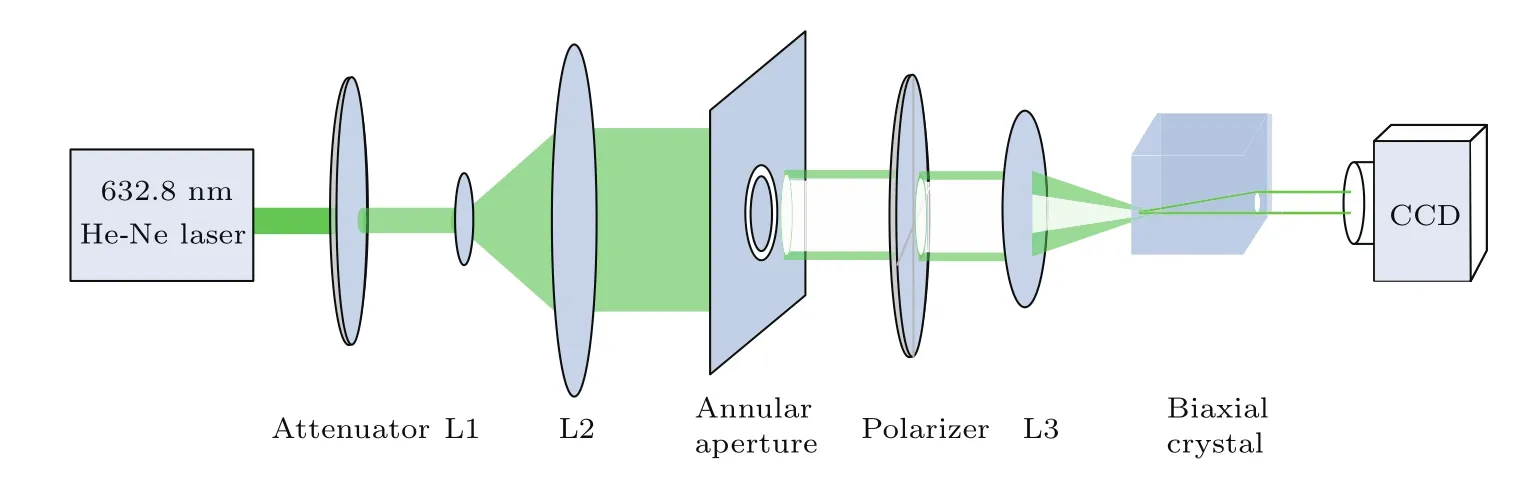
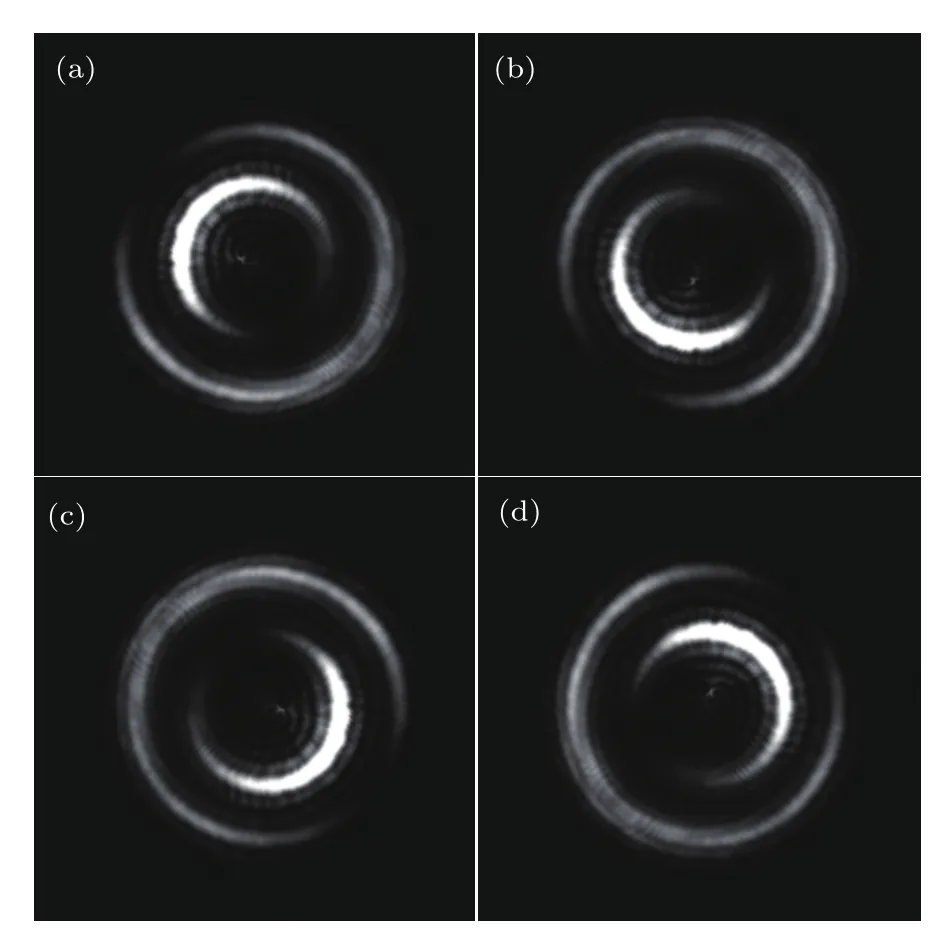
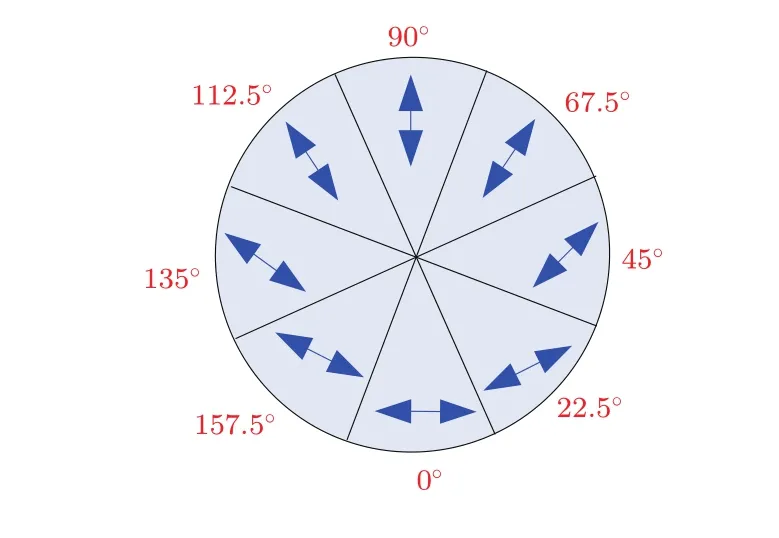
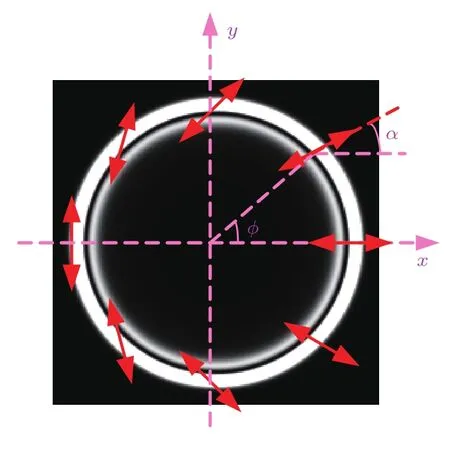
其中,d0表示入射光的偏振态,l为晶体的长度,w是入射光束的束腰半径,r和z为柱面极坐标,z轴的起点是入射光的束腰位置;ρ和ζ为对应于r和z的两个无量纲参数,分别代表锥形衍射出射光的径向和轴向传播位置,ζ轴起点为入射光束腰经过长l的晶体所成等效像的位置(也称该位置为焦像面),焦像面处的锥形衍射出射光场是最清晰的;ρ0参量表示晶体出射面处的锥形衍射光场半径与入射光腰斑半径的比值,ρ0的大小决定着锥形衍射出射光场的细锐程度;A是直角锥的半顶角,假设晶体的主轴折射率分别为nx,ny,nz,并且nx 由(1)式可知,环状高斯光的傅里叶变换为 将(5)式代入到(2)式可得环状高斯光的锥形衍射光场为 其中,I0,Ik,B0,B1分别为如下形式: 通过(7)式可以知道,锥形衍射出射光场由B0和B1两个分量构成,其中B0分量是包含零阶贝塞尔函数的积分式,B1分量是包含一阶贝塞尔函数的积分式. 2.2 环光锥形衍射光场的偏振特性 由于锥形衍射出射光场的偏振分布主要由入射光的形态决定,但是出射光场的光强会受到入射光偏振态的影响[24].按照上述思想,非偏振光束的锥形衍射出射光场经过α角的线偏振片后的光强分布,与偏振方向α角的线偏振光的锥形衍射出射光场特性是一样的.因此,为了分析环形光束锥形衍射出射光场的偏振特性,我们以具有线偏振台的环形光作为入射光束.当入射光为α角的线偏振光时,(6)式中的偏振矩阵可以表示为:则线偏振的环形光束锥形衍射出射光强为 图1 (网刊彩色)线偏振的环状高斯光锥形衍射出射光场(ρ0=40) (a)α=0◦;(b)α=22.5◦;(c)α=45◦;(d)α =67.5◦;(e)α =90◦;(f)α =122.5◦;(g)α =135◦;(h)α =157.5◦;(i)偏振分布示意图Fig.1.(color online)The conical di ff raction patterns with linearly polarized annular Gaussian beam(ρ0=40):(a) α =0◦;(b) α =22.5◦;(c) α =45◦;(d) α =67.5◦;(e) α =90◦;(f) α =122.5◦;(g)α =135◦;(h)α =157.5◦;(i)the diagram of polarization state. 根据(8)式可以理论计算不同偏振方向的线偏振环状高斯光的锥形衍射出射光在焦相面上的光场分布,其结果如图1所示.图1(a)—(h)分别表示偏振方向为0◦,22.5◦,45◦,67.5◦,90◦,122.5◦,135◦和157.5◦的线偏振环状高斯光束的锥形衍射出射光场分布,计算时使用的环状高斯光束阶次为20(n=20),ρ0=40.由图1(a)可知,当入射线偏光偏振方向为0◦时,锥形衍射光场中外环在90◦的方位角处光强为零,而内环却在270◦的方位角处光强为零,因此可以得出,内环270◦方位角和外环90◦方位角处的偏振态均与入射线偏振光正交,为竖直偏振;由图1(e)可知,当入射线偏光偏振方向为90◦时,锥形衍射出射光场的外环在270◦的方位角处光强为零,而内环却在90◦的方位角处光强为零,因此可以得出内环90◦方位角和外环270◦方位角处的偏振态均与入射线偏振光正交,为水平偏振.同理,由图1(b)和(f)、图1(c)和(g)、图1(d)和(h)分别可以得出锥形衍射光内、外环在135◦和315◦,0◦和180◦,45◦和225◦方位角处的偏振态. 综合上述计算结果可知,环状光束锥形衍射出射光场内、外环具有相互正交的偏振分布,如图1(i)所示,其中蓝色箭头和红色箭头分别表示锥形衍射出射光场内环和外环上各点处的偏振方向.图2为高斯光束的锥形衍射出射光场偏振分布[10],红色箭头表示环上各点处的偏振方向.由图1(i)和图2可知,环形光和高斯光的锥形衍射出射光场在焦像面上的光强图均为双亮环结构.不同的是,环形光锥形衍射出射光场内外环偏振态相互正交,而高斯光锥形衍射出射光场内外环偏振态相同.造成上述出射光场内外环偏振态分布不同的原因是由入射光的形态不同.环形光锥形衍射出射光场的这一特殊偏振特性对双亮环的分离及其光场调控具有重要意义. 图2 (网刊彩色)高斯光锥形衍射出射光场在焦相面处偏振分布示意图Fig.2.(color online)The diagram of polarization characteristic of the conical di ff raction pattern under Gaussian beam. 2.3 实验与讨论 为了验证上面的理论计算结果的正确性,我们搭建了相应的实验系统.图3为线偏振环状高斯光束的锥形衍射实验系统原理图.实验系统由氦氖激光器、可调衰减片、扩束透镜L1、扩束透镜L2、环形光阑、起偏器、会聚透镜L3,KTP晶体和电荷耦合器件(CCD)组成,其中,透镜L1,L2和L3分别是焦距为10,150,100 mm的平凸透镜. 实验中使用如图4(a)所示的内、外半径分别为r1=9 mm,r2=10 mm的环形光阑;利用起偏器调节入射到晶体的线偏光偏振方向;实验用的双轴晶体是尺寸为5 mm×5 mm×10 mm的长方体状KTP晶体,在切割晶体时,令晶体的一个光轴沿着长方体的一个棱的方向,如图4(b)所示,C1和C2表示晶体的两个光轴,其中C1是平行于Ez轴的,图中赝矢量G代表晶体的方向,G由C1,C2光轴方向决定并垂直于两光轴所在的平面;实验时光束沿着Ez轴垂直晶体前表面入射. 图3 (网刊彩色)环状高斯光束的锥形衍射系统原理图Fig.3.(color online)Schematic diagram of conical di ff raction under annular Gaussian beam. 图4 (网刊彩色)(a)环形光阑和(b)KTP晶体的切割方向Fig.4.(color online)(a)Annular aperture and(b)the cutting direction of KTP crystal. 图5 线偏振环状光锥形衍射光场实验图 (a)α=22.5◦;(b)α =67.5◦;(c)α =112.5◦;(d)α =157.5◦Fig.5.The experimental results of conical di ff raction patterns with linearly polarized annular Gaussian beam:(a)α =22.5◦;(b)α =67.5◦;(c)α =112.5◦;(d)α =157.5◦. 图5(a)—(d)分 别 表 示 偏 振 方 向 为22.5◦,67.5◦,112.5◦和157.5◦的线偏振环状光束锥形衍射出射光场光强分布的实验结果.由图5(a)可知,当入射线偏光偏振方向为22.5◦时,锥形衍射出射光场的光外环在135◦的方位角处光强为零,而内环在315◦方位角处光强为零,即内环在315◦方位角和外环在135◦方位角处的偏振方向均为112.5◦;由图5(c)可得,当入射线偏光偏振方向为112.5◦时,锥形衍射出射光场的外环在315◦的方位角处光强为零,而内环在135◦方位角处光强为零,即内环在135◦方位角和外环在315◦方位角处的偏振方向均为22.5◦;因此可以得出,环形光束锥形衍射出射光场内、外环在相同方位角处的偏振态相互正交.同理,图5(b)和图5(d)也表明偏振方向为67.5◦和157.5◦线偏振环状光束的锥形衍射光场也具有相同规律.与图1中计算结果相比,理论和实验结果完全一致,图5中四幅实验图分别与图1(b),(d),(f)和(h)所示的理论仿真图一一对应,环上消光位置具有很好的一致性.因此可以证明,环形光束的锥形衍射出射光场内、外环在相同的方位角处具有相互正交的偏振态. 针对环状高斯光锥形衍射光内、外环具有完全正交的偏振分布特性,我们设计了一种具有特定偏振控制功能的组合偏振片,用于模拟环形光束锥形衍射出射光场的偏振分布,如图6所示.该组合偏振片由8块透振方向均不相同的扇形线偏振片组合而成,图6中蓝色箭头表示每块线偏振片的透振方向.此外我们还研究了组合偏振片对环光锥形衍射出射光场的调控. 图6 (网刊彩色)组合偏振片示意图Fig.6.(color online)The Schematic diagram of the combined polarizer. 为了分析组合偏振片对环光锥形衍射出射光场的调控,我们先计算了锥形衍射光偏振分布的琼斯矩阵,并以此近似表示组合偏振片的偏振矩阵.根据锥形衍射光场偏振分布特性,建立如图7所示的坐标系.图7中角度ϕ表示环上任意一点的方位角,α表示环上ϕ方位角处的偏振方向,则有:α=ϕ/2. 图7 (网刊彩色)锥形衍射光偏振分布的琼斯矩阵模型Fig.7.(color online)The Jones matrix model of the conical di ff racted beam. 由(8)式可知,经旋转角为δ的组合偏振片调制后的环形光束的锥形衍射出射光场强度为 经组合偏振片调制后的环形光锥形衍射出射光场的强度分布如图8所示.其中,左列为理论仿真结果,右列是与之对应的实验结果.图8(a)—(f)分别表示组合偏振片旋转角δ为0◦,30◦,150◦,180◦,210◦和300◦时环光锥形衍射出射光场分布.由图8(a)和图8(g)可以看出,当δ=0◦时,锥形衍射出射光场的内环消失了,只剩下外环.这是因为组合偏振片的偏振分布与锥形衍射出射光场的外环偏振分布完全相同,而与内环偏振分布完全正交,因此内环被彻底消除.随着δ的不断增加,锥形衍射出射光场的外环强度逐渐减弱,而内环强度逐渐增强;当δ=180◦时,组合偏振片与圆锥衍射外环完全正交,而与圆锥衍射内环相同,因此外环消失,如图8(d)和图8(j)所示;同理,随着δ继续增大,圆锥衍射外环开始逐渐增强,而圆锥衍射内环又逐渐变暗.组合偏振片旋转一周,交替出现内环或外环的消失现象,实现了对出射光场的调控. 图8 组合偏振片对环光锥形衍射出射光场的调控(a)—(f)理论图;(g)—(l)实验图;(a),(g) δ=0◦;(b),(h)δ =30◦;(c),(i)δ=150◦;(d),(j)δ =180◦;(e),(k)δ=210◦;(f),(l)δ=300◦Fig.8.The control results of conical di ff racted fi eld using the combined polarizer:(a)–(f)The theoretical results;(g)–(l)the experimental results;(a),(g)δ =0◦;(b),(h) δ =30◦;(c),(i) δ=150◦;(d),(j)δ =180◦;(e),(k)δ=210◦;(f),(l)δ =300◦. 实验中由于组合偏振片由多片偏振片拼接而成,受限于加工工艺不完善,相邻偏振片间存在缝隙,因此出现图8右列所示亮环不连续的现象.尽管存在亮环不连续问题,但是实验中锥形衍射出射光场中双环的强度变化趋势与理论仿真结果完全一致,证实了组合偏振片对环光锥形衍射出射光场的调控作用.组合偏振片对环光锥形衍射出射光场的特殊调控特性使得易于获得单个锥形衍射内环或外环,这种调控机制在光波的偏振复用与解复用方面具有重要的应用价值;此外,该光场调控机制在生物医学中的粒子操控以及光通信中的光开关等方面具有比较好的应用前景. 本文给出了环状高斯光束锥形衍射出射光场的光强公式,并从理论和实验两方面分析了环光锥形衍射出射光场的偏振特性.结果表明,环形光的锥形衍射出射光场为同心双环结构,并且内、外亮环具有正交的偏振分布.为实现对环光锥形衍射出射光场的调控,设计了一种由8块不同透振方向的扇形偏振片组成的组合偏振片,通过改变组合偏振片的旋转角,可以实现环光锥形衍射出射光场的周期性变化.并且当组合偏振片的旋转角δ分别为0◦和180◦时,可以分别消去锥形衍射光场的内环和外环,得到只有一个亮环的锥形衍射出射光场.通过组合偏振片的调控,得到一组内外环强度比可调的环形光场,该可调光场在光束整形、光镊、光开光、光波分复用等方面有较好的应用价值,推动了锥形衍射理论及应用的发展. [1]Lloyd H 1831 Lond.Edinb.Phil.Mag.2 112 [2]Born M,Wolf E 1999 Principles of Optics(seventh expanded edition)(Cambridge:Cambridge University Press)p904 [3]Lunney J G,Weaire D 2006 Europhys.News 37 26 [4]Belskii A M,Khapalyuk A P 1978 Opt.Spectrosc.44 436 [5]Poggendor ffJ C 1839 Pogg.Ann.48 461 [6]Voigt W 1905 Ann.Phys.Berlin 323 645 [7]Raman C V,Rajagopalan V S,Nedungadi T M K 1941 Proc.Math.Sci.14 221 [8]Portigal D L,Burstein E 1969 J.Opt.Soc.Am.59 1567 [9]Berry M V 2004 J.Opt.A:Pure Appl.Opt.6 289 [10]Turpin A,Loiko Y V,Kalkandkiev T K,Tomizawa H,Mompart J 2014 Opt.Lett.39 4349 [11]O’Dwyer D P,Phelan C F,Rakovich Y P,Eastham P R,Lunney J G,Donegan J F 2011 Opt.Express 19 2580 [12]Darcy R T,McCloskey D,Ballantine K E,Jennings B D,Lunney J G,Eastham P R,Donegan J F 2013 Opt.Express 21 20394 [13]Grant S D,Zolotovskaya S A,Gillespie W A,Kalkandjiev T K,Abdolvand A 2014 Opt.Lett.39 1988 [14]Peet V 2014 J.Opt.16 075702 [15]Turpin A,Loiko Y V,Kalkandjiev T K,Corbalán R,Mompart J 2015 Phys.Rev.A 92 013802 [16]Wu F T,Jiang X G,Liu B,Qiu Z X 2009 Acta Phys.Sin.58 2410(in Chinese)[吴逢铁,江新光,刘彬,邱振兴2009物理学报58 2410] [17]Zhu Q C,Wu F T,Hu R,Feng C 2016 Acta Phys.Sin.65 184101(in Chinese)[朱清智,吴逢铁,胡润,冯聪2016物理学报65 184101] [18]Liu S,Li P,Zhang Y,Han L,Cheng H C,Zhao J L 2016 Acta Opt.Sin.10 1026001(in Chinese)[刘圣,李鹏,章毅,韩磊,程华超,赵建林2016光学学报10 1026001] [19]O’Dwyer D P,Phelan C F,Ballantine K E,Rakovich Y P,Lunney J G,Donegan J F 2010 Opt.Express 18 27319 [20]Peinado A,Lizana A,Turpín A,Iemmi C,Kalkandjiev T K,Mompart J,Campos J 2015 Opt.Express 23 5636 [21]Turpin A,Kalkandjiev T K,Mompart J 2016 2016 15th Workshop on Information Optics Barcelona,Spain,July 11-15,2016 p1 [22]Tovar A A 2001 J.Opt.Soc.Am.A 18 1897 [23]Turpin A,Loiko Y V,Peinado A,Lizana A,Kalkandjiev T K,Campos J,Mompart J 2015 Opt.Express 23 5704 [24]Loiko Y V,Turpin A,Kalkandjiev T K,Mompart J 2012 Proc.SPIE 8246 82460T PACS:42.25.–p,42.25.Fx,42.25.Lc,42.25.JaDOI:10.7498/aps.66.124202 Polarization characteristic and control of the conical di ff racted output fi eld under annular beam∗ Du Chuang Jia Da-Gong†Zhang Hong-Xia Liu Tie-Gen Zhang Yi-Mo (Key Laboratory of Opto-electronics Information Technology,Ministry of Education,School of Precision Instrument and Opto-Electronics Engineering,Tianjin University,Tianjin 300072,China) 8 January 2017;revised manuscript 24 March 2017) Conical di ff raction,a unique optical phenomenon in biaxial crystal,has important applications for the manipulation of particles.In this paper,a new model of annular Gaussian beam is constructed based on the Tovar’s fl at-topped multi-Gaussian laser beams.The conical di ff raction of annular Gaussian beam is calculated using Belsky-Khapalyuk-Berry theory.The polarization characteristics of conical di ff racted output beams under the annular Gaussian beam are theoretically calculated and experimentally demonstrated by means of the linearly polarized annular Gaussian beams with di ff erent polarization directions.It is found that the same azimuth angles of the inner and outer rings of the conical di ff racted output beams have orthogonal polarization characteristics.A combined polarizer(CP)composed of eight polarizing segments with di ff erent speci fi c pass axes of polarization is presented to simulate the polarization characteristic of the optical fi eld of conical di ff raction.Furthermore the calculations for output- fi eld control of conical di ff raction under the annular beam by using the proposed CP are compared with the experimental results.The results show that the intensities of both the inner and outer rings are periodically varied with CP azimuth angle.And when the azimuth angle of CP is 0◦,only the conical di ff racted outer ring is remained,while only the inner ring of conical di ff raction is remained for 180◦.This tunable conical di ff racted fi eld has important applications in optical tweezers and wavelength division multiplexing. biaxial crystal,conical di ff raction,annular Gaussian beam,combined polarizer 10.7498/aps.66.124202 ∗国家自然科学基金(批准号:61377077)和国家重点基础研究发展计划(批准号:2014CB340103)资助的课题. †通信作者.E-mail:dagongjia@tju.edu.cn ©2017中国物理学会Chinese Physical Society http://wulixb.iphy.ac.cn *Project supported by the National Natural Science Foundation of China(Grant No.61377077)and the National Basic Research Program of China(Grant No.2014CB340103). †Corresponding author.E-mail:dagongjia@tju.edu.cn
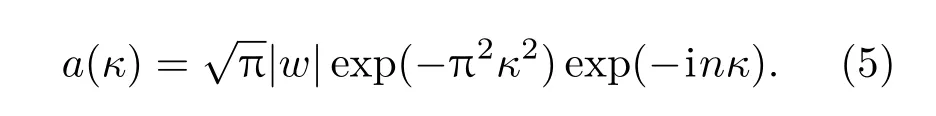

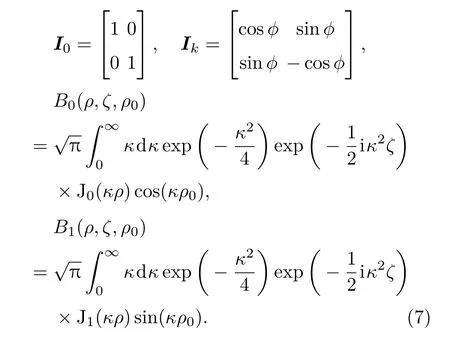
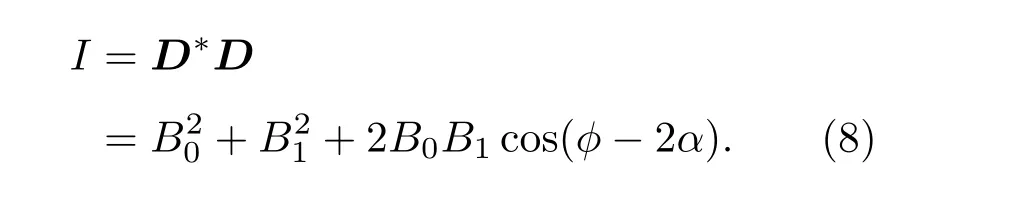



3 组合偏振片对环光锥形衍射光场的调控

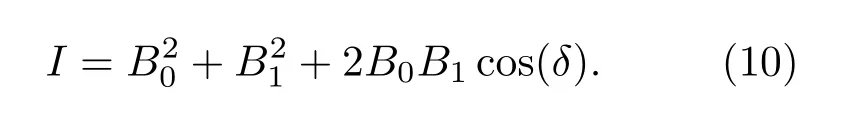

4 结 论
