存在障碍物时电波传播抛物线方程分析及其验证∗

魏乔菲 尹成友 范启蒙

(电子工程学院,脉冲功率激光国家重点实验室,合肥 230037)

存在障碍物时电波传播抛物线方程分析及其验证∗

魏乔菲 尹成友†范启蒙

(电子工程学院,脉冲功率激光国家重点实验室,合肥 230037)

(2017年1月14日收到;2017年3月20日收到修改稿)

双向抛物线方法主要用于起伏地形下电波传播问题的计算,该算法本身无法处理地面存在障碍物,尤其是真实环境下障碍物与地面为不同媒质的情况.因此本文提出一种用于存在障碍物时电波传播计算的抛物线方程新算法.该方法采用区域分解,对不同障碍物区域的场值进行分区计算,并对计算结果进行相位修正,从而实现该情况下空间中场值的计算.在此基础上,使用矩量法来精确验证抛物线方法的计算精度.通过实例分析,证明了存在障碍物时新算法的精确性,为之后求解真实环境下的电波传播问题提供了参考.

抛物线方程,电波传播,区域分解,矩量法

1 引 言

近年来,双向抛物线方法[1−3]已经逐步成为对流层电波传播问题研究中最常用的方法.该算法可以计算不规则地形特征和不同电磁参数的地表结构对电波传播的影响,在不规则地形的处理方面,抛物线方法[4−7]的计算精度受限于起伏地形的倾角[8−10],倾角超过一定范围后,双向抛物线方法的计算存在较大误差.这种下边界条件的处理方式只是将障碍物当起伏地形处理,没有考虑障碍物内存在的场值对空间中场值的影响.因此,当地面存在障碍物时,抛物线方法计算存在困难.

在抛物线方法的计算精度验证方面,通常在不规则地形下使用AREPS软件[11]或高频近似法[12−14]来验证抛物线方法计算的正确性,高频近似法主要有菲涅耳积分法及几何光学结合一致性几何绕射理论法两种方式.这两种方法都是基于射线追踪法来计算空间中场强的分布,因为这两种高频近似法在计算过程中都忽略被障碍物反射的场值,所以主要用于前向抛物线方法计算的验证.与此同时,障碍物情况越复杂,空间中绕射场的场值计算越困难.除此之外,当波源传播角度较大时,为提高近场区域的验证精度,Omaki等[15]提出用时域有限差分方法[16]验证抛物线方法计算结果的精确性.

结合上述情况,本文在原有起伏地形下双向抛物线方法计算方式的基础上,提出了一种新的抛物线方程算法,该算法可以较为精确地计算地面存在障碍物时空间中的场值大小.当地面存在障碍物时,根据区域分解原理[17]将障碍物处的场值计算分为两部分,并分别增加一段重叠区域,以满足障碍物上边界处场值计算的连续性.针对不同区域的场值计算,使用不同的抛物线计算方法.除此之外,在场值的迭代计算中对总场计算时的相位差异和障碍物传播中造成的相位差异两方面都进行了相位修正.在新算法的验证方面,本文用矩量法[18]来验证近距离下双向抛物线方法求解电波传播问题的计算精度.最后通过一系列实例分析验证了新算法计算的精确性.

2 障碍物下抛物线方程的处理方法

设电磁场的时谐因子为exp(jωt),本文主要计算讨论的是地面存在障碍物时双向抛物线方法的具体求解,假设地面为理想导体,障碍物近似如图1所示.

图1 障碍物(矩形)模型Fig.1.The model of obstacle(rectangle).

图1中ht,hr,h分别代表源的发射高度、观察点的接收高度和障碍物的高度.在此基础上,本节主要就双向抛物线方法计算中的波源设置、基本原理以及对计算结果的相位修正三个方面进行分析说明.

2.1 初始场设置的等效源模型

常用的抛物线方法的波源设置是利用远场与近场之间的关系反推初始场表达式,这种初始场u(0,z)的设置方法存在波束较窄或天线架高不能满足u(0,z)=0(z<0)时,初始场会延伸到地面以下的问题,并且这种方法没有建立起初始场与天线电流分布之间的直接联系.结合上述情况,本文使用等效源模型来逼近初始场设置[19,20].

已知抛物线方程由初始场推导出的自由空间远区场u(x,z)的解析形式如下[21]:

其中H(2)1表示一阶第二类汉克尔函数,ρ为源点到场点的距离,k为自由空间的波数.现假设有一个在y方向无限长的有具体分布数值横向磁流带,电流方向为z方向,

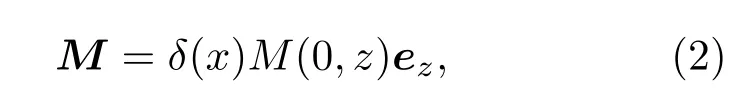
则该电流产生的电场为

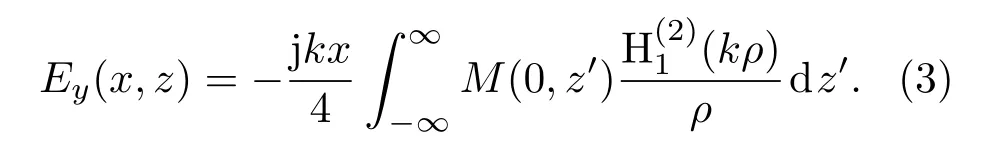
由(3)和(1)式,可以看出两者具有相似的形式.根据对偶定理,同理可推导出等效电流产生的磁场表达式,由此推出初始场与等效源的关系如下:

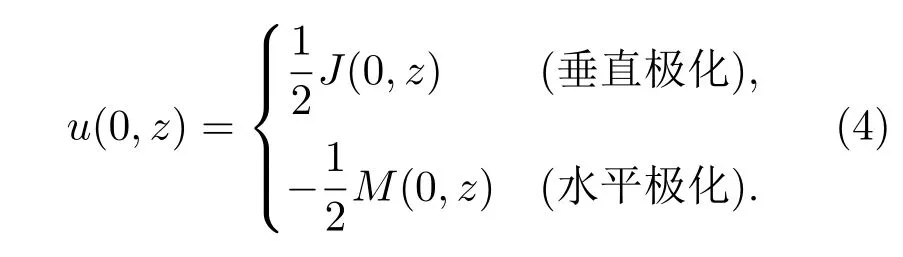
在(4)式的基础上,可以通过等效源直接逼近抛物线方法的初始场设置,这种初始场设置建立了其与天线电流分布之间的直接联系,不仅解决了之前方法存在的问题,而且为后面利用矩量法分析验证抛物线方程的计算精度提供了统一的入射源环境.

2.2 双向抛物线方法的基本原理

在球面周向均匀起伏的地形下,通常使用双向抛物线方法来求电波传播问题.已知根据平坦地球模型,可得电磁场满足二维标量波动方程:

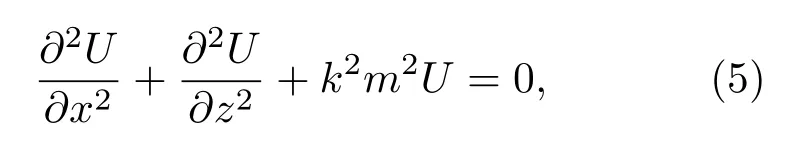
其中U表示电磁场量Ey,Hy;m代表修正后的大气折射率.为解调(5)式中的相位快变部分,在波动方程的基础上引入轴向衰减因子如下[1−3]:

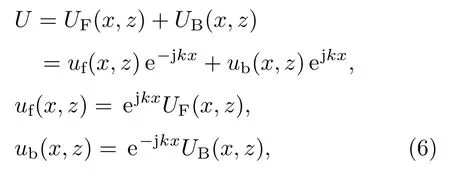
其中UF,UB代表前向场和后向场.将(6)式分别代入(5)式,并使用Feit-Fleck宽角近似处理,得到双向波动方程为

当地面为理想导体时,通过分步傅里叶方法求得双向抛物线方法的步进公式如下:

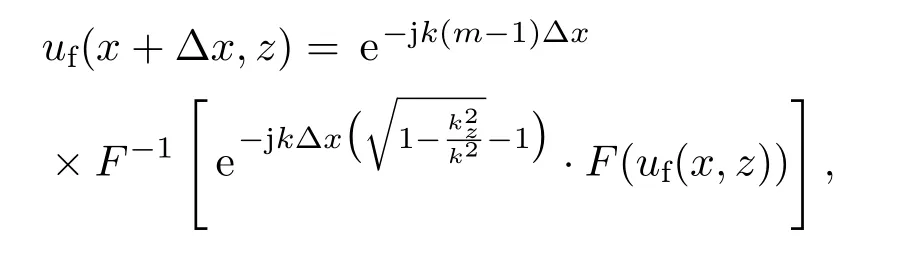
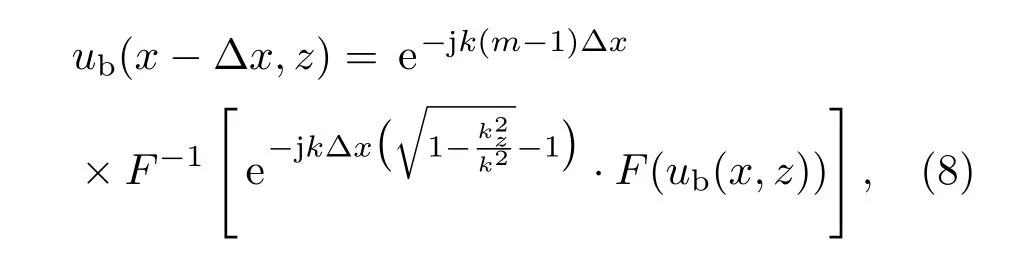
其中F和F−1分别代表傅里叶变换和逆变换.可以看出在忽略传播方向的前提下,推导出的步进公式是完全一致的.为进一步分析双向抛物方程在不规则地形下的具体实现方法,以图1中的障碍物模型为例,文献[1]中双向抛物线方法的计算方式如图2所示.

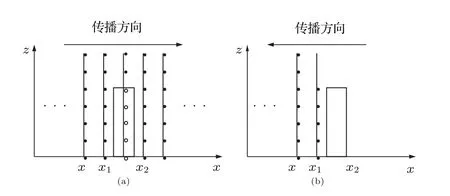
图2 单矩形障碍物下空间场值的处理 (a)前向传播场;(b)后向传播场Fig.2.The processing of spatial fi eld under single rectangular obstacle:(a)The forward fi eld;(b)the backward fi eld.

以图2中对单矩形障碍物的处理方式,可得空间中场值设定如下:

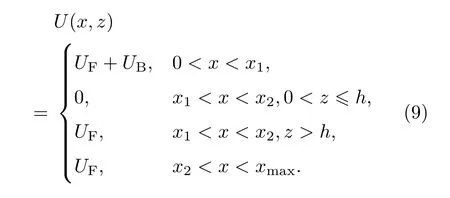
由(9)式可以看出,当迭代计算到障碍物时,障碍物之下的场值被强行置零,只计算上空间的场值.文献[1]中的这种计算方式将障碍物视为起伏地形,没有考虑障碍物内透射场的存在,也没有考虑不同极化下障碍物边界处场值的处理.

2.3 双向抛物线方法的相位补偿

在(9)式中场值分类的基础上,双向抛物线方法求解空间中总场如(6)式所示,是将前向和后向波统一到一个坐标原点得出的,在叠加计算时忽略了前向场与后向场相位不一致的问题.从图2(b)中对后向传播场的处理中可以看出后向波源是在x1处产生的,根据障碍物反射面x1处的边界条件可得

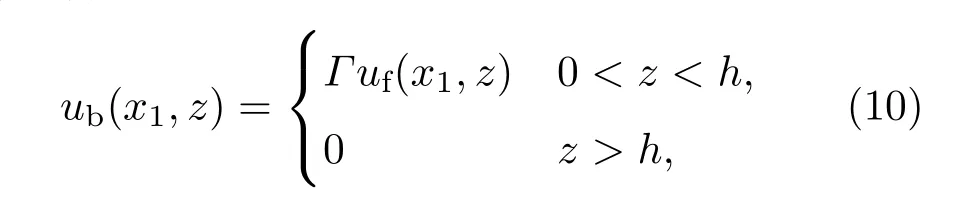
其中Γ为自由空间向障碍物垂直入射下的反射系数.在迭代求解空间中任意一点x处的总场时,可以看出前向波是从原点出发,后向波是从x1出发,此时x点的场强应该为

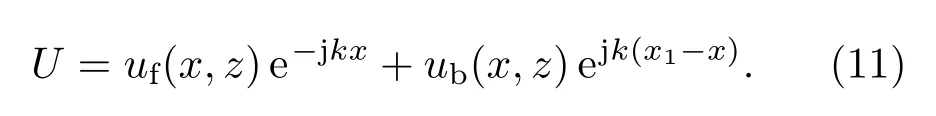
对比(11)式与(6)式得,在求解总场时,需要先进行相位补偿将前向波与后向波的相位统一后叠加.将(11)式代入(6)式得

通过(12)式可以修正双向抛物线方法总场计算时的相位差异,但是在此之前的计算处理都是将障碍物处理为起伏地形,没有从根本上处理存在障碍物时空间中的场值该如何计算的问题.因此本文提出一种新的抛物线方程计算方法,将障碍物处场值的计算进行单独处理.

3 存在障碍物时抛物线方程的处理方法

当地面存在障碍物时,经典的抛物线方法是将障碍物与地面视为整体,将起伏地形之下的场值全部置零,并根据地面媒质参数的不同,使用不同的分步傅里叶变换法.这种计算方法存在以下两方面的问题:第一方面是因为该方法的计算精度受限于障碍物的倾角大小;第二方面是没有考虑障碍物内部场值对空间中场值分布的影响.本文提出了一种区域分解算法.

3.1 区域分解算法

以图2中对单矩形障碍物的处理为例,经典抛物线方法的计算区域是从地面一直到吸收层.本文在此基础上,对障碍物区域场值的求解进行了分区处理,当步进求解到障碍物处,场值的计算分为两部分,第一部分是障碍物之上的场值计算,第二部分是障碍物之下的场值计算.根据区域的不同,采用不同的离散傅里叶变换方法,并对障碍物上边界处的场值计算加以修正.根据区域分解原理,对场值计算处理如下.

由图3可以看出,障碍物区域的场值计算主要分为三部分.

1)障碍物上半空间的场值计算.由图3可以看出,计算障碍物上半空间的场值时,该区域中的下边界从障碍物的上边界B点往障碍物之下延伸了一段,这种延伸方式是为了避免对区域突然截断时造成的计算误差.对重叠区延伸长度的选择与计算精度有关,通常为了计算方便,直接取障碍物高度的一半.在此基础上,此时上空间的下边界不再是理想导体而是均匀介质,所以上半空间的迭代计算相当于阻抗边界下的混合傅里叶求解.对下边界的处理等效为Leontovich阻抗边界条件[21]

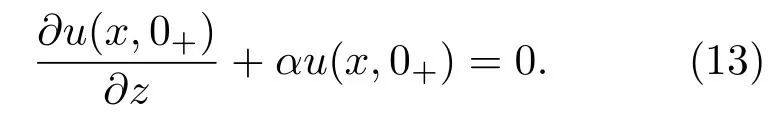
根据(13)式,通过离散混合傅里叶变换法就可以求解障碍物之上包括重叠区域的场值.

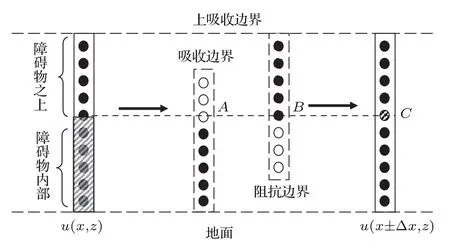
图3 障碍物处场值计算的区域分解Fig.3.Domain decomposition of fi eld calculation in obstacle zone.

2)障碍物内部空间的场值计算.此时介质障碍物内场值计算的上边界也发生了改变,为了提高计算精度,直接将障碍物内部的场值计算扩充到整个空间中,因为地面仍是导体,所以下边界的处理使用导体边界条件,傅里叶变换采用正弦变换计算,最后出障碍物恢复空间场值时只提取障碍物高度h以下区域的场值.

3)求解完障碍物上下空间的场值后,如图3所示,在求解障碍物u(x±∆x,z)时,需要对介质障碍物上边界C处的场值进行修正.该点处场值计算如下:

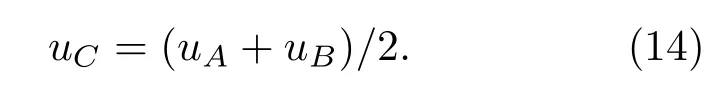
(14)式是将连接的边界点处的场值使用两种区域算法的平均值代替,这样确保边界切向场连续.

综上,在整个空间的迭代计算中遇到障碍物处就将计算区域按图3所示分成两部分计算,其余平坦区域的场值计算方法不变.

3.2 介质中抛物线方程的处理及相位补偿

在图3的基础上,障碍物之下的场值计算等效于介质体内的电波传播问题的求解.因为地面仍为理想导体,所以在障碍物内的迭代计算与自由空间的迭代计算相比区别在于空间中的折射率发生了改变,等效为(6)式的解调因子的改变:

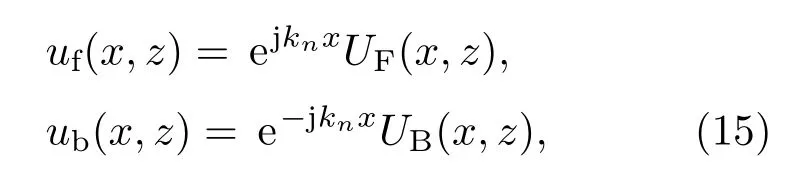
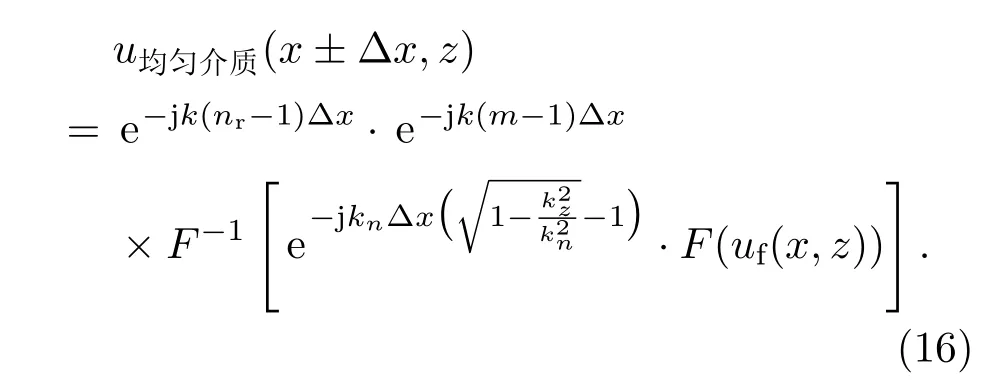
在(16)式步进求解的基础上,还需要考虑进出障碍物时电磁波的透射作用,场值修正为

当障碍物为理想导体时,因为障碍物内不存在场值,所以只需要考虑上半空间的场值求解.又因为此时上半空间的下边界为导体,所以根据极化模型的不同,混合傅里叶变换法也简化为正弦或余弦傅里叶变换法,并在恢复场值时,直接将下半空间的场值赋零.

4 双向抛物线方程矩量法验证分析

为了验证所提算法的精度,本文提出在近距离下用矩量法精确求解空间中的场强分布,从而验证存在障碍物的情况下新算法计算结果的精确性.因为障碍物为理想导体,也等效为一种均匀介质,所以下面主要考虑矩形障碍物为均匀介质的情况,并分别从两种极化角度出发分析讨论矩量法的处理过程.

如图1所示的障碍物,将地面影响等效到格林函数G中,只对障碍物采用矩量法分析进行处理.由于障碍物为均匀介质,所以可以用Poggio-Miller-Chang-Harrington-Wu(PMCHW)方程和体等效两种方法来求解空间中的场强分布,本文选择PMCHW方程组来联立求解上述问题:

其中Hi,Ei,J,M分别代表入射磁场、入射电场以及障碍物表面的等效电流与等效磁流;z1,z2分别指自由空间和均匀介质障碍物内的波阻抗.L(X),K(X)都是简化表达的算子,定义如下:

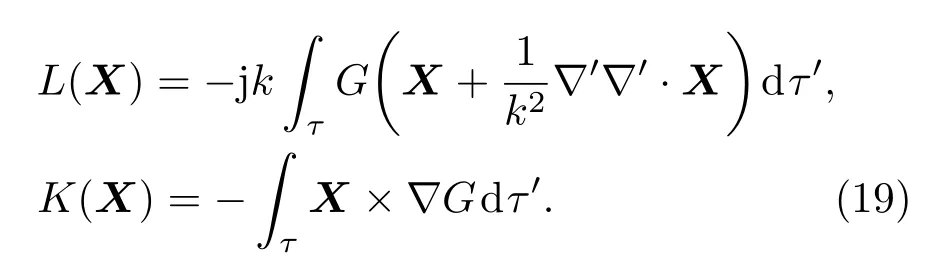
联立(19)式中的算子,通过(18)式中等效电磁流与入射场之间的关系可以实现任意极化下空间中的场值求解.因为存在导体地面,考虑地面镜像作用,对于电磁流源,(19)式中的二维格林函数为

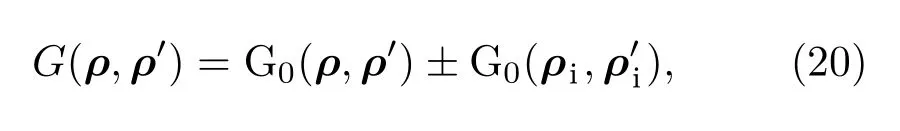
其中ρi,ρ′i代表源点及其镜像点的位置矢量,G0表示零阶第二类汉克尔函数,镜像格林函数的正负取决于等效电磁流的镜像原理.因为在求解过程中存在二阶导数的计算,所以对于纵向电磁流采用点匹配脉冲基求解,横向电磁流基函数和检验源均采用三角基函数矩量法求解.

在TE波(垂直极化)照射下,障碍物在空间中产生的散射磁场只有y分量.因此使用二维等效电流来逼近抛物线方法的初始场,在垂直极化下,障碍物表面会产生环向的等效电流,流向同图1,障碍物表面的等效磁流为y向,进而求得空间中总场如下:

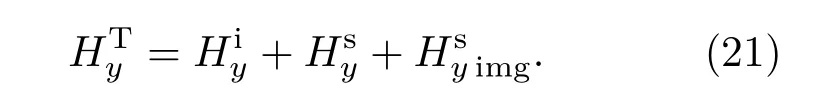
在TM波(水平极化)照射下,空间中只有y向电场,因此使用二维的等效磁流来等效初始场,在水平极化下,障碍物表面的等效电流为y向,等效磁流变成环向,积分方程中的各项分量的求解可以通过对偶原理从(21)式直接求得,惟一的区别在于考虑镜像作用时,镜像电流的等效与镜像磁流的等效相反.同理求得空间中总电场如下:

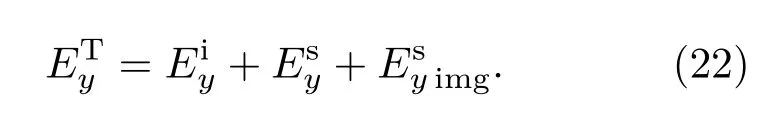
5 计算实例和结果分析

本文分析的问题基于图1所示的矩形障碍物模型,用矩量法计算近距离下电波传播的具体场值,从而验证在存在障碍物情况下新算法计算结果的精确性,并在障碍物为理想导体的情况下将新算法与文献[2]的PEtool抛物线方法进行对比分析.在下述实例分析中,矩量法的剖分间隔为0.5 m,新算法的步进间隔是1 m,并且所有实例都是在i5处理器、32位操作系统、4G内存的计算机设备环境下运行仿真的.

实例一:发射源工作频率30 MHz,高度为200 m,其发射波束仰角0◦,波束宽度20◦,水平极化,辐射源等效辐射功率为W,Z0为自由空间波阻抗.障碍物为双矩形理想导体,矩形模型形状一致,第一个矩形模型位于距离发射源750 m处,第二个矩形模型位于距离发射源900 m处,障碍物模型宽50 m,高度100 m.计算得到在接收高度为80 m处场强随水平距离变化的场强振幅分布如图4(a)所示,图4(b)为图4(a)的局部展开结果,其中MoM代表矩量法计算结果,PE2代表本文提出的存在障碍物情况下基于双向抛物线方程的新算法的计算结果,PEtool代表文献[2]算法求得的空间场值.

分析图4(a)可以看出:障碍物后新算法的计算结果与矩量法相比幅度基本一致,障碍物之前的场值振荡较为剧烈,造成这种现象的原因是地面反射波与直达波叠加相互作用产生的;障碍物之间的场值振荡是因为障碍物之间存在反射场的多次叠加.障碍物之后场值的抬高是因为随距离增加,导体障碍物的绕射场从深阴影区逐步过渡到直达波能够照射到的亮区.由图4(b)可以看出PEtool算法的计算结果与新算法和矩量法相比起伏的相位出现了偏移,幅度也不完全一致.从而说明边界处理和相位修正对双向抛物线方法的计算精度有较大的改善,验证了新算法在障碍物为理想导体情况下的精确性.

图4 (网刊彩色)水平极化双矩形模型场值对比 (a)整体场值;(b)局部场值Fig.4.(color online)The contrasts of fi elds for horizontal polarization under double rectangular models:(a)The whole fi elds;(b)the local fi elds.

实例二:验证水平极化下图1中单矩形介质障碍物模型下新方法计算结果的精确性,介质的参数为εr=4,σ=10−5s/m,将发射源的波束宽度更改为30◦,单矩形介质障碍物距离波源750 m,障碍物宽度变为20 m,其余参数与实例一相同,计算的接收高度在80 m处场强随水平距离变化的场强振幅分布如图5所示,图5(b)为图5(a)的局部展开结果.

分析图5可以看出,当障碍物为均匀介质时,新算法的计算结果与矩量法相比幅度基本一致,尤其是障碍物之后800 m以上,在波形变换凹口处也完全一致,因此可以得出当存在障碍物时,使用分区原理以及介质内的相位分布修正方法可以有效地计算此时空间中的场值大小,也验证了新算法在障碍物为均匀介质情况下的精确性.

在该实例中,矩量法的计算时间为335 s,新算法的计算时间为5 s,在计算精度几乎一样的情况下,新算法的计算时间比矩量法快了将近67倍,从而验证了新算法计算的有效性.

图5 (网刊彩色)单矩形介质障碍物场值对比 (a)整体场值;(b)局部场值Fig.5.(color online)The contrasts of fi elds under single rectangular dielectric obstacle:(a)The whole if elds;(b)the local fi elds.

实例三:在实例一参数的基础上将发射源的波束宽度改为30◦,双矩形宽度改为20 m,其余参数不变,双矩形均匀介质障碍物的介电常数同实例二,计算水平极化下接收高度为80 m处场强随水平距离的变化如图6所示,图6(b)为图6(a)的局部展开结果.

从图6可以看出,在双矩形均匀介质障碍物模型下,新算法与矩量法的计算结果相比,场值变换趋势基本一致.由图6(b)中双矩形障碍物之间的场值比较可以看出,新算法与矩量法的计算结果相比误差非常小,从而体现了新算法计算的精确性,此时矩量法所需的时间为1097 s,而新算法的计算时间仅为65 s.当地形变换更为复杂时,矩量法的计算难度会迅速增大甚至无法计算,新算法的优势性会更进一步体现.在此基础上,对于双向情况下新算法对障碍物内的计算误差有待进一步研究.

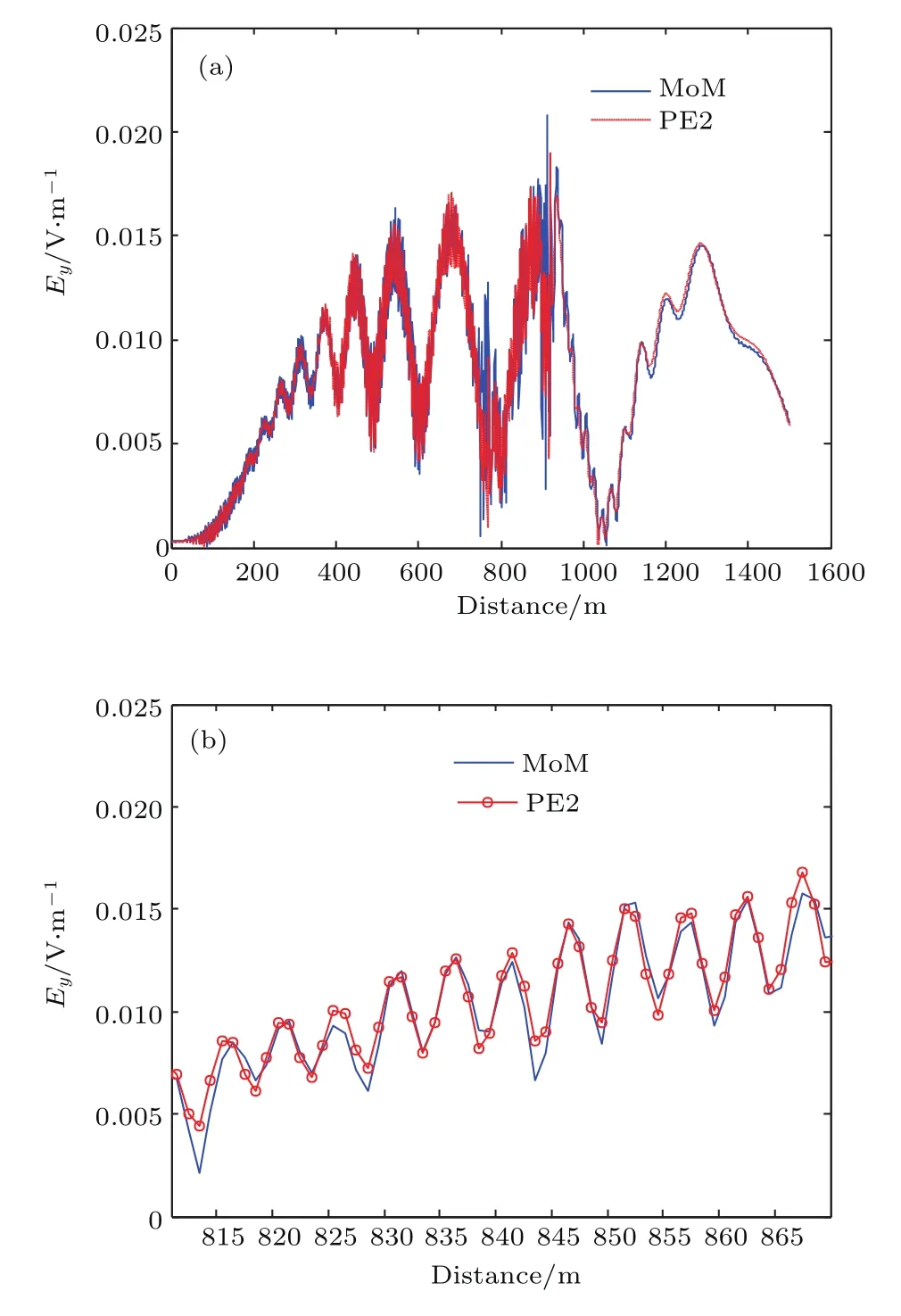
图6 (网刊彩色)双矩形介质障碍物场值的对比 (a)整体场值;(b)局部场值Fig.6.(color online)The contrasts of fi elds under double rectangular dielectric obstacles:(a)The whole if elds;(b)the local fi elds.

6 结 论

经典的抛物线方法只能用于求解起伏地形下的电波传播问题的计算,当地面存在障碍物时,尤其是两种媒质介质参数不同的情况下,双向抛物线方法无法计算.本文基于双向抛物线方法的基本原理,提出了一种新的区域分解算法,对存在障碍物时空间中的场值计算进行了区域分解处理,并对均匀介质内双向抛物线方法的求解给出了计算公式.通过上述方法,使得基于抛物线方程的新算法可以处理地面存在障碍物的情况.在此基础上,对求解总场时的前向场与后向场的相位以及出介质障碍物边缘时上下空间的场值叠加时的相位都分别进行了修正,修正方法有效改善了新算法计算的空间中场值的相位匹配性.最后,结合矩量法在近距离下对算法在存在障碍物环境下的电磁传播计算结果进行了验证分析,通过实例分析,验证了基分区原理的双向抛物线方程新算法计算出场值的精确性以及优越性.

[1]Ozlem O 2009 IEEE Trans.Antenn.Propag.57 2706

[2]Ozlem O,Gokhan A,Mustafa K,Levent S 2011 Comput.Phys.Commun.182 2638

[3]Wang K,Long Y L 2012 IEEE Trans.Antenn.Propag.60 4467

[4]Zhang P,Bai L,Wu Z S,Guo L X 2016 IEEE Trans.Antenn.Propag.Mag.58 31

[5]Wang D D,Xi X L,Pu Y R,Liu J F,Zhou L L 2016 IEEE Trans.Antenn.Wireless Propag.Lett.15 734

[6]Yuan X J,Lin W G 1993 Chin.Phys.Lett.10 57

[7]Omaki N,Yun Z Q,Iskander M F 2012 2012 IEEE International Conference on Wireless Information Technology and Systems(ICWITS)Maui,USA,November 11–16,2012 p1

[8]Kuttler J R 1999 IEEE Trans.Antenn.Propag.47 1131

[9]Donohue D J,Kuttler J R 2000 IEEE Trans.Antenn.Propag.48 260

[10]Beilis A,Tappert F D 1979 J.Acoust.Soc.Am.66 811

[11]Wang Y J,Guo L X,Li Q L 2016 11th International Symposium on Antennas,Propagation and EM Theory(ISAPE)Guilin,China,October 18–21,2016 p404

[12]Ozgun O,Sevgi L 2012 Aces J.27 376

[13]Gokhan A,Levent S 2013 IEEE Trans.Antenn.Propag.Mag.55 244

[14]Zhu J,Yin C Y,Wei Q F 2016 J.Microwaves 32 32(in Chinese)[祝杰,尹成友,魏乔菲 2016微波学报 32 32]

[15]Omak N,Yun Z Q,Iskander M F 2012 Antennas and Propagation Society International Symposium(APSURSI)Chicago,USA,July 8–14,2012,p1

[16]Lu J,Zhou H C 2016 Chin.Phys.B 25 90203

[17]Pvel V,Pvel P 2007 IEEE Antenn.Wireless Propag.Lett.6 152

[18]Sheng X Q 2004 Computational Electromagnetic Theory(Beijing:Science Press)pp49–53(in Chinese)[盛新庆2004计算电磁学要论(北京:科学出版社)第49—53页]

[19]Zhu J,Yin C Y 2016 J.Microwaves 32 26(in Chinese)[祝杰,尹成友 2016微波学报32 26]

[20]Yin C Y,Zhu J,Wei Q F 2016 37th Progress in Electromagnetics Shanghai,China,August 8–11,2016 p1655

[21]Levy M 2000 Parabolic Equation Methods for Electromagnetic Wave Propagation(London:IEE Press)pp149,287–291

PACS:41.20.JbDOI:10.7498/aps.66.124102

Research and veri fi cation for parabolic equation method of radio wave propagation in obstacle environment∗

Wei Qiao-FeiYin Cheng-You†Fan Qi-Meng

(National Key Laboratory of Pulsed Power Laser Technology,Electronic Engineering Institute of PLA,Hefei 230037,China)

14 January 2017;revised manuscript

20 March 2017)

In recent years,the two-way parabolic equation method(2WPE)has been widely utilized for studying the tropospheric ground-wave propagation under the irregular terrain.This algorithm can deal with the in fl uences of the irregular terrain characteristic and the di ff erent electromagnetic parameters of the surface structure on wave propagation.However,there are still some defects in 2WPE method.Firstly,the method considers the irregular terrain and obstacles as a whole,so it cannot deal with the situation where the medium parameters of obstacles and the ground are di ff erent.Secondly,its calculation precision is limited with the inclination of the undulating terrain:if there are obstacles the upper bound of the inclination is easily broken through.Therefore,in this paper,a novel two-way parabolic equation method is proposed for analyzing the radio wave propagation in obstacle environment.According to the principle of domain decomposition,the obstacle zones are divided into two domains in the new algorithm,and the two subdomains are calculated,respectively.Meanwhile,in order to avoid the calculation error caused by the abrupt truncation of the obstacle zone,the fi eld at the upper boundary of obstacles is modi fi ed to ensure the continuity of tangential fi eld.To further improve the accuracy of the new algorithm,according to the historical transmission paths,we exactly retrieve the phases of each forward and backward wave,especially when stepping in and out of the obstacles.Furthermore,the method of moment(MoM)is used to verify the calculation accuracy of the new algorithm in obstacle environment.Although the accuracy of the MoM is very high,it also requires a great deal of calculation resources:it can only be employed to compute the fi elds in short distance.To overcome the difficulty,we use the image principle in the obstacle environment and do not subdivide the ground into segments;therefore the veri fi cation accuracy can be improved.On this basis,to unify the source setting of the new algorithm and the MoM,the equivalent source model is used to set the initial fi eld.Finally,through numerical experiments,the simulation results of both methods agree very well,so the e ff ectiveness of the boundary correction and the phase correction which are presented in this paper are both veri fi ed.The accuracy and superiority of the new algorithm in obstacle environment are also demonstrated.To sum up,the novel two-way parabolic equation method can be used to accurately calculate the fi eld of the space in the obstacle environment,and lays the foundation for the fi eld calculation of radio wave propagation in real environment.

parabolic equation,radio wave propagation,domain decomposition,method of moment

10.7498/aps.66.124102

∗总装备部预研基金(批准号:51333020201)资助的课题.

†通信作者.E-mail:cyouyin@sina.com

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the General Equipment Department Pre-Research Foundation,China(Grant No.51333020201).

†Corresponding author.E-mail:cyouyin@sina.com