考虑收益波动性的风险厌恶型报童问题

田志勇，周 丽，袁瑞萍

（北京物资学院 信息学院，北京 101149）

考虑收益波动性的风险厌恶型报童问题

田志勇，周 丽，袁瑞萍

（北京物资学院 信息学院，北京 101149）

将报童收益波动性融入目标函数，以价格和库存量作为决策变量，针对单期、加法形式的随机需求函数和风险厌恶型报童建立模型。分别利用顺序优化和同时优化的方法对模型进行研究，分析了模型最优解与风险系数和剩余库存处理单价等参数的关系，利用弹性概念描述了模型最优解存在的条件及实际意义。研究表明两种方法的最优解具有相同的性质—价格和库存量都是风险系数的减函数、是剩余库存处理单价的增函数。关于最优解存在条件，同时优化的局部最优解要求最为宽松，全局最优解要求最严格，而顺序优化最优解的要求则介于两者之间。这些研究结论为企业辨析决策环境、进行有效决策提供了有益的参考。

报童模型；收益波动性；风险厌恶型；弹性

1 引言

报童问题的经典模型是以报童期望收益为目标函数、库存水平和价格为决策变量，研究其最优化问题[1-2]。一般地，单期报童收益包括三部分：报童销售收入、剩余存货价值和潜在销售损失。对于需求确定性问题来说，无论目标函数包含哪部分，问题的抽象模型不会出现本质差异。而对于包含随机性问题来说，报童收益三部分的数学表现和性质有较大差异，会对模型分析的复杂程度、最优解特征甚至结论产生重要影响。多数的研究，如xu等[3-4]、Dogan[5]、Jadidi等[6]、Khouja[7]，目标函数包含了三部分。少数研究则只包含部分收益，如Gerchak等[8]包含第二、三部分，Chua等[9]和丁小东等[10]只考虑了第一、二部分，而Javier等[11]则仅考虑了第一部分。采用收益的哪部分作为目标函数，需要根据研究的目的、进展和应用场景而定。但一般来说，采用部分报童收益的研究多是一种新的研究应用的开始，随着研究的深入，会逐步将报童收益的三个部分包含进来。

但仅以期望收益作为模型优化的目标函数，与报童决策的真实情景仍有较大差距。因为收益的波动显然也是报童决策时要考量的因素，在某种情况下，甚至可能会成为影响报童决策的关键因素。比如，著名的6σ管理，其核心就是“不是关于平均数的问题，而是关于方差或波动的问题”[12]。对风险的度量主要有三种[13]：均值方差类应用、在险价值VaR和条件风险价值CVaR。目前，VaR和CVaR应用于报童风险监控的研究文献比较多，如文献[14]、[15]、[16]和[17]等。但VaR和CVaR均是测度和控制报童收益处于风险（达到或达不到预定点）的概率，并未直接考量收益的波动性。而均值方差的研究文献则集中在需求或供应层面，直接应用在成本或收益层面的文献很少。需求波动虽在一定程度上可以看作利用需求概率函数间接地考量了收益波动（方差），但由于需求的波动性需要通过一定的函数关系传递到收益层面上，这种函数关系往往比较复杂，必然会导致直接在收益层面研究波动性在技术上更为复杂。但需求-收益函数关系使两个层面的波动性呈现出什么样的不同特征？对报童决策又将产生什么样的影响？这些都需要针对收益的均值方差专门研究。据作者所知，文献[11]是这一领域第一篇直接在收益层面考虑波动性的研究，但该文献考虑的报童收益还仅仅是报童销售收入，也即前面提及的第一部分。本文在以下方面进行了扩展：（1）目标函数中增加剩余库存价值，即包含了报童收益的第一和第二部分；（2）对顺序优化的两种情况进行了较系统地分析；（3）从本质上分析顺序优化和同时优化之间的区别与联系。

2 模型构建

2.1 需求函数

本文采用需求函数的加法形式

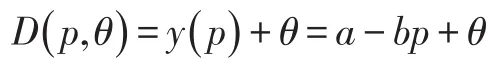
D表示需求,是价格p和随机因素θ的函数。y(p)=a-bp为确定性需求函数，p为价格,a＞0为市场规模，b＞0为需求对价格反馈系数。θ为随机变量，取值范围为[A,B]，且 A≤0,B≥0，期望 E(θ)=μ ，方差V(θ)=σ2,概率密度和概率分布函数分布为f(.)和F(.)，设概率分布函数的补函数为

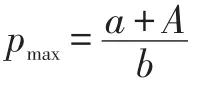
2.2 目标函数

设q为库存水平或订货批量，s为剩余库存处理单价。一般来说，有c＞s。在单期情况下，考虑剩余存货价值的报童利润函数为：

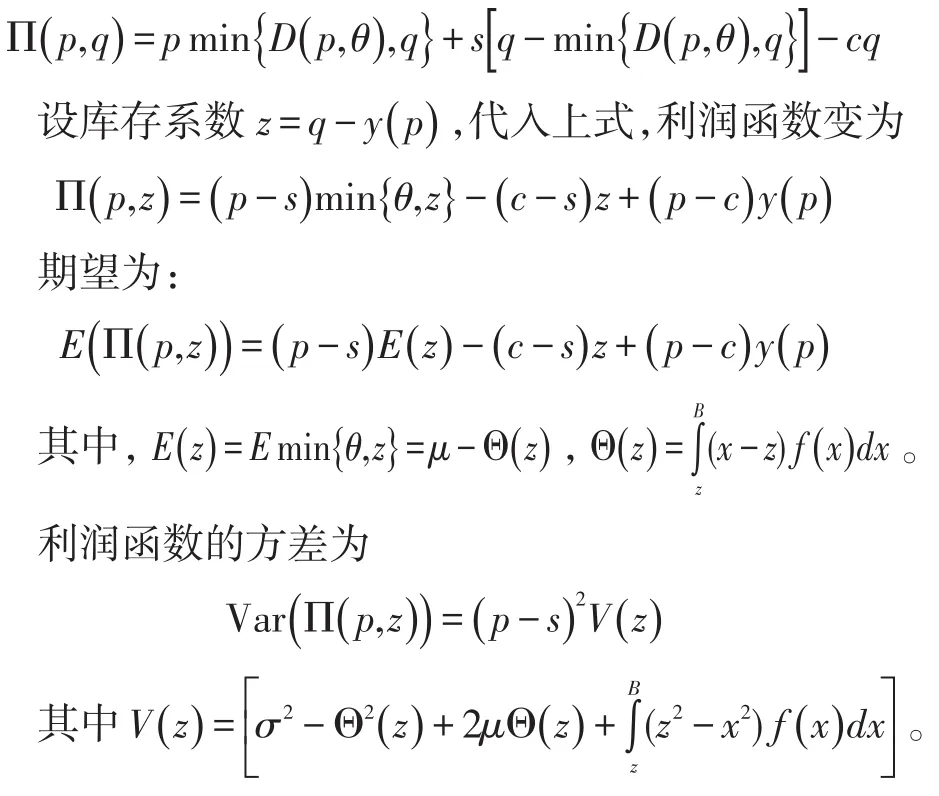
函数Θ(z)是期望存货剩余量函数，E(z)是期望销售量函数。V(z)是利润函数方差中与z相关的部分，或者由于z与p的可分离性，在利润函数的方差中剔除p后的变动部分。

对于综合报童期望利润及利润方差的目标函数，我们采用文献[11]的形式，即两者的线性和，如下：

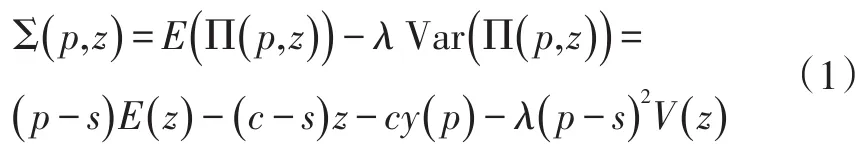
式中λ是风险系数，为利润方差赋予的权重。由于本文仅考虑风险厌恶型报童，所以λ＞0。这意味着λ越大，报童对收益的波动性越敏感，越倾向于减少波动。

将确定性需求函数y()p=a-bp代入式（1），将目标函数进一步明确为：

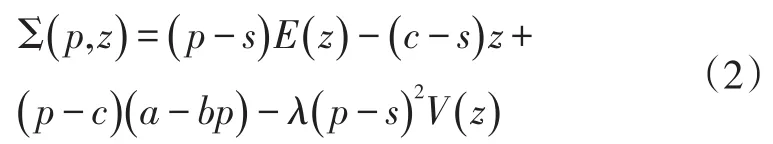
3 顺序优化

顺序优化适于特定的情景，如文献[18]所描述的两种情景：公司内的销售营销部门在给定库存水平z的情况下进行价格p(z)决策，然后生产运营部门在已知p(z)的情况下进行库存水平的决策；或者与此过程相反，先由生产运营部门在给定价格p情况下进行库存水平z(p)决策，然后由销售营销部门进行定价决策。

在进行分析前，需先做如下假设：

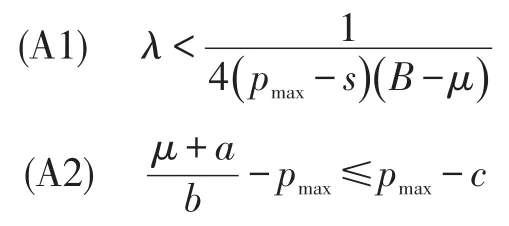
(A1)意味着，对于风险厌恶型报童来说，其对风险（方差）的加权系数有一个限度，不能无限大。因为那样地话，将导致方差权重过大，在决策时过度考虑风险因素，而对期望利润的考虑过轻。根据2.1部分的分析，(A2)意味着严格限制意义下的价格最大值与期望概念下价格最大值的距离要小于与成本的距离。

3.1 顺序优化I

顺序优化也可以分为两种情景：情景I先由生产运营部门确定库存水平z再由销售营销部门确定价格p；情景II先由销售营销部门确定价格p再由生产运营部门确定库存水平z。

对于情景I，销售营销部门在z确定的情况下进行价格p决策。其一阶条件为

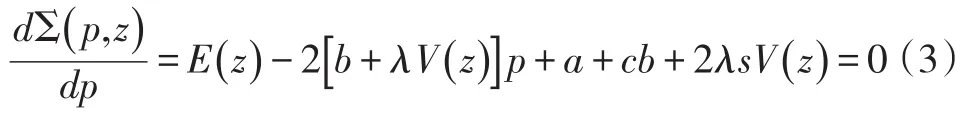
其二阶条件可以保证目标函数Σ是关于z的凹函数。所以可得最优解p：

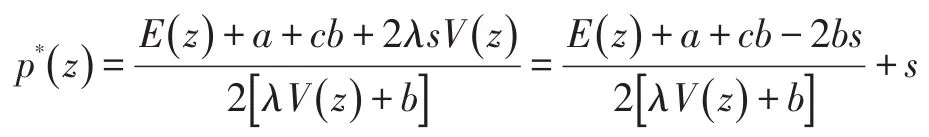
引理1：p*(z)是z的增函数；对于 ∀z∈[A,B]，有p*(z)∈[c,pmax]。

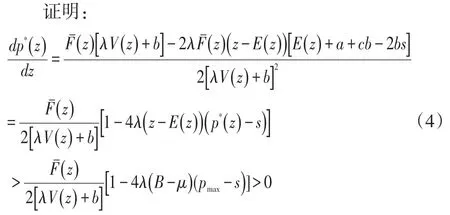
对于第二部分，

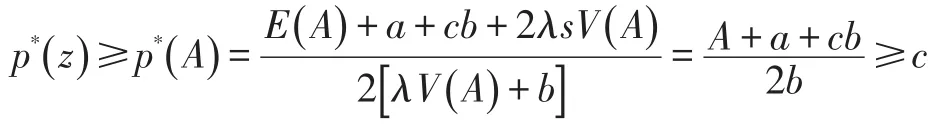
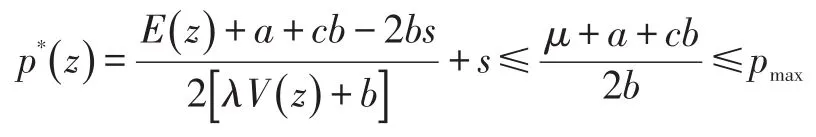
第一个不等式是分子、分母分别取其可能的最大、最小值得到，第二个不等式是由假设(A2)得到。

可见，报童的风险系数λ越小，剩余库存对于报童的决策影响越小，报童越倾向于在最优解处采取高价格。剩余库存单价越高，报童越能容忍更多的剩余库存量，就越倾向于在最优解处采取更高的价格。

接着研究z对目标函数的影响，得目标函数对z的一阶条件：

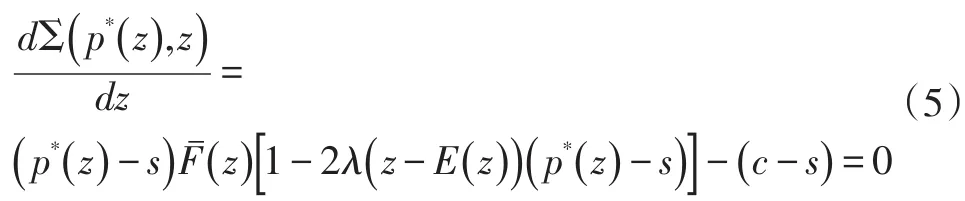
还需检验关于z的二阶条件，如文献[11]和[18]，先定义一个概念—销售损失率对价格弹性。

定义：根据经济学弹性概念的一般定义，对于给定库存水平q的情况下，销售损失率对价格弹性为：

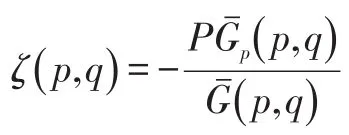
将上式代入销售损失率对价格的弹性表达式，可得：

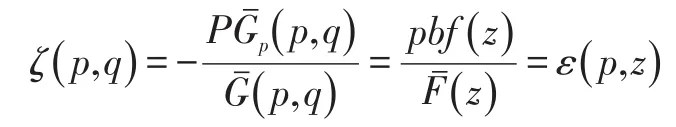
在本文中，由于考虑到处理剩余库存的单价，我们将销售损失率对价格的弹性定义为对“绝对价格”即=p-s的弹性，则上式变为：

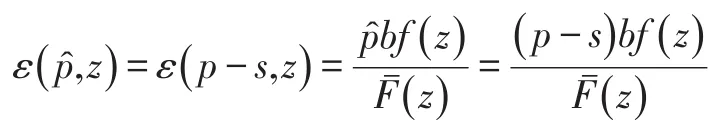
将在最优点p*()z处的弹性表示为：

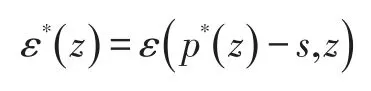
然后，有以下定理：

证明：

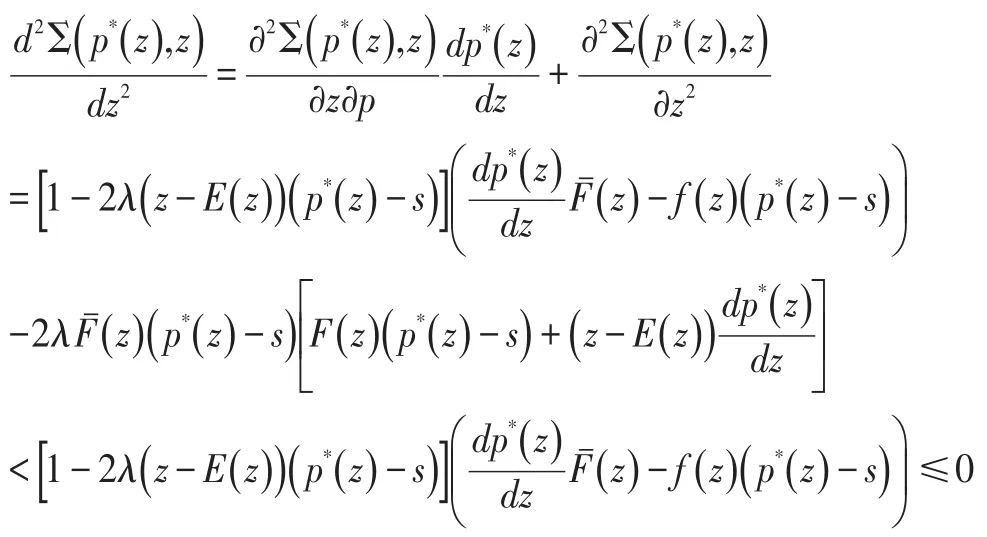
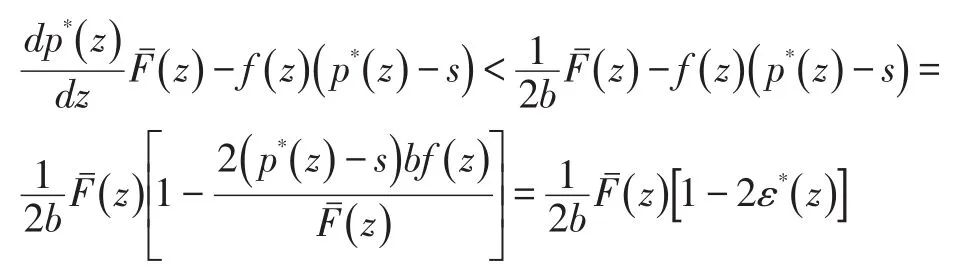
对z*关于两个重要参数λ和s的关系，有如下引理：

引理3：z*关于λ单调减；z*关于s单调增。

根据式（5）应用隐函数定理，可以分别求解z*关于λ和s的导数，易证。

3.2 顺序优化II

再分析顺序优化情景II：先确定价格p再确定库存水平z。其决策过程仍是逆向归纳求解：生产经营部门先对库存水平z进行优化，然后销售和营销部门在已知z为p函数的情况下进行定价p的优化。

生产经营部门的库存水平优化，得到目标函数关于z的一阶条件：

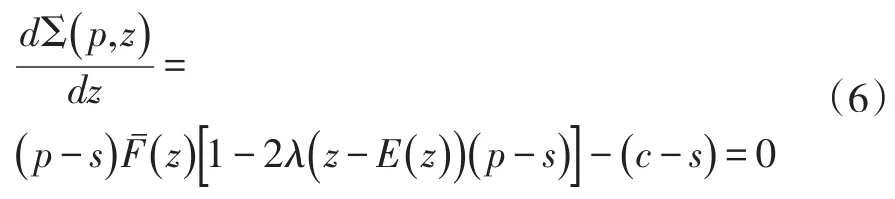
式（6）与式（5）形式相同，只是p的取值有差异。利用假设(A1)，容易验证二阶条件成立，确保了一阶条件可以获得最优解z*()p。与定理1相比，本例最优解的存在条件相对来说要宽松一些。

根据一阶条件式（5）和隐函数定理分析z与p、λ及s的关系。

引理4：最优解z*关于p单调增；关于λ单调减；关于s单调增。

证明过程同引理3。

虽然我们不能得到z*关于p的解析解，但仍可以将其视为p的函数，利用莱布尼茨链式求导法则求解目标函数对p的一阶和二阶导数。目标函数关于p的一阶条件为

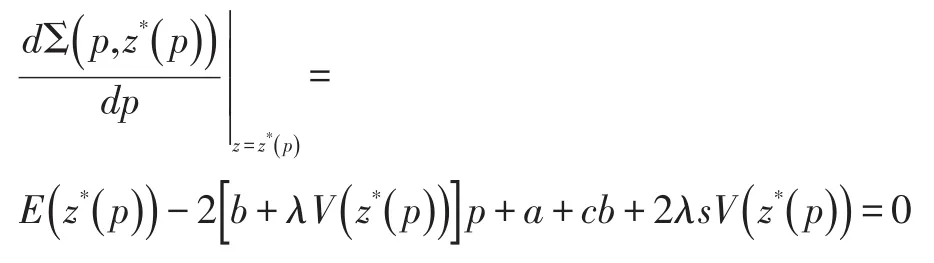
证明：p的二阶条件为：

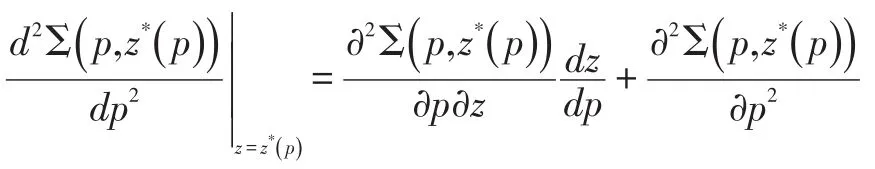
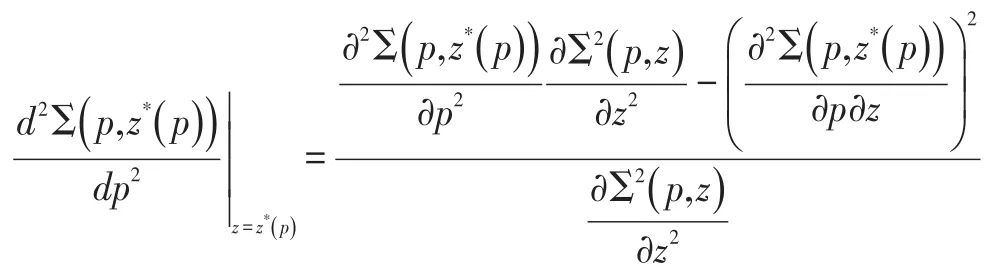
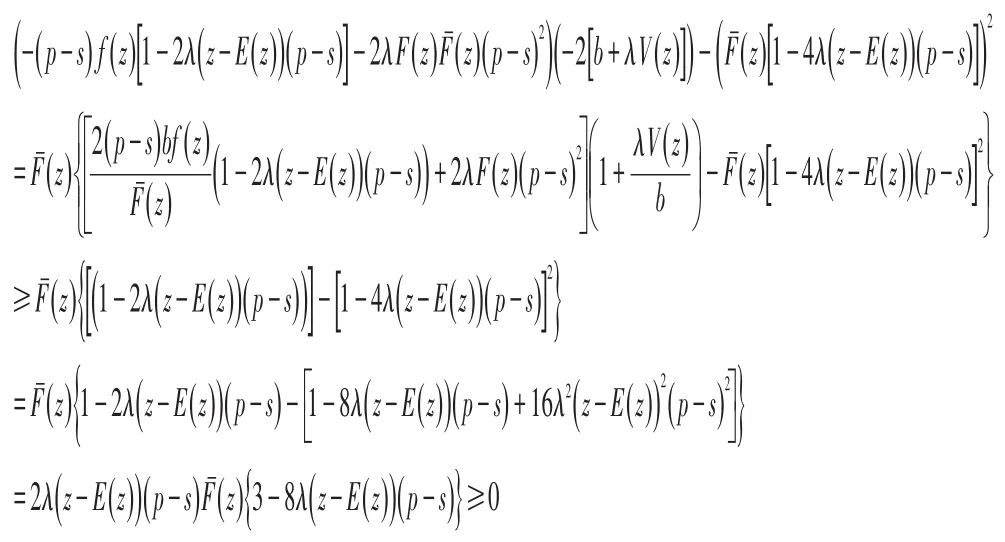
关于p*与参数λ和s的关系，有以下引理：

引理5：最优解p*关于λ单调减；关于s单调增。

证明过程同引理3、4。

比较顺序优化II的引理4和顺序优化I的引理1、3，两种情况下的最优值z*与p、λ和s的相关关系完全一致。再比较顺序优化II的引理5与顺序优化I的引理2，两种情况下的最优值p*与λ和s的相关关系完全一致。如前面所述，这绝非偶然。因为两种情况的最优解是相同的，均是目标函数相对于p和z的一阶条件组成的方程组的解。

4 同时优化

根据多变量最优化问题理论，同时优化的最优解也是由各变量的一阶条件组成的方程组的解。不过，最优解的存在需要检验海塞矩阵，根据海塞矩阵的正定性有定理3和4。

证明：需证明在点(p*,z*)处，海塞矩阵为半负定。即

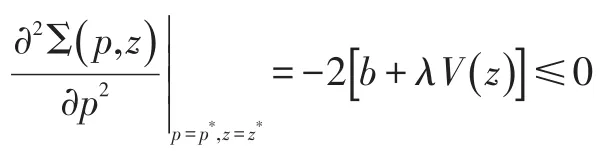
同时关于z的二阶偏导：

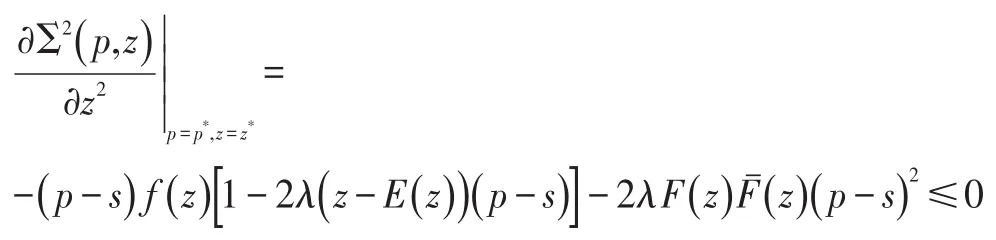
上式不等式成立是由于假设(A1)。

然后海塞行列式的值为：

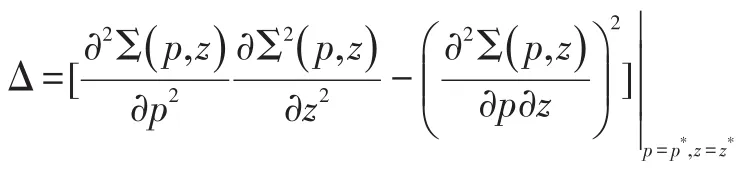
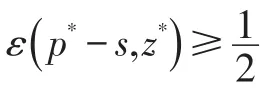
证明：需证明海塞矩阵负定，其过程与定理3完全相同，区别仅为相应的二阶偏导数及海塞矩阵行列式值的取值点，本例中为任意点(p,z)而非驻点(p*,z*)。证毕。

为了便于比较几种情况下的优化，将定理1—4的条件和结论予以总结，见表1。

由表1，定理1和2的充分条件介于定理3和4之间，强于定理3但弱于定理4。从这个角度，可以把顺序优化的最优解称为“偏全局最优解”，顺序优化I为“偏z全局最优解”，顺序优化II为“偏p全局最优解”。本质上，四个定理得到的最优解是相同的。只是定理1和定理2给出了该方程组的求解方法—代入消元法，定理1是先用函数p*(z)消去p得到z的值，然后代入p*(z)得到p；定理2是先用函数z*(p)消去z求解p，然后代入z*(p)得到z。定理3和4只是列出方程组，指出方程组的解即为最优解，并未指出求解方法。

根据此处对三种方法、四个定理最优点的比较分析，可知前面引理1和2的结论具有通用性。所以，同时优化的最优解(p*,z*)对相关参数λ和s的关系同引理1和2，此处不再赘述。

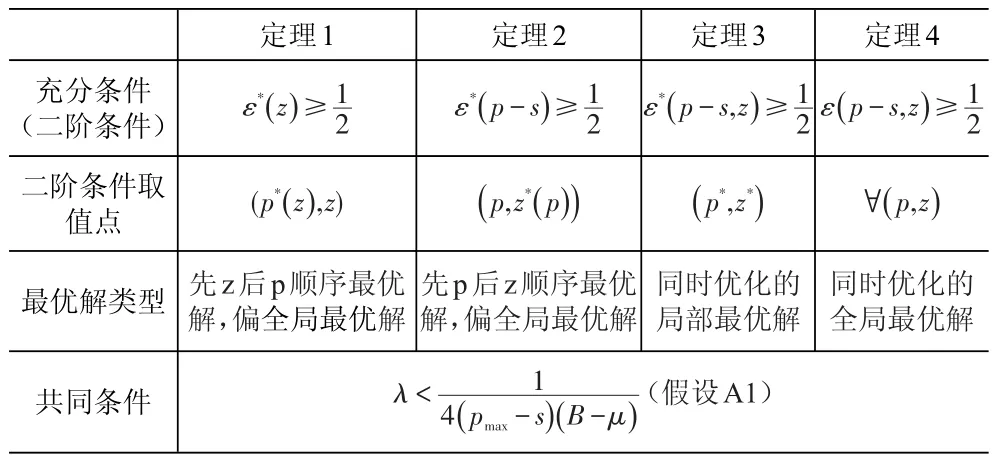
表1 顺序优化和同时优化条件及结论

5 总结

本文研究了以包含收益波动的收益函数为目标函数、以价格和库存为决策变量的报童问题，其中包含随机因素的需求函数是加法形式的显函数。论文先对这种研究思路与以往以期望收益（成本）为目标函数的区别与联系进行了分析，然后对文献[11]进行扩展，在报童收益中增加了剩余库存价值，针对风险厌恶型报童分析了顺序优化和同时优化的最优解、最优解相对于主要参数的比较静态分析以及最优解存在的充分条件，并对其实际意义进行了解释。由于需求函数的显式性，得到一些相对较明确的结论，但由于随机因素的概率密度函数和累计概率函数以隐函数形式给出，所以最优解的明确性并不彻底。幸运的是，最优解对主要参数的比较静态分析的方向性关系还是明确的。本文在研究上进行了拓展和深入，在对顺序优化和同时优化进行分析时，特别是两种情景的顺序优化，都应用了最优解求解—最优解对主要参数λ、s（另有p对z，或z对p）的比较静态分析—二阶条件判断的分析框架一以贯之，用统一的框架较清晰、系统地开展了相应研究。最后，通过对顺序优化和同时优化两种方法的比较分析，得到两种方法间的本质区别与联系：顺序优化是同时优化的局部最优解，两者的最优解及最优解的比较静态分析结论是一致的，但二阶判断条件不同，顺序优化存在性条件的复杂性介于同时优化的局部最优和全局最优之间，相当于“偏全局最优”。此外，对于风险偏好型报童，最优解及比较静态分析与风险厌恶相同或相似，但最优解成立的充分条件—二阶条件相对更为复杂，也可以得到与风险厌恶型报童相对应的二阶条件。但由于该条件无论从形式上还是实际意义上，都不如风险厌恶型报童情景中表现得简洁直观，所以本文不再对风险偏好报童的情形进行讨论。此外，在目标函数中考虑收益波动性的报童问题这一方向还有不少问题有待研究，如在需求函数方面，对于常见的乘法形式和指数形式等函数形式对问题的影响；在波动性方面，将测度波动性的常用工具变异系数融入报童模型，研究衡量波动性对决策的影响等，都是在这个方向上值得深入思考和进一步研究的问题。

[1]Petruzzi N,Dada M.Pricing and the News Vendor Problem:a Review with Extensions[J].OperationsResearch,1999,47(2):183-194.

[2]Qin Y,Wang R,Vakharia A,et al.The newsvendor problem:Review and directions for future research[J].European Journal of Operational Research,2011,213(2):361-374.

[3]Xu M,Chen Y,Xu X.The effect of demand uncertainty in a price-setting newsvendor model[J].European Journal of Operational Research,2011,207(2):946-957.

[4]Xu M,Lu Y.The effect of supply uncertainty in price-setting newsvendor models[J].European Journal of Operational Research,2013,227(3):423-433.

[5]Dogan A.Production and pricing policies in dual sourcing supply chains[J].Transportation Research Part E Logistics&Transportation Review,2015,76:1-12.

[6]Jadidi O,Taghipour S,Zolfaghari S.A two-price policy for a newsvendor product supply chain with time and price sensitive demand[J].European Journal of Operational Research,2016,253(1):132-143.

[7]Khouja M.Forward-buying and the naive newsvendor[J].Operations Research Letters,2016,44(2):238-242.

[8]Gerchak Y,Mossman D.On the Effect of Demand Randomness on Inventories and Costs[J].Operations Research,1992,40(4):804-807.

[9]Chua G,Liu Y.On the Effect of Demand Randomness on Inventory,Price and Profit[J].Operations Research Letters,2015,43(5):514-518.

[10]丁小东,徐菱,蒋葛夫,等.考虑浪费规避偏差和缺货规避偏差的零售商订购行为[J].计算机集成制造系统,2014,20(10):2 582-2 598.

[11]Javier R,Melike B,Anna J.A price-setting newsvendor problem under mean-variance criteria[J].European Journal of Operational Research,2015,247(2):575-587.

[12]杰克·韦尔奇,苏茜·韦尔奇.赢[M].北京:中信出版社,2013.

[13]叶飞,林强,李怡娜.基于CVaR的“公司＋农户”型订单供应链协调契约机制[J].系统工程理论与实践,2011,31(3):450-460.

[14]朱传波,季建华,包兴.供应风险规避下基于VaR的零售商订货策略[J].系统管理学报,2014,23(6):861-866.

[15]程露,万仲平,侯阔林,蒋威.CVaR准则下的双层报童问题模型研究[J].运筹学学报,2008,12(4):83-93.

[16]许明辉,于刚,张汉勤.带有缺货惩罚的报童模型中的CVaR研究[J].系统工程理论与实践,2006,(10):1-8.

[17]冯艳刚,吴军.突发事件环境下风险厌恶型报童博弈模型[J].系统工程理论与实践,2015,35(3):598-607.

[18]Kocabiyikoglu A,Popescu I.An Elasticity Approach to the Newsvendor with Price-Sensitive Demand[J].Operations Research,2011,59(2):301-312.

Study on Risk Aversive Newsboy Problem Considering Earnings Fluctuation

Tian Zhiyong,Zhou Li,Yuan Ruiping
(School of Informaiton,Beijing Wuzi University,Beijing 101149,China)

In this paper,targeting at the fluctuation of the newsboy earnings,we built the risk aversive newsboy model with singlephased additive stochastic demand function and price and inventory as the decision-making variables.We analyzed the model respectively through sequential optimization and simultaneous optimization,investigated the relationship between the optimal solution of the model and such parameters as risk coefficient and disposal unit price of the residual inventory,etc.,and used the concept of elasticity to describe the condition of existence and practical significance of the optimal solution of the model.Through the analysis,we found that the optimal solutions yielded by both methods were of the same nature,in that both the price and the inventory quantity were decreasing function to the risk coefficient and increasing function to the disposal unit price of the residual inventory.As for the condition of existence of the optimal solution,the local optimal solution through simultaneous optimization was the least stringent in prerequisite,followed by the optimal solution through sequential optimization,and further followed by the global optimal solution through simultaneous optimization.

newsboy model;earnings fluctuation;risk aversive;elasticity

F224.0

A

1005-152X(2017)07-0066-06

10.3969/j.issn.1005-152X.2017.07.015

2017-05-06

国家自然科学基金资助项目(71501015)；北京智能物流系统协同创新中心；智能物流系统北京市重点实验室(BZ0211)

田志勇，男，北京物资学院信息学院副教授，博士，研究方向：低碳物流、电子商务。