高阶色散对高斯脉冲在超常介质中传输的影响及色散的补偿

徐正国,薛燕陵

(华东师范大学通信工程系,上海200241)

高阶色散对高斯脉冲在超常介质中传输的影响及色散的补偿

徐正国,薛燕陵

(华东师范大学通信工程系,上海200241)

文中对超常介质和一些常规介质中色散系数进行了对比研究,发现超常介质中的各阶色散系数大于常规介质的色散系数大约3个数量级,也即在信号的传输过程中不再能忽略高阶色散的影响.基于非线性薛定谔方程,研究了高斯脉冲在超常介质中传输及各阶色散对脉冲形状的影响.发现在常规超常介质中三阶色散所致脉冲分裂是一个非常严重的问题.通过调整超常介质的结构参数,找到了既可使二阶色散得以补偿、又可使得高斯脉冲传输120 km而不出现分裂的真正可用于通信的情形.

超常介质;色散;非线性薛定谔方程;高斯脉冲;色散补偿

0 引言

至2000年第一块超常材料(Metamaterials,MMs)被Smith[1]等人在实验室制备出来以来,由于它具备负的折射率[2]、负的Goos-H¨anche位移[3]、逆多普勒效应等反常物理特性[4],越来越多的目光投向了对超常介质的物理性质和潜在应用的研究[5].随着越来越多的线性和非线性超常介质被发明,加速了对电磁波在超常介质中传输的研究[5].这些研究表明了超常介质具有正折射率区(Positive-Index Region,PIR),吸收区和负折射率区(Negative-Index Region,NIR)[6-7].Wen[8]等人利用Drude模型推导了光脉冲在超常介质中传输的非线性薛定谔方程(Non-Linear Schrodinger Equation,NLSE).而Joseph和Porsezian[9]则利用前者推导的非线性薛定谔方程研究了光脉冲传输的动力学行为.对于超常介质非线性性质的研究则更多,如自相位调制(Self-Phase Modulation,SPM)、自陡峭(Self-Steepening,SS)[10-14]等等.尽管有许许多多学者对超常介质中不同特性的研究,但是对于超常介质,尤其是负折射率材料中高阶色散对于高斯脉冲传输特性影响的研究仍然很少.本文中,我们将深入地讨论高阶色散对脉冲传输的影响.并结合分析结果进一步进行了色散补偿的研究.

在常规介质中,往往只考虑二阶色散对群速色散(Group Velocity Dispersion,GVD)效应的影响.超常介质作为一种人工合成材料,我们发现其中的各阶色散系数在数量级上高于常规介质中相应的色散系数(本文第2节),这使得在光脉冲传输中不再能忽略高阶色散的影响.本文将讨论超常介质中三阶色散和四阶色散对高斯脉冲传输的影响,分析脉冲畸变与色散之间的关系,这一工作对于了解色散的影响以及对色散进行补偿有一定的实际意义.

1 光脉冲在超常介质中传输模型

光作为一种电磁波,在超常介质中传输遵循麦克斯韦方程组,所以基于麦克斯韦方程组可以推导得到脉冲在非线性色散超常介质中的波动方程

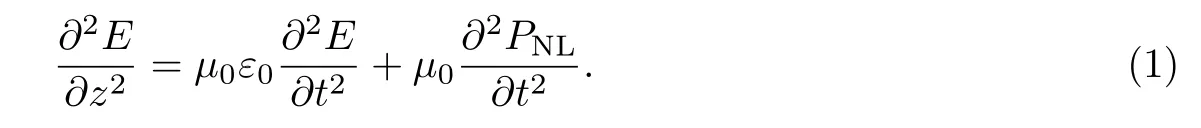
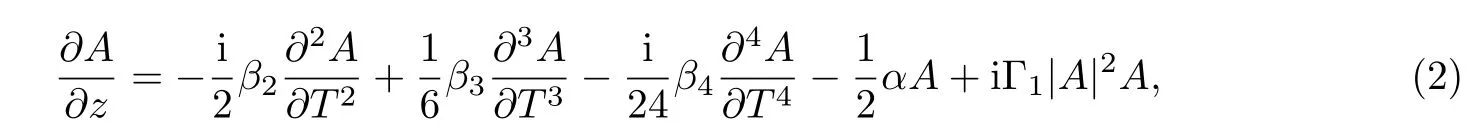
其中α为损耗系数.第i阶色散系数βi和三阶非线性系数Γ1可以分别表示为

其中χ(3)代表三阶电极化率.

超常介质中,相对介电常数εr和相对磁导率µr的频率色散关系一般都采用具有损耗的Drude模型来表示.损耗出现在Drude模型的虚部,主要影响脉冲的强度,对色散本身并没有太大的影响.因此,为了简化计算,本文忽略了损耗,也就有传播方程(式(2))中的α=0. Drude模型可以表达为

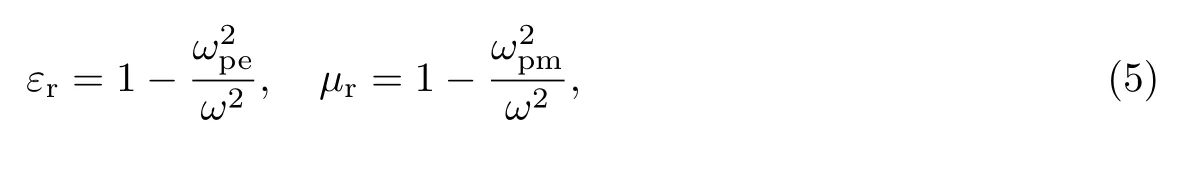
其中,ωpe和ωpm分别代表电场和磁场的等离子频率,ω代表介质中光波的中心频率.根据折射率定义由式(3)可得一阶色散、二阶色散(群速度色散GVD)、三阶色散β3(TOD)、四阶色散β4为

2 超常介质中的色散系数和非线性系数

根据色散公式(6)和三阶非线性系数公式(7)可以画出色散系数和非线性系数关于归一化频率的变化图(图1).图1中取三阶电极化率χ(3)为1.9×10−9W−1,ωpe为1.367 3×1016Hz,为0.8.

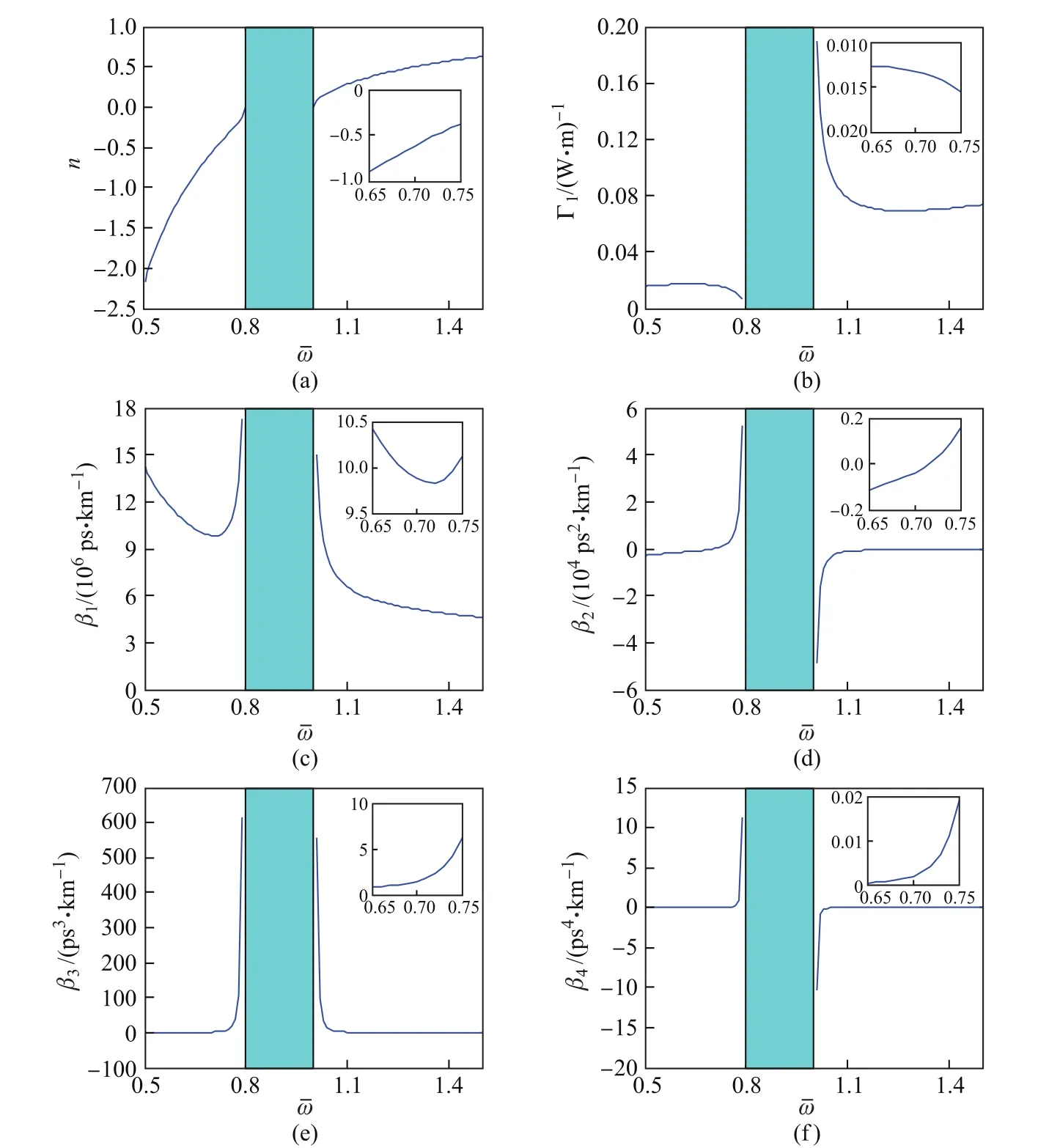
图1 折射率n、三阶非线性系数和一阶、二阶、三阶、四阶色散系数分别随归一化频率ω的变化曲线Fig.1 Variations of refractive index,third-order nonlinear coeffi cient,first-order, second-order,third-order,and forth-order depression on

图2 (a)、(c)分别为几种常规介质的二阶色散和三阶色散随波长变化的曲线图;(b)、(d)为相应的二阶色散和三阶色散随归一化频率变化的曲线图Fig.2(a),(c)Second-order and third-order dispersion in several conventional media;(b),(d) The corresponding relationship of(a),(c)with normalized frequency

图2(a)、图2(c)取自网络[15-16],展现了四种常规介质的β2和β3关于波长的变化曲线,将图2(a)、图2(c)中的横坐标改为频率并以ωpe归一化,并将纵坐标的单位分别化成ps2/km、ps3/km以便与图1(d)、图1(e)一致,可以分别得到图2(a)、图2(c)中四种常规介质的色散系数β2和β3关于归一化频率的变化曲线(图2(b)、图2(d)).从图2(b)中可以看出:四种常规的二阶色散系数β2都为负,它们都随归一化频率的增大而减小;并且它们的值都非常小,只有10−1量级.而在图1(d)中零色散归一化频率=0.706 844附近二阶色散β2的值为104量级.虽然图2(b)与图1(d)中横坐标的频率范围有一定的差距,但若按照图2(b)中曲线的趋势进行延伸,至时,|β2|也还是应该比图1(d)的情形小.所以,超常介质中的二阶色散|β2|比四种常规介质的|β2|大105量级,虽然图1(d)中β2的符号有正有负.同样,从图2(d)中可以看出:四种常规介质的三阶色散β3也都为负,它们也都随着归一化频率的增大而减小;并且它们的值都非常小,只有10−4量级.而在图1(e)中,附近三阶色散β3的值为个位数.虽然图2(d)与图1(e)中横坐标的频率范围有一定的差距,但若按照图2(d)中曲线的趋势进行延伸,至时,|β3|也还是应该比图1(e)的情形小.所以,超常介质中的三阶色散|β3|比四种常规介质的|β3|大107量级,且符号相反.我们没有查到四阶色散的数据,但据此类推超常介质中的四阶色散应该也比一些常规介质大.鉴于此,在超常介质中我们有必要充分研究超常介质中高阶色散的影响.

3 脉冲在超常介质中的传输

本文采用BPM(Beam Propagation Method)(光束传播法)进行脉冲传输仿真.入射脉冲采用具有归一化强度的高斯脉冲U(0,T)=exp,T0为脉冲在光强度峰值的1/e处半宽度.仿真中,取半极大全宽度TFWHM=5 ps,此时传输比特率为L=200 Gb/s.根据定义,二阶色散长度为LD=三阶色散长度为

3.1 同时考虑β2、β3对脉冲传输的影响

3.1.1 β2=0时,β3对脉冲传输的影响

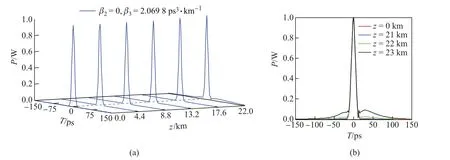
图3 (a)当β2=0,β3=2.069 8 ps3·km-1时,高斯脉冲沿超常介质z方向的传输图;(b)高斯脉冲在0 km、21 km、22 km、23 km处的波形对比图Fig.3(a)Gaussian pulse propagation whenβ2=0,β3=2.069 8 ps3·km-1;(b)Comparison of pulse waveforms at 0 km、21 km、22 km、23 km

从图3(a)可以看出,脉冲在出现分裂前(z≤22 km)始终保持入射时的形状,未有展宽.而当脉冲传输了约22 km,由于β3的作用,脉冲尾部略有抬起,并开始出现一个分裂峰.根据图3(b)中脉冲在z=0 km、21 km、22 km、23 km处脉冲波形的对比图,可以清晰地看出,尽管脉冲在传输了22 km时,脉冲分裂刚刚开始,但是当脉冲继续多传输1 km至z= 23 km,脉冲后沿却出现了非常明显的分裂峰.图3说明,虽然三阶色散长度为= 60.39 km,但这并不意味着脉冲要传输到60.39 km附近才会有β3的影响.实际情况是,在z= 23 km时,β3已经开始起作用.当脉冲传输到60.39 km,β3对脉冲的影响已经十分剧烈,甚至已经完全破坏了脉冲原有的形状.我们在分析图2时指出过超常介质中的β3至少比四种常规介质的β3大4个数量级,正是超常介质中超大的三阶色散使得高斯脉冲仅仅传输了23 km就开始出现了脉冲分裂.这也说明,虽然在零色散归一化频率有着理想的β2=0,但强烈的β3却使得实际有效传输距离很短,无法实用.因此,我们需要转换视角,考虑β3很小,但β2可以被补偿的情形.我们先考虑负折射率材料在零色散归一化频率附近的情形.

3.1.2 零色散归一化频率左侧,当β2＜0且β3＞0,β2、β3对脉冲传输的影响

表1 β2＜0且|β2|逐渐增大但β3变化很小的色散数据Tab.1 Two sets of dispersion data withβ2＜0

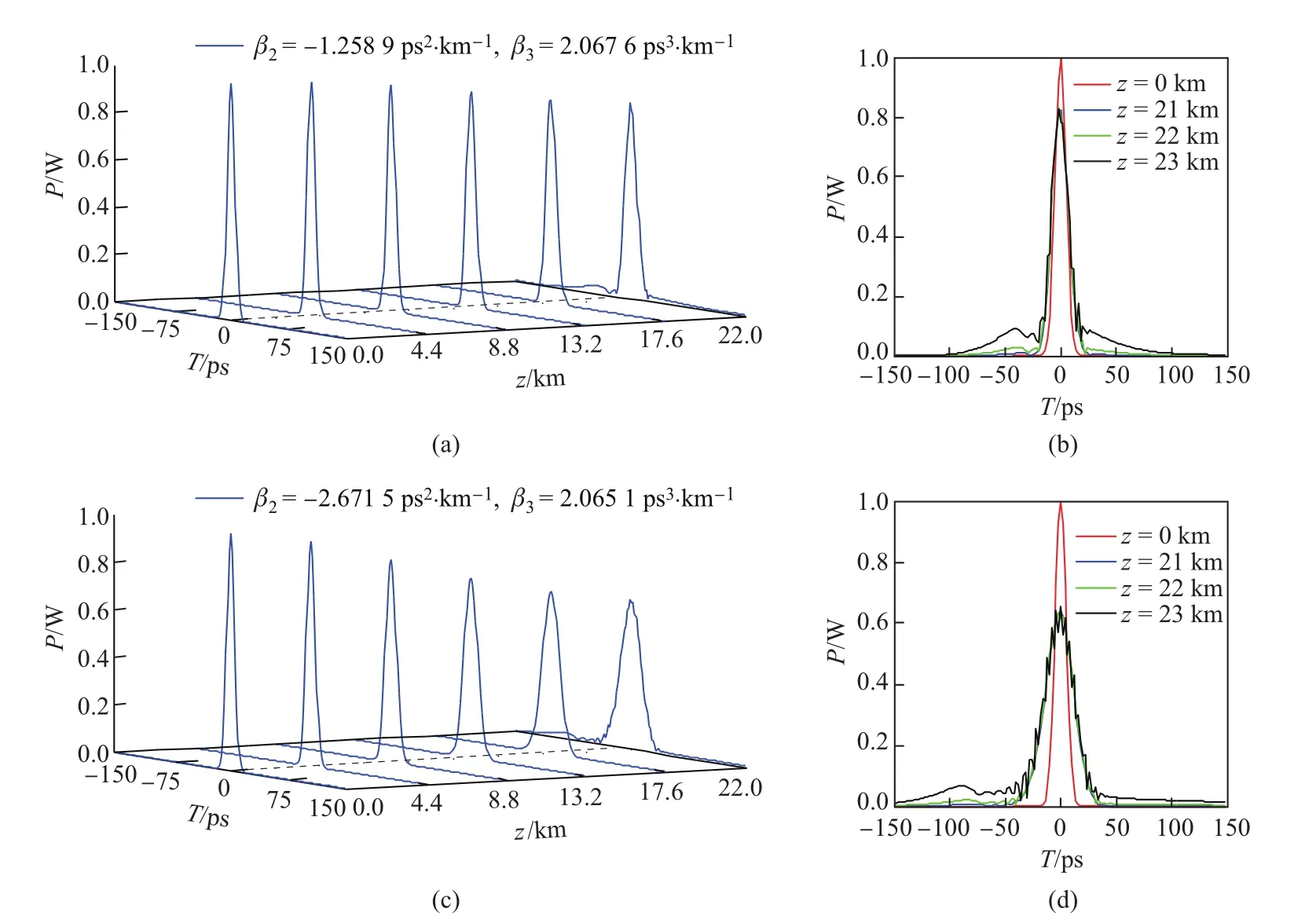
图4 (a)、(c)相应于表1中两种情况的高斯脉冲传输图;(b)、(d)为相应的脉冲在不同传输距离的波形对比图Fig.4(a),(c)Pulse propagation for two cases in Table1;(b),(d)Corresponding waveform comparison at diff erent propagation distances

从图4(b)、图4(d)可以看出,脉冲在22 km处开始出现分裂.但当脉冲出现分裂后,脉冲继续传输很短距离,脉冲就会迅速变坏,次峰峰值和宽度都会迅速增大.同样的,在上述两种情况下,三阶色散长度也都超过了60 km,但是脉冲分裂都在大约22 km处开始出现,随着脉冲的继续传输,其分裂会越来越严重,最终脉冲形状会被完全破坏.比较图4(b)与图4(d)可以发现,如果β3大小相近,当|β2|较大时,脉冲分裂出的次峰的位置相对|β2|较小时候偏离主峰更远,且次峰峰值相对小些,所以|β2|在一定程度上对脉冲分裂有抑制作用.此外,还可以看出:当β2＜0时,脉冲分裂出的次峰出现在脉冲前沿.

比较图3和图4(d)可以看出,图4(d)中脉冲分裂的情形没有图3严重,分裂峰的峰值略小且离脉冲主峰更远,但其实图4(d)所对应的β3要高于图3对应的β3.发生这一现象的原因在于图4(d)所对应的|β2|要大.这再一次证明了|β2|在一定程度上对脉冲分裂有抑制作用.

3.1.3 零色散归一化频率右侧,当β2＞0且β3＞0,β2、β3对脉冲传输的影响

图5 (a)、(c)相应于表2中两种情况的高斯脉冲传输图;(b)、(d)为相应的脉冲在不同传输距离的波形对比图Fig.5(a),(c)Pulse propagation for two cases in Table 2;(b),(d)Corresponding waveform comparison at diff erent propagation distances

表2 β2＞0且β2逐渐增大但β3变化很小的色散数据Tab.2 Two sets of dispersion data withβ2＞0

从图5(b)也可以看出,脉冲在22 km处开始出现分裂,脉冲继续传输很短距离,脉冲就迅速变坏,次峰峰值和宽度都会迅速增大.图5(d)中,脉冲分裂也是出现在大约22 km,但是当脉冲传输到22 km时,脉冲展宽已经很明显;与图4情况相似,虽然三阶色散长度也都超过了60 km,但是脉冲分裂都在大约22 km处开始出现.与图4中情况类似,当β3大小相近,β2越大,脉冲分裂峰的位置相对β2较小时候偏离主峰更远,且次峰峰值相对小,同样说明β2一定程度上对脉冲分裂有抑制作用.但是与图4中不同的是,当β2＞0时,脉冲分裂不再出现在脉冲前沿,而是出现在了脉冲后沿.

比较图3和图5(d)可以看出,图5(d)中脉冲分裂的情形没有图3严重,分裂峰的峰值略小且偏离脉冲主峰更远,但其实图5(d)所对应的β3要高于图3对应的β3.发生这一现象的原因同样在于图5(d)所对应的|β2|要大.这再一次证明了|β2|在一定程度上对脉冲分裂有抑制作用.

3.2 同时考虑β2、β3、β4对脉冲传输的影响

在常规介质中,由于β4非常小,它们对脉冲传输的影响可以忽略不计,所以通常情况下不予考虑.通过以上的讨论,已知在超常介质中β4要比常规介质中大一些.不过附近的β4大约处在10−3量级,比β3小三个数量级(图1(f)).可见高阶色散、诸如β4对脉冲传输的作用也是很小的.为了简单说明超常介质中β4对高斯脉冲传输的影响,根据图1取两组色散数据如表3所示.在这两组数据中,β2的符号不同,但|β2|、β3、β4的值相差很小.我们得到了图6的仿真结果.

表3 β2的符号不同,而|β2|、β3、β4的值接近相同的色散数据Tab.3 Two sets of dispersion data includingβ4

图6中红色为β2、β3同时作用下的脉冲传输图,蓝色为β2、β3、β4同时作用下的脉冲传输图.从图6(a)、图6(c)中可以看出,考虑β4与不考虑β4时,脉冲传输过程中整体变化趋势大体相同,即红线和蓝线整体上大致重叠.但当对比两者传输到21 km处放大后的细节图(图6(b)、图6(d))时可以发现,对于β2＜0和β4＞0的情况,在脉冲半高带宽处,蓝线在红线内侧,说明β2对脉冲的展宽起到一定的抑制作用;而对于β2＞0,β4＞0的情形,情况则有所不同,即蓝线出现在了红线的外侧,说明此时β4加剧了脉冲的展宽.从图6(a)、图6(c)也可以看出,β4不会对脉冲分裂位置产生影响,β2＜0时,脉冲分裂依然出现在前沿;而β2＞0时,脉冲分裂出现在后沿.

4 色散补偿

据前分析,超常介质中二阶、三阶色散都是较为严重的问题.即便是能够通过选取归一化频率使得β2=0、即完全没有二阶色散所致的脉冲展宽,但三阶色散所致的脉冲尾部震荡依然在脉冲传输了23 km时就出现了.所以应该寻找是否有二阶、三阶色散都可以得到补偿的情形或β3很小使得很长、但β2可以被补偿的情形.既然超常介质的特性依赖于系数ωpe和 ωpm,这两系数依赖于超常介质的结构,所以超常介质的所有特性都可以通过人为调节超常介质的结构去改变.如果欲使二阶、三阶色散都得以补偿,根据色散补偿理论,应有

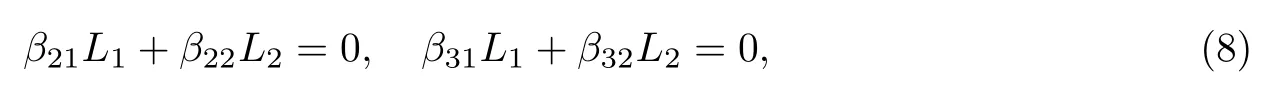
其中,L=L1+L2是色散排布周期,β2j和β3j分别是长为Lj的超常材料的二阶和三阶色散系数(j=1,2).也就是说需要找到对于同一个归一化频率β2和β3既可为正、又可为负的情形.据此要求,我们研究了超常介质特征参数对结构参数ωpe和ωpm的依赖关系.图7给出了图1中各参数对于区间0.1≤≤0.9和0≤≤2的曲面图.根据定义,和的变化即代表了ωpe和 ωpm的变化.

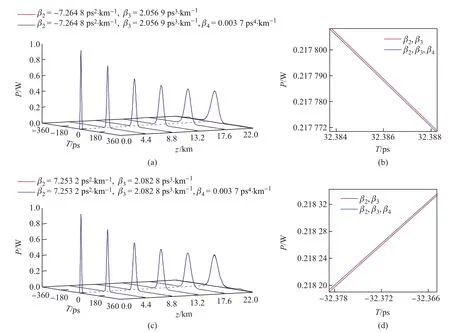
图6 (a)、(c)相应于表3中两种情况的高斯脉冲传输图,其中红线没有考虑四阶色散;(b)、(d)脉冲传输到21 km时相应的半高带宽处的局部放大图Fig.6(a),(c)Pulse propagation for two cases in Table 3 and red line is for the case without β4;(b),(d)Partial waveform magnification at FWHM for z=21 km

在图7(d)和图7(f)中β2和β4有正有负,可以根据实际需求进行取值.然而值得注意的是,图7(e)中β3在这个结构参数和归一化频率变化区域内始终为正值.也就是说,我们无法找到β3为负的值,也就无法进行三阶色散的补偿.所幸的是,我们几经搜索,找到了如表4所示的一组参数值.这组参数中,对于同一归一化频率,β2可正可负,且正值与负值非常接近,使得二阶色散几乎可以完全补偿.同时β3非常之小,以至于三阶色散长度可以接近380 km.也就是说,在二阶色散效应得以补偿之时,三阶色散效应基本上还未出现.

将表4中两种超常材料M1和M2交叉周期性排布,可以得到一个平均GVD很小甚至可以忽略的新型复合超常材料.取M1和M2的长度L1=L2=20 km(复合超常材料的周期即为L=40 km),在忽略损耗时,对高斯脉冲传输的仿真结果如图8所示.

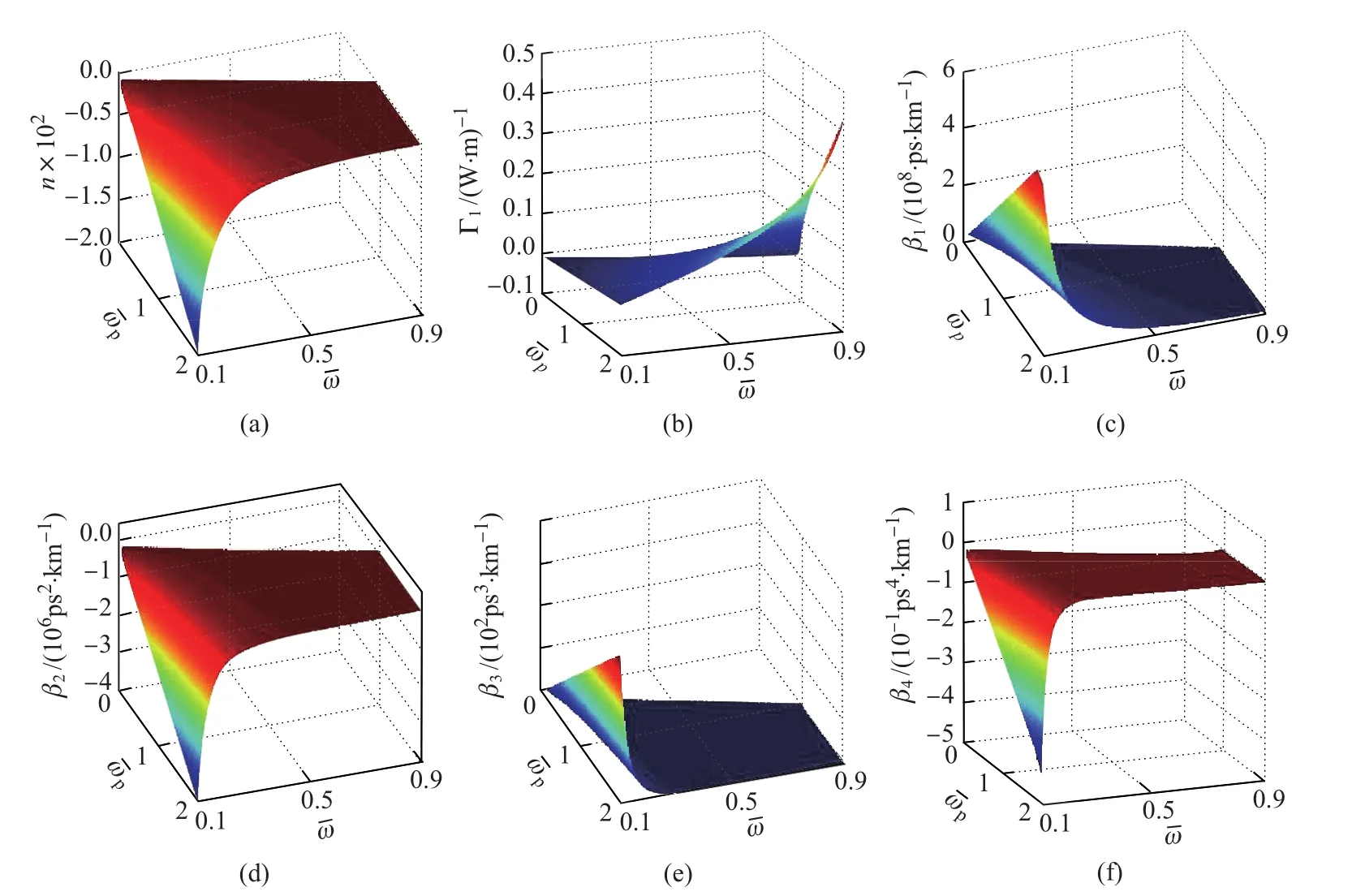
图7 折射率n、三阶非线性系数和一阶、二阶、三阶、四阶色散系数分别随归一化频率和的变化曲线Fig.7 Variations of refractive index,third-order nonlinear coeffi cient,fi rst-order, second-order,third-order,and forth-order depression onand

表4 两组β2符号相反,且|β2|接近、β3值较小色散数据Tab.4 Two sets of data with diff erentβ2

图8 (a)高斯脉冲在复合超常材料M1+M2中色散补偿后传输120 km的脉冲波形变化图; (b)为(a)的俯视图,即高斯脉冲能量扩散图Fig.8(a)Waveform variation of Gaussian pulse’120 km propagation in compound metamaterials M1+M2;(b)Top view of(a)

从图8(a)可以看出,脉冲在M1中传输时,脉冲的宽度随着传输距离增加而展宽,脉冲的幅值则因为脉冲的展宽而下降.当传输距离为L1=20 km,脉冲幅值降为0.8.此时脉冲进入M2继续传输,随着脉冲传输距离的继续增加,脉冲高度逐渐增高.而且从图8(b)也可以看出,此时脉冲的宽度也逐渐收缩,即脉冲的GVD效应得到了补偿.当脉冲传输到Z=L1+L2=40 km时,脉冲的幅值已经恢复到了入射幅值,即脉冲从宽度和幅度两个方面得到了完全补偿.此后的情况重复第一个周期的情况,脉冲周期性地被展宽与补偿,直到传输到更远的距离Z=120 km.虽然脉冲传输了一个M1+M2的周期后,β2的GVD效应得到了基本补偿,但β3的作用则仍然留存,并且随着传输距离的增加而累积.所幸的是,我们发现M1和M2的三阶色散长度都很长,接近380 km(表4).当我们的仿真距离接近140 km时,三阶色散效应刚刚开始显现,此时可以在传输链路中加装中继器对脉冲进行整形,补偿β3的作用.

5 结论

本文研究了超常材料中高阶色散与归一化频率的关系,发现超常材料的二阶色散和高阶色散与一些常规介质相比非常之大,对脉冲的传输有更为严重的影响.虽然我们找到了β2=0脉冲不会展宽的情形,但却因为β3太大致使脉冲仅仅传输了23 km就出现了分裂.通过研究超常介质色散系数与结构参数的关系,找到了β2可以被补偿且β3很小的情形,使高斯脉冲可以顺利传输120 km,说明超常介质能够用于通信.

从仿真中还可看出,|β2|不仅像已有研究指出的那样会引起脉冲的展宽,而且展宽比一些常规介质更为严重,同时β2的符号也会影响脉冲分裂出现的位置;而β3则会比某些常规介质中更为严重地影响脉冲形状,使得脉冲出现分裂峰,甚至完全破坏脉冲的完整性;β4的作用则会受到β2的符号影响,如果β2＜0,β4可抑制脉冲展宽,相反,当β2＞0,β4则加剧脉冲展宽.

[1]SIMTH D R,KROLL N.Negative refractive index in left-handed materials[J].Phys Rev Lett,2000,85(14): 2933-2936.

[2]VESELAGO V G.The electrodynamics of substances with simultaneously negative values ofµandε[J].Sov Phys Usp,1968,10(4):509-514.

[3]BERMAN P R.Goos-H¨achen shift in negatively refractive media[J].Phys Rev E,2002,66(6):067603

[4]ZHAROV A A,SHADRIVOV I V,KIVSHAR Y S.Nonlinear properties of left-handed metamaterials[J].Phys Rev Lett,2005,30(24),3356-3358

[5]LAZARIDES N,TSIRONIS G P.Coupled nonlinear Schr¨oinger fi eld equations for electromagnetic wave propagation in nonlinear left-handed materials[J].Phys Rev E,2005,71:036614.

[6]ZIOLKOWSKI R W.Superluminal transmission of information through an electromagnetic metamaterial[J]. Phys Rev E,2001,63:046604.

[7]ZIOLKOWSKI R W.Pulsed and CW Gaussian beam interactions with double negative metamaterial slabs[J]. Opt Exp,2003,11:662-681.

[8]WEN S C,XIANG Y J,DAI X Y,et al.Theoretical models for ultrashort electromagnetic pulse propagation in nonlinear metamaterials[J].Phys Rev A,2007,75:033815.

[9]JOSEPH A,PORSEZIAN K.Stability criterion for Gaussian pulse propagation through negative index materials [J].Phys Rev A,2010,81:023805.

[10]SARMA A K.Solitary wave solution to the generalized nonlinear Schr¨odinger equation for dispersive permittivity and permeability[J].Eur Phys J D,2011,62:421.

[11]SARMA A K.Modulational instability of coupled nonlinear fi eld equations for pulse propagation in a negative index material embedded into a Kerr medium[J].J Opt Soc Am B(JOSA–B),2011,28(4):944.

[12]SAHA M,SARMA A K.Modulation instability in nonlinear metamaterials induced by cubic-quantic nonlinearities and higher order dispersive eff ects[J].Opt Commn,2012,291:321-325.DOI:10.1016/j.optcom.2012.11.011.

[13]SCALORA M,SYRCHIN M S,AKOZBEK N,et al.Generalized non-linear Schr?dinger equation for dispersive susceptibility and permeability:Application to negative index materials[J].Phys Rev Lett,2005,95(1):013902.

[14]YANG R,ZHANG Y.Exact combined solitary wave solutions in nonlinear metamaterials[J].J Opt Soc Am B(JOSA–B),2011,28,123-127.

[15]THORLABS.Inc:Dispersion-compensating prism pairs for ultrafast lasers[EB/OL].[2016-04-10].https://www. thorlabschina.cn/images/TabImages/AFSprisms GVDG2-480.gif.

[16]THORLABS.Inc:Dispersion-compensating prism pairs for ultrafast lasers[EB/OL].[2016-04-10].https://www. thorlabschina.cn/images/TabImages/AFSprisms TODG2-800.gif.

(责任编辑：李艺)

Infl uence of high-order dispersions on the propagation of Gaussian pulse and the compensation of dispersion in metamaterial

XU Zheng-guo,XUE Yan-ling
(Department of Communication Engineering,East China Normal University, Shanghai 200241,China)

This paper compares the dispersion in metamaterial and in some conventional media.It is found that each order of the dispersion in metamaterial is larger in three orders of magnitude than that in conventional media,so that high-order dispersions have to be taken into consideration in the signal propagation.We analyze the impact of each order of the dispersion on the propagation of Gaussian light pulse based on the nonlinear Schr¨odinger equation and the beam propagation method(BPM).We find that third-order dispersion leads to a serious pulse splitting.A case is found in which Gaussian pulse can propagate in metamaterial to 120km without splits and second dispersion can be compensated by adjusting structure of metamaterial.This is significant to optical communications.

metamaterial;dispersion;nonlinear Schr¨odinger equation;Gaussian pulse;dispersion compensation

TN913.7

A

10.3969/j.issn.1000-5641.2017.04.011

1000-5641(2017)04-0126-13

2016-07-26

国家自然科学基金(11234003,91436211)

徐正国,男,硕士研究生,研究方向为光通信与光电子器件.E-mail：xuzg2017@163.com.

薛燕陵,女,教授,博士生导师,研究方向为光通信.E-mail：ylxue@ee.ecnu.edu.cn.