基于随机森林的犯罪风险预测模型研究

王雨晨,过仲阳,王媛媛

(华东师范大学地理科学学院,上海200241)

基于随机森林的犯罪风险预测模型研究

王雨晨,过仲阳,王媛媛

(华东师范大学地理科学学院,上海200241)

犯罪预测是犯罪预防的前提,也是公安部门亟待解决的问题.随机森林作为一种组合分类方法,具有准确率高、速度快、性能稳定的特性,且能够给出指标重要性评价,本文将其应用于犯罪风险预测中.实验证明,随机森林方法选出的指标集可以显著地提高预测准确率,基于该方法构建的预测模型相较于神经网络与支持向量机具有更高的准确性和稳定性,能够满足犯罪风险预测的需求.

随机森林;犯罪风险预测;指标集选择

0 引言

犯罪预测是实现精准、快速打击犯罪行为的前提,对于犯罪风险的准确预测可以为预防犯罪提供有效的决策信息,实现警力跟着警情走,提高警务工作效率.随着大数据与数据挖掘技术的发展,公安部门的警务大数据平台已经进入了实际应用阶段,犯罪相关数据的数量与质量也在大幅度提升,使得数据挖掘技术支撑下的犯罪预测成为可能.

目前,我国对于犯罪预测的研究多数停留在定性预测阶段,定量预测的缺少造成了犯罪预测精度较低,从而使得预测结果缺少实用价值[1].在犯罪行为的定量预测方面,通过建立数学模型进行预测的相关学习算法有:利用决策树算法对涉嫌违法犯罪人员数据进行挖掘,预测其犯罪风险[2-3];利用自回归移动平均模型、支持向量机和向量自回归模型的动态优化组合,预测立案总数的年际变化[4];利用模糊BP(Back Propagation)神经网络预测各年份公安破案的案件数量和检察院受理的案件数量[5];利用基于模糊信息粒化的支持向量机拟合犯罪时序信息[6]等.

在进行犯罪风险预测的过程中,构建模型所使用的训练数据的质量直接决定了最终预测结果的准确性,如何选择与预测结果相关的有效指标信息成为建立模型的关键.犯罪信息属性繁杂,构建模型时过多的指标容易造成预测模型的过度拟合,反而会降低实际预测时的准确性.同时,犯罪数据数量大、有噪声、不完全、模糊和随机等特点,也使得犯罪风险预测中指标集合的选择显得尤为重要.

本文介绍了一种对于数据噪声鲁棒、预测结果准确且稳定的组合分类算法——随机森林(Random Forest),应用于犯罪信息指标集合的选取与犯罪风险的预测.实验结果证明,该算法选出的指标集合具有明显的合理性,改善了指标选择缺乏客观标准的现状.同时基于该算法建立的风险预测模型在预测的准确性和稳定性方面,相较于其他模型均有一定的提升,得到了较为理想的结果.

1 基本原理

1.1 随机森林原理

随机森林是组合分类方法的一种,它由大量CART(Classifi cation And Regression Tree)决策树的集合构成,所以称之为“森林”.其中生成单棵树的训练数据由独立抽样产生,单棵树中每个内部节点的候选分裂属性从全部的候选属性中随机抽取.随机森林的最终分类结果由每棵决策树投票决定[7-8].随机森林具备以下特点:

①对于包含d个元组的原始数据集D,产生n棵决策树,迭代i(i=1,2,···,n)次利用自助法(Bootstrap)每次从数据集D中有放回地抽取d个元组作为训练集Di,每个Di都是一个自助样本.由于是有放回地随机抽样,D中的某些元组会被多次抽取,而另一些元组则不会出现在Di中.因此,未被抽取的元组可以作为检验集.

可以证明,D中每个元组被抽中的概率为1/d,因此,该元组未被抽中的概率为(1−1/d),抽取N次后某个元组未被抽中的概率为(1−1/d)N.当N足够大时, (1−1/d)N收敛于e−1=0.368.所以一般情况下,自助法产生的训练集和检验集分别占63.2%和36.8%.

②随机属性选择,对于全部F个分类属性,每个内部节点随机选择f个属性形成候选分类属性集,其中f≪F,且f的值固定.

③单棵树生成过程中完全生长,不进行剪枝操作,有助于消除树的偏移.

④分类结果由n棵决策树投票决定,每棵树Ti返回一个分类结果且有相同的投票权重,票数最多的类成为最终的分类结果.

1.2 泛化误差收敛性[9-11]

对于组合分类模型{h1(X),h2(X),···,hk(X)},其中h(X)表示一个分类器对于输入X产生相应的类标号输出,该分类器的训练样本由自助法得到.定义组合分类模型的间隔函数(Margin Function),公式为

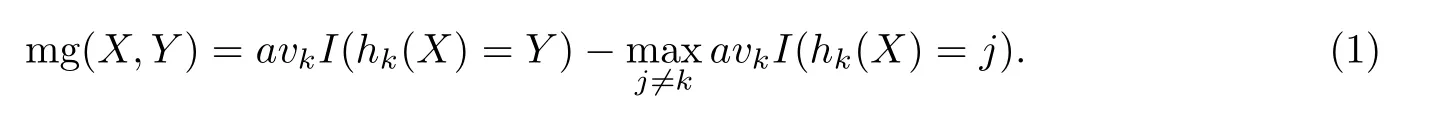
间隔函数可以衡量分类模型的正确性与确信度,该函数表示平均正确分类数与平均错误分类数的间隔程度,正确分类的数量超过错误分类的数量越多,说明分类模型的性能越好.因此,分类模型的泛化误差定义为

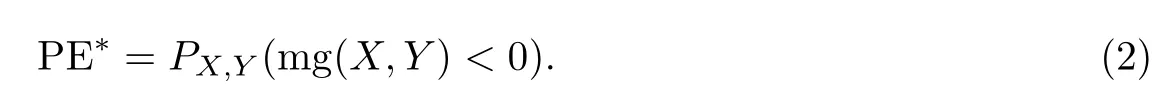
该泛化误差推广到随机森林,hk(X)=h(X,Θ),其中Θ表示单棵决策树的参数向量.随着森林中分类树数目的增加,根据大数定律,泛化误差几乎处处收敛,公式为

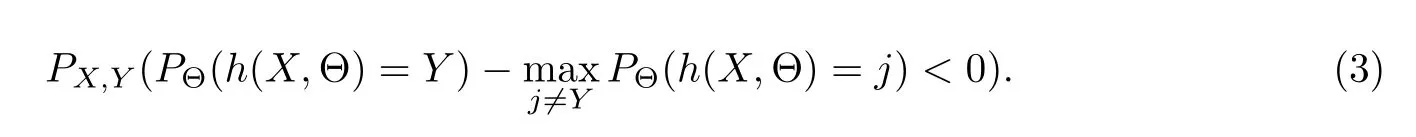
这说明,随机森林对于噪声和离群点是鲁棒的,也不会产生过度拟合问题.

1.3 OOB估计

装袋(Bagging),也叫自助聚集(Bootstrap Aggregation),属于组合分类方法.其一般过程是,通过自助法(Bootstrap)从训练集中有放回地抽取k个自助样本集,分别学习得到k个分类模型,最终聚集(Aggregate)所有模型得到装袋分类器.根据第1.1节中证明可知,每次抽取自助样本时,约36.8%的数据未被抽中,未被抽中的数据称为袋外(Out-Of-Bag,OOB)数据,构成检验集.这种使用袋外数据估计模型准确率的方法称为OOB估计[12].OOB估计可以得到分类模型的泛化误差,并且不同于交叉验证的是,此方法不需要额外的计算.实验证明, OOB误差属于无偏估计.

1.4 基于OOB估计的属性选择

随机森林衡量属性重要性的理论基础是,通过在每次迭代过程中随机置换第j个分裂属性Xj,打破其与类标号属性y的联系.当属性Xj被置换后,剩余的属性用于观测随机森林OOB估计的变化,如果属性置换后的分类准确率大幅降低,说明属性Xj与相应类标号属性y的相关性较强.平均所有树在属性Xj被置换前后分类准确率的差值作为衡量变量重要性的度量[13-15].属性Xj在第k棵数的变量重要性(Variable Importance,VI)计算公式为

根据OOB误差最小化准则,在拟合所有森林后,依据属性重要性选取其子集并检查OOB误差,选择拥有最小属性数量的方案.并且被选属性的误差率不超过所有森林最低误差的标准误差,标准误差利用二项计数误差sqrt(p(1−p)×1/N)计算得到.该方法对于高维小样本数据较为适用[16],通过此方法可以选取候选属性集的最优子集.

2 模型构建

2.1 实验数据的准备

本文的实验数据来源于某公安分局数据库中犯罪人员信息的部分记录,所有分析操作均在公安平台上进行,数据使用前已进行脱敏处理.利用犯罪人员信息挖掘得到犯罪风险预测模型,该模型的主要目的是通过犯罪人员信息分析出可能引发不同犯罪风险的各因素之间的关系,最终协助有关部门制定相应的政策,预防严重危害公共安全案件的发生.模型最终的分类结果是“犯罪程度”,包含{严重,一般}两类.

为了提高数据质量,需要对数据做预处理.首先,数据库中存在着与预测结果无关的冗余指标,如“案件编号”等,这些指标对于本文的研究没有意义,故将其删除;其次,某些指标包含了有穷多个且无序的不同值,应将其泛化到较高的概念层次,使该指标的不同值数量减少,如将信息表中的“现住址全称”泛化成“是否本区居住人口”;最后,处理信息表中的缺失值,原则是尽可能地填补缺失值,如“年龄”指标的缺失值可通过“出生日期”和“案发时间”填充,无法填充缺失值的记录做删除处理.经过数据预处理后,最终提取有效记录4 053条,其中“严重”类别1 969条,“一般”类别2 084条.提取的指标名称及编号参见表1.

表1 指标名称及编号Tab.1 ID of the variables

2.2 相关指标的确定

利用用第1.4节所介绍的方法对样本数据进行计算,得到各指标被排除后的平均OOB准确率降低值,其结果参见表2.以准确率降低程度为标准对指标进行排序,获得各指标的重要性排名,准确率降低值越大,说明该指标越重要,指标重要性降序序列为114、105、102、107、113、108、115、104、103、101、111、112、106、110、109,其结果参见图1(a).

按照图1(a)的排序结果,选择误差率满足1−S E规则的前6个指标作为候选指标集S1= {114,105,102,107,113,108}.同时,根据图1(a)的重要性排序,向候选指标集S1中逐一增加指标,使得S2=S1∪{115},S3=S2∪(104),S4=S3∪{103},得到3个新的指标集,用于对比得出OOB估计标准下的最优指标集.分别计算以上4个指标集的OOB误差率,结果为24.38%, 24.18%,23.91%和24.53%.因此选择OOB误差率最小的S3作为候选指标集.

为了进一步验证S3指标集的合理性,利用基尼指数方法再次选择指标集[17],计算各指标的平均基尼指数降低值,其结果参见表2,排序结果参见图1(b).根据图1(b)中各指标平均基尼指数降低值降序排序结果,选择基尼指数降低值较高的前8个指标形成对比指标集S5={105,110,102,114,103,104,108,107}.同时,将全部指标作为对比指标集S6.计算S5与S6两个指标集的OOB误差率分别为33.36%和41.92%.

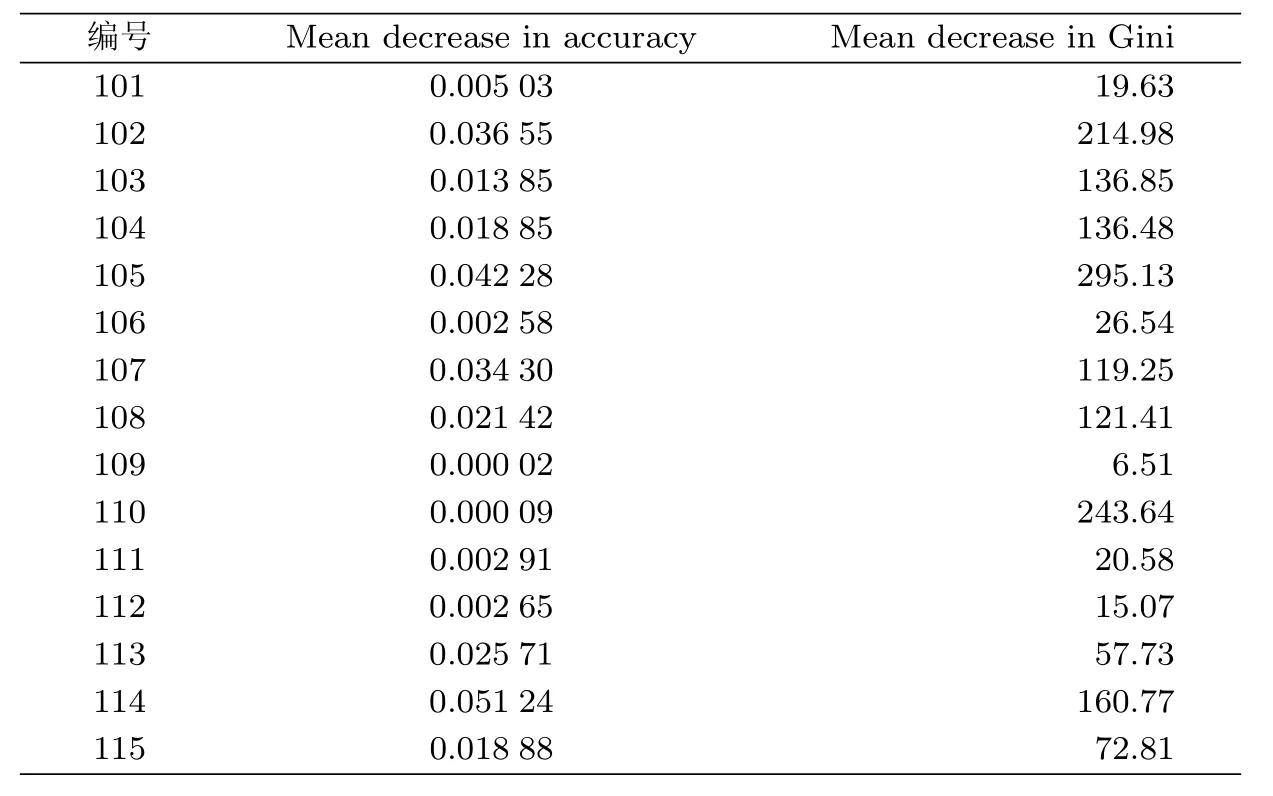
表2 指标重要性度量Tab.2 Importance of the variables using diff erent measures

图1 不同标准下的指标重要性排序Fig.1 Importance order of the variables using diff erent measure

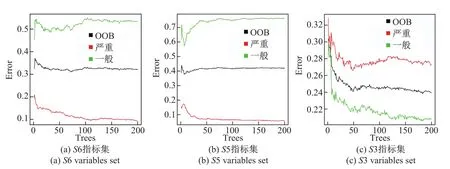
图2 不同指标集的OOB误差率Fig.2 OOB error rates of diff erent variables sets

S3、S5与S6三个指标集的OOB误差对比结果参见图2,图中体现了随着随机森林中树的棵数的增加,OOB误差率的变化趋势,其中黑色曲线表示总体的OOB误差率,红色曲线表示“严重”类别的OOB误差率,绿色曲线表示“一般”类别的OOB误差率.通过对比得出,S5与S6指标集的OOB误差率均大于S3,因此选择S3作为最终的指标集参与模型构建.

2.3 预测模型的实现

根据最终确定的S3指标集中的元素,剔除原数据中不属于S3指标集的指标列,余下的数据作为构建预测模型的数据集.分别使用神经网络、支持向量机和随机森林建立预测模型,并进行10-折交叉验证.

神经网络由相互联系的计算单元构成,每个计算单元执行两次连续的计算:输入的线性组合;对输入结果的非线性计算得到的输出值作为神经网络的下一个计算单元的输入.每个计算单元的连接都有一个相关联的权重.

支持向量机使用一种非线性映射,将原始数据映射到一个新的高维空间中,在这个新的高维空间中,有可能应用线性模型来获得一个超平面将原数据分离.原输入数据到较高维空间的非线性变换是在核函数的帮助下进行的.

为确定各模型的参数,采用控制变量法,调节3个模型的参数并观察模型行为,选择最优参数,使其预测结果达到相对较好的准确率,参数优化结果见表3.对于神经网络模型,最终确定其参数:隐藏层中的节点个数设为8,收敛过程中所允许使用的最大迭代次数设为300,反向传播算法权重的更新率设为0.01;对于支持向量机,最终确定其参数:使用高斯径向基核函数K(x,y)=exp(−∥x−y∥2×gamma),gamma值设为0.1,违反边际所引入的损失设为50;对于随机森林,最终确定其参数:森林中树的棵数设为200,每次分裂随机选择的候选变量个数设为2.

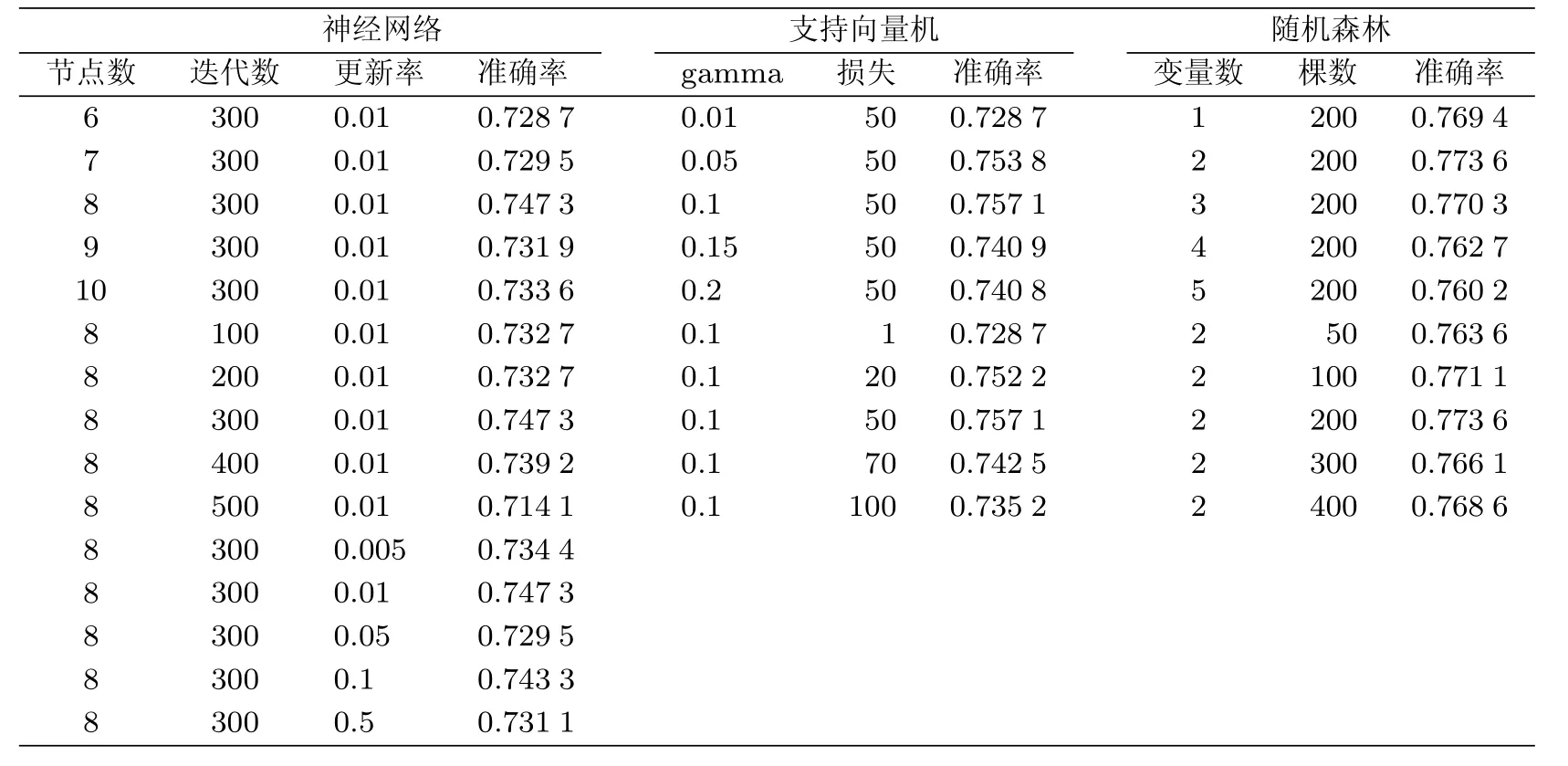
表3 各模型参数设置及相应结果Tab.3 Prediction accuracy for each model using diff erent parameters

按照优化后的参数,分别构建神经网络、支持向量机和随机森林模型,在每次迭代交叉验证完成后,计算各模型的准确率、精度与召回率.其中,准确率(Accuracy)指被正确分类的正元组和负元组占总元组的比例,衡量了预测模型的总体识别率,计算参见公式(6);精度(Precision)指被预测为正元组的元组中实际为正元组的比例,衡量了预测模型的精确性,计算参见公式(7);召回率(Recall)指实际为正元组的元组中被预测为正元组的比例,衡量了预测模型的完全性,计算参见公式(8).

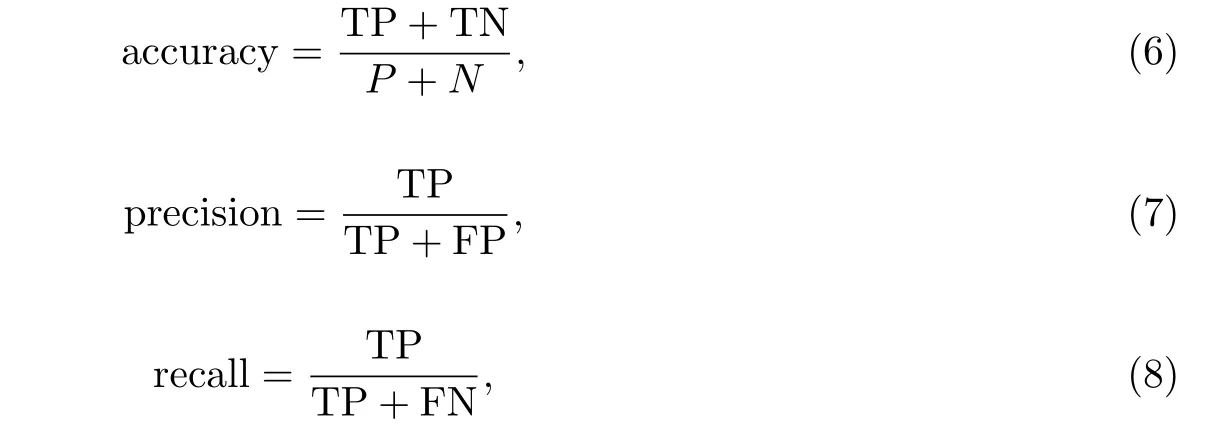
其中,P(Positive)指正元组的数量;N(Negative)指负元组的数量;TP(True Positive)指实际为正元组而被分类为正元组的数量;TN(True Negative)指实际为负元组而被分类为负元组的数量; FP(False Positive)指实际为负元组而被分类为正元组的数量;FN(False Negative)指实际为正元组而被分类为负元组的数量.本文中把“严重”类别当做正元组,因为该类拥有更大的错误代价.

综合考虑精度和召回率,可以使用F分数度量,其含义是精度和召回率的调和均值,计算公式为

为了比较各模型的有效性,另加入基准模型作为标准,一般认为只有准确率高于基准模型,该模型的建立才是有意义的.基准模型的准确率是指不使用任何指标进行预测所能达到的最大准确率,即数量占多数的类的比例.由于本文使用的数据几乎不存在类的不平衡问题,所以基准模型的准确率约为50%.此次实验的最终计算结果参见表4.

表4 各模型预测准确率Tab.4 Prediction accuracy for each data

3 结果分析

通过表4可以看出,在准确率方面,三个预测模型的准确率均高于基准模型的0.527 6,说明预测模型的建立是有意义的.其中随机森林的预测准确率最高,达到0.769 9,支持向量机次之,而神经网络的准确率最低,为0.729.对于样本的总体识别率,随机森林的表现最好.

精度方面,随机森林的预测精度最高,达到0.7886,高于支持向量机的0.754以及神经网络的0.7366.说明在对犯罪风险作出预测时,随机森林的预测结果相比于神经网络和支持向量机要更精确,其结果的含金量更高.

召回率方面,随机森林的预测召回率也是最高,达到0.7192,高于支持向量机的0.7131以及神经网络的0.6897.说明对于所有的有严重犯罪倾向的犯罪嫌疑人,随机森林作出的预测结果相比于神经网络和支持向量机覆盖率更高.

一般而言,预测的精度与召回率之间趋向于呈现逆关系,提高一个的代价往往是降低另外一个,然而,随机森林在两方面相较于其他模型都表现良好,体现在F分数上就是,随机森林的F分数取得0.752 3,高于神经网络的0.712 4以及支持向量机的0.733.

稳定性方面,随机森林0.018 4的总体准确率标准差也是最稳定的一个,预测结果的波动性最小,好于神经网络的0.022 4与支持向量机的0.020 8.

综合各方面结果可以得出,随机森林模型对于犯罪风险的预测更为出色.

4 结论

随机森林作为一种组合分类模型,克服了单个决策树分类时的局限性,同时对于数据的噪声有更强的鲁棒性,能够有效地避免过度拟合的问题,并且随着森林中树的棵数的增加,泛化误差趋于一个上界.实验结果表明,针对犯罪信息噪声多、属性复杂的特点,随机森林模型在风险预测中的应用相较于神经网络与支持向量机模型表现出更好的适应性与准确性.本文运用随机森林方法选择的预测指标,避免了以往预测模型中指标选择的主观性与盲目性,也证明了指标集的选择存在一个最优子集,并非以往观念中的指标越丰富越好.作为数据挖掘在犯罪领域的应用,本文提出的随机森林犯罪风险预测模型为实际的犯罪风险预测工作提供了一定的参考.

[1]赵军.我国犯罪预测及其研究的现状、问题与发展趋势[J].湖南大学学报(社会科学版),2011,25(3):155-160.

[2]金光,钱家麒,钱江波,等.基于数据挖掘决策树的犯罪风险预测模型[J].计算机工程,2003,29(9):183-185.

[3]王慧,王京.属性约简的决策树分类算法对未成年人犯罪行为的分析[J].中国人民公安大学学报(自然科学版),2011(4):29-32.

[4]李明,薛安荣,王富强,等.犯罪量动态优化组合预测方法[J].计算机工程,2011,37(17):274-278.

[5]于红志,刘凤鑫,邹开其.改进的模糊BP神经网络及在犯罪预测中的应用[J].辽宁工程技术大学学报(自然科学版),2012, 31(2):244-247.

[6]陈鹏,胡啸峰,陈建国.基于模糊信息粒化的支持向量机在犯罪时序预测中的应用[J].科学技术与工程,2015,15(35):54-57.

[7]HAN J W,MICHELINE K,PEI J.数据挖掘:概念与技术[M].北京:机械工业出版社,2015:245-249.

[8]BREIMAN L.Random forests[J].Machine Learning,2001,45(1):5-32.

[9]方匡南,吴见彬,朱建平,等.随机森林研究方法综述[J].统计与信息论坛,2011,26(3):32-38.

[10]林成德,彭国兰.随机森林在企业信用评估指标体系确定中的应用[J].厦门大学学报(自然科学版),2007,46(2):199-203.

[11]张华伟,王明文,甘丽新.基于随机森林的文本分类模型研究[J].山东大学学报(理学版),2006,41(3):139-143.

[12]ANANTHA M P,LOUIS R I,ANDY L.Newer classifi cation and regression tree techniques:Bagging and random forests for ecological Prediction[J].Ecosystems,2006,9:181-199.

[13]CAROLIN S,ANNE L B,THOMAS K,et al.Conditional variable importance for random forests[J].BMC Bioinformatics,2008,9:307-317.

[14]VERIKAS A,GELZINIS A,BACAUSKIENE M.Mining data with random forests:A survey and results of new tests[J].Pattern Recognition,2011,44:330-349.

[15]RAMON D U,SARA A.Gene selection and classifi cation of microarray data using random forest[J].BMC Bioinformatics,2006,7:3-15.

[16]姚登举,杨静,詹晓娟.基于随机森林的特征选择算法[J].吉林大学学报(工学版),2014,44(1):137-141.

[17]CAROLIN S,ANNE L B,ACHIN Z,et al.Bias in random forest variable importance measures:Illustrations, sources and a solution[J].BMC Bioinformatics,2007,8:25-45.

(责任编辑：李艺)

A forecasting model of crime risk based on random forest

WANG Yu-chen,GUO Zhong-yang,WANG Yuan-yuan
(School of Geographic Sciences,East China Normal University,Shanghai 200241,China)

Crime prediction has always been an outstanding issue for public security department.Random forest is a combined classification method with high accuracy,high speed,and stable performance,which is suitable for solving the problem of predicting crime risk.In the meantime,this method can choose the index group for predicting crime risk more objectively.As proved by studies,the index group chosen by random forest method can signifi cantly improve the accuracy of prediction,and the predictive model based of this method is more accurate and stable,so it can meet the demand of crime risk prediction.

random forest;crime risk prediction;index group selection

TP18

A

10.3969/j.issn.1000-5641.2017.04.008

1000-5641(2017)04-0089-08

2016-06-28

国家自然科学基金人才培养项目(J1310028)

王雨晨,男,硕士研究生,研究方向为数据挖掘.E-mail：wangyc ecnu@qq.com.

过仲阳,男,教授,博士生导师,研究方向为数据挖掘和遥感图像处理. E-mail：zyguo@geo.ecnu.edu.cn.