随机吸烟模型的持久性与灭绝性

张雪康,张振中

(东华大学数学系,上海201620)

随机吸烟模型的持久性与灭绝性

张雪康,张振中

(东华大学数学系,上海201620)

考虑随机因素的影响,提出了一个由布朗运动驱动的随机吸烟模型.首先,利用Lyapunov方法证明了随机吸烟模型具有全局正解性.其次,给出了该随机吸烟模型灭绝性和持久性的充分必要条件.最后运用伪极大似然方法估计出随机吸烟模型中的参数.

布朗运动;持久性;灭绝性

0 引言

吸烟距今已有数百年历史,不仅危害人体健康,而且还会对社会产生一定的不良影响.据世界卫生组织报告[1]显示:①有一半以上的吸烟者会死于与吸烟相关的疾病;②每年大约有600万人死于吸烟,其中大约有500万人死于直接吸烟,60万人死于二手烟.全球近10亿烟民,大约有80%的烟民是来自中低收入国家.香烟本身还具有大量的致癌物质或有毒物质,已知的至少有250种,对人体健康的危害极大.

虽然吸烟问题引起了人们的广泛关注,但是现有的研究论文中,吸烟理论研究文献比较少.1997年Garsow等人[2]首次使用微分方程来刻画潜在吸烟者、吸烟者与戒烟者.2008年, Sharomi和Gumel[3]在前者的基础上进一步考虑临时戒烟者,得到了局部和全局渐近稳定的充分条件.近来,Zaman[4]在Garsow等人[2]的基础上,考虑偶尔吸烟者的影响,并给出了全局渐近稳定的充分条件.最近,Alkhudhari等人[5]基于以下假设来刻画吸烟模型.

(1)非吸烟者x1(t)、吸烟者x2(t)、戒烟者x3(t)的单位死亡率分别为µ1、µ2、µ3.

(2)每单位新增人口为Λ.

(3)吸烟者x2(t)的戒烟率为γ.

(4)平均每个吸烟者使βx1(t)个非吸烟者成为吸烟者x2(t).

(5)平均每个吸烟者使αx3(t)个临时戒烟者成为吸烟者x2(t).

根据上述假设,可写出常微分方程

其中,x1(0)＞0,x2(0)＞0,x3(0)＞0.

虽然由常微分方程建立的确定性吸烟模型在一定程度上比较好地刻画了吸烟种群(潜在吸烟者、吸烟者、戒烟者、永久戒烟者)的动力学行为,但是注意到确定性的吸烟模型假定死亡率µi,i=1,2,3是确定的常数,在现实世界中,许多随机因素(地震、台风、车祸、其他意外因素)使得人口死亡率(包括吸烟种群)为随机变量.若随机因素相互独立且方差有限,则由著名中心极限定理知,一系列相互独立意外因素的累计会使得死亡率µi,i=1,2,3渐近服从正态分布,即

其中,Bi(t),i=1,2,3是标准布朗运动,σi表示干扰因素Bi(t)的强度.为了数学容易处理,假定B1(t),B2(t),B3(t)相互独立.

将式(2)代入式(1),可得

其中,x1(0)＞0,x2(0)＞0,x3(0)＞0,Λ＞0,0＜µ,β＜1,γ＜1,α＜1和σi＞0,i=1,2,3.随机微分方程(3)被称为随机吸烟模型.

从方程形式来看,随机吸烟模型式(3)似乎为一类特殊传染病方程.但是确定的吸烟模型与当前广泛研究的SI模型和SIR模型有本质的区别,具体如下.

(1)当x3(t)=0时,吸烟模型(1)即为SI传染病模型.

(2)吸烟模型(1)与SIR传染病模型有实质性区别.注意到SIR模型的康复者(Recovery)满足方程

其中,r表示感染者I(t)康复率,µ表示康复者R(t)的死亡率.

吸烟模型d x3(t)与SIR模型d R(t)相比多了一项非线性增长项αx2(t)x3(t),正是多了这个非线性增长项αx2(t)x3(t),使得在数学上处理吸烟模型不能直接平行推广SI模型与SIR模型的V函数等技巧.

有许多学者已经研究了随机噪声对人口种群的影响,如Gard[6]讨论了当随机噪声强度较弱时,随机模型依然保持持久性;Gray等人[7]讨论了当随机噪声较大时会导致被疾病感染者会以概率1灭绝;Bao和Yuan[8]给出了随机人口模型在L´evy噪声影响下具有一些渐近性质的充分条件;Lahrouz等人[9]考虑一个随机吸烟模型并给出了该随机模型渐近稳定的充分条件.

受到上述工作的启发,人们自然提出以下3个问题.

(1)在什么条件下,随机吸烟模型(3)具有全局正解性?

(2)在什么条件下,吸烟者x2(t)将随机一致有界以及随机持久?

(3)在什么条件下,吸烟者x2(t)将以概率1灭绝?

本文将回答以上3个问题.

1 全局正解

考虑F的部分σ-代数构成的域流{Ft}t≥0,如果当0≤s≤t＜∞时,有{Fs}⊂{Ft}⊂{F}且Ft=∩s＞tFs,那么{Ft}t≥0称为右连续域流。域流{Ft}t≥0满足的通常条件是右连续且F0包含所有的零测集.Bi(t),i=1,2,3是定义在这个概率空间(Ω,F,{Ft}t≥0,P)上相互独立的布朗运动.

本文假设(H):总人口数N(t)是个有界的确定函数,即,

其中,N(t)=P(t)+S(t)+Q(t),N和N1是正常数.

为方便处理,引进记号

定理1对∀x(0)=(x1(0),x2(0),x3(0))∈随机微分方程(3)存在一个唯一的全局正解x(t)=(x1(t),x2(t),x3(t))∈,并且该解以概率1位于中,即

其中inf∅=∞(∅表示空集).显然τm随着m→∞单调递增.令τ∞=τm,则τ∞≤τe几乎必然成立.若我们能够证明τ∞=∞几乎必然成立,则τe=∞几乎必然成立,进而可得方程(3)有唯一正解.

若式(4)不成立,则存在T＞0和ε∈(0,1)使得

即存在整数m1≥m0,使得当m≥m1时,有

首先,我们构造Lyapunov函数

对过程x(t)使用Itˆo公式,则对任意的0≤s≤τm∧t和m≥m1满足

其中,

即

其中,

又由不等式

可得

将式(8)代入式(7)可得

其中

将式(9)代入式(6),可得

由Gronwall不等式,可得

令Ωm={τm≤T},m≥m1.由式(5)得P(Ωm)≥则对∀ω∈Ωm,由停时的定义可知x1(τm,ω),x2(τm,ω),和x3(τm,ω)三者之一至少有一个等于或m,则

从而由式(10)和式(11)可得

其中IΩm是Ωm的示性函数.令m→∞有

所以必有τ∞=∞几乎必然成立.证毕.

2 随机吸烟模型的渐近性质

2.1 灭绝性

定理2若RS＜1,则对∀x2(0)∈R+,x2(t)都有

几乎必然成立.

证明由定理1,可知x2(t)以概率1位于R+中.运用Itˆo公式,可有

两边从0到t积分,可得

其中M1(t)=

M1(t)的二次变差为

由鞅的大数定理[11]可得

几乎必然成立.因此,由式(12)和式(13)可得

几乎必然成立.由L’Hospital法则可知,当RS＜1时,有x2(t)几乎必然指数趋近于0.证毕.

2.2 均值意义下随机弱持久

本节我们将讨论x2(t)在RS≥Rs＞1的情况.

定义1[12]若

几乎必然成立,则x2(t)(∀x2(0)∈R+)将在均值意义下随机弱持久.

定理3若RS≥Rs＞1和假设(H)成立,则x2(t)(∀x2(0)∈R+)将在均值意义下随机弱持久.

证明由定理1,可知x2(t)以概率1位于R+中.运用Itˆo公式,可有

两边从0到t积分,可得

可以看出M2(t)是一个局部鞅且二次变差

由指数鞅不等式[13],对任意的正常数T0,δ,和τ,知

其中,θ＞1,u＞1.由Borel-Cantalli引理[11]知,对几乎所有的ω∈Ω,都存在一个随机整数k0=k0(ω)使得当k≥k0(ω)时,有

成立.这意味着,对几乎所有的0≤t≤uk,都有

几乎必然成立.将式(15)代入式(14)中,可得

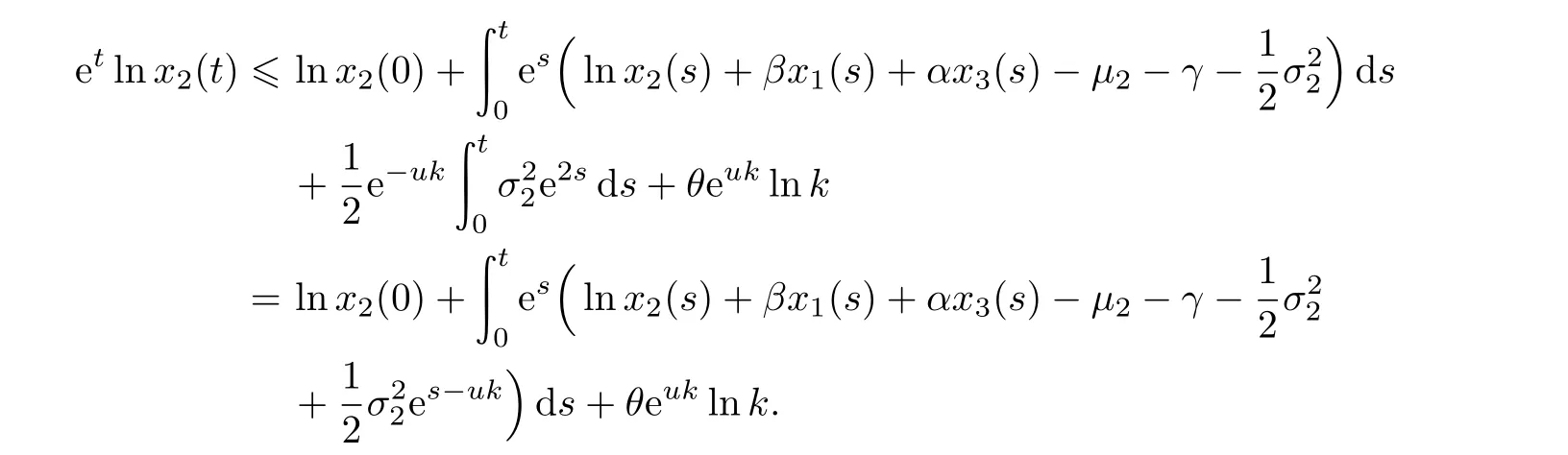
由假设(H)知,当∀0≤s≤uk和xi＞0,i=1,2,3时,存在一个与k独立的常数C,使得

成立.这也是说,对∀0≤t≤uk,恒有

成立.因此,当u(k−1)≤t≤uk和k≥k0(ω)成立时,我们有

令t→∞有

几乎必然成立.

下面我们证明

几乎必然成立.若不然,

由式(12)可得

因此,对

都有

几乎必然成立.将式(13)和式(14)代入式(17)中,得

显然这与式(16)矛盾.证毕.

我们可以看出当RS＜1时,吸烟者x2(t)将会以概率1趋近于0.当RS≥Rs＞1时,吸烟者x2(t)在均值意义下随机弱持久.那么当RS=1时,吸烟者x2(t)会是什么情况呢?接下来我们讨论RS=1时的情况.

定理4若RS=1,则对∀x2(0)∈R+,随机微分方程(3)的解x2(t)都有

几乎必然成立.

证明由定理1,可知x2(t)以概率1位于R+中.由式(13)知,对任意给定的ε＞0,几乎所有的ω∈Ω,都存在一个足够大的随机整数T1=T1(ω),使得当t≥T1(ω)时,有

几乎必然成立.又由RS=1知,当t≥T2≥T1(ω)时,有

将式(19)和式(20)代入式(12)中,可得,当t≥T2时,

对式(21)两边同时从T2到t积分,则有

由式(22)可得

这也就是说,我们已经证明了

由L’Hospital法则可得

几乎必然成立.又由于ε的任意性,所以

几乎必然成立.证毕.

2.3 随机持久

前一节,我们已经证明了若随机吸烟模型(3)的基本再生数RQ＞1,则吸烟者样本轨道随机弱持久.然而,对于实践与管理人员来说,若能给出吸烟者的数目介于两个正数之间,则更具有现实意义.而在生物模型中,将吸烟者介于两个正数之间,称之为随机持久.

定义2[14-15]若对∀ε∈(0,1),存在正常数M1=M1(ε)和M2=M2(ε)都有

成立,则x2(t)(∀x2(0)∈R+)随机持久.

定义3[15]若对∀ε∈(0,1),存在一个正常数H=H(ε),都有

成立,则x2(t)(∀x2(0)∈R+)随机一致有界.

从上述定义,我们可以看出随机持久意味着随机一致有界.首先,我们x2(t)的随机一致有界.

定理5若假设(H)满足,则

(i)对任意实数p≥1,存在一个仅仅依赖于p的常数K,都有

成立.

(ii)x2(t)随机一致有界.

证明(i)由定理1,可知x2(t)以概率1位于R+中.对(x2∈R+)使用Itˆo公式,可得

接下来,我们考虑方程

其中,x2(0)≤y(0).再次运用公式,可得

其中,

由假设(H),可知函数H(y,t)关于y一致有界,即存在一个常数K＞0,使得

成立.对式(23)两边同时积分并取期望以及式(24),可得

因此,有

又由比较定理[16],可得

因此

(ii)可由Chebyshev不等式得证.证毕.

接下来,我们讨论吸烟者x2(t)的随机持久.

定理6若假设(H)和RQ＞0成立,则x2(t)将随机持久.

首先,我们考虑方程

其中y(0)≤x2(0).然后,对U(y(t))使用公式,可得

令

再令

其中

由条件RQ＞0,t≥0以及假设(H)知,存在一个正常数ρ＞0,满足

由式(26)可得

令

则有

因此,存在一个常数K1＞0,使得

成立.对式(25)两边同时积分并取期望以及式(27),可得

由式(28),可知

由比较定理知

所以,

由Chebyshev不等式可知,对任意的ε＞0,有

因此,

即

又由定理5,可得x2(t)随机持久.证毕.

3 参数估计

在这一节中,我们讨论随机吸烟模型中参数Λ,µ1,µ2,µ3,β,γ,α,的估计.经过我们计算,直接使用伪极大似然方法可以得到含有参数的非线性似然方程,非线性方程无显示解.因此,我们先用x1(t),x2(t),x3(t)的轨道性质估计参数的近似值,随后运用伪极大似然方法估计出参数Λ,µ1,µ2,µ3,β,γ,α.本节所采用的二次变差方法估计扩散系数类似于Zhang等人[17]的研究.

两边从0到T积分,可得

ln x1(t)在区间[0,T]上的二次变差为

又由Klebaner[18]中的式(8.20)可得

以及

因此,可得

几乎必然成立,即

几乎必然成立.同理可得

几乎必然成立,以及

几乎必然成立.

又由二次变差定义知,对任意半鞅X(t),都有

其中∆t=max1≤κ≤n0=≤≤···≤=t.因此,当n→∞,∆t→0且T=n∆t时,有

接下来,我们将使用极大似然估计方法来估计出方程(29)的参数µ1,µ2,µ3,Λ,γ,β,α.考虑以等距时间点列0,∆t,2∆t,···,n∆t,可得方程(29)的离散系统

其中,εi,κ(i=1,2,3)是相互独立同分布(independent identically distributed,i.i.d),分布为均值为0、方差为1的标准正态分布的序列,并且对每一个κ,εκ= (ε1,κ,ε2,κ,ε3,κ)与{(xl,p,x2,p,x3,p), p＜κ}相互独立.此外,当ij(i,j=1,2,3)时,εi,κ与εj,κ也相互独立.

设(x1,0,x2,0,x3,0),(x1,1,x2,1,x3,1),···,(x1,n,x2,n,x3,n)是由过程(30)得到的观测序列,且Fκ−1=σ((x1,p,x2,p,x3,p),p≤κ−1).若给定Fκ−1,(x1,κ,x2,κ,x3,κ)的条件概率密度函数为

若给定F0,则(x1,0,x2,0,x3,0),(x1,1,x2,1,x3,1),···,(x1,n,x2,n,x3,n)的联合条件概率密度函数为

则可以得到条件对数似然函数为

式(31)的似然方程为

即

其中,

Dj,j=1,2,···,7是把行列式D的第j列的元素换以方程组的常数项b1,b2,···,b7而得到的7阶行列式.这就得到了参数Λ,µ1,µ2,µ3,β,γ,α的极大似然估计.

[参考文献]

[1]World Health Organization.Tobacco fact sheet[EB/OL].[2016-03-01].http://www.who.int/mediacentre/factsheets/fs339/en/.

[2]CASTILLO-GARSOW C,JORDAN-SALIVIA G,RODRIGUEZ-HERRERA A.Mathematical models for the dynamics of tobacco use,recovery and relapse[EB/OL].[2016-03-01].https://ecommons.cornell.edu/handle/ 1813/32095.

[3]SHAROMI O,GUMEL A.Curtailing smoking dyanamics:A mathematical modeling approach[J].Applied Mathematics and Computation,2008,195(2):475-499.

[4]ZAMAN G.Qualitative behavior of giving up smoking models[J].Bulletin of the Malaysian Mathematical Sciences Sciences Society,2011,34(2):403-415.

[5]ALKHUDHARI Z,SHEIKH S,TUWAIRQI S.Global dynamics of a mathematical model on smoking[J].ISRN Applied Mathematics,2014,Article ID 847075.

[6]GARD T C.Persistence in stochastic food web models[J].Bulletin of Mathematical Biology,1984,46(3):357-370.

[7]GRAY A,GREENHALGH D,HU L,et al.A stochastic diff erential equations SIS epidemic model[J].Siam Journal on Applied Mathematics,2011,71(3):876-902.

[8]BAO J,YUAN C.Stochastic population dynamics driven by L´evy noise[J].Journal of Mathematical Analysis and Applications,2012,391(2):363-375.

[9]LAHROUZ A,OMARI L,KIOUACH D,et al.Deterministic and stochastic stability of a mathematical model of smoking[J].Statistics and Probability Letters,2011,81(8):1276-1284.

[10]MAO X.Exponential Stability of Stochastic Diff erential Equations[M].New York:Marcel Dekker,1994.

[11]MAO X.Stochastic Diff erential Equations and Applications[M].Chichest:Horwood Publishing Limited,1999.

[12]LIU H,MA Z.The threshold of survival for system of two species in a polluted environment[J].Journal of Mathematical Biology,1991,30(1):49-61.

[13]MAO X,YUAN C.Stochastic Diff erential Equations with Markovian Switching[M].London:Imperial College Press,2006:74.

[14]JIANG D,SHI N,LI X.Global stability and stochastic permanence of a non-autonomous logistic equation with random perturbation[J].Journal of Mathematical Analysis and Applications,2008,340(1):588-597.

[15]LI X,GRAY A,JING D,et al.Suffi cient and necessary conditions of stochastic permanence and exctinction for stochastic logistic populations under regime switching[J].Journal of Mathematical Analysis and Applications, 2011,376(1):11-28.

[16]KARATZAS I,SHREVE S.Brownian Motion and Stochastic Calculus[M].Second edition.Berlin:Springer, 2007:293.

[17]ZHANG X,ZHANG Z,TONG J,et al.Ergodicity of stochastic smoking model and parameter estimation[J]. Advances in Diff erence Equations,2016,274:1-20.

[18]KLEBANER F C.Introduction to Stochastic Calculus with Applications[M].Second edition.London:Imperial College Press,2005:219.

(责任编辑：李艺)

Permanence and extinction of stochastic smoking model

ZHANG Xue-kang,ZHANG Zhen-zhong
(Department of Mathematics,Donghua University,Shanghai 201620,China)

To characterize the eff ects of stochastic noises on smokers,a stochastic smoking model driven by Brownian motion has been proposed.First,a unique global positive solution is proved according to Lyapunov function method.Then,some suffi cient and necessary conditions for permanence and extinction are presented.Finally,the parameters of stochastic smoking model are estimated by the pseudo-maximum likelihood estimation.

Brownian motion;extinction;permanence

O211.63

A

10.3969/j.issn.1000-5641.2017.04.007

1000-5641(2017)04-0071-18

2016-05-18

国家自然科学基金(11301068,11401093,11471071),东华大学非线性科学研究所基金

张雪康,男,硕士研究生,研究方向为随机分析及其应用.E-mail：xxkzhang@126.com.