带阻尼项的分数阶差分方程的振动性和渐近性

2017-08-07芦伟

华东师范大学学报（自然科学版） 2017年4期

关键词：宿州差分阻尼

芦伟

(宿州学院数学与统计学院,安徽宿州234000)

带阻尼项的分数阶差分方程的振动性和渐近性

芦伟

(宿州学院数学与统计学院,安徽宿州234000)

使用广义的Riccati技巧，研究了一类具有阻尼项的分数阶差分方程得到了其解的振动性的一些新准则.所得的结果改进和推广了某些分数阶离散方程的结果.

分数阶差分方程;阻尼项;振动性

0 引言

近年来,各类分数阶微分和差分方程的发展和应用方兴未艾,如在粘弹性理论、电子环路、控制理论、统计分析等领域的研究和应用日益深入,参见文献[1-6]及其相关参考文献.随着各类微分（差分）方程的振动理论研究被广泛关注[7-15],特别是对含阻尼项的微分、差分以及在时间模上的动力方程的振动性研究得到学者的重视[8,12-15],有些学者开始研究分数阶差分方程的振动性[15].受文献[8,13,15]的启发,我们研究了如下带阻尼项的分数阶差分方程这里,0＜α≤1且∆α表示α阶Riemann-Liouville算子,γ是奇正数之比.本文我们作如下假设.

(H1)r(t),p(t),q(t)都是正序列,且对充分大的t满足

(H2)f:R→R是连续函数；对一切的u(t)0和某个正数k,有u(t)f[u(t)]＞0且

1 准备知识

这部分我们将给出离散型分数阶微积分的基本知识.

定义1.1[1]令ν＞0,我们定义函数f的ν阶分数和分如下.

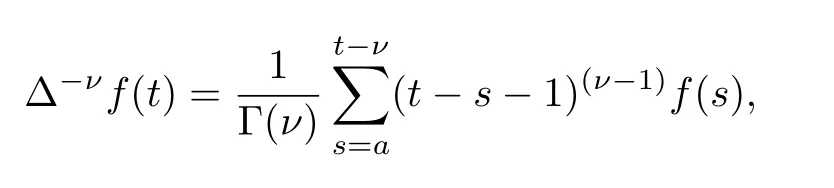
定义1.2[1]令µ＞0且m−1＜µ＜m,m是正整数,m=「µ」,置ν=m−µ，则f的µ阶分数差分定义如下.

引理1.3假设y(t)是方程(1)的一个解并且令

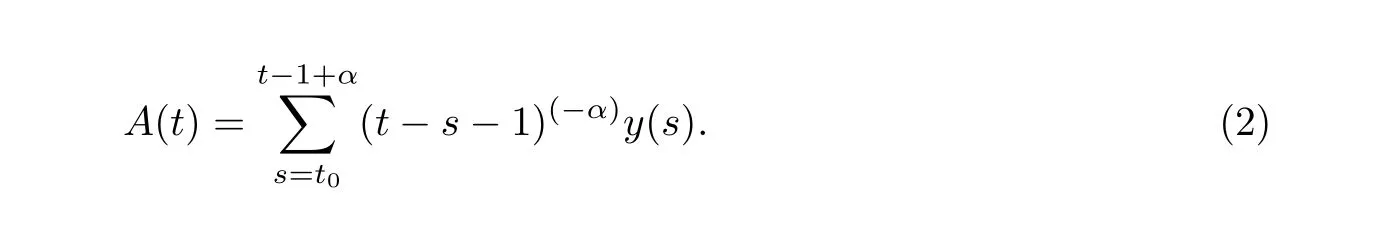
则有

证明

在后面的部分,我们将讨论如下两种情形.

2 主要结论及其证明

2.1(Ha)成立的情况

定理2.1假设(Ha)、(H1)、(H2)成立,y(t)是方程(1)的非振动解.则存在整数T≥t0,使得当t≥T时,有y(t)∆αy(t)＞0.

证明因为y(t)是方程(1)的非振动解,不失一般性,我们不妨假设对充分大的t,有y(t)＞0成立.由于(H2)的缘故可以类似证明y(t)＜0的情形,因此此种情况的证明省略.现在我们证明存在一个T≥t0,对于任意的t≥T,有∆αy(t)＞0.事实上,作相反假设,则存在t1≥T使得∆αy(t1)＜0或∆αy(t1)=0.

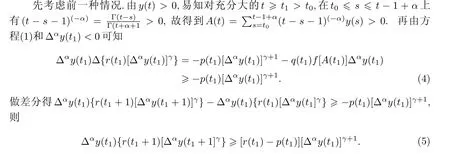
由(H1)知r(t1)−p(t1)＞0,因而式(5)右端大于零.故对于充分大的T,一定有∆αy(t1+1)＜0,再根据归纳法得到,当t≥t1时,∆αy(t)＜0.

对于后一种情况,由(H2)和方程(1)得∆{r(t1)[∆αy(t1)]γ}=−q(t1)f[A(t1)]≤0,这可推出∆αy(t1+1)≤0.若∆αy(t1+1)＜0,刚好可以用归纳法得到∆αy(t)＜0,t≥t1+ 1.若∆αy(t1+1)=0,重复上面的步骤,又可以推出∆αy(t1+2)≤0.反复用归纳法,总会有两种结果,即∆αy(t1+n)＜0,或∆αy(t1+n)=0.这是不可能的,因为q(t)是正序列,由方程(1)得0=∆{r(t1+n)[∆αy(t1+n]γ}+p(t1+n)[∆αy(t1+n)]γ=−q(t1+n)f[A(t1+n)]＜0,这是个矛盾.所以对充分大的t≥t1+1:=t2只会有∆αy(t)＜0.

对不等式(6)两边从t3到t−1求和,由(Ha)得

这与A(t)＞0相矛盾,故∆αy(t)＞0.证毕！

定理2.2假设条件(Ha)、(H1)、(H2)成立,进一步假设存在一个正序列b(s),满足

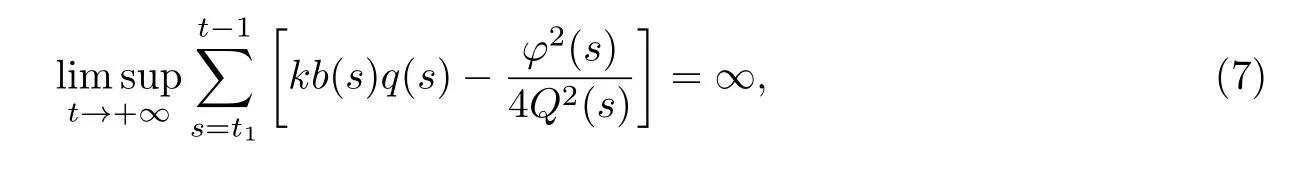
证明假设y(t)是方程(1)的非振动解,不失一般性,假设y(t)是方程(1)的最终正解,即y(t)＞0对充分大的t成立.由定理2.1,我们知道

定义黎卡提变换如下.

显然,在t≥T上v(t)≥0.直接计算得

健康雄性Wistar大鼠100只，体质量180～220g，由济南朋悦实验动物繁殖有限公司提供，实验动物生产许可证号SCXK（鲁）2016‐0007 。

由(8)式容易推出r(t)[∆αy(t)]γ≥r(t+1)[∆αy(t+1)]γ,又使用不等式xβ−yβ≥(x−y)β和(H2),有

对不等式(11)从t1到t−1求和,则当t≥t1时有

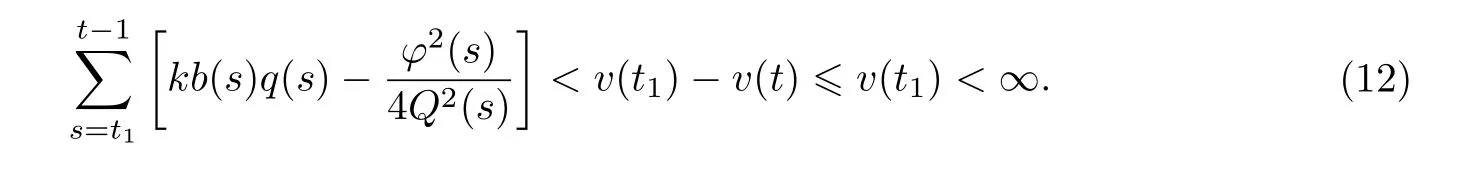
2.2 (Hb)成立的情况

这里我们需要如下条件.

(H3)假设t≥0,γ≥1,有∆f(t)≤0,且满足

定理2.3假设条件(H1)、(H2)成立,y(t)是方程(1)的非振动解,则∆αy(t)是最终定号的.

事实上,令y(t)是方程(1)的非振动解.不失一般性,我们假设当t≥t0时y(t)＞0.再假设对一切的t≥t0有∆αy(t)＞0,则我们的结论是成立的;反之,若存在某个t1≥t0有∆αy(t1)＜0或∆αy(t1)=0,则类似定理2.1的证明思路可得∆αy(t1)最终为负的.

定理2.4假设条件(H1)、(H2)、(H3)和(Hb)成立,进一步假设存在一个正序列b(t)使(7)式成立,其中φ(t),Q(t)与定理2.2中有相同的定义.则方程(1)的每个解都是振动的或趋于零.

假如∆αy(t)是最终正的,则显然可推出(8)成立.沿袭定理2.2的证明思路可以得到一个矛盾.

假如∆αy(t)是最终负的,则由(3)式知∆αA(t)是最终负的,limt→∞A(t)=l≥0.可以断定l=0,否则的话有A(t)≥l＞0.又因为f(u)是非减的,所以存在t2≥t1,满足f[A(l)]＞f(l).因此,由方程(1)我们得到

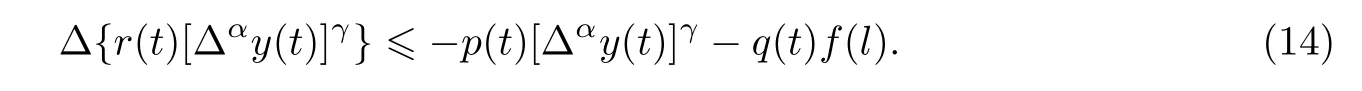
当t≥t2时,我们定义w(t)=r(t)[∆αy(t)]γ,则可以得出

使用不等式γxγ−1(x−y)≥xγ−yγ≥γyγ−1(x−y)(这里所有的x均不恒等于y且γ≥1),这就得到

对上边的不等式两边从t2到t−1求和得

根据(H3),我们使用分部作和的方法得

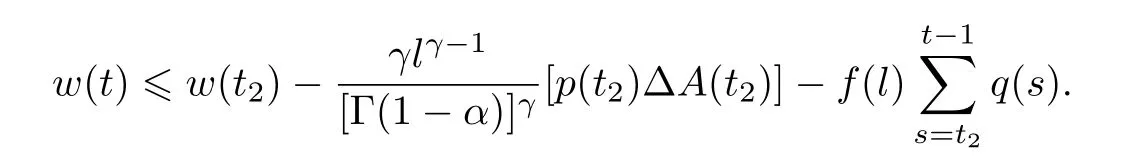
因此,当t≥t2时,有

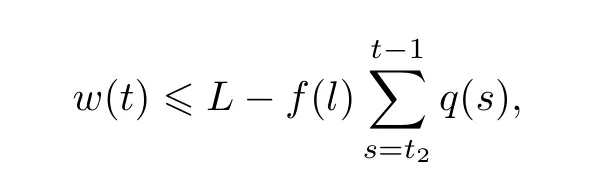
这推出

对上面的不等式两边从t3到t求和,推出

由条件(13)可以推出A(t)最终为负,这与A(t)≥l＞0矛盾.因此,定理的结论成立.

3 例子

例1考虑如下分数阶差分方程

所以,(Ha)成立.

因此,定理2.2的条件全部满足,故方程(18)是振动的.

例2再考虑分数阶差分方程

利用比值判别法可得

因而条件(Hb)成立.类似例1,容易验证条件(H1)、(H2)、(H3)成立.再取b(s)=s,有

故定理2.4的条件全部满足,所以方程(19)是振动的.

注1定理2.2中若选择不同的正序列b(s)会得到不同的结果,如选b(s)=sλ(λ＞ 1)或者b(s)=等可以得出相应的推论.

注2分数阶差分方程的Philos型振动性等问题可用同样的方法研究.

致谢本文中审稿专家给出了十分重要而中肯的意见,对此作者向审稿专家致以衷心的感谢！

[1]ATICI F M,ELOE P W.Initial value problems in discrete fractional calculus[J].Proc Amer Math Soc,2009, 137:981-989.

[2]GRACE S R,AGARWAL R P,WONG P J Y,et al.On the oscillation of fractional diff erential equations[J]. Fract Calc Appl Anal,2012,15:222-231.

[3]CHEN D X.Oscillation criteria of fractional diff erential equations[J].Advances in Diff erence Equations,2012, 33:1-10.

[4]PODLUBNY I.Fractional diff erential equations[M].San Diego:Academic Press,1999.

[5]HAN Z,ZHAO Y,SUN Y,et al.Oscillation for a class of fractional diff erential equation[J].Discrete Dyn Nat Soc,2013,2013:1-6.

[6]程金发,分数阶差分方程理论[M].厦门:厦门大学出版社,2010.

[7]LU W,GE W,ZHAO Z.Oscillatory criteria for third-order nonlinear diff erence equation with impulses[J]. Journal of Computational and Applied Mathematics 2010,234(12):3366-3372.

[8]芦伟,葛渭高.时标上二阶脉冲阻尼动力方程解的振动性和渐近性[J].生物数学学报,2013,28(2)：343-349.

[9]时宝,张德存,盖久明．微分方程理论及其应用[M].北京:国防工业出版社,2005.

[10]杨甲山,黄劲.时间模上一类二阶非线性动态方程振荡性的新准则[J].华东师范大学学报(自然科学版),2015(3):9-15.

[11]张晓建,杨甲山.时标上三阶时滞动力方程的振动性和渐近性[J].华东师范大学学报(自然科学版),2014(3):51-59.

[12]马晴霞,刘安平.Oscillation criteria of nonlinear fractional diff erential equations with damping term[J].应用数学, 2016,29(2):291-297.

[13]孙一冰,韩振来,孙书荣,等.时间尺度上一类二阶具阻尼项的半线性中立型时滞动力方程的振动性[J].应用数学学报,2013, 36(3):480-494.

[14]ZHENG B.Oscillation for a class of nonlinear fractional diff erential equations with damping term[J].J Adv Math Stud,2013,6:107-115.

[15]LI W N.Oscillation results for certain forced fractional diff erence equations with damping term[J].Advances in Diff erence Equations,2016,70:1-9.

(责任编辑：林磊)

Oscillation and asymptotics for damped fractional diff erence equations

LU Wei
(School of Mathematics and Statistics,Suzhou University,Suzhou Anhui 234000,China)