一类特殊混合跳-扩散模型的欧式回望期权定价

杨朝强

(兰州财经大学图书馆经典资料室,兰州730101)

征稿启事

一类特殊混合跳-扩散模型的欧式回望期权定价

杨朝强

(兰州财经大学图书馆经典资料室,兰州730101)

利用分数Girsanov公式和分数Wick-Itˆo-Skorohod积分,建立了一个基于标准布朗运动、分数布朗运动、Poisson过程的线性组合的金融市场模型,结合Merton假设条件以及风险资产所满足的随机微分方程的Cauchy初值问题,给出了混合跳-扩散模型下的欧式看跌期权定价的Merton公式,给出了混合跳-扩散分数布朗运动下连续支付红利的欧式固定履约价和浮动履约价的看涨回望期权及看跌回望期权定价公式.数值模拟与仿真结果验证了模型的有效性和准确性.

混合跳扩散分数布朗运动;Merton假设条件;分数Wick-Itˆo-Skorohod积分;欧式回望期权

0 引言

近年来关于抛物型随机偏微分方程模型的研究越来越受到学者们的关注,抛物型随机偏微分方程理论已经被广泛应用于随机过程与随机分析、金融数学与金融工程、运筹学与控制论等领域.混合分数布朗运动(mfBm)模型是一类特殊的抛物型随机微分方程,是高斯过程的衍生过程.众所周知的期权定价理论是金融数学和金融工程的核心理论,混合分数布朗运动是布朗运动和分数布朗运动的线性组合,已经被广泛地应用于期权定价理论.文献[1]最早把布朗运动和分数布朗运动组合在一起研究了欧式期权的定价；文献[2]研究了混合分数布朗运动样本轨道的Holder连续性和自相似性;文献[3-6]已经多次应用跳-扩散模型来刻画股票价格的随机跳行为,并给出了相应的期权定价公式,但这种跳-扩散模型无法处理Wick积分,同时无法定义适合的随机积分来刻画股价的变化,于是使用混合分数布朗运动来刻画金融资产的波动过程是比较合理的[7-10].由于分数布朗运动的Itˆo公式和分数Wick-Itˆo-Skorohod积分所建立的Black-Scholes(简称B-S模型)已经远远超越了B-S模型的定义和属性,学者们发现所建立的分数B-S模型不能准确地描述资产的浮动收益和金融市场的波动情形[9].事实上,由于分数布朗运动的自相似性、厚尾性和长程关联性,使得分数布朗运动既不是Markov过程又不是半鞅,这给随机分析和随机计算带来了极大的困难.于是有些学者[11-12]提出用混合跳-扩散分数布朗运动(mj-dfBm)模型来刻画金融市场的波动行为.

本文研究一类特殊的混合跳-扩散分数布朗运动模型,不同于文献[12]的混合跳-扩散分数布朗运动模型,本文的模型是基于标准布朗运动、分数布朗运动、Poisson过程的线性组合,利用Itˆo公式和分数Wick-Itˆo-Skorohod积分建立了一个新的市场定价模型,给出了连续支付红利的欧式固定履约和浮动履约回望期权的定价公式,为了刻画利率的异常波动情形.最后给出的数值模拟与仿真验证了模型的有效性.结果表明,本文的混合跳-扩散分数布朗运动模型便于计算,可操作性强,不但能有效地刻画金融市场的隐含波动率的变化,而且能够合理地解释金融市场的“微笑”现象.

1 预备及引理

定义1[1]设0＜H＜1,Hurst参数为H的分数布朗运动,是一个连续高斯过程定义含有参数α,β和H的混合分数布朗运动,是由Hurst参数为H的分数布朗运动和标准布朗运动的线性组合,定义概率空间(Ω,F,P),对任意的t∈R+,满足

其中Bt是标准布朗运动,是含有参数H的独立分数布朗运动,α,β是两个给定的实数且满足(α,β)(0,0).

性质1[2]混合分数布朗运动具有如下性质.

其中∧表示两个数中取最小;

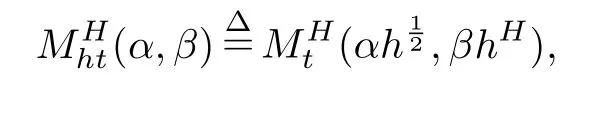
其中r是常数无风险利率.

引理1—引理5的证明详见文献[1,9,10].

2 混合跳扩散分数布朗运动定价模型与分数Wick-Itˆo-Skorohod积分

2.1 混合跳扩散分数布朗运动定价模型

假设某一支期权的价值Vt=V(St,t)依赖于St和t,动态股票价格满足如下随机微分方程

其中µ是期望收益率,σ1,σ2,Bt,的定义见引理3,Bt和是相互独立的.

引理6[11]设Vt=V(S,t)是二元可微函数.若随机过程St适合随机微分方程

引理7设Vt=V(St,t),V是二元可微函数.若随机过程St适合随机微分方程

证明假设d Pt服从如下形式的两点分布:

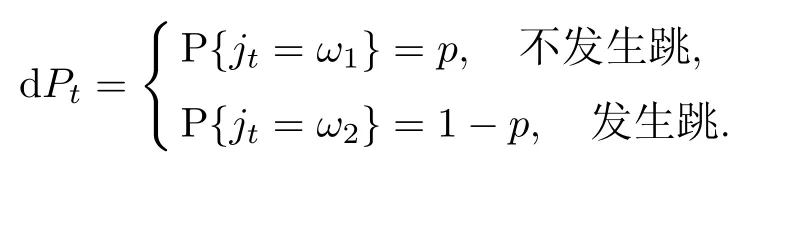
在时间区间[t,t+d t]内,可以确定事件ω1发生的概率为P(ω1)=1−λd t,事件ω2发生的概率为P(ω2)=λd t,记St+＞St表示股票价格St在t时刻上跳,St+＜St表示股票价格St在t时刻下跳,注意到非负,于是St+=St(1+jt)＞0.设∏是通过简单的对冲原理∇得到一个金融衍生产品,选取适当的∇使得投资组合在(t,t+d t)上是无风险的,即∏∏根据模型(3),投资组合∏有如下两种情况.

(i)如果跳事件不发生,对于二元可微函数Vt=V(S,t),利用公式,有

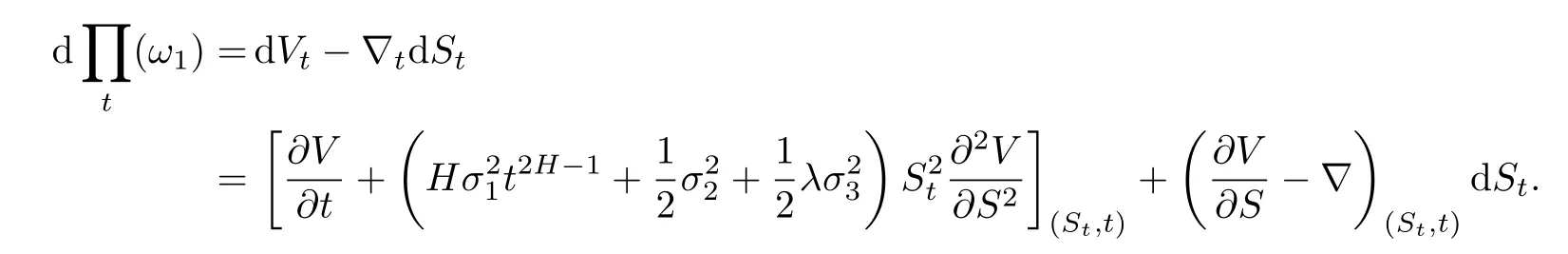
(ii)如果跳事件发生,则

于是在混合跳-扩散分数布朗运动模型中,欧式期权定价模型可以表示为含有期望算子的抛物型积分方程.

仿照引理6的证明,对二元可微函数d Vt泰勒展开,则有

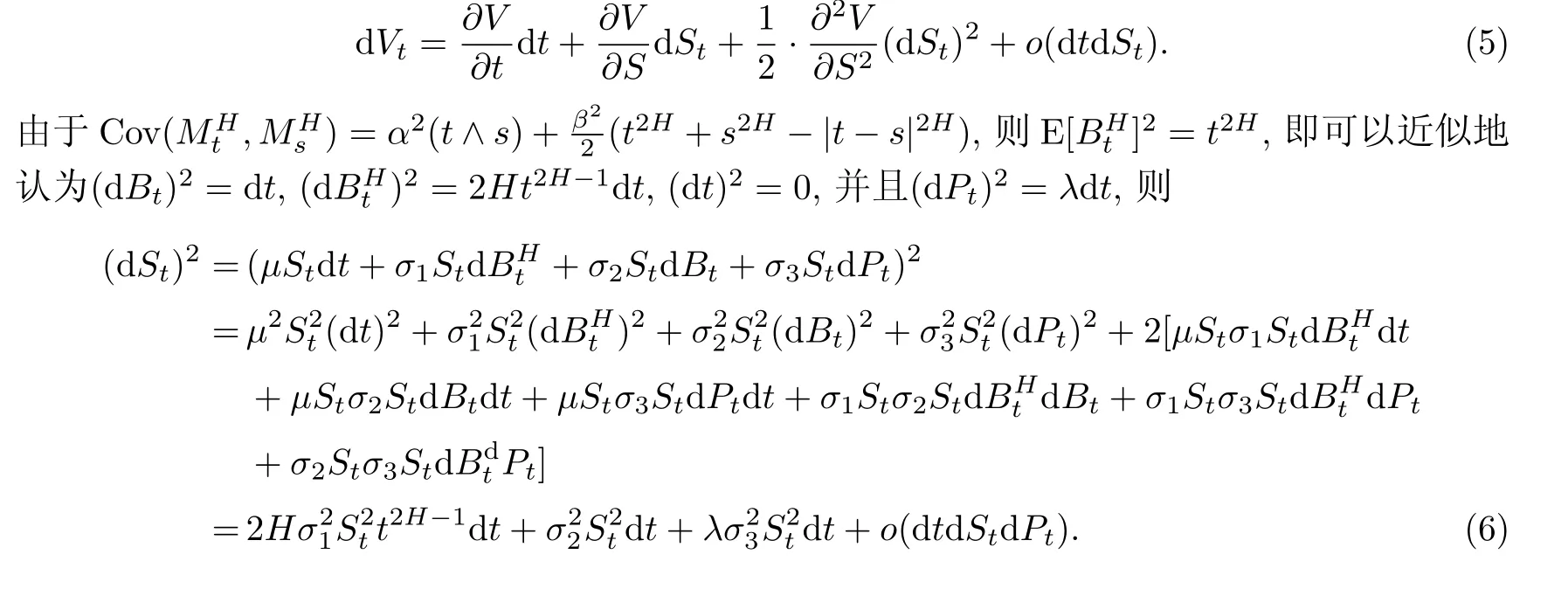
把式(6)代入式(5),可得

证毕.

2.2 分数Wick-Itˆo-Skorohod积分与混合跳-扩散分数随机微分方程

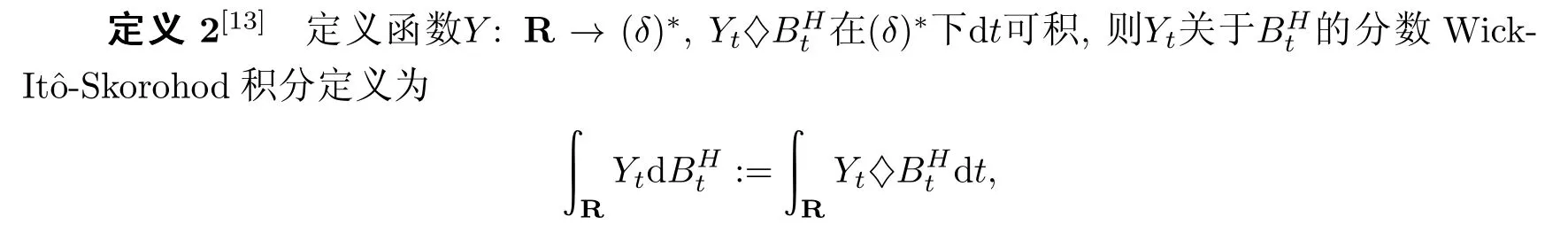
其中♢表示Wick乘积.

其中F,G∈(δ)∗H.

假设无风险利率的债券价格Bt满足

根据定义2,引理8和引理9,可以考虑如下混合跳-扩散分数随机微分方程

其中r是期望收益率,q是股息分红率,σ1,σ2,σ3都是常数,且Bt,BHt,Pt是相互独立的.作为原生资产的股票是连续支付股息红利的.

其中S≤Jn,E是V的期望算子.

3 主要结果

3.1 欧式固定履约回望期权和欧式浮动履约回望期权

回望期权是指该期权持有者在期权到期日可以观察期权有效期内标的资产价格的变化过程,通过选择资产价格的最高价格或最低价格进行交易,是一种典型复杂的新型奇异期权.设T为回望周期[T0,T]的终止时间,风险资产的价格St在t(0≤t≤T)时刻取得的最大值和最小值分别表示为[14]

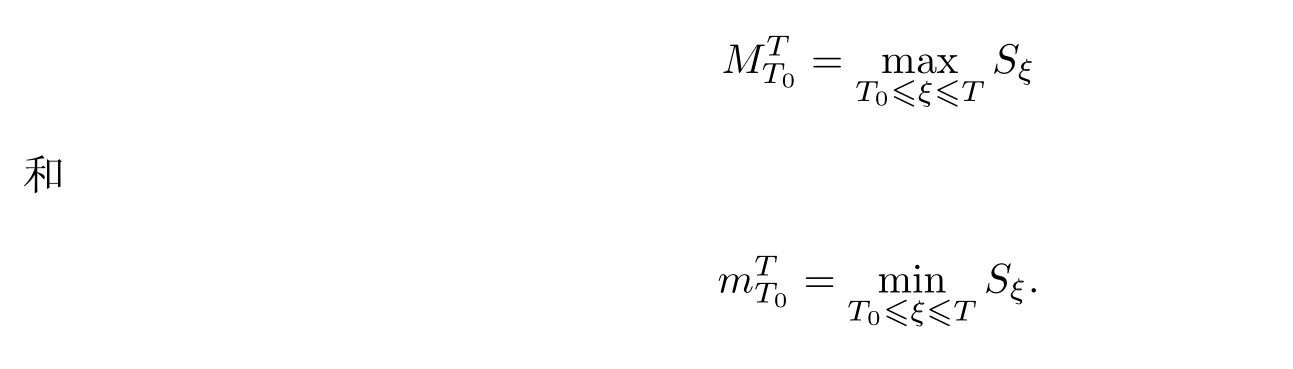
回望期权有固定履约回望期权和浮动履约回望期权两类.浮动履约回望看涨期权是指该期权持有者在回望期内有权利以最低的交易价格买入资产,浮动履约回望看跌期权是指该期权持有者在回望期内有权利以最高的交易价格买出资产,因此或者到期实际支付额看涨或看跌分别为.而对于固定履约回望期权是提前约定敲定价格K,固定履约看涨或看跌实际支付额分别为

引理10[14]假设一支欧式固定履约回望看涨期权的到期实际支付额为−K,设St=S,=M,Q为风险中性测度,则在任意t(T0≤t≤T)时刻回望看涨期权价格可表示为

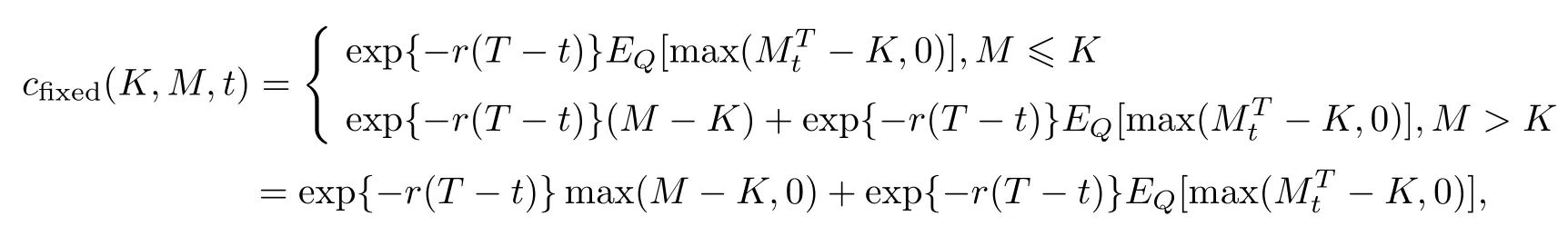
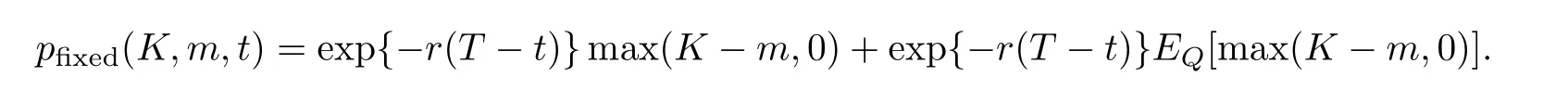
引理11[14]假设一支欧式浮动履约回望看涨期权的到期实际支付额为ST−设St=S,=m,,Q为风险中性测度,则在任意t(T0≤t≤T)时刻回望看涨期权价格可表示为

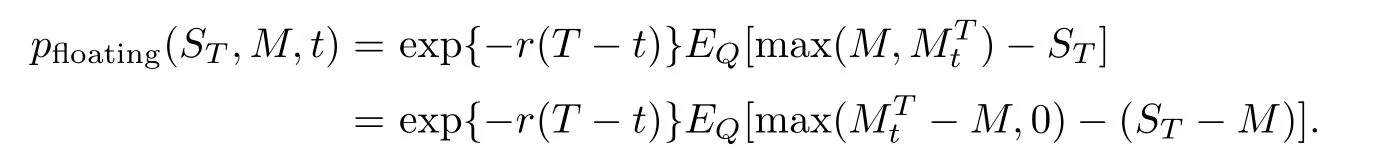
3.2 定价公式

设V(t,S,J)表示回望期权在任意t(T0≤t≤T)时刻的价格,根据2.2小节的讨论,欧式回望期权满足如下抛物型随机偏微分方程

其中T0≤t≤T,并且V(t,S,J)在如下区域连续可微. {

终端条件为

类似于引理10和引理11的推导,在(13)–(16)的条件下,下面以定理的形式给出欧式固定履约回望期权和浮动履约回望期权的定价公式.

定理1设到期日为T,对于欧式固定履约回望期权,在模型(13)的环境下欧式固定履约回望看跌和看涨期权的价格为

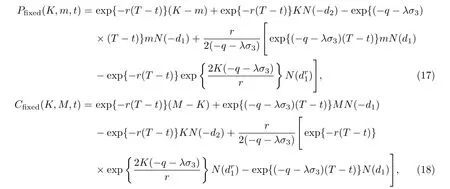
其中

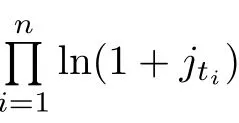
证明在风险中性金融市场,根据引理5和引理10,到期日为T的欧式固定履约回望看跌期权可以表达为

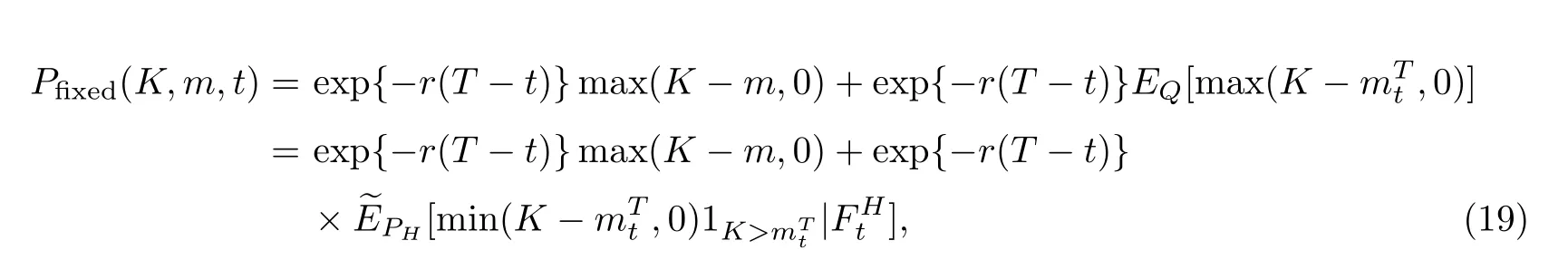
设

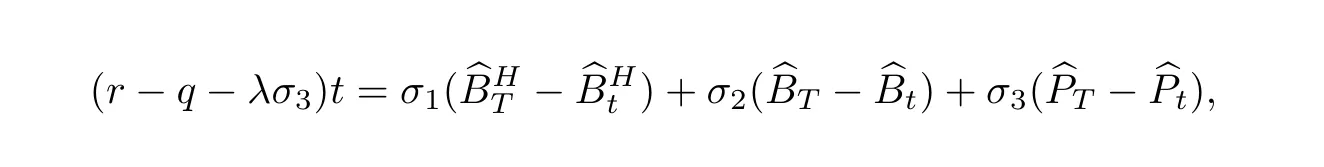
则

注意到Poisson跳过程的跳跃强度为λ,利用Poisson分布函数性质,得

利用同样的证明过程可以得到式(18).

对照引理11以及定理1,可以给出欧式浮动履约回望看跌和看涨期权的价格公式.

定理2设到期日为T,对于欧式浮动履约回望期权,在模型(13)的环境下欧式浮动履约回望看涨和看跌期权的价格为

证明过程类似于定理1.

注记1根据定理1和定理2,欧式固定履约回望看涨期权和看跌期权之间满足如下的平价关系

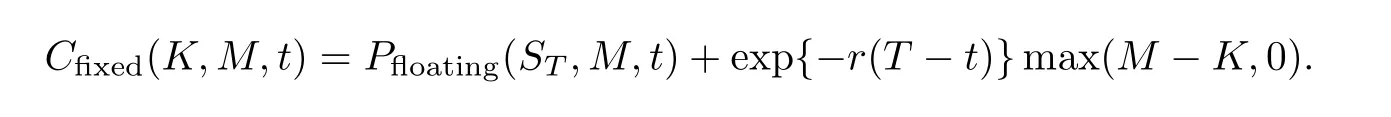
Eberlein E和Papapantoleon A[16]也得到了风险资产在L´evy跳过程的环境下欧式固定履约回望看涨期权和欧式浮动履约回望看跌期权之间的平价关系公式.

4 数值模拟及分析

4.1 几种定价模型的对比

对不含有跳过程的纯混合分数布朗运动(pmfBm)模型,含有跳过程的混合分数布朗运动(jmfBm)模型[7],以及本文的混合跳-扩散分数布朗运动(mj-dfBm)模型分别作一般假设下的理论价格对比,为了更突出模型之间的异同,参数的选择没有选取已有的实证数据,所有模拟结果由Matlab运行生成,模型所用到的所有参数值见表1.

表1 不同模型下选择的参数值Tab.1 The valuations of the chosen parameters used in these models

把表1的相应参数分别代入到各类模型中,记Pp−m,Pj−m,Pm−j分别为pmfBm模型, jmfBm模型,mj-dfBm模型下欧式固定履约回望看跌期权价格,计算结果见表2.

表2 不同模型下欧式固定履约回望看跌期权价格Tab.2 European lookback fi xed strike put option prices for various models

4.2 相关参数对模型的影响

考虑混合跳-扩散分数布朗运动下欧式固定履约回望看跌期权定价模型各参数的变化,在取不同的跳参数值时,相应的H,λ,µj,σj参数值的变化情况如图1所示.这里边界参数设定为r=0.025 0,q=0.032 0,σ1=0.107 3,K=100,H=0.558,J=0.003 5,t=0,T=2,λ= 7.68,µj=−000 721,σj=0.001 9,σ2=0.021 5,σ3=0.000 720 2.图1表明,回望看跌期权价格随着参数H,λ,µj,σj的单调增加而单调减少.类似的单调现象也出现在文献[12,15]中.

继续考虑混合跳扩散分数布朗运动下欧式固定履约回望看跌期权定价模型的隐含波动率变化,在选定参数r=0.025 0,q=0.032 0,σ1=0.107 3,K=100,H=0.558,J=0.003 5, t=0,T=0.5(年),λ=10.22,µj=−000 721,σj=0.001 9,σ2=0.021 5,σ3=0.000 720 2时,绘制曲面图形如图2所示.很显然,随着持有货币比率(m/K)的减少,在回望期权的有效回望期内,模型对回望期权的隐含波动率表现出明显的“微笑”现象.

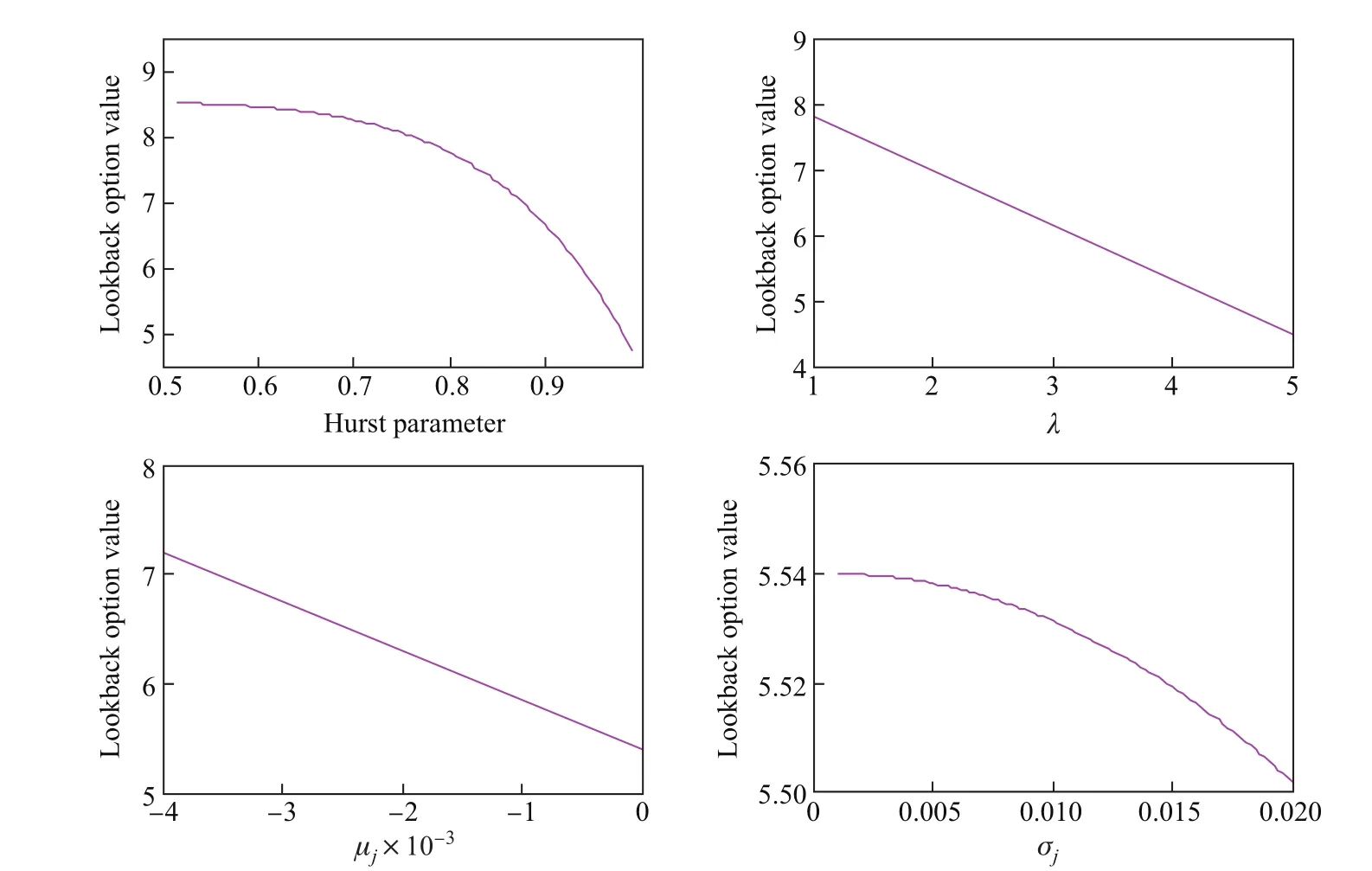
图1 不同参数下欧式固定履约回望看跌期权价格Fig.1 European lookback fixed strike put option prices for various parameters

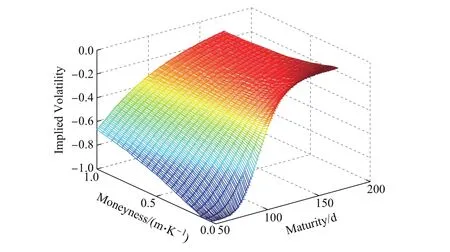
图2 混合跳-扩散分数布朗运动下欧式固定履约回望看跌期权模型的隐含波动率模拟Fig.2 Smile surface generated by the mj-dfBm model

5 结论

本文的定价模型考虑了标准布朗运动、分数布朗运动、Poisson过程的线性组合,利用Itˆo公式和分数Wick-Itˆo-Skorohod积分建立了一个新的市场定价模型,给出了连续支付红利的欧式固定履约和浮动履约回望期权的定价公式,通过具体数值和相关参数对定价公式的模拟验证,表明该模型在刻画期权在短期交割或长期交割前表现出的异常波动跳现象是相当合理的并且是有效性的,从回望看跌期权价格的递减表现上来看,明显略快于其他模型,更加接近不确定金融市场.本文的混合跳-扩散分数布朗运动模型便于计算,可操作性强,不但能有效地刻画金融市场的隐含波动率的变化,而且能够合理地解释金融市场的“微笑”现象.本文的结论在合理解释金融现象的同时,也丰富了期权定价理论,对其他类型奇异期权的研究以及一些复杂金融衍生品定价的研究具有参考意义.

[1]CHERIDITO P.Mixed fractional Brownian motion[J].Bernoulli,2001,7(6):913-934.

[2]MOUNIR Z L.On the mixed fractional Brownian motion[J].Journal of Applied Mathematics and Stochastic Analysis.2006,1-9.

[3]姜礼尚,罗俊.跳扩散模型下永久美式看跌期权定价[J].系统工程理论与实践,2008,28(2):10-18.

[4]CHANG M A,CHINHYUNG C,KEENWAN P.The price of foreign currency options under jump-diff usion processes[J].Journal of Futures Markets,2007,27(7):669-695.

[5]陈超.标的资产价格服从跳-扩散过程的脆弱期权定价模型[J].工程数学学报,2008,25(6):1129-1132.

[6]彭斌,彭菲.基于跳-分形模型的美式看涨期权定价[J].数学的实践与认识,2014,44(24):1-9.

[7]徐峰,郑石秋.混合分数布朗运动驱动的幂期权定价模型[J].经济数学,2010,27(2):8-12.

[8]孙玉东,师义民.混合分数布朗运动下亚式期权定价[J].经济数学,2011,28(1):49-51.

[9]XIAO W L,ZHANG W G.Pricing model for equity warrants in a mixed fractional Brownian environment and its algorithm[J].Physica A,2012,391(24):6418-6431.

[10]SUN L.Pricing currency options in the mixed fractional Brownian motion[J].Physica A,2013,392(16):3441-3458.

[11]杨朝强.一类混合跳-扩散分数布朗运动的欧式回望期权定价[J].山东大学学报(理学版),2013,48(6):67-74.

[12]FOAD S,ADEM K.Pricing currency option in a mixed fractional Brownian motion with jumps environment[J]. Mathematical Problems in Engineering.2014,2014(1):1-13.

[13]BIAGINI F,HU Y Z.Stochastic Calculus for Fractional Brownian Motion and Applications[M].London: Springer-Verlag,2008.

[14]YUE K K.Mathematical Models of Financial Derivatives[M].2nd ed.Berlin:Springer,2008:201-211.

[15]XIAO W L,ZHANG W G.Pricing currency options in a fractional Brownian motion with jumps[J].Economic Modelling,2010,27(5):935-942.

[16]EBERLEIN E,PAPAPANTOLENO A.Equivalence of fl oating and fi xed strike Asian and lookback options[J]. Stochastic Processes and Their Applications.2005,115(1):31-40.

(责任编辑：林磊)

Pricing European lookback option by a special kind of mixed jump-diff usion model

YANG Zhao-qiang
(Classic Library Reference Room,Lanzhou University of Finance and Economics, Lanzhou 730101,China)

By using fractional Girsanov formula and fractional Wick-Itˆo-Skorohod integral,based on a linear combination of Brownian motion,fractional Brownian motion and Poisson process,a new market pricing model is built.Under the conditions of Merton assumptions,we analyze the Cauchy initial problem of stochastic parabolic partial diff erential equations.Then the pricing Merton-formula of European option meets the pricing model for the European fixed strike and floating strike price of the lookback option. Finally the pricing formulas of fixed strike and floating strike lookback call option and lookback put option are proved.Numerical simulations illustrate that our model are valid and accurate.

mixed jump-diff usion fractional Brownian motion;Merton assumptions; fractional Wick-Itˆo-Skorohod integral;European lookback option

F830.91;O211.6

：A

10.3969/j.issn.1000-5641.2017.04.001

1000-5641(2017)04-0001-17

2016-09-02

兰州财经大学青年教师科研项目(Lzufe2017)

杨朝强,男,硕士,研究方向为随机过程与金融数学.E-mail：woyuyanjiang@163.com.