让思维“活水”在问题教学中升华

江苏省盱眙县铁佛初级中学 孟先瑞

让思维“活水”在问题教学中升华

江苏省盱眙县铁佛初级中学 孟先瑞

在数学教学中，教师经常需要应用问题教学引导学生学习，如何应用问题教学培养学生的思维水平是每一名数学教师都很关注的问题。教师在教学中可以应用提出经典问题培养学生的学习兴趣、应用阶梯式持续提问法逐步提高学生的思维水平、应用鼓励学生拓展问题的方法激发学生的发散思维能力。教师应用这样的提问教学法，可以让学生主动地思考问题，学生在思考的过程中思维水平能逐渐提高。

初中数学；数学教学；问题教学

问题教学，是指教师应用提出问题的方法为学生创造学习情境，让学生通过思考、解答问题来思考、掌握知识，提高数学水平的教学方法。

一、应用问题教学引导学生思考

教师在开展教学活动的时候，如果直接向学生灌输知识，那么学生学习知识的过程将是枯燥的，从而不愿意积极地学习知识。教师要意识到，如果教师“要”学生学习，那么学生的学习效率往往比较低下，假如教师抛出一个有趣的数学问题，学生就会为了解决这个问题去思考，学生在思考的过程中，教师就能引导学生理解要如何解决问题。

以一名教师引导学生理解如何列一元一次方程为例，教师可以引导学生看清朝数学家徐子云的诗：“三百六十四只碗，看看用尽不差争，三人共食一只碗，四人共吃一碗羹，请问先生明算者，算来寺内几多僧？”很多学生觉得这样的诗像顺口溜一样很好玩，抛出的数学问题又很有趣，于是愿意学习这个问题。教师引导学生思考，在这道题中，给出的已知条件是什么？要求的答案是什么？学生经过思考，得到以下的已知条件：（1）共有364只碗，并且碗全部用光；（2）三个和尚共用一个大饭碗；（3）四个和尚共用一个大汤碗。需要求的答案是寺内共有几个和尚。教师引导学生思考：现在要以哪个相等的量列方程呢？学生表示，在这个数学问题中最明晰的数量是碗的数量364，应以碗的数量作为等量。教师引导学生思考：那么如何设元，并给出关系式，才能让方程两边相等呢？学生经过思考，认为可以设和尚的人数为未知元。其中一个和尚用了1/3个饭碗及1/4个汤碗，那么一个和尚用的碗就是1/3+1/4个碗，列方程为（1/3+1/4）x=364。解得x=624。学生通过解答这道题，理解了列方程式的要领：第一，找出一个最明晰的数字，作为等量标准；第二，结合等量标准给出等量关系式；第三，如果等量关系式不能直接得到，可以应用转换的方法得到等量关系式。

教师在开展教学活动的时候，要给出有趣的问题引导学生思考，让学生在思考中获得知识，在体验的过程中获得学习的成就感。只要教师持续用这种方法开展教学活动，就能让学生愿意思考、愿意学习。

二、应用连续问题引导学生探索

教师在开展教学的时候，有时会遇到一个问题：教师提出的问题太困难，很多学生回答不出来，于是产生消极的学习心理，不愿意再探索知识。教师要意识到，学生的层次有差异性，如果直接给学生提出过于复杂、过于抽象的问题，学生可能会感受到学习的挫折感，教师可以应用阶梯式连续提问法帮助学生打好学习基础，引导学生探索问题。

以教师引导学生学会计算图形的面积为例，如果教师直接引导学生思考计算图2的数学问题：两个正方形的边长都为1，O是正方形的中心，E是正方形AB边的中点，求四边形DEBC的面积。很多学生一看这道题，就会认为这是求不规则多边形面积的问题，他们没学过不规则多边形面积计算的公式，不会做，于是不必思考这个问题了。假如教师先引导学生计算图1中四边形ODBE的面积，学生很快就能计算出：正方形ODBE的边长为1/2，应用正方形面积公式可得面积为（1/2）2=1/4。此时教师将图1旋转成图2，引导学生思考四边形DEBC的面积，学生会意识到，原来将不规则多边形割补了，它就是一个正方形。在这一次的学习过程中，学生掌握了一个几何面积计算的技巧：如果遇到一个不规则的图形，可以应用割补的方法把它变成一个规则的图形再计算。

部分学生的思维能力不足，他们遇到复杂的数学问题的时候，不能应用宏观的、抽象的方法思考问题，得到答案。教师可以从学生理解的基础问题着手，让学生先解出基础问题，再将基础问题变形，引导学生结合基础问题思考数学问题，这时，学生便能理解复杂的、抽象的问题应当如何解决。教师应用这种方法开展教学活动，一方面是培养学生的思维水平，另一方面是积累学生的解题经验。只要学生长期受到这样的训练，思维水平便会逐步提高，解题经验便会逐渐增多。

三、应用创造问题引导学生拓展

教师在开展问题教学时，不能一味地向学生提问题，这会让学生产生错误的学习意识，学生会认为学习知识的目的是为了解答老师提出的问题。教师应在问题教学中鼓励学生主动提出问题、挖掘出更多的知识。

比如教师可引导学生思考以下的问题：如图3，现有三角形木板ABC，BC边为150cm，高AD为100cm，要用木板制作出一个正方形桌面，要求桌面的一边必须在BC边上，这个正方形桌面的最大面积为多少？

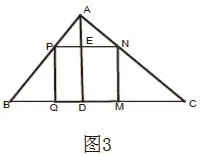
学生结合学过的知识可知因为四边形PQMN是正方形，所以PN∥QM，所以∠ANE=∠ACB=∠ABC。由三角形相似定理可得两个三角形的对应边相等，这两个角相似。结合三角形相似逆定理可知两个三角形对应边的比相等，现设正方形PQMN的边长为xcm，即可得DC/x=AD/（AD-x），将已知条件带入方程可求得x=60。当学生解出这道题以后，教师引导学生思考：现在假设改变这道题的一个已知条件及所求答案，能不能变成另一道题，并且给出这题的答案呢？教师将学生分成学习小组，让学生以小组为单位共同学习。学生在学习的过程中会得到：把正方形桌面变成长方形桌面，求长方形的最大面积；去掉桌面的一边必须在BC边上这个限制，求四边形能截取的最大面积等数学问题。在拓展的过程中，学生的发散思维能够得到培养，在挖掘知识的过程中，学生能感受到探索知识的乐趣。

教师在问题教学中，要引导学生不要被动地等教师提出问题，而应应用发散思维来思考问题，把现有的数学问题变成更多的问题。比如学生可以把问题的一个已知条件或答案改变，把现有的问题变成另一个问题；或者直接去掉一个条件限制，把封闭题型变成开放题型。当学生发现自己可以在学习的过程中创造问题，探索问题时，便能理解学习知识的目的不是为了解答教师提出的问题，而应该是尽可能地探索更多知识，学习更多知识。当学生愿意积极挖掘知识时，他们的发散思维水平便能提升。

教师要设计有趣的数学问题引导学生主动思考问题、应用阶梯式持续提问法培养学生的思维水平、应用鼓励学生创造问题的方法让学生在探索知识的过程中提高发散思维水平。教师应用这样的教学方法，可以激发学生的思维，使学生愿意积极地学习知识，提高学习水平。

[1]王茜.“最近发展区”理论对初中课堂提问的启示[J].赤子（上中旬），2016（20）.

[2]杜印，吴晓莉.走近学生的思维[J].中国农村教育，2014（12）.

[3]李庾南.践行最近发展区 抓住教学着力点[J].中小学教材教学，2015（03）.