煤矿矸石山边坡失稳的滑动位移

尹小军

(1.黑龙江科技大学矿业工程学院，哈尔滨150022; 2.黑龙江科技大学黑龙江省煤矿深部开采地压控制与瓦斯治理省重点实验室，哈尔滨150022)

煤矿矸石山边坡失稳的滑动位移

尹小军1，2

(1.黑龙江科技大学矿业工程学院，哈尔滨150022; 2.黑龙江科技大学黑龙江省煤矿深部开采地压控制与瓦斯治理省重点实验室，哈尔滨150022)

针对煤矿矸石山失稳滑坡问题，基于块体滑动分析法，提出了煤矿矸石山滑坡机理模型。该滑坡模型由两个滑动块体构成。假设滑动体为纯摩擦性材料，滑动过程中体积不发生变化。根据边坡安全因子，选取实际煤矿矸石山的相关参数，计算初始边坡安全因子和滑动过程中的块体位移。利用滑动块体安全因子和块体滑移位移可以反演分析任一时刻滑动块体的剪切强度，表明该方法分析煤矿矸石山边坡失稳的可行性。

矸石山;边坡失稳;滑动位移;临界高度

0 引言

随着煤炭生产的持续增加，煤矸石的堆积也迅速增加，形成占地面积广、安全隐患大的矸石山。我国煤矸石利用率低，存在大量堆放不规范的矸石山，各地矸石山时有垮塌、滑坡及泥石流事故发生，造成生命财产的巨大威胁和损失。因此，矸石山环境地质灾害的防治相当重要。邓丁海等［1］指出矸石山堆积基础岩土体的抗剪强度特性、矸石山自身结构和基础岩土体孔隙水压力、堆放矸石区的地表斜率、矸石山堆积高度以及它周边的边坡角等因素控制矸石山的稳定性。董倩等［2］利用极限分析上限法研究了矸石山的稳定性。廉荣峰［3］结合煤矿矸石山实例，分析了煤矿矸石山稳定性问题，提出了矸石山滑坡灾害防治措施。Bishop A W等［4］引入边坡安全因子F，作为分析边坡稳定的指标，安全因子为抗滑力与滑动力的比值或抗滑力矩与滑动力矩的比值。当F大于1时，边坡稳定;等于1时，边坡处于临界状态;小于1时，边坡失稳。然而，在大量工程实践中，当安全系数F小于1时，边坡仍然是稳定的。许多研究人员［5－10］用块体法分析了边坡稳定性问题，该方法是通过块体滑动位移来分析边坡稳定性。但对于煤矿矸石山的稳定分析，采用块体分析法研究其稳定性以及失稳后滑动位移的研究鲜有报道。文中利用块体分析法，假设滑动块体具有不可压缩性，为纯摩擦性材料，利用牛顿第二定律，通过积分，以求得块体的滑移距离，来计算煤矿矸石山滑移前的初始安全因子和任一时刻的滑动位移。

1 煤矿矸石山边坡模型

1.1 问题定义

煤矿矸石山如图1所示，为了便于分析研究，将实物模型抽象为两个滑动块体的二维平面模型，根据煤矿矸石山的构成特性，假设矸石山块体为纯摩擦性材料，则滑动过程中黏聚力c=0，内摩擦角δ≠0。

图1 煤矿矸石山Fig.1 Coal gangue

1.2 边坡滑移模型

模型由两个滑动块体组成，上部滑动块体为四边形EBCD，下部滑动块体为三角形BCA，如图2所示。上部滑动体的倾角为α1、滑面长度为L、宽度为b、下部滑动体的倾角为α2、滑面长度为l、两个滑块的交界面为BC，交界面的夹角为β(记角逆时针为正，角顺时针为负，滑动过程中块体剪切强度由峰值降低，用α表示衰减系数)。设上部滑块的滑动位移为u1，下部滑块的滑移位移为u2，两块体之间的相互作用力为p。

2 煤矿矸石山边坡失稳分析

2.1 单元块体计算分析

根据牛顿第二定律，分别列出两个块体在t时刻的运动方程。

第一个块体的运动方程:

第二个块体的运动方程:

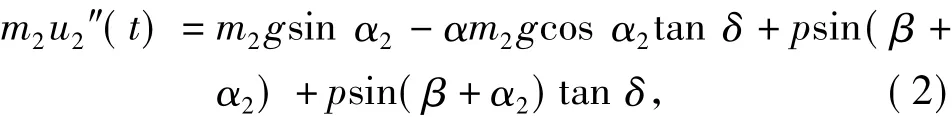
其中:

假设矸石山块体滑移过程中体积不变，即具有不可压缩性，则两滑动块体位移具有下列关系:

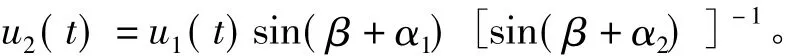
2.2 滑动块体内力求解

组合方程式(1)和(2)，可求得块体的内力p，

2.3 滑动块体位移求解

将式(3)带入式(1)，可求得位移表达式:

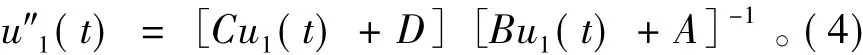
在式(4)中，各参数如下:

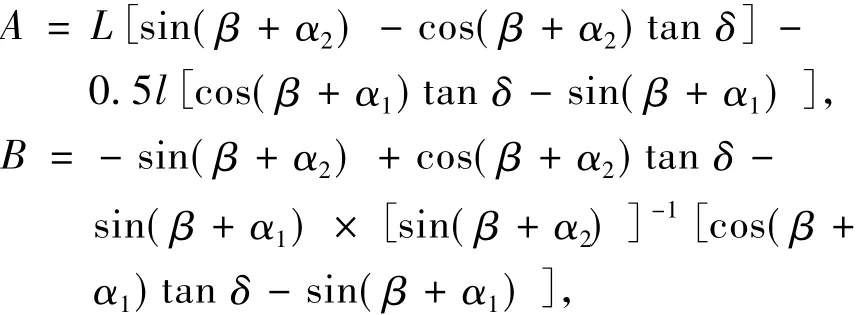
通过积分，可求得在任意时间t内的u1″(t)、u1'(t)和u1(t)。

2.4 安全因子分析

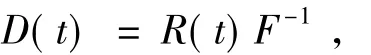
矸石山滑动块体的滑动力:

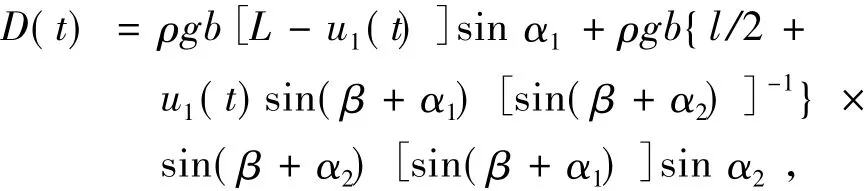
矸石山滑动块体的抗滑力:

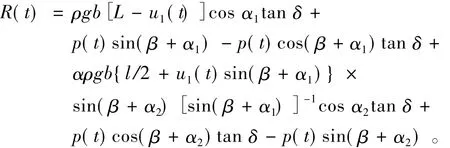
矸石山块体滑动之前的安全因子，即初始安全因子:

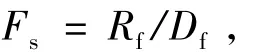
其中，Df=D0，Rf=R0+cL+αcl。

根据假设，则得到式(5):

在时间t=0时，u(t)=0，式(5)可化为:

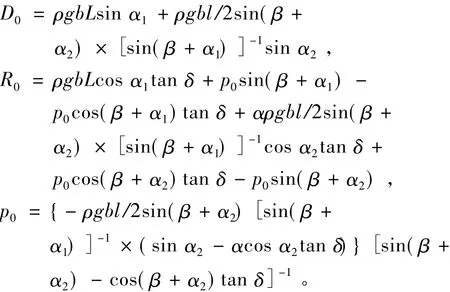
3 结果与分析

应用Matlab软件，通过编程，利用方程(5)，可求得初始安全因子。简化方程式(4)，可求得特殊情况下(u1=u2)的滑动块体的位移。计算模型所采用的物理参数如表1所示。

表1 计算模型所采用的物理参数Table 1 Physical parameters of computing model

3.1 初始安全因子分析

图3为考虑剪切强度衰减时(0＜α＜1)初始安全因子的变化情况。图4为初始安全因子随交界面夹角的关系。

图3 初始安全因子随衰减系数的关系Fig.3 Variation relationship of initial factor of safety with attenuation coefficient

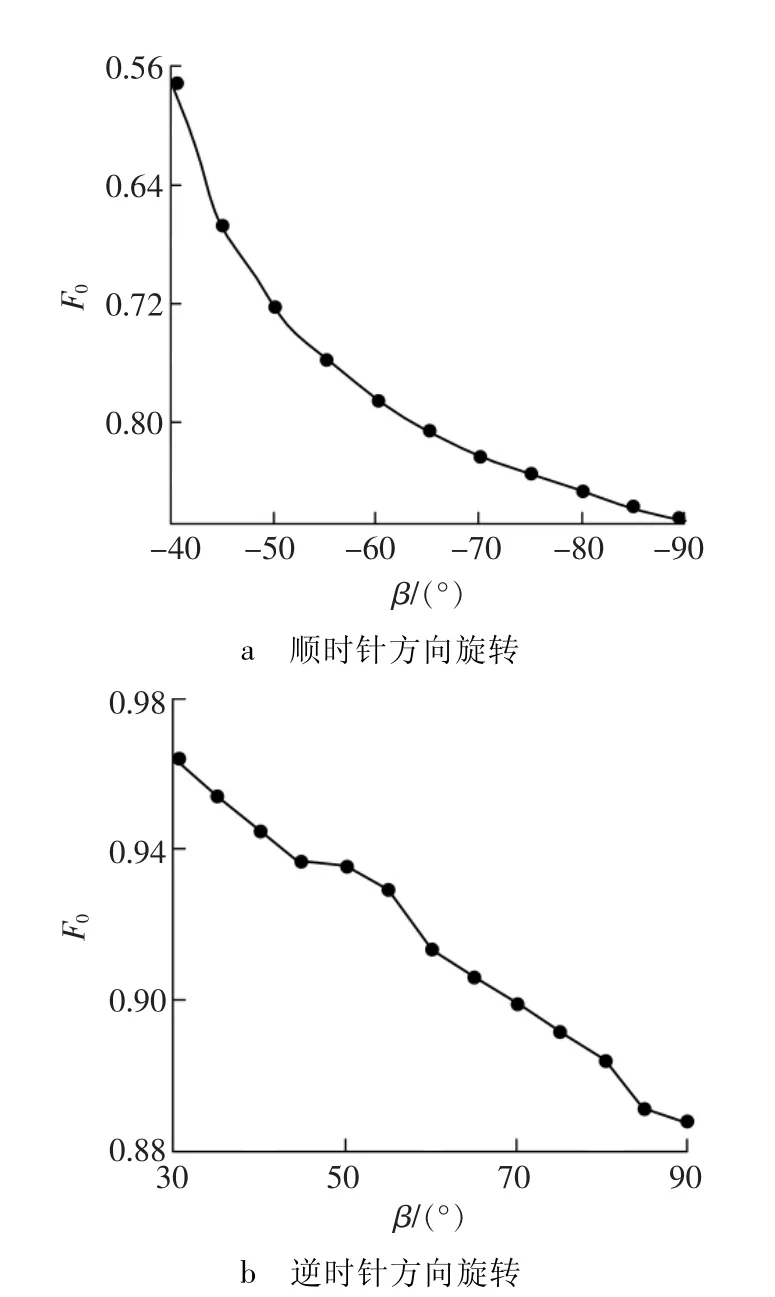
图4 初始安全因子随交界面夹角的关系Fig.4 Variation relationship of initial factor of safety with masses intersected angle

由图3可知，安全因子与矸石山滑动块体剪切强度的衰减系数基本成线性关系;在很多分析中，一旦边坡失稳，则将其剪切强度取为残余值，实际上是一个逐渐衰减过程，通过该分析，表明剪切强度值的衰减也是影响边坡稳定的一个重要因素。

由图4可见，顺时针方向旋转时，安全因子随滑动块体的倾角减小而增加;逆时针方向旋转时，安全因子随滑动块体的倾角增加而减小。通过以上分析可知，当两滑动块体的交界面倾角不同时，对边坡初始安全因子的影响是各不相同的，在一定倾角范围内甚至变化很大;也说明了这一事实，即在节理岩体中，裂隙面倾角不同，边坡的稳定性不同。

3.2 滑动块体位移分析

求解方程式(4)，可得滑动块体的位移，在不同情况下，求解的位移各不相同。研究中只考虑u1=u2时，滑动块体的位移，此时方程简化为

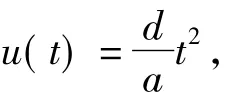
其中，t是矸石山块体滑动的时间，a=L+0.5l，d=gL(sin α1－cos α1tan δ)+0.5gl(sin α2－αcos α2tan δ)。

图5为不同倾角下滑动块体位移与时间的关系。

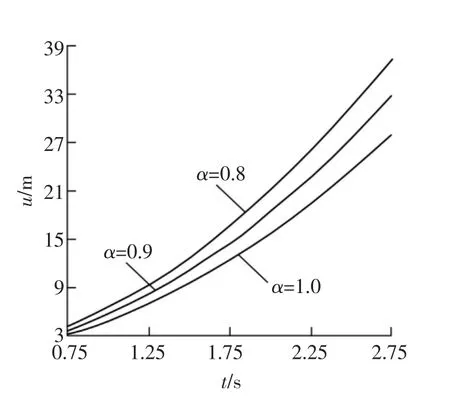
图5 滑动块体位移与时间的关系Fig.5 Displacements of sliding masses relationship with times

由图5可见，滑动块体位移随时间的增加迅速增加，当矸石山滑动块体剪切强度变化系数减低后，位移增加，t为1和3 s，α=1的位移与α=0.8的位移变化分别为74.9%和85.71%。而通过块体滑动位移的大小来判断矸石山的稳定性，比单纯的安全因子更加可靠。同时，矸石山块体滑动位移究竟多大会失稳，需要观察大量实际矸石山失稳数据来界定，是一个需要深入研究的课题。

4 结束语

通过对煤矿矸石山的分析，给定相应的条件，提出了煤矿矸石山滑动的边坡模型。利用块体分析法，求解了矸石山滑动的边坡初始安全因子。利用所得位移表达式，给出了特殊情况下在任一时刻滑动块体的位移。研究结果表明:根据滑动块体位移，可以反演分析在任一时刻滑动块体的剪切强度;根据已求解的初始安全因子，利用滑动位移，可求得在该时刻的滑动安全因子。该研究可为矸石山提供一种可行的稳定分析方法和稳定性的维护依据。

［1］ 邓丁海，岑文龙.煤研石堆放区的环境效应研究［J］.中国矿业，1999，8:87－91.

［2］ 董 倩，杨东燕.矸石山稳定性非线性极限分析上限法［J］.煤炭学报，2007，32(2):131－135.

［3］ 廉荣峰.南桐煤矿矸石山滑坡灾害防治工程［J］.中国新技术新产品，2012，5:59－60.

［4］ Bishop A W，Morgenstern N R.Stability coefficients for earth slopes［J］.Geotechnique，1960，10(4):129－150.

［5］ Newmark N M.Effects of earthquakes on dams and embankments［J］.Geotechnique，1965，15:139－159.

［6］ Stamatopoulos C，Mavromihalis E，Sarma S K.The effect of geometry changes on sliding-block predictions［C］//Fifth International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics，2010:1－10.

［7］ Constantine A，Constantine M，Sarada S.Correction for geometry changes during motion of sliding-block seismic displacement［J］.Journal of Geotechnical and Geoenvironmental Engineering，2011，137(10):1－14.

［8］ Utili S.Investigation by limit analysis on the stability of slopes with cracks［J］.Geotechnique，2013，63(2):140－154.

［9］ Michalowski R L.Stability assessment of slopes with cracks using limit analysis［J］.Canadian Geotechnical Journal，2013，50(1): 1011－1021.

［10］ Cheng X，Mao N，Xie R，et al.Investigation on the stability of slopes with cracks subjected to seismic effect［J］.Electronic Journal of Geotechnical Engineering，2014，19:4667－4674.

(编校 王 冬)

Sliding displacement of slope instability of coal gangue

Yin Xiaojun1，2
(1.School of Mining Engineering，Heilongjiang University of Science＆Technology，Harbin 150022，China; 2.Heilongjiang Ground Pressure＆Gas Control in Deep Mining Key Lab，Heilongjiang University of Science＆Technology，Harbin 150022，China)

This paper is a response to the instability of coal gangue rock，one of the major safety problems in mining areas and proposes a new model behind coal gangue sliding，composed of two sliding blocks，based on the block sliding analysis method.Given that the blocks are purely friction material，the research points to no change in the volume of blocks during sliding.The study building on the slope factor of safety involves selecting the relevant parameters of the actual coal gangue and thereby calculating the initial slope safety factor and the displacement of the blocks during the sliding process.The inversion analysis of the shear strength of sliding blocks in any time using the factor of safety and the sliding displacement of the blocks verifies the feasibility of this method in analyzing the coal gangue.

coal gangue;slope unstability;sliding displacement;critical height

10.3969/j.issn.2095－7262.2017.04.016

TD824.7

2095－7262(2017)04－0400－04

:A

2017－05－04

尹小军(1980－)，男，甘肃省秦安人，讲师，博士研究生，研究方向:工程岩体稳定性分析及数值模拟，E-mail:yinxiaojun800@ 126.com。