管道输送煤泥快速清淤的固液两相流规律的数值模拟

郝传波， 蒲文龙

(1.黑龙江科技大学，哈尔滨150022;2.黑龙江科技大学安全工程学院，哈尔滨150022)

管道输送煤泥快速清淤的固液两相流规律的数值模拟

郝传波1， 蒲文龙2

(1.黑龙江科技大学，哈尔滨150022;2.黑龙江科技大学安全工程学院，哈尔滨150022)

针对矿井水灾煤泥淤积堵塞巷道影响应急救援时效的关键问题，提出“应急排水－快速清淤”同步救灾新模式。该模式基于固－液两相流及颗粒动力学理论，利用Gambit三维建模和划分网格，选择欧拉模型，运用Fluent软件模拟了不同煤泥质量分数、管径及倾角条件下的固液两相流体规律。结果表明:管道输送效率与管径呈负相关、与倾角呈正相关的关系。管径越小，煤泥浆体固体颗粒碰撞、挤压效应影响越大，压降损失越大;倾角越大，管道出口高程越大、总压差越大。最佳管道输送参数宜为管径250 mm、倾角应控制约15°、煤泥浆体小于45%。

矿井;水灾;煤泥;固－液两相流;数值模拟

0 引言

煤泥淤积堵塞巷道是导致矿井水灾应急救援效率低、灾区受困人员死亡的主要原因。我国矿井水灾发生后，绝大多数应急决策是先应急排水再清理淤积巷道，最后施救受困人员。据矿井水灾案例及救援经验，灾区80%受困人员死亡是由于逃生通道受阻救援失效、氧气耗尽所导致［1－2］。因此，矿井水灾快速清淤已成为安全、快速、有效应急救援和施救灾区受困人员的关键问题。基于此，笔者提出“应急排水－快速清淤”同步救灾新思路，改变先排水再清淤的传统救灾程序，其研究成果对提高应急救援时效具有重要的实用意义。

矿井水灾“排水－清淤”同步一体的技术途径，就是通过应急排水管道输送煤泥浆体。为保证管道输送煤泥效率，防止管道输送过程中煤泥沉淀淤积，必须对管道输送煤泥浆体快速清淤的固液两相流动性规律进行研究。当前，研究固液两相流体管道输送特性的手段为室内试验和数值模拟。由于固液两相流动特性极其复杂，室内环管实验测试流动参数难度大(如无法得到管道内部浆体压力分布和速度分布状况)且成本高，获得实验数据有限，故建立的经验关联式应用范围受到限制［3］。随着计算机软件的发展和不断完善，运用数值模拟分析计算固液两相流体已成为一种全新的研究手段。邓代强等［4］运用Fluent软件对料浆长距离管道输送问题进行了细致分析，张钦礼等［5］结合因次分析法和数值模拟软件对高浓度超细全尾砂料浆的管道输送阻力问题进行了分析。李石林［6］等运用固液两相流的数值模拟方法研究了黏土胶结浆体管道输送特性。郝传波［7］等运用Fluent软件模拟了输送管道为水平状态、管径为150 mm条件下的不同煤泥质量分数的固液两相流体规律。纵观相关研究文献，针对矿井水灾煤泥堵塞淤积巷道条件下，“应急排水－快速清淤”管道输送的固液两相的数值模拟研究鲜有报道。

1 计算模型

1.1 基本假设

由于煤泥管道输送工艺及其流动特性的复杂性，当前仍无法求得管道输送问题的精确解。为方便建模和计算，因此，建模和分析计算时通常假设［8］:(1)在管道输送时将煤泥浆体视为均质满管流而且固体颗粒不发生相变引;(2)将煤泥浆体视为非牛顿流体，流变模型则近似于宾汉姆体，视其流动不可压缩定常流处理;(3)将煤泥浆体的豁性视为恒定，即其不随时间和温度变化;(4)煤泥浆体的管道输送过程不考虑其热量的交换;(5)煤泥浆体的管道输送不受振动和地压波等的影响。

1.2 模型选择

描述流体运动主要有拉格朗日和欧拉法。欧拉法应用较为广泛，能从整个流场的角度分析流速和压强的变化规律，本研究选用欧拉法。在FLUNT中，共有3种多相流模型，即流体体积模型(VOF)、混合模型(Mixture)和欧拉模型(Eulerian)，其中混合物模型可用于两相流或多相流［9］。欧拉模型适合流体中相的混合和分离，精度较高，适合模拟煤泥和水的固液两相。

1.3 控制方程

基于以上假设，煤泥浆体两相流满足流体动力学的理论，即符合三大守恒定律，即质量守恒定律、动量守恒定律和能量守恒定律［10－11］。

(1)质量守恒方程

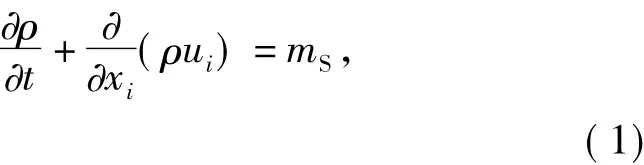
式中:ρ——密度，kg/m3;

t——时间，s;

ui——方向上的速度分量，m/s;

xi——i方向上的位移，m;

mS——质量源项，即从分散的二级相中加入到连续项的质量，kg。

(2)动量守恒方程

式中:uj——i方向上的速度分量，m/s;

xj——j方向上的位移，m;

τij——应力张量，N/m3;

gi——i方向上的重力，N;

Fi——i方向上的外部体积力，即重度(包含了模型的其他相关量)，N/m3。

(3)能量守恒方程

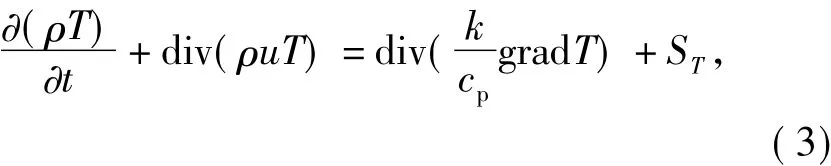
式中:T——温度，K;

u——速度，m/s;

cp——比热容，J/(kg·K);

k——流体的传热系数，W/(m2·K);

ST——能量源项，即流体的内热源及由于黏性作用流体机械能转化为热能的部分，J。

1.4 几何模型及边界条件

煤泥浆体管道输送的数值模拟采用建模软件Gambit进行三维建模和划分网格，采用流体力学软件Fluent计算，如图1、2所示。

图1 管道输送模型Fig.1 Pipeline model

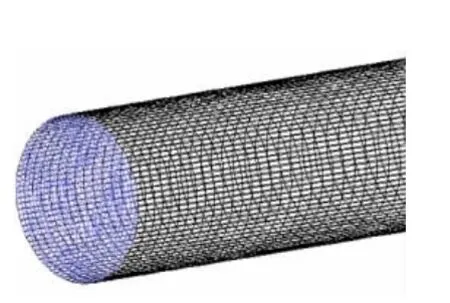
图2 网格划分Fig.2 Meshing

由图1、2可知，管道运输长度为2 m，管道进口速度为流速 v0=1.5 m/s;设置煤泥颗粒密度1 400 kg/m3，煤泥粒径0.25 mm，考虑固相可压缩极限的局部最密体积分数控制在70%以内。

2 Fluent数值模拟与分析

煤泥管道输送规律与煤泥浆体固体颗粒大小、温度、管径、倾角及煤泥浆体浓度等有密切关系。笔者是在水平管道煤泥浆体固液两相流输送规律研究基础上［7］，进一步对不同管径、不同倾角条件下，模拟分析管道输送煤泥浆体的固液两相流体分布规律。

2.1 不同管径流场规律

2.1.1 数值模拟

数值模拟了煤泥质量分数分别为25%、35%、45%、55%、65%条件下不同管径(D=150、200、250 mm)的固体颗粒流场、压强及流速的变化规律。由于篇幅受限，文中只展示管道倾角为30°、煤泥体积分数为55%的模拟结果。中截面体积分布见图3，横截面体积分布见图4，中截面静压力(出口压力为0)见图5，中截面流速见图6。

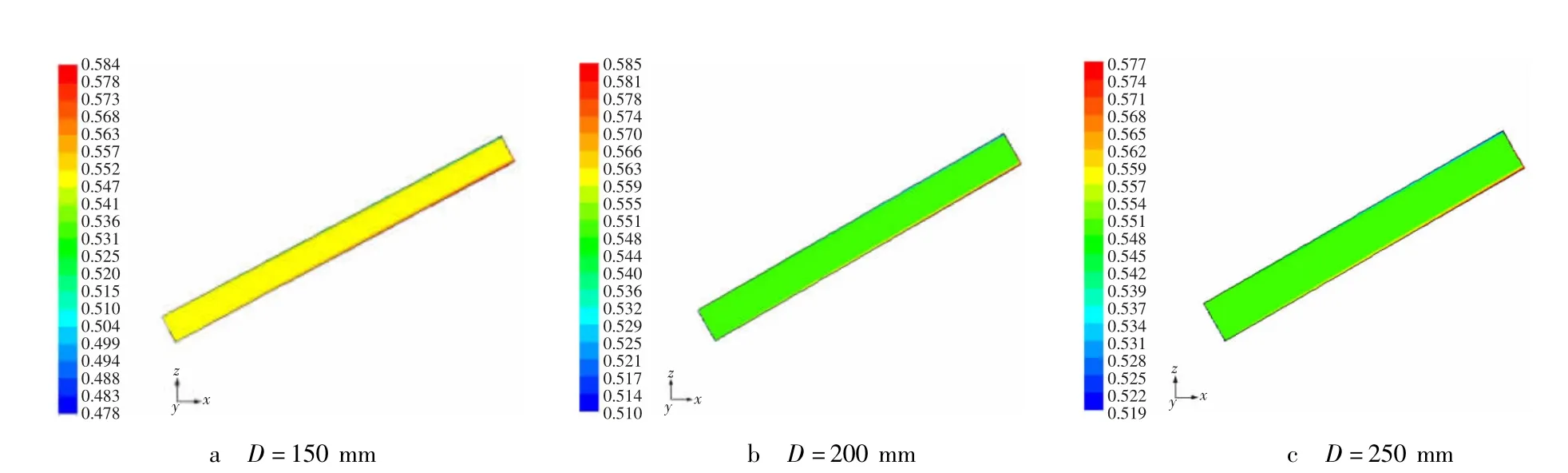
图3 不同管径中截面体积分布Fig.3 Distribution of volume fraction in different pipe diameter

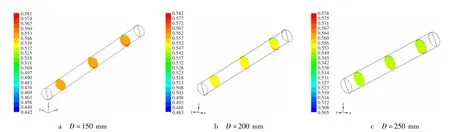
图4 不同管径横截面体积分布Fig.4 Distribution of volume fraction of cross section of different pipe diameters

图5 不同管径中截面压力分布Fig.5 Distribution of cross section pressure in different pipe diameters

图6 不同管径中截面流速分布Fig.6 Flow velocity distribution in different pipe diameter

2.1.2 结果分析

通过数值模拟分析，获得三种不同管径条件管道输送煤泥浆体中的固体颗粒流场、压强及流速分布规律。

(1)由图3可知，不同管径下流场随体积分数变化的主要趋势，在同一浓度条件下，随着管径增大，中截面固体颗粒流场浓度有所下降。这是由于管径增大后，颗粒间距较大，颗粒的湍流脉动，尚不足以引起高频度的颗粒碰撞、摩擦、挤压。

(2)由图4可知，同一浓度浆体沿竖向趋势为，在管道进口处颗粒分布均匀，而在管道后程受颗粒重力影响，最顶部颗粒浓度减少、底部增大;随着管道直径增大，无论顶部颗粒浓度和底部颗粒浓度分布趋势都逐渐减弱。这是由于管道直径增大后的空间释放效应导致的。总之，由颗粒浓度场的云图总体形态可知，管道直径增大后，固体颗粒质量分数的极大值比原来略小(仅在较低质量分数时)，而极小值均比原来略大。这同样是管径的空间释放效应，使得颗粒浓度在总体上比原来平均。

(3)随着煤泥浆体输送管道直径逐渐增大，对应某特定煤泥质量分数的管道进出口压差减小。这是由于管道直径增大的径向空间释放导致而成，即随着管道直径增大，原来越靠近管壁的煤泥固体颗粒越明显的挤压效应会减弱，地层划分及参数见表1。不同浓度区间与管径及压差变化关系见表2。

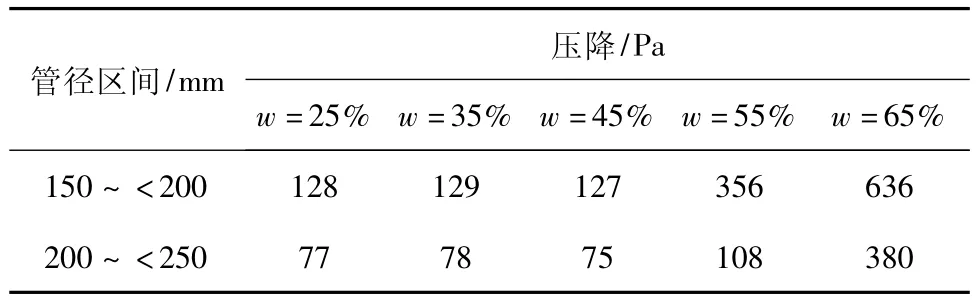
表1 地层划分及参数Table 1 Classification and parameters of strata

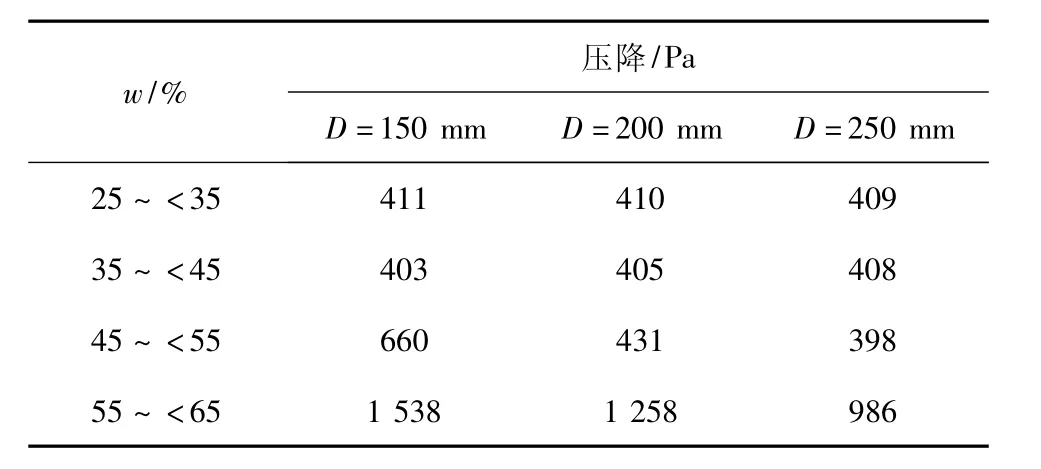
表2 不同浓度区间与管径及压差变化关系Table 2 Relationship between different concentration interval and tube diameter and pressure difference

由表1可知，在质量分数较低时(w为25% ～45%)，管径在150～200 mm和200～250 mm区间，压降分别为1和2 Pa，压差降低幅度比较小且比较稳定;当质量分数较高时(w为55%～65%)，管径在150～200 mm和200～250 mm区间，压降分别为280和272 Pa，下降幅度明显增大，说明空间释放的效果更明显。另外，输送管道直径同样增大50 mm条件下，管道直径由200 mm增大至250 mm对其压差的影响，就没有管道直径由 150 mm增大至200 mm那么明显，说明管径越小其压差越受到煤泥浆体固体颗粒碰撞、挤压效应的影响。

由表2可知，各组相邻上下两级煤泥质量分数间的压差增加幅度，在煤泥低质量分数区间(w= 25%～45%)，不同管径的对应值在400 Pa左右，压降为1 Pa，变化幅度非常小，说明该值仅是平均密度提升引起的增量部分;在煤泥高质量分数区间(w为45%～65%)，随着管径增大其对应压差值下降幅度较大，说明管道空间释放效应抵消了一部分压力差值。

2.2 不同管道倾角流场规律

2.2.1 倾角模拟

分别模拟了煤泥质量分数为25%、35%、45%、55%、65%条件下不同倾角的固体颗粒流场、流速及压强的变化规律。由于篇幅受限，文中只展示煤泥质量分数为55%、管径为150 mm的模拟结果。中截面体积分布见图7，横截面体积分布见图8，中截面静压力(出口压力为0)见图9，中截面流速见图10。

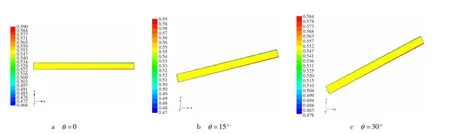
图7 不同倾角中截面体积分布Fig.7 Distribution of sectional volume fraction in different inclinations

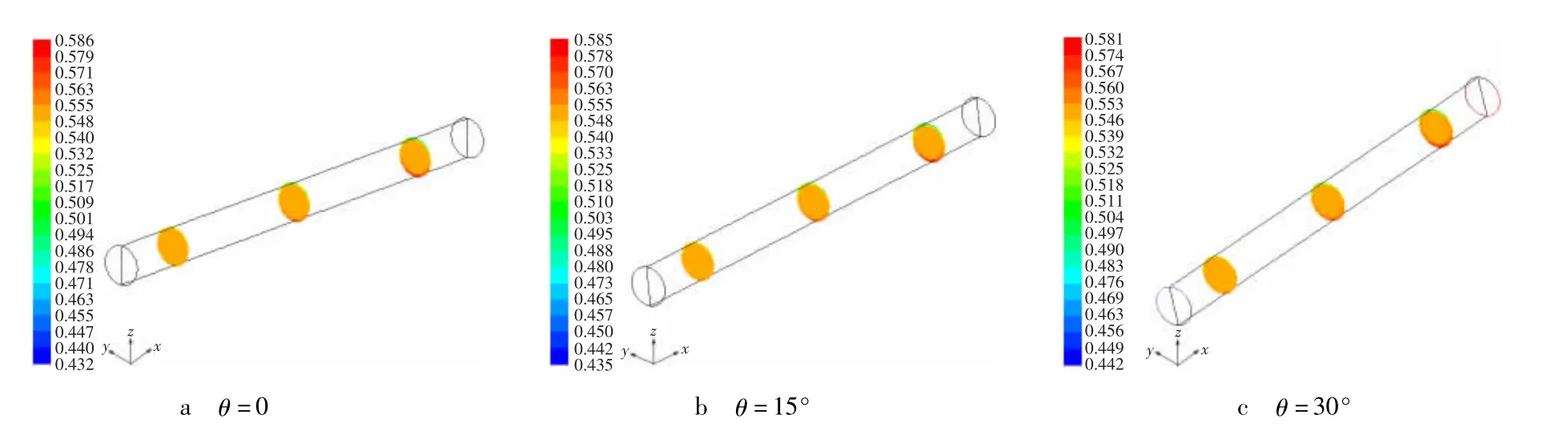
图8 不同倾角横截面体积分布Fig.8 Distribution of volume fraction of cross section of different inclinations

图9 不同倾角中截面体积分布Fig.9 Distribution of sectional volume fraction in different inclinations

图10 不同倾角横截面体积分布Fig.10 Distribution of volume fraction of cross section of different inclinations

2.2.2 模拟分析

通过数值模拟分析，获得三种不同倾角管道输送煤泥浆体中的固体颗粒流场、压强及流速分布规律。

(1)由图7和图8可知，倾角改变前后颗粒浓度场的图片总体形态还比较相似;区别在于，管道倾角增大后，固体颗粒质量分数的极大值比原来略小，极小值比原来略大。其原因是，当管道从水平趋近于垂直时，颗粒沿管道横向的沉降效应会减弱，浓度沿轴线两侧的对称度会有提高。

(2)由图9可知，随输送管道倾角增大，压力场的变化最为明显。因为出口高程的增加，需要克服输送物料的重力势能，进口压力自然大幅提高，倾角越大，总压差越大。管道倾角越大，沿轴向均匀产生的用以克服重力的沿程阻力越占主导地位，而沿径向平面的沉降效应所占比例越小，压力等高线也会越接近于与管轴线垂直。

(3)对于各组相邻上下两级质量分数间的压差增加幅度，θ=15°时比θ=0°时多200 Pa左右;θ= 30°时比θ=15°时约多190 Pa。可见，压差增幅中，因颗粒密度上升造成碰撞、挤压能耗变化部分和管道倾角几乎无关，多出来的部分，是因倾角加大引起提升高程增加造成的，见表3。

表3 不同区间及倾角与压差关系Table 3 Elationship between different concentration interval and dip Angle and pressure difference

(4)通过模拟云图获得不同倾角下不同质量分数管道压降变化值(见表4)，获得其压降曲线变化规律。由图11可知，随着管道倾角增大，压降损失也增大;同一管道倾角下，煤泥浆体质量分数小于45%时压降损失幅度较小，当浆体质量分数大于45%时压降损失幅度较大。因此，为提高煤泥管道输送效率，浆体应小于45%。由于煤矿井下救灾现场巷道并非水平状态，因此，输送管道倾角宜控制在15°左右，不宜太大，否则压降损失更大。

表4 不同管道倾角下不同质量分数管道压降Table 4 Pressure drop of different volume fraction underdifferent pipe inclinations

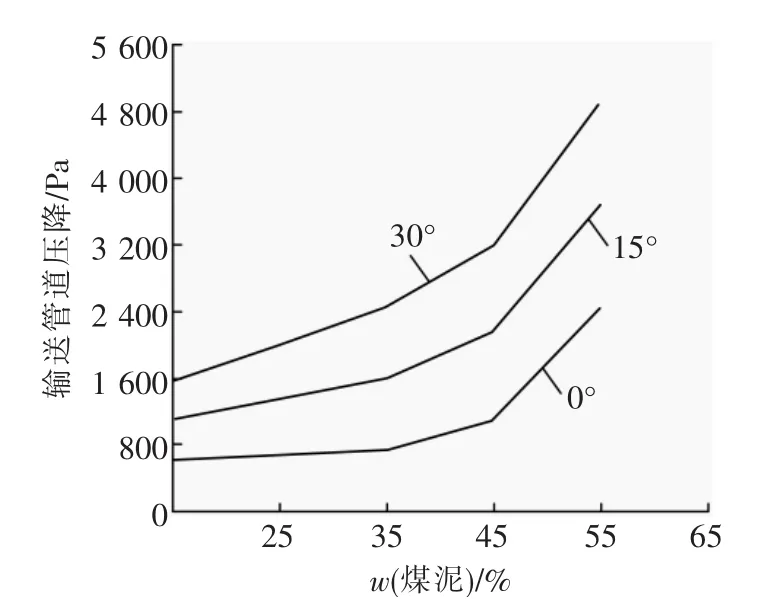
图11 不同管道倾角条件下煤泥质量分数与压降之间变化规律Fig.11 Changes of quality fraction and pressure drop under different pipe inclination conditions

3 结论

针对矿井水灾煤泥淤积堵塞巷道影响救援时效关键问题，笔者提出“应急排水－快速清淤”同步救援模式，运用FLUNET模拟分析了不同煤泥浆体浓度、管径与倾角对管道输送固液两相流体规律，结论如下。

(1)不同管道直径下的煤泥浆体流场规律:随管道直径逐渐增大，某特定质量分数的进出口压差减小。这是由于管道径向空间释放，靠近管壁挤压效应减弱所致。这种压差降低在质量分数较低时幅度比较小且比较稳定，当质量分数较高时则幅度明显增大。

(2)不同管道倾角下的煤泥浆体流场规律:随管道倾角增加，其出口高程也增大，进口压力自然大幅提高。随倾角越大总压差越大，沿轴向用以克服重力的沿程阻力越占主导地位，而沿径向平面的沉降效应所占比例越小，压力等高线也会越接近于与管道轴线垂直。

(3)为提高管道输送煤泥快速清淤效率，煤泥质量分数应小于45%，管道倾角约15°，管径选择250 mm最佳，否则压降损失较大。另外，为提高清淤时效，防止管道堵塞，可充分搅拌煤泥浆体增加管道进口流速。

［1］ 郝传波，刘永立.煤矿事故应急救援典型案例分析［M］.北京:煤炭工业出版社，2016.

［2］ 郝传波，张国华.煤矿井下灾后救援中垮塌巷道研究的展望［J］.黑龙江科技学院学报，2012，22(6):549－552.

［3］ 曹志先，魏良琐，谢鉴衡.明渠挟沙水流的两相流模式［J］.水利学报，1995，(4):1－12.

［4］ 邓代强，朱永建，工发芝.充填料浆长距离管道输送数值模拟［J］.安徽大学学报(自然科学版)，2012，36(6):36－43.

［5］ 张钦礼，姜志良，工 石.高浓度超细全尾砂充填料浆管道输送阻力模型［J］.科技导报，2014，32(24):51－55.

［6］ 李石林，冯 涛，工鹏飞.粘土胶结充填浆体管道输送特性试验与数值模拟研究［J］.安全与环境学报，2013，13(6):73－76.

［7］ 郝传波，蒲文龙，张国华.矿井“应急排水－快速清淤”的固液两相流数值模拟［J］.黑龙江科技大学学报，2017，27(1):8－12.

［8］ 刘大有.二相流体动力学［M］.北京:高等教育出版社，1993.

［9］ 倪晋仁，王光谦，张红武.固液两相流基本理论及其最新应用［M］.北京:科学出版社，1991.

［10］ 谢振华，宋存义.工程流体力学［M］.北京:冶金工业出版社，2009.

［11］ 李进良，李承曦，胡仁喜.精通FLUENT6.3流场分析［M］.北京:化学工业出版社，2009.

(编辑 晁晓筠 校对 李德根)

Simulation of law underlying solid liquid two-phase flow for rapid desilting of coal sludge in pipeline transportation

Hao Chuanbo1， Pu Wenlong2
(1.Heilongjiang University of Science＆Technology，Harbin 150022，China; 2.School of Safety Engineering，Heilongjiang University of Science＆Technology，Harbin 150022，China)

This paper is aimed at addressing the key problems of how flood coal sludge in mine flood affects the emergency relief of the roadway and proposes the new mode of synchronous disaster relief:emergency drainage-rapid desilting.The study based on solid-liquid two-phase flow and particle dynamics theory is focused on using Gambit of 3D modeling and mesh to choose the eulerian model and using Fluent software to simulate the different coal volume fraction，the diameter and angle under the condition of solid-liquid two-phase fluid.The results show that the efficiency of pipeline is negatively correlated with pipe diameter and positively correlated with dip angle，suggesting that the smaller diameter contributes to a greater effect on the collision and squeezing of coal slurry solid particle，with the resultant greater pressure drop loss;the larger tilt angle leads to the larger outlet elevation and the greater total pressure difference;the optimum parameters of the pipeline are:the pipe diameter is preferably 250 mm，dip angle should be about 15°，and the concentration of coal slurry should be below 45%.

mine flood;coal slime;solid-liquid two-phase flow;numerical simulation

10.3969/j.issn.2095－7262.2017.04.008

TD745

2095－7262(2017)04－0359－07

:A

2017－05－14

国家自然科学基金项目(51374097;51674107)

郝传波(1962－)男，黑龙江省宁安人，教授，博士生导师，研究方向:煤矿应急救援与外向控制、矿山安全管理，E-mail:haochuanbo@126.com。