基于多变量干扰观测器－控制器综合的再入姿态控制

侯睿哲

（华南理工大学软件学院，广东广州510641）

基于多变量干扰观测器－控制器综合的再入姿态控制

侯睿哲

（华南理工大学软件学院，广东广州510641）

针对高超声速飞行器的再入姿态控制问题，分别在全状态反馈和输出反馈的框架内，研究基于多变量干扰观测器－控制器综合的再入姿态控制策略，实现系统在不确定及外界干扰综合影响下对给定制导指令的高精度快速跟踪研究，并在Matlab／Simulink中进行仿真校验.通过仿真结果可以得出，基于输出反馈的干扰观测器－控制器对干扰有较好的响应，可以在遇到干扰时快速跟踪上期望值并保持稳定.

再入飞行器；干扰观测器－控制器；全状态反馈与输出反馈

高超声速再入飞行器是一种新型的航空航天飞行器，正在蓬勃发展，具有重要的军事价值和民用价值.目前，世界航空航天大国都将设计经济且可重复使用的飞行器（RLV）作为未来的太空任务，从而降低进入太空的成本.为此，已经提出许多先进的控制技术以提高飞行器的安全性和可靠性.然而，再入姿态控制系统设计面临的最大的挑战在于飞行器模型受到大量的外界干扰和模型参数不确定的影响，导致模型呈现出异常复杂的非线性和不确定性，加剧了控制器设计的难度.此外，飞行器模型有较高的非线性、强耦合的特性，使得姿态控制器的设计困难较多.在最近几年，相关专家已经进行了大量的工作，以开发先进的姿态控制算法，从而弥补再入姿态系统的不确定性和干扰性.笔者提出一种基于多变量控制器和干扰观测器再入姿态控制方案，使得系统在受到不确定和干扰综合影响的前提下，实现对给定参考指令的高精度快速跟踪.

1 再入姿态模型分析和问题描述

在飞行器的再入姿态控制中，主要是对飞行器的俯仰角、滚转角、偏航角这三项的角度与角速率进行控制，俯仰角、滚转角、偏航角是描述导弹（或飞机）在惯性坐标系中的姿态，这三个角也称为欧拉角.

偏航角定义为导弹OY轴在水平面上的投影与地面坐标Oy轴（在水平面上，指向目标为正）之间的夹角，由OY轴逆时针转至导弹纵轴的投影线时，偏航角为正，反之为负.俯仰角，顾名思义，是导弹（或飞机）相对于XOY平面的惯性坐标系“间距”的角度.对于导弹（或飞机），确定导弹（或飞机）在空间中的方向需要三个角度，分别为偏航角、俯仰角和滚转角.

飞行器再入姿态的方程式描述如下：

图1 欧拉角坐标系

其中，Θ＝［αβδ］代表飞行器的三个姿态角矢量，攻角、侧滑角和侧倾角；ω＝［pqr］代表三个偏转角的角速率矢量，M＝［MXMYMZ］代表控制输入矢量，俯仰、滚转和偏航力矩；非匹配的干扰ΔF是由于模型简化而导致的不确定干扰；ΔM是由于外部扰动导致的干扰力矩.矩阵I，R，Ω∈R3×3定义［1］如下：

2 积分链系统的全状态反馈控制器设计

首先进行再入控制系统的设计，为表述方便，先针对标称的多变量积分链系统进行控制器和干扰观测器的设计.

本文的主要结果可归纳为如下定理：

定理1 考虑如下的多变量积分系统：

其中，x1＝x11，...，x1m

［］T，x2＝x21，...，x2m［

］T是系统的状态向量，而u是系统的控制向量，如果将控制器u设计为：

且控制参数满足 k1，k2＞0，ρ1＝ρ／（2－ρ），ρ2＝ρ；ρ∈（0，1）时，系统状态变量x1，x2将会在有限时间趋近到0.

证 将李雅普诺夫函数构造成如下形式：

显然，V是一个连续正定的函数，李雅普诺夫函数的导数可表示为

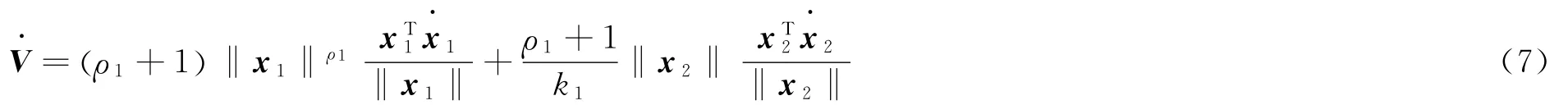
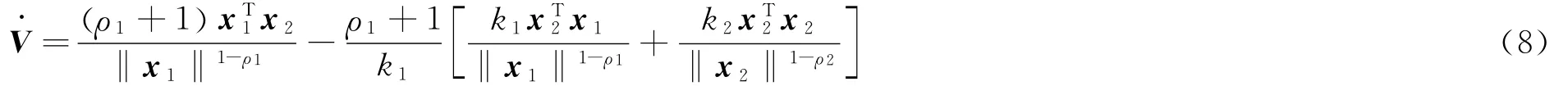
将x1Tx2＝x2Tx1和x2Tx2＝‖x2‖2代入简化可得：

基于干扰观测器所用到的核心算法归纳如下：

引理1［2］考虑如下形式的多变量系统：

其中x＝［x1，...，xm］T是系统的状态向量，而u是系统的控制向量.干扰Δ满足‖‖#δ，其中δ存在但未知.那么，干扰Δ可以在有限时间内通过如下观测器中的z2进行重构：

其中e1＝z1－x，自适应增益kit（）i＝1，2，3，4（

）设计如下：

其中k是正的常数，自适应增益参数cit（）i＝1，2，3，4（

）和初始值L（0）是正的常数，并满足以下条件：

3 再入姿态控制器－干扰观测器综合

为表述方便，定义如下变量：

假设1 假设式（18）中的不确定ΔF和ΔM满足‖Δ·F‖#δ1和‖Δ·M‖#δ2，其中δ1，δ2存在但未知.基于状态反馈的再入姿态控制器－观测器综合控制策略，通过下述定理给出：

定理2 考虑系统（18）在满足假设1的前提下，构造如下控制器

如果控制器参数k1，k2，ρ1，ρ2按照定理1进行选取，ΔM作为ΔM的估计值可以通过引理1提出多变量扰动观测器得到，那么，y1，y2将会在有限时间内趋于0.

证 将式（19）带入到式（18）中，可得：

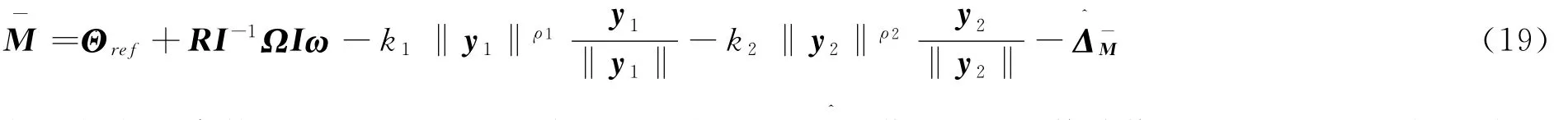
由柯西不等式定理可得，下列不等式成立：

考虑到不等式ab#（a2＋b2）／2对于任何实数a，b都成立，则李雅普诺夫函数导数可转化为：

以下两种情况都能保证V在有限时间内是有界的.

（i）当‖y1‖1时，根据条件1∈0，1（），可以得出不等式21#1＋1，1＋1#2，在式（24）中的李雅普诺夫函数满足：

对于任何连续的k1，由于eF，eM－的有界性，（（（1＋1）［k1‖eF‖2＋‖e‖2］）／（2k1））都是有界的.

（ii）当‖y1‖＜1时，可得‖y1‖21＜1，于是就满足：

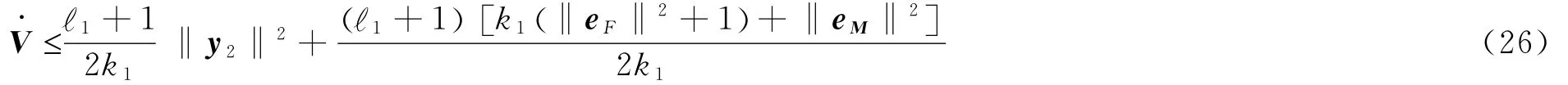
从李雅普诺夫函数导数中可以得出1＋1（）／2k1（）‖y2‖2（

）#V，因此，式（26）可改写为：

由上式，根据定理2，可知eF，eM－会在有限时间内趋于0，而根据定理1，知道y1，y2也会在有限时间内得到确保，由此得证.

在基于全状态反馈干扰观测器－控制器的设计与分析中，由于再入姿态控制器复杂的方程式，涉及角度，角速率和力矩等量［3］.笔者先采用积分链的形式进行推导，从而使定理较为简明，最后加入到控制器的设计，在对定理的整体内容有一定的把握之后，对控制器的设计与推导就会更便于理解.

4 基于输出反馈的再入姿态控制器－观测器综合

在许多实际的飞行器再入姿态系统中，系统的不确定性不通过控制进入输入通道，这些不确定性被称为非匹配的不确定性［4］.非匹配不确定系统的控制器设计是控制理论中最具挑战性的问题之一.

笔者考虑到再入姿态角模块对RLV同时存在匹配与非匹配的干扰，将被描述如下：

其中，Θ＝αβδ［］代表飞行器的三个姿态角矢量，俯仰角、滚转角和偏航角；ω＝pqr［］代表三个偏转角的角速率矢量，M＝MXMYMZ［］代表控制器矢量，俯仰、滚转和偏航力矩；ΔF，ΔM分别代表着非匹配与匹配的干扰.矩阵I，R，Ω∈R3×3定义如式（3）.

本文主要目的是提出一个输出反馈控制方案，使得系统存在匹配干扰ΔM和非匹配干扰ΔF的同时，在有限时间内实现对给定参考指令的稳定跟踪控制.

为了进行控制器设计，假设高超声速飞行器再入过程中的匹配干扰Δ2和非匹配干扰Δ1满足如下条件：

假设2 推测干扰Δi是连续的并可区分的，满足在i＝1，2和j＝0到3－i.

接下来，进行多变量有限时间控制器和观测器的设计，以达到在前文中所述的目标.具体而言，就是用一种新的多变量有限时间控制器来首先分析双积分系统，然后结合多变量定时观测器，完成再入姿态控制器和观测器的合成.

5 积分链系统的输出反馈控制器设计

定理3 为了进行控制器设计，考虑双积分系统（4）.

如果将（4）中的控制器u设计为：

其中ki＞0，i＝1，2，参数ρi，ρ′i如下：

其中ρ∈0，1（），这样，x1，x2→0将在固定时间内成立.

证 考虑下式中的连续可微的李雅普诺夫函数：

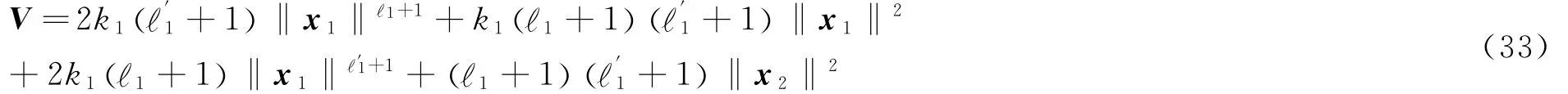
很明显，式（33）中的李雅普诺夫函数V是正定且径向无界的.将式（33）中李雅普诺夫关于时间的导数带入到双积分系统当中，可得李雅普诺夫函数导数如下式：

其中，∏＝21＋1（）′1＋1（）.将（23）和（24）中变量代入，可得重构的李雅普诺夫函数的导数如下：

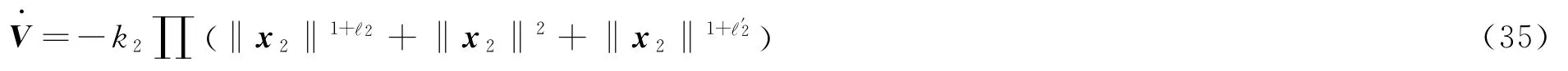
显然，李雅普诺夫函数V在式（33）中是正定且径向无界的，而它的导数V·在式（34）中是负半正定的，当且仅当‖x2‖＝0时，V·＝0.根据LaSalle不变原理，可以得证.同时容易验证，由积分系统和控制律（33）构成的闭环系统是齐次系统且具有负的齐次，则根据既有的研究结论可知，该系统是有限时间稳定的.

6 再入姿态输出反馈控制器－干扰观测器综合

对再入姿态角控制器与观测器的综合，在下面的讨论中，为了简便，介绍如下中间变量：

将式（36）中的变换，代入到式（20）和式（21）中.这样，姿态角模型就将被转化为：

设定姿态角跟踪误差z1＝Θ－Θref，z2＝ω－＋ΔF－Θ·ref是通过观测器预测出来的变量.如果定义ω－，那么系统（39）将被改写为如下形式：

RI－1ΩIR－1ΔF－R·R－1ΔF.随着假设1，可以推测出如下几个假设：

经过上述变换，针对模型（20）（21）的输出反馈再入姿态控制，就等价为对模型（37）设计基于输出反馈的控制器－观测器，使得z1在有限时间内收敛到零，为了实现该目的，笔者提出了如下定理：

定理4 考虑系统（40）在满足假设2和假设3的前提下，如果控制器按照式（39）进行设计，观测器按照式（40）进行设计，则再入姿态跟踪误差z1＝Θ－Θ＊在有限时间内收敛到零.

（1）控制器M－设计如下：

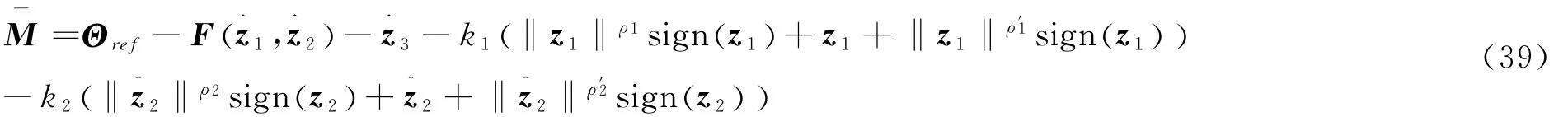
其中ki，ρi，ρ′i，i＝1，2选自定理3.

（2）控制器中的z＾1，z＾2，z＾3是z1，z2，Δ的估计，可通过如下的观测器得到：

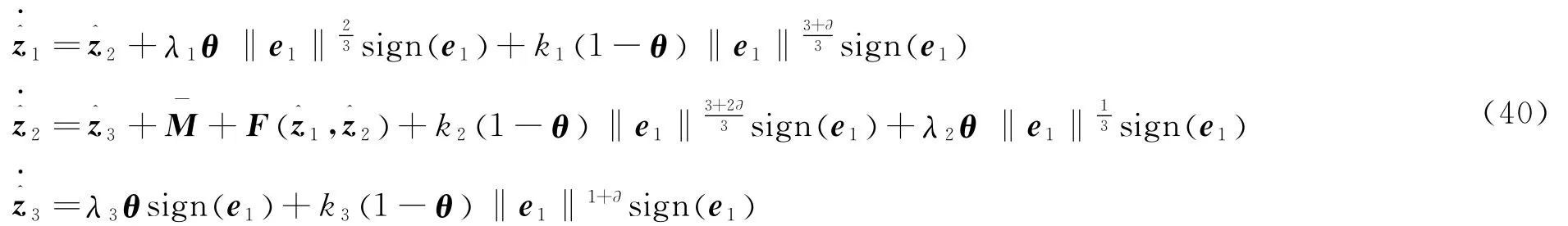
步骤1.用式（40）～式（38），可获得如下的基于观测误差的动力学方程：

步骤2：当估计误差收敛到零后，观测器的参数z＾1估计z1，z＾2估计z2，z＾3估计Δ，此时，将式（39）代入到式（38）可得：

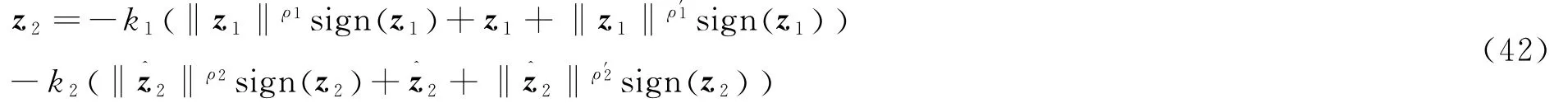
再根据定理1，可知系统是有限时间稳定的，即模型，在控制器（41）和观测器（42）综合作用下，能确保再入姿态在有限时间内收敛到零.

7 输出反馈的仿真及分析

在前文中，通过定理证明与公式推导，在理论上已经具备飞行器再入姿态在有限时间内收敛到零.观测器也能够估计出飞行器角速率的值并在有限时间内误差趋于0.下图为在Matlab／Simulink中进行仿真验证，搭建框图如图2所示：

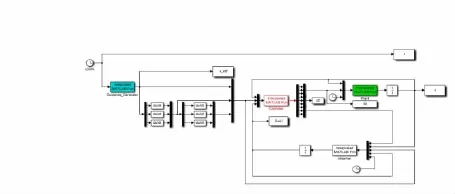
图2 Simuink下的输出反馈再入姿态控制结构框图

飞行器在Matlab仿真中参数设定如下：IXX＝434 270slug·ft2，IXY＝17 880slug·ft2，IYY＝961 220slug·ft2，IZZ＝1 131 541slug ·ft2，IXY＝IYZ＝0slug·ft2控制器参数选择如下：k1＝0.8，k2＝1.2，ρ＝0.6［6］，观测器参数设置为λ1＝16，k2＝12，k3＝4，＝0.1，为方便起见，这里就使用300s作为仿真时长.仿真步长设置为2ms［7］.

由图3可见，系统在干扰始终存在的情况下，能够很快跟踪上期望值并保持稳定.且从图像中很容易发现，飞行器再入阶段系统响应速度很快，能够迅速排除干扰影响，在跟踪上期望值后不存在稳态误差.具有良好的响应.

图3 飞行器攻角、侧滑角、侧斜角随时间变化曲线

由图4可见，系统角速率在干扰始终存在的情况下，也能够迅速跟踪上期望值，在迎角角速率和侧滑角角速率的图像曲线中，实际值一旦跟踪上期望值以后，就能保持稳定，不存在稳态误差.而侧倾角角速率在干扰始终存在的情况下，在跟踪上期望值以后，始终存在着微弱的波动，其稳定性较迎角角速率和侧滑角角速率略微较差.在系统稳定时，再入姿态的角速率都稳定为0.

由图5可见，飞行器控制力矩在干扰始终存在的情况下，曲线随时间一直在不断波动、变化，这是为了保持飞行器再入阶段角度保持稳定而必须的.通过图像可以发现，在干扰刚开始扰动系统时，飞行器控制力矩变化较为剧烈，波动较大，随着时间推进，飞行器控制力矩能够在较小的范围内，平稳的变化，这对保持飞行器再入姿态阶段的稳定，也是必须的.

8 结论

笔者主要对飞行器再入阶段的非线性系统提出方案和分析仿真，在实际情况下的系统，往往要面临着大量的外界干扰和模型参数不确定的影响，导致模型呈现出异常复杂的非线性和不确定特性.笔者提出一种基于多变量控制器和干扰观测器再入姿态控制方案，使得系统在受到不确定和干扰综合影响的前提下，实现对给定参考指令的高精度快速跟踪.首先是基于全状态反馈的干扰观测器－控制器分析设计，在仿真中可以看出，基于全状态反馈的干扰观测器－控制器对干扰有较好的响应，可以在遇到干扰时快速跟踪上期望值并保持稳定.而在基于输出反馈的干扰观测器－控制器设计分析与全状态反馈情况下类似，不同点在于基于全状态反馈的干扰观测器－控制器对于飞行器再入阶段，飞行器的角速率是未知的，只能通过观测器观测出来，进而进行误差的处理.

图4 飞行器角速率在时间变化下的曲线

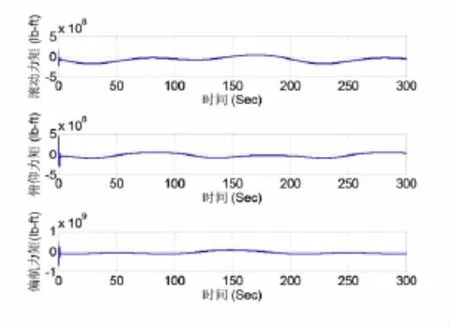
图5 飞行器控制力矩随时间变化曲线

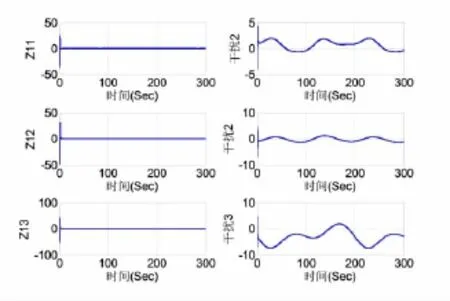
图6 飞行器再入阶段所受干扰随时间变化曲线

［1］Tian Bailing，Yin Liping，Wang Hong.Finite Time Reentry Attitude Control Based on Adaptive Multivariable Disturbance Compensation［J］.IEEE Transaction on Industrial Electronics，2015，62（9）：5889－5898.

［2］Tian Bailing，Fan Wenru，Qun Zong.Real－Time Trajectory and Attitude Coordination Control for Reusable Launch Vehicle in Reentry Phase［J］.IEEE Transaction on Industrial Electronics，2015，62（3）：1639－1650.

［3］Tian Bailing，Fan Wenru，Qun Zong.Integrated Guidance and Control for Reusable Launch Vehicle in Reentry Phase［J］.Nonlinear Dynamics，2015，80（1－2）：397－412.

［4］贾杰，荆泉.飞行器再入姿态双环滑模控制及其逻辑选择［J］.航天控制，2006，24（3）：25－28.

［5］N.X.Vinh，A.Busemann，R.D.Culp.Hypersonic and planetary entry flight mechanics［D］.Ann Arbor：University of Michigan Press，1980.

［6］N.X.Vinh，A.Busemann，R.D.Culp.Hypersonic and planetary entry flight mechanics［D］.Ann Arbor：University of Michigan Press，1980.

［7］M.V.Cook.Flight dynamics principles［M］.San Francisco：John Wiley ＆Sons Inc，1997.

Reentry attitude control based on adaptive multivariable disturbance compensation

HOU Ruizhe
（School of Software Engneering，South China University of Technology，GuangZhou 510641）

Research on control strategy based on multivariate disturbance observer－controller integrated reentry attitude in the framework of the full state feedback and output feedback respectively，which can track and research on high accuracy for custom guided instructions quickly under the comprehensive impact of uncertainty and external interference.Finally，perform simulation validation in Matlab／Simulink and analyze its stability.In the simulation we can see that，based on disturbance observer－output feedback controller has better response to interference，it can be encountered in the fast track the expectations and keep stable.

reentry aircraft；disturbance observer–controller；full state feedback and output feedback

V448 22＋2

A

1671-9476（2017）02-0059-07

10.13450／j.cnkij.zknu.2017.02.014

2016-11-10；

2017-01-25

侯睿哲（1996－），男，河南郸城人，硕士研究生，主要研究方向为软件编程与开发.