关于X0-sn-网的一些性质
2017-08-07刘士琴
刘士琴
(衡水学院 数学与计算机科学系 河北 衡水 053000)
关于X0-sn-网的一些性质
刘士琴
(衡水学院 数学与计算机科学系 河北 衡水 053000)
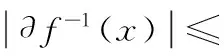
X0-sn-网; X0-sn-弱第一可数;cs-网; 弱基
0 引言
广义度量空间在一般拓扑学中占有极其重要的地位,众多学者从事该领域的研究工作并得到了较好的结果[1-7]. 文献[1]提出了X0-弱基的概念并对该概念进行了深入的研究,证明了当且仅当X具有点可数X0-弱基时,X是度量空间的商可数对一映射下的象.作为X0-弱基的概念的推广,文献[4]证明了当且仅当X具有点可数X0-sn-网时,X0-sn-网不是X0-弱基,它比X0-弱基还要弱,在该文中得到X是度量空间的序列商,可数对一映射下的象,通过特殊映射得到了关于X0-sn-网与可分度量空间的一些关系.本文通过特殊映射得到关于X0-sn-网的一些新的结果,所述空间均为正则T1的,所有映射均为连续的,N表示自然数,序列{xn:n∈N}、{pn:n∈N}分别为序列{Xn}、{Pn}的子序列.
1 预备知识
定义1[4]空间X的子集族B称为X的X0-sn-网,如果B=U{Bx(n):x∈X,n∈N},并且满足:1) 对每个x∈X,n∈N,Bx(n)是x的一个网,并且它在有限交下是封闭的,且x∈Bx(n).2) 空间X中L是收敛到x的一个序列,且x∉L,则存在L的一个子序列L′和n0∈N,使得对任意Bx(n0)∈Bx(n0),L′终于Bx(n0).
对于文献[1]中Sirois-Dumais定义,X称为X0-sn-弱第一可数,如果X有一个X0-sn-网,B=U{Bx(n):x∈X,n∈N},且对任意x∈X,n∈N,Bx(n)是可数的.
如果X具有一个σ-局部有限X0-sn-网,空间X称为X0-sn-度量空间.
文献[5]中定义的sn-网,如果对任意n∈N,Bx(n)=Bx(1),则B称为X中的sn-网.文献[6]中的定义,对任意x∈X,如果Bx(n)是可数的,则X称为sn-第一可数的.
定义2[1]设f:X→Y,f称为s-映射(紧映射,σ-紧映射),如果对任意y∈Y,f-1(y)是在X中的可分子集(紧子集,σ-紧子集).f称为边缘紧映射(边缘可数映射,边缘σ-紧映射),如果对任意y∈Y,∂f-1(y)是X中的紧子集(可数紧子集,σ-紧子集).
引理1[5]P是空间X中具有σ-遗传闭包保持子集.若P是X中的cs*-网,则P是X中的k-网.
2 主要结果
定理1X是X0-sn-弱第一可数空间,P是X中的一个点可数的cs-网,如果P是有限交封闭的,则P中存在一个子族B,使得B是X的一个X0-sn-网.
证明X是一个X0-sn-弱第一可数空间,令U{Bx(n):x∈X,n∈N}是X的一个X0-sn-网,Bx(n)={Bx(n,m):m∈N},且对每个m∈N,Bx(n,m+1)⊂Bx(n,m).P是X中的一个点可数cs-网,对任意n∈N,令Px(n)={P∈P:Bx(n,m)⊂P,∃m∈N},则Px(n)是有限交封闭的.B=U{Px(n):x∈X,n∈N},则B是P的一个子集族,只需证明B是X中的一个X0-sn-网.下面给出充分性的证明.
1) 对任意x∈X,n∈N,Px(n)是x的一个网.
若Px(n)不是x的一个网,则X中存在n∈N和x的一个邻域U,使得对任意P∈Px(n),都有P⊄U.令P∈P:x∈P⊂U={Pk:k∈N},则对任意的m,k∈NB(n,m)⊄U,对每个m≥k,取xmk∈B(n,m)Pk,令yi=xmk,其中i=k+m(m-1)/2,则在X中序列{yi}收敛于x,因为{Bx(n,m):m∈N}是X中x的递减网,既然P是X中的一个cs-网,则存在k,j∈N使得{yi:i≥j}⊂Pk,取i≥j,使得对某些m≥k,yi=xmk,则xmk∈Pk矛盾.
2)B是一个X0-sn-网.
假设序列L在X中收敛于x∉L,则X中存在L的一个子序列L′和n0∈N,使得对任意m∈N,L′终于Bx(n0,m).但是对某些m∈N,Bx(n0,m)⊂Px(n0),对任何Px(n0)∈Px(n),L′终于Px(n0).所以B是X中一个X0-sn-网.
定理2 设X是拓扑空间,则下述等价:
1)X具有点可数X0-sn-网.
2) 存在一个度量空间M和一个序列商点可数映射f:M→X.
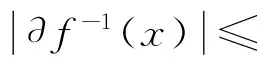
证明 由文献[4]知1)⟺2),且2)⟺3)显然.
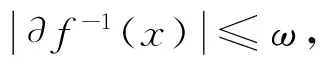
定理3X是一个fre′chet空间,则可数空间X是一个X0-sn-弱第一可数空间,当且仅当它是可数度量空间的可遗传的序列商映射下的象.
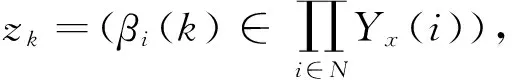
假设X是可数度量空间M的可遗传的序列商映射的象.f:M→Y是序列商映射.f-1(x)={xi:i∈N},只需要证明X对于x是X0-sn-弱第一可数的,令{C(n,m):m∈N}是M中xn的邻域,且是M的可数基B(n,m)=f(C(n,m)).则{B(n,m):m∈N}是可数的,对任意n∈N,令Bx(n)={B(n,m):m∈N},Bx(n)是可数的.从定义得到B=U{Bx(n):x∈X,n∈N}是X0-sn-网.
定理4 对于fre′chet空间X,下列是等价的:
1)X是X0-sn-度量空间.
2) 存在一个度量空间M和一个序列商σ可数对一映射f:M→X.
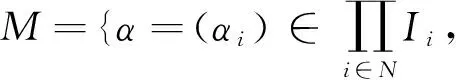
定义f:M→X使得f(αi)=x(α),在X中对任何n∈N,Bx(n)是Bx的一个网.容易得到f定义是合理且是到上的. 可得到M是度量空间,且f是连续的.注意到Pi是局部有限的,则f是可数对一的映射.对每个i∈N,αi∈Ii,令D(α1,α2,…,αn)={β=(βi)∈M:βi=αi,i≤n},且D={D(α1,α2,…,αn):αi∈βi,i≤n,n∈N},显然D是M的一个基,并且f(D(α1,α2,…,αn))=nBα.
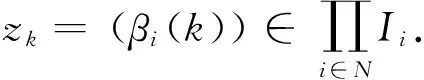
2)⟹1),由定理3得X是X0-sn-弱第一可数的.由于度量空间的商σ-的象是N空间,则X是X0-sn-度量空间.
[1] 林寿.广义度量空间与映射(第二版)[M].北京:科学出版社,2007.
[2] 林寿.点可数覆盖与序列覆盖映射[M].北京:科学出版社,2001.
[3] 李小龙, 张骞. 有序Banach空间非线性Neumann边值问题正解的存在性[J].郑州大学学报(理学版),2016,48(1):23-26.
[4] WANG P. On X0-sn-metricspaces[J]. 广西科学,2010,1: 32-35.
[5]GEY.sn-metric space[J].Acta Math Sinica,2002,45: 355-360.
[6] LIN S, YAN P. Sequence-covering maps of metric spaces[J].Topology and its applications,2001,109(3):301-314.
[7] 薛占熬,袁艺林,辛现伟,等. 多粒度广义L-模糊可变精度粗糙集[J]. 郑州大学学报(理学版),2016,48(3):82-89.
(责任编辑:方惠敏)
Some Properties on X0-sn-networks
LIU Shiqin
(DepartmentofMathematicsandComputer,HengshuiCollege,Hengshui053000,China)
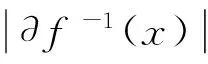
X0-sn-network; X0-sn-weakly first-countable;cs-network; weak bases
2017-02-21
国家自然科学基金资助项目(11301159);广西高校重点实验室项目(2016CSOBDP0004).
刘士琴(1982—)女,河北省衡水市人,讲师,主要从事一般拓扑学研究,E-mail:liushiqin168@163.com.
O
A
1671-6841(2017)03-0005-04
10.13705/j.issn.1671-6841.2017029
