货到人作业模式下的鱼骨型布局货位优化
2017-08-07宁方华何超群李英德
宁方华,何超群,李英德
(1.浙江理工大学机械与自动控制学院,杭州 310018;2.浙江工业大学机械工程学院,杭州 310014)
货到人作业模式下的鱼骨型布局货位优化
宁方华1,何超群1,李英德2
(1.浙江理工大学机械与自动控制学院,杭州 310018;2.浙江工业大学机械工程学院,杭州 310014)
为提高拣选效率,针对货到人模式的拣选特点,在鱼骨型布局中提出了基于品项相关性和货架相关性的货位优化方法。首先根据品项的相关性和订购频次划分品项簇,建立以最小化拣选路程为目标的货位分配模型,然后设计基于货架相关性的禁忌搜索算法(TS_SC)求解模型。该算法根据订单体积指数方法(COI)生成初始解,应用交换方式将相关性强的货架就近存储,缩短拣选路程。实验结果表明:相较于禁忌搜索算法,该算法收敛速度快,寻优能力强;相较于COI方法,该算法可有效减少货架搬运次数26.3%~39.6%,缩短拣选路程34.2%~48.6%。因此充分利用品项相关性和货架相关性进行货位优化,有利于提高货到人模式下的拣选效率。
鱼骨型布局;货到人;货位优化;相关性
随着物流自动化的推进,货到人拣选模式逐渐受到物流配送中心的重视。在物流配送中心的各项作业中,订单拣选时间占配送中心总作业时间的40%以上,拣选成本占总运营成本的65%以上,订单拣选消耗了配送中心的主要劳动力,是作业过程中最重要的流程[1]。因此高效的拣选作业可以提高配送中心的拣选效率,而货位优化是提高拣选效率的有效方法[2]。在基于移动式货架的货到人拣选模式中,货架处于运动状态,拣选人员固定在拣选台旁,AGV小车根据系统指令到达指定货架下,举起货架,将货架搬至指定拣选台前。由于拣选过程中AGV小车代替人工进行作业,极大地提高了物流拣选效率[3]。
货位优化研究中应用基于周转率和相关性的分配原则较多。其中基于周转率的货位分配研究起步较早,如Peterse等[4]提出了以品项所需仓储空间和被订购频次的比值为货位分配原则,Bernhard等[5]提出了ABC分类存储原则,该分配原则在需求不相关的情况下优化显著。考虑相关性的货位优化方法是将相关性强的品项指派到相近的货位中,如Mamzini[6]提出了在人至物拣货模式中获取相关性关系的3个启发式规则,李英德等[7]针对穿越策略下分区分批拣货时品项间相关性关系,提出了货位指派优化方法。
考虑品项相关性、订购频次的分配原则也适用于货到人作业模式,如:李珍萍等[8]根据订单中两种图书出现的次数,定义了两种图书之间的相关性,并以最大化同一货架上图书之间的平均关联度为目标建立了数学模型;周方圆等[9]根据货品的订购频次对物品进行聚类分组,并以总拣选成本最小化为目标确定了每个货架摆放的物品。应用品项相关性和订购频次对货位进行优化,降低了拣选成本、提高了拣选效率。但在货到人作业模式中,货架可移动且AGV小车可以在货架下行走,因此货位优化时不仅要将相关性强订购频次高的品项存储于一个货架中,减少货架搬运次数,还应将相关性强的货架就近摆放,减少AGV小车的行走路程。
本文研究货到人作业模式下的货位优化问题。首先根据订单信息,按品项的订购频次和相关性划分品项簇,将相关性强且订购频次高的品项簇存储于一个货架,并以最小化拣选路程为目标建立数学模型;然后设计TS_SC算法求解货位优化模型,将相关性强的货架就近存放,从而减少货架搬运次数,缩短拣选路程,提高作业效率。
一、问题描述与模型构建
(一)货位优化问题描述
传统的仓库布局一般由平行拣选巷道和与之垂直的横向通道构成,但Pohl等[10]、Roodbergen等[11]研究指出:横向通道不仅减少了货物的存储面积,尤其当一人拣选多位时增加了拣选货物的路程。针对传统布局方法的不足,Gue等[12]提出了鱼骨型仓储布局(如图1所示),鱼骨型布局由对角方向的中间通道、上方的垂直拣选巷道(区域2)、下方的水平拣选巷道(区域1、3)组成。该布局方法与传统的仓储布局相比,可减少20%左右的拣选路程,因此本文中的货架采用鱼骨型布局进行摆放。

图1 鱼骨型布局的货到人拣选模式注:← →表示AGV小车往返于货架与拣选台。
在鱼骨型布局中,采用基于可移动式货架的货到人拣选模式。拣选过程中,AGV小车根据控制系统的指令到达待拣选品项所在的货架下,举起货架搬运至指定的拣选台,拣选人员根据订单信息依次完成拣选任务,拣选完成后AGV小车根据指令移动至下一个拣选台或将货架搬回原始位置,从而开始下一个拣选任务,而空载的AGV小车可在货架下行走。对于单行订单,拣选人员直接将品项推至复核包装环节,而多行订单拣选人员需将品项先放入周转箱中,待订单拣选完成后再将周转箱转至复核包装环节。
(二)货位优化模型
针对货到人作业模式的特点,货位优化的目标有:a)最大化货架内品项的相关性,减少货架的搬运次数,其中两个品项同时出现在一个订单中,那么这两个品项相关,出现的次数越多,相关性越强;b)最大化货架间的相关性,减少AGV在货架间的行走路程,其中一个订单需拣选两个货架,那么这两个货架相关,两组货架共同完成的订单数量越多,相关性越强。
根据以上目标,分两步对品项进行货位优化:
a)根据订单信息将品项相关性强且订购频次高的品项划分为一簇,建立以拣选路程最小化为目标的数学模型;
b)根据货架相关性,设计求解货位优化模型的TS_SC算法,将相关性强的货架就近存放。
本文采用刘华婷等[13]提出的Apriori_LB算法对品项进行聚类。针对货到人作业模式的特点,应用该算法时将最后的频繁集降序排列后以货架的存储位数为阈值进行分组,使相关性强、订购频次高的品项尽量分配在一个货架中。
在聚类基础上,建立数学模型。模型假设:a)AGV小车从点st出发并最终回到st点;b)AGV小车按逆时针方向到各个拣选台进行拣选作业;c)每个储位上存放的物品数量足够每次拣选作业;d)每个货架只能存储一个品项簇;e)每个品项簇只能被指派到一个货架;f)拣选时AGV选择最近的货架进行搬运。
引入以下参数与变量:I为品项总数,品项编号为i=1,2,3,…,I;J为品项簇总数,品项簇编号为j=1,2,3,…,J;M为拣选通道总数,拣选通道编号为m=1,2,3,…,M;N为货架编号总数,货架编号为n=±1,±2,±3,…,±N;Q为拣选台总数,拣选台编号为q=1,2,3,…,Q;S为U型线的路程;f为拣选区域的长度;p为拣选区域,编号p=1,2,3;b为货架的长度;w为对角通道在水平和垂直方向的宽度;dv为垂直通道在对角通道方向的距离,dh为水平通道在对角通道方向的距离;α为对角通道倾斜的角度;Fj,j+1表示AGV小车拣选完品项簇j后去往下一个品项簇的路程;Hn:如果货架n为AGV小车第一个或最后一个搬运对象,其值为3,否则为2;Gnq,如果货架n访问了拣选台q,其值为1,否则为0。
决策变量xjpmn:如果品项簇j被指派到第p个拣选区域第m个拣选通道的第n个货架,其值为1,否则为0。
由图1中AGV小车拣选A、B、C三个货架的路线可知,AGV小车的行走路程分为三部分:往返于货架与拣选台的路程(虚线所示)、往返于拣选台间的路程(实线所示)、去往下一个货架的路程(点线所示)。

(1)
目标函数:
(2)
约束条件:

(3)

(4)

(5)
xjpmn,Gnq∈(0,1)
(6)
Hn∈(3,2)
(7)
模型中,式(2)表示以最小化拣选路程D为目标;式(3)表示每个货架只能存放一个品项簇;式(4)表示一个品项簇只能存放在一个货架上;式(5)表示一个订单至少需要搬运一个货架;式(6)和式(7)表示相关变量的取值范围。
二、货位优化方法
将品项簇指派到合适的位置上,相当于装箱问题,可应用禁忌搜索算法进行求解。算法采用禁忌策略回避搜索过程陷入局部最优的状况,应用特赦准则释放一些优良的禁忌对象,提高了搜索效率和解质量[14-15]。因此本文在禁忌搜索算法(tabu search,TS)的基础上,提出了基于货架相关性的禁忌搜索算法(tabu search considering shelf correlation,TS_SC)。该算法根据货架相关性设计邻域结构,应用交换货架位置的策略将相关性强的货架指派到相近且距离拣选台近的位置来提高拣选效率。
该算法的具体步骤如下:
第1步:设定最大迭代次数T、候选解集数量β、禁忌长度值η等参数,应用COI(cube-per-order index)方法产生初始解C0,令当前解C=C0,置空禁忌表。
初始解:统计每类品项簇的订购频次,根据订购频次进行储位指派,其中订购频次高的品项簇存放在距离拣选台近的货架上,同一通道内订购频次高的品项簇存储于距离通道入口近的货架上。
禁忌表:存放禁忌对象的容器,放入禁忌表中的禁忌对象只有被解禁后才能被再次搜索。
第2步:判断是否达到最大迭代次数要求t=T,如果达到,则算法结束,输出结果;否则,转至下一步。
第3步:根据当前解C的邻域结构生成邻域解,并从中确定β个候选解C′。
邻域结构:在当前解的基础上,应用移动策略产生一定数目的新解。TS算法的邻域结构为品项簇随机排序生成的表格,随机生成两个品项簇编号,交换编号对应的品项簇,多次进行该步骤产生邻域解。TS_SC算法采用基于货架相关性的邻域结构,即根据订单信息,统计任意两个品项簇的相关性强度,删除重复数据,将剩余的数据排列,在算法搜索过程中以随机方式选择其中一对品项簇,进行位置交换。
第4步:判断候选解是否满足特赦准则。将满足DC-DC,<0的最佳状态C′替换C成为新的当前解,并将C′对应的禁忌对象替换最早进入禁忌表的禁忌对象,同时用C′替换“best so far”的状态,得到当前最优解C*=C′,令C=C*,然后转至第6步;否则,转第5步。
禁忌对象:加入禁忌表的禁忌对象需设置禁忌长度值,搜索中每迭代一次,各禁忌对象的禁忌长度值自动减1,当禁忌长度值为0时,则删除该禁忌对象。
第5步:判断候选解C′对应各对象的禁忌情况,选择候选解集中非禁忌对象对应的最佳状态成为新的当前最优解C*=C′,令C=C*,并用与之对应的禁忌对象替换最早进入禁忌表的禁忌对象。
第6步:t=t+1,转第2步。
三、算法测试与分析
为分析考虑相关性对拣选效率的影响以及算法的效果,设计如下实验:随机生成一组订单,对比TS算法,分析验证TS_SC算法的优越性;随机生成多组不同数量的订单和货架储位组合数据,对比COI方法分析相关性对拣选效率的影响。
在VS 2010环境下实现COI方法、TS算法、TS_SC算法求解货位优化问题的测试程序。在WIN8 64Bit操作系统、8GB内存和Intel(R) Core(TM) i5-4200(2.29GHz)环境下进行实验,基本参数设置如表1所示。
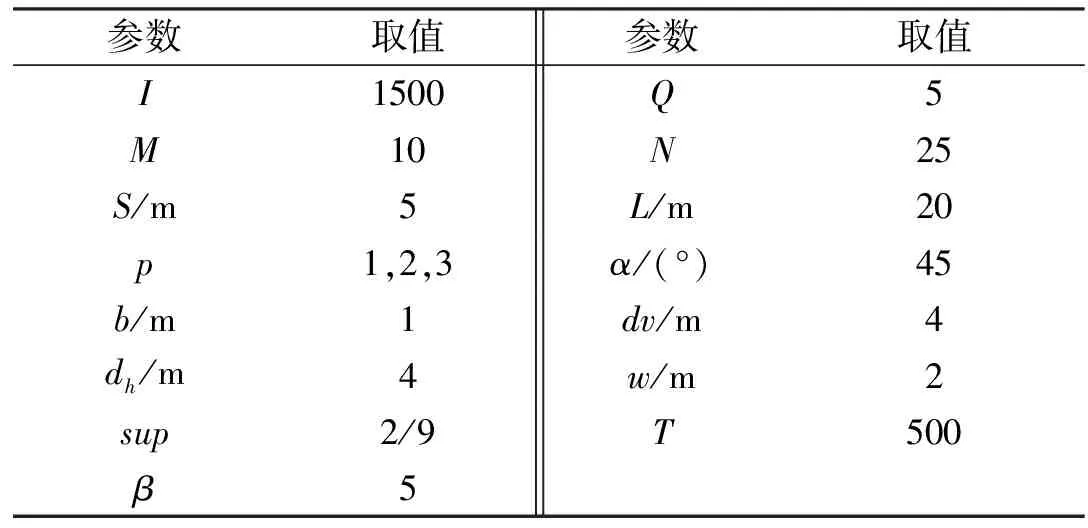
表1 基本参数
(一)算法性能测试
随机生成250张订单,每张订单随机包含1~15个订单行,货架存储货位数为8。利用表1数据对TS算法和TS_SC算法进行收敛性、运行速度测试结果如图2所示。可以看出:
a)收敛性:两种算法都能收敛于某点。TS_SC算法约迭代至320代达到平衡,相对于TS算法迭代450代达到平衡,收敛速度得到了改善,可见基于相关性的货位搜索策略提高了算法的收敛速度,缩短了检索时间。
b)寻优能力:TS_SC算法的寻优能力要好于TS算法。TS_SC算法得到的总拣选距离是2.75 km,相对于TS算法解2.94 km缩短了6.9%。TS_SC算法采用基于相关性的品项簇交换策略进行移动搜索,提高了搜索效率;同时使较差个体得到改善,增强了算法的寻优能力。

图2 两种算法基本性能测试结果
(二)拣选效率
为检验TS_SC算法的优越性,设计不同订单数量f=600、800、1000,货架存储位数nog=8、12、16的实验组合,对比根据订货频次对品项进行聚类划分,按照品项簇订购频次的高低决定存放距离拣选台远近货架的COI方法,实验运行不同订单数量和存储位数排列组合后的拣选过程,取货架搬运次数、最优解的平均值。其中LCOI、LTS_SC分别表示COI、TS_SC算法的货架搬运次数,DCOI、DTS_SC表示COI、TS_SC方法求解出货位优化后的总拣选路程。
1.货架搬运次数
a)订单数量与货架搬运次数实验结果曲线见图3,由图3可知,当货架存储货位的数量一定时,货架搬运次数(LCOI、LTS_SC)随着订单数量的增长而趋于平缓;说明订单数量越多,品项相关性越明显,货架搬运次数相对减少。

图3 订单数量与搬运次数
b)货架存储位数与搬运次数实验结果曲线见图4,由图4可知,当订单数量一定时,货架搬运次数(LCOI、LTS_SC)随着货架存储位数量的增大而减少;说明货架储位越多,货架相关性越强,货架搬运次数越少。

图4 货架存储位数与搬运次数
c)COI、TS_SC方法求解的货架搬运次数结果见图5,由图5可知,在不同存储位数、订单数量的组合情况下,相较于COI方法,TS_SC方法减少了26.3%~39.6%的货架搬运次数。

图5 两种算法求解的货架搬运次数注:三组数据的订单数量依次是600、800、1000张。
2.拣选路程
由图6(a)拣选次数与拣选距离可知,在相同订单数和货架储位数时,TS_SC方法的拣选路程(DTS_SC)普遍低于COI方法求解的拣选路程(DCOI)。由图6(b)优化结果看出,相较于COI方法,TS_SC算法缩短了34.2%~48.6%的拣选路程。由此说明,TS_SC方法对提高拣选效率有显著效果。

图6 两种算法求解的拣选路程注:三组数据的订单数量依次是600、800、1000张。
四、结 论
本文研究了货到人作业模式下鱼骨型布局中的货位优化问题,根据品项的订购频次和相关性进行聚类,建立了以最小化拣选路程为目标的数学模型,提出了TS_SC算法,并随机生成一批订单,对算法性能和效果进行实验。结果表明:a)相较于TS算法,TS_SC算法具有较快的收敛速度,较优的寻优能力;b)随着订单的增长,品项相关性越明显;c)随着货架存储数量的增多,货架相关性增强,货架的搬运次数减少,订单完成率提高;d)相较于COI方法,TS_SC方法减少了货架搬运次数,缩短了搬运路程,提高了拣选效率。
后续研究将考虑以最少的货架和最优的货位分配来提高拣选效率,进一步降低成本。
[1] 吴颖颖,孟祥旭,王艳艳,等.“货到人”拣选系统订单排序优化[J].机械工程学报,2016,52(4):206-212.
[2] KOSTER R D, DUC T L,ROODBERGEN K J. Design and control of warehouse order picking: A literature review[J].European Journal of Operation Reserch,2007,182(2):481-501.
[3] 邹爽心.仓储机器人的应用现状与发展战略探讨[J].物流工程与管理,2013,35(6):171-172.
[4] PETERSE C G, AASE G R, HEISER D R. Improving order picking performance through the implementation of class-based storage[J].International Journal of Physical and Logistical Management,2004,34(7):534-544.
[5] BERMHARD F, ANDREAS K. Distribution Logistics: Advanced Solutions to Practical Problems [M].Berlin: Springer,2005:185-200.
[6] MAMZINI R. Correlated storage assignment in an order picking system[J]. International Journal of Industrial Engineering,2006,13(4):1675-1692.
[7] 李英德,鲁建厦,潘国强.穿越策略下考虑相关性的货位优化方法[J].浙江大学学报(工学版),2012,46(8):1424-1430.
[8] 李珍萍,李文玉.网上书店智能仓库系统储位优化研究[J].物流技术,2014,23:340-342.
[9] 周方圆,李珍萍.基于“货到人”拣选模式的储位分配模型与算法[J].物流技术,2015,34(9):242-246.
[10] POHL L M, MELLER R D, GUE K R. An analysis of dual-command operations in common warehouse designs[J]. Transportation Research Part E Logistics & Transportation Review,2009,45(3):367-379.
[11] ROODBERGEN K J, KOSTER R D. Routing order pickers in a warehouse with a middle aisle[J]. European Journal of Operational Research,2001,133(1):32-43.
[12] GUE R K, MELLER D R. Aisle configurations for unit-load warehouses[J]. IIE Transactions,2009,41(3):171-182.
[13] 刘华婷,郭仁祥,姜浩.关联规则挖掘Apriori算法的研究与改进[J].计算机应用与软件,2009,26(1):146-149.
[14] 王凌.智能优化算法及其应用[M].北京:清华大学出版社,2001:62-82.
[15] 董宗然,周慧.禁忌搜索算法评述[J].软件工程师,2010(s1):96-98.
(责任编辑: 康 锋)
Study on Slotting Optimization of Fishbone Layout Based on Rack-to-Picker Mode
NINGFanghua1,HEChaoqun1,LIYingde2
(1.Faculty of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China; 2.College of Mechanical Engineering,Zhejiang University of Technology, Hangzhou 310014, China)
In order to improve the picking efficiency of the rack-to-picker picking mode, this paper puts forward slotting optimization method based on SKUs correlation and shelf correlation in the fishbone layout. Firstly, the SKU clusters were divided according to the SKUs correlation and the order frequency, and slotting allocation mode with the goal of minimizing picking route was established. Then, tabu search algorithm based on shelf correlation (TS-SC) was designed to solve the mathematical model. The algorithm generates the initial solution according to the COI solution and applies the way of exchange to store the shelves with strong correlation to shorten the picking route. The results show that compared with tabu search algorithm, this algorithm has faster rate of convergence and stronger optimization ability. Compared with COI method, this algorithm can effectively reduce the number of rack movements from 26.3% to 39.6% and shorten picking route from 34.2% to 48.6%. So, making the best of SKUs correlation and shelf correlation for slotting optimization contributes to improving picking efficiency under rack-to-picker mode.
fishbone layout; rack-to-picker; slotting optimization; correlation
10.3969/j.issn.1673-3851.2017.08.002
2016-11-22 网络出版日期:2017-03-28
宁方华(1978-),女,山东泰安人,副教授,主要从事物流与供应链管理、生产系统建模与仿真方面的研究。
TP399
A
1673- 3851 (2017) 04- 0293- 06
