企改中基于M ES的加工过程质量控制与预测研究

2017-08-07辛梅

经济研究导刊 2017年21期

关键词：粒子向量误差

辛梅

（西安航空职业技术学院航空制造工程学院，西安 710089）

企改中基于M ES的加工过程质量控制与预测研究

辛梅

（西安航空职业技术学院航空制造工程学院，西安 710089）

针对制造加工零部件生产高精度控制的需求，结合加工质量控制理论，提出一种基于人工智能算法的质量控制与预测系统。为提高质量控制精度，提出一种基于改进的SVR预测模型。借助SVR预测算法可处理非线性和高维度等复杂问题，以及粒子算法在全局搜索方面的优势，对SVR预测的参数进行优化。同时根据上述的算法，构建加工质量预测控制模型。最后，通过MatLab软件对上述算法进行验证，结果表明上述加工方法具有可行性。

加工质量；制造执行系统；预测；粒子群算法；支持向量机

随着现代加工过程的数字化发展，以及基于制造执行系统（MES）控制的信息化，产品批量化生产成为离散制造业发展的一种趋势，而加强质量控制成为核心。目前，针对制造企业加工过程质量控制，主要集中在人工智能控制和基于SPC工序质量控制两类。如魏青云（2012）提出借助神经网络算法、薛丽（2016）则提出通过抽样区间算法及EWMA控制图、牛占文（2010）提出通过的累积和控制图及指数加权移动平均指数等方法，都对零部件加工质量进行了控制。对此，基于MES系统和上述的研究成果，提出一种对批量化产品生产质量预测算法，并对算法的可行性进行验证。

一、支持向量回归原理

（一）不敏感损失函数

SVR回归算法中，将损失函数的定义为：

公式（1）表示，如估计器输出的结果y与期望值d之间的偏差的绝对值小于某个指定的参数ε，则其值等于0，否则等于偏差减去绝对值减去指定参数ε。

（二）基于ε不敏感损失函数的SVR

对SVR回归的描述：假设在n维空间当中，存在l个数据样本对{（xi，yi），i=1，2，…l}，其中，xi∈Rn表示第i个样本的输入向量，yi∈R表示为与相对应的输出值，由此在n维空间中存在超平面f（x）=wx+b，使得该平面与任意的一个样本点的距离最大。同时，考虑到在数据的采集中存在干扰的问题，引入松弛变量ξ和ξ*及误差惩罚因子C，其中ξ和ξ*分别代表数据点超出不敏感区的上限误差和下限误差，由此可以得到以下优化问题：

其中，C值越大，表示其对错分的惩罚也就越重，分类也就越严格。

为求解上述的方程，引入拉格朗日乘子法，引入乘子αi和βi，并根据KKT原则，可得到ε-SVR模型求解的对偶形式：

对公式（3）进行求解，可以得到最优分类面函数：

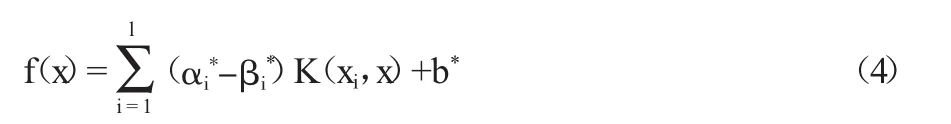
其中，αi*、βi*、b*分别表示二次规划函数最优解，K（xi，x）表示核函数。

核函数选择RBF核函数。

其中，σ表示高斯核宽度参数。

由此，通过上述公式的表达式可以看出，在SVR模型中，影响模型的分类性能的参数只有σ和C惩罚因子。因此，要保证模型得到最优解，只需要对参数σ和C进行优化即可。

二、基于PSO-SVR的质量控制与预测模型构建

要保证参数σ和C参数最优，就必须防止陷入局部最优。因此，引入PSO在全局搜索方面的优势，对参数σ和C两个参数进行优化，从而得到最优的参数。PSO算法的原理是借助个体之间的竞争、交流、合作和信息共享等机制来实现最优解。在求解最优的过程中，假设最优可行解在D维空间上面的点，即“粒子”要求解该粒子，首先会产生N={X1，X2，…，XN}个潜在解，在每个Xi中会产生xi1～xid个当前解。在迭代的过程中，每个粒子会之前的种群最优和个体最优信息不断的调整自身的位置。对此引入惯性权重和学习因子对其调整进行表示，具体表达式为：

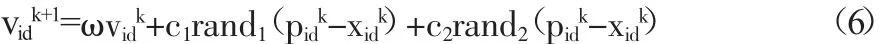
其中，c1和c2表示加速度因子，根据经验，c1=c2=1.5；ω表示惯性权重，该值越大越有利于全局搜素，越小越有利于局部搜索。

同时，为进一步对产品加工进行修正，引入误差补偿思想，即通过PSO-SVR模型求解得到加工工序的预测误差，然后将该预测误差与实际误差进行比较，如果在误差范围之内，那么统计下一个工件的误差，如果超过误差要求的范围，对误差进行补偿或者调整加工工艺，从而达到对批量产品质量调整的目标。由此，综上可以得到质量预测控制流程，具体（如下图所示）。

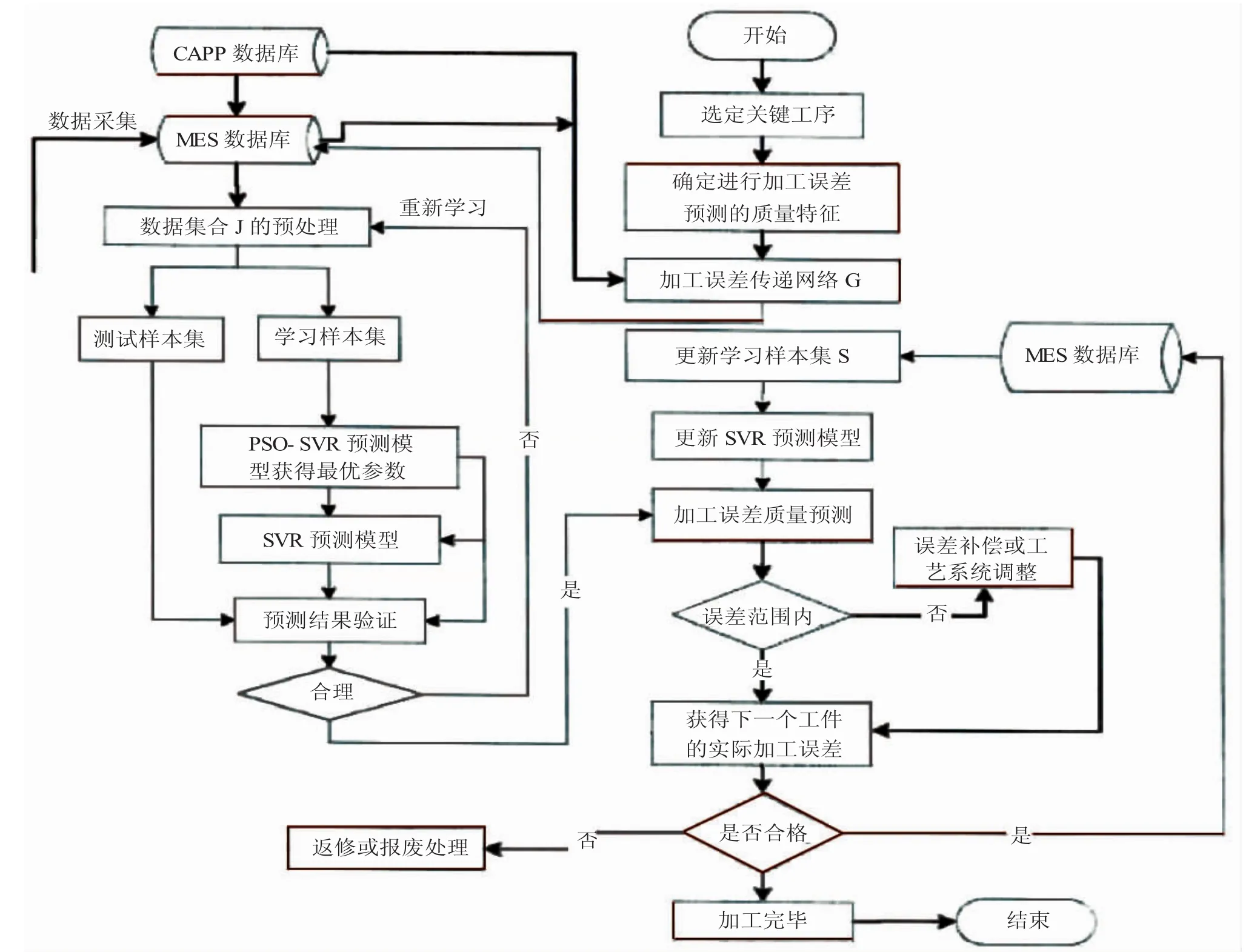
质量预测控制模型图

三、仿真验证

为验证上述上述优化算法的效果，利用Matlab软件进行仿真。设数据样本为20，其中学习样本15，测试样本5，c1=c2=1.5，最大迭代次数为200次，惯性权重采用二次曲线进行动态调整，C∈[1，1000]，σ∈[0.001,3.8]，ε∈[10-5，10-4]。通过上述的仿真，当适应度函数值最小时，可以得到当迭代次数为120次，得到最优粒子向量参数。同时，将上述的最优粒子向量代入到SVR模型中，得到预测值和实际测量值之间的误差在[-0.002，0.002]的水平，说明本文构建的质量预测控制模型有效，并且可满足短期误差控制需求。