基于ARIMA模型对上证指数趋势的预测

◎李晓先

基于ARIMA模型对上证指数趋势的预测

◎李晓先

股票市场的发展在一定程度上反应了一个国家或地区的经济水平，而指数则是反应股市运行状况的综合指标。其中，上证指数作为我国几大具有代表性的指数之一，在一定程度上综合反应了我国股市的发展趋势。再者，当今股票市场的波动时刻牵动着国内外亿万投资者的心弦，因此对上证指数趋势的研究具有强烈的现实意义。基于此，本文选取2005年1月4日至2016年12月16日的上证指数数据，运用ARIMA模型进行了预测。研究发现，在短期内ARIMA模型对上证指数的预测效果较好。

ARIMA模型 上证指数 自相关函数 偏相关函数

股票市场起源于17世纪的荷兰，发展至今，其作用和影响力巨大，可以说它是一个国家或地区经济和金融活动的晴雨表。很多时候股票市场的不稳定波动可能危害一国经济的健康发展。对于国家管理者而言，能够准确预测股票价格的走势，及时对股票市场进行合理的干预和健康的引导，将促使国家经济持续健康的发展，也可以使投资者的损失最小化、收益最大化，间接起到拉动投资的作用。对于投资者而言，股票市场的波动直接影响其股票收益，或是影响其对公司所有权部分的分红，就外国投资者而言可能还影响其对国内的投资额度。因此，对股票市场运行状况进行预测分析研究，明确股票市场的运行趋势有助于掌握一国地区的经济运行状况，并为当局管理国家金融事项提供帮助，也为投资者进行投资提供良好的建议并加强其信心。

一、预测模型

对时间序列进行预测的方法有很多，如一次指数平滑、二次指数平滑、门限自回归、灰色预测等。本文基于学者的成果经验，最终选择在金融领域预测效果较佳的ARIMA模型对上证指数进行预测。

ARIMA模型全称为自回归移动平均模型（Autoregressive Integrated Moving Average Model，简记ARIMA），实质上是自回归移动平均模型（ARMA）的扩展，是由Box和Jenkins于上世纪70年代初创立的著名时间序列预测方法，又称为“B-J模型”。其中，AR是自回归，p为自回归项；MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数。

ARIMA模型的基本思想是：将预测对象随时间推移而形成的数据序列视为一个随机序列，该随机序列的单个值虽然具有不确定性，但其整体而言却是具有一定的规律。因此，可以用一定的数学模型来近似描述这个序列，通过数学方法，使该序列达到最小方差下的最优预测。下面几项为与模型相关的内容。

（一）自相关函数（ACF）

自相关函数记为ρt,s=Corr（Yt，Ys），t，s=0，±1，±2……

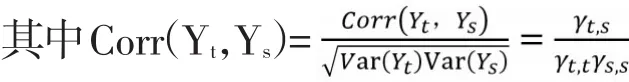
ρt,s表示同一个指标不同时间的两个变量之间的相关关系，越接近于±1，说明变量的自相关越强，若接近于0，说明两者之间几乎没有相关性，等于0就是不相关。

（二）偏相关函数（PACF）

ACF衡量的是Yt与Yt-k之间的相关性，并不考虑Yt与Yt-1，Yt-2，……Yt-k+1之间的关系，而PACF是考量当Yt-1，Yt-2，……Yt-k+1保持不变时，Yt-k与Yt之间的相关性，两者的不同之处在于对其他变量的控制不同。

PACF记如下表达式：

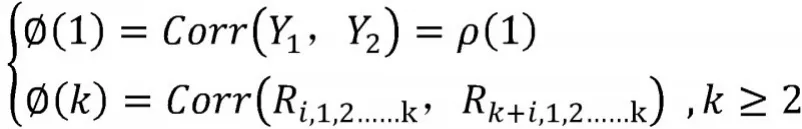
其中，Ri,1,2……,k是由Yi关于（Y2……Yk）的线性回归所得的残差。

（三）ARIMA模型

ARIMA的表达式可以写成三种形式。

第一种，AR（p）模型对应的表达式。

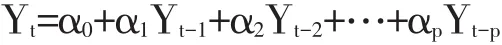
第二种，MA（q）模型的表达式。

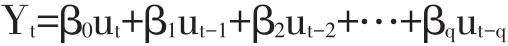
第三种，ARMA（p，q）模型的表达式。

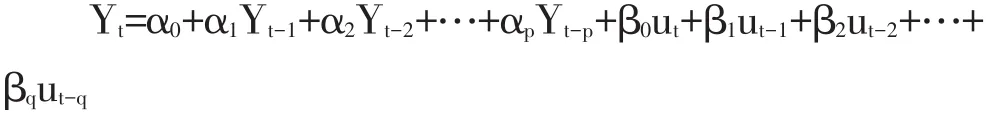
其实，第三种ARMA模型就是第一种与第二种的结合体，然后再考虑一个时间序列的滞后项问题，引入一个d参数，使时间序列达到平衡状态，就是最终的ARIMA模型。

二、数据来源与处理

（一）数据来源

本文所选数据来源于国泰君安数据库，截至2017年5月，数据库对上证指数更新到2016年12月16日。以12月份的数据作为对比数据，与模型预测结果进行对比，检验模型的预测效果。2016年12月以前的数据作为建立模型进行预测作用。

（二）模型步骤

ARIMA模型具体步骤如下所示。

步骤一：对原始数据进行预处理，主要包括选取适当长度的数据，以及对数据进行稳性检验，若不平稳，则进行差分处理成平稳的序列。

步骤二：检验ACF与PACF，确实ARIMA（p，d，q）各参数的值。

步骤三：进行模型估计，选出最优的模型。

步骤四：对建立后的模型进行白噪声检验，若通过则进行下一步。

步骤五：利用通过检验的ARIMA模型对未来走势进行预测。

三、实证分析

（一）时间序列的平稳性检验

由于时间序列数据一般来说都是不平稳的，因此在进行时间序列预测模型估计前，都要先对序列进行平稳性（ADF）检验，若不平稳则通过差分处理，转化为平稳的序列。当然，即使差分后转变成了平稳的序列，但转化的序列已经没有分析的价值，那么这序列也就不适合时间序列模型的预测估计，或是要通过别的方法对其数据进行优化处理。

图1中的Y图明显可以看出，此序列不平稳，于是采取平稳性检验，结果如下所示。

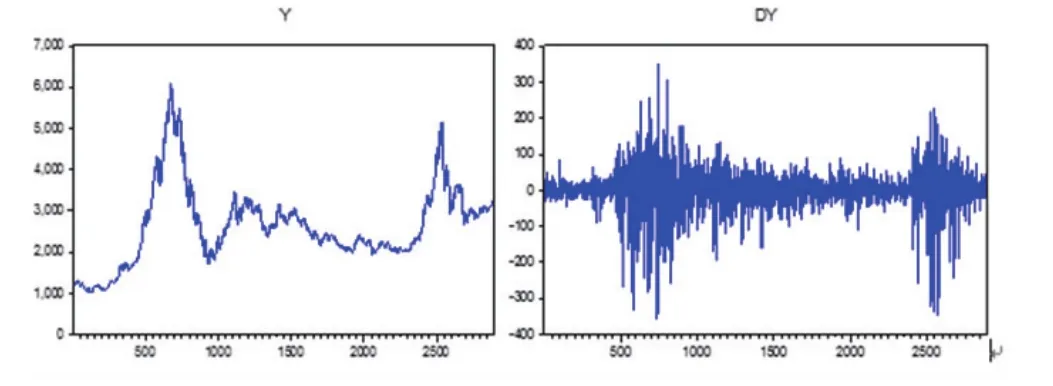
图1 序列原始图与一阶差分后的图

从表1中可以看出，原始数据经过一阶差分后达到平稳状态，也就确立模型中d的取值为1。

间接的从图1也可以看出，其中左边部分为原始序列形态，右边部分为一阶差分图，经过差分后总体达到平稳状态，然而在当期以及前期还有部分不平稳状态，但我们不考虑少部份异常值的影响。

表1 原始数据与一阶差分数据的平稳性检验结果

（二）ACF与PACF图检验

ACF与PACF主要是检验两变量间的自相关关系以及两变量间的偏相关关系，在此处的主要作用是用以确立ARIMA模型中p，q的值。

前面已经确定上证指数经过一阶差分处理后才平稳，现就对其一阶差分形式进行检验选择。

自相关的检验结果告诉我们，在滞后期为4时，序列的样本自相关系数才落入随机区间内。

偏相关的检验结果告诉我们，在滞后期为6时，序列的样本系数落入随机区间，但在滞后期为13时，再次偏离随机区间，表现拖尾，但最终还是选择滞后期为6时的结果。

综合上述ACF与PACF的检验结果，我们确立ARIMA模型中p、q的值分别为4与6，也就确立了我们最终所要的模型ARIMA（4，1，6）

（三）模型检验

最终估计出来的模型，能不能符合实际情况还不得而知，要经过一定的检验才能说明这个模型的估计是有效的，于是这里我们采取对估计模型的残差序列做白噪声检验（见图2）。

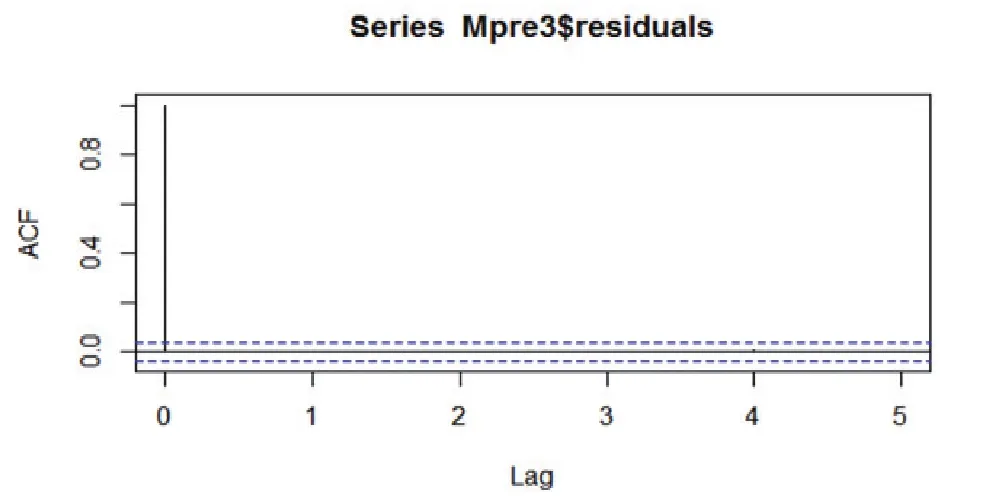
图2 白噪声检验

从图2中可以看出ARIMA（4，1，6）通过白噪声检验，适用于时间序列上证指数的建模与预测。

（四）上证指数的预测

上面已经验证模型可以用于上证指数的预测，我们先看一下预测结果图（本文实际预测了未来20个交易日的走势，但由于数据原因我们只对比12月16日前的数据）。

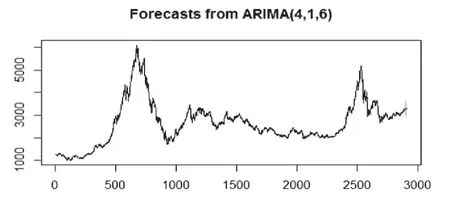
图3 上证指数未来20个交易日的预测情况

为了使图片上的预测效果看起来更加直观，另外选取最近100个交易日的数据进行预测（见图4）。

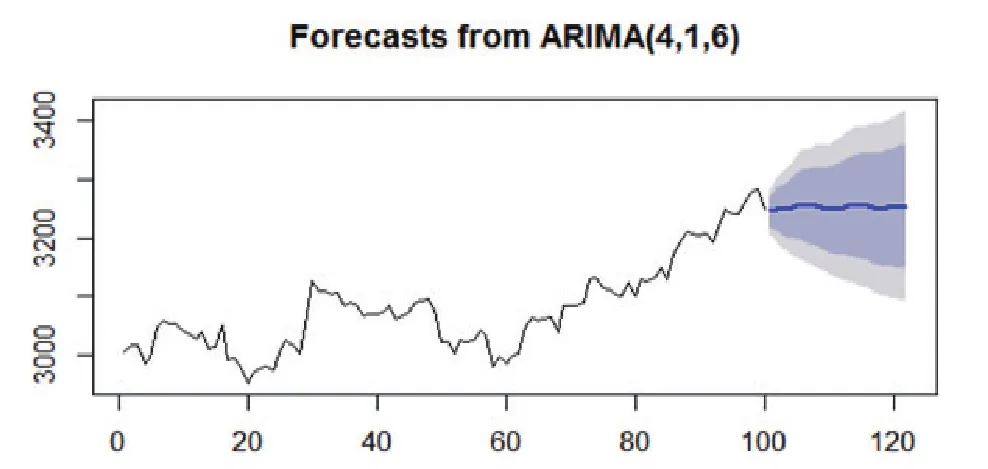
图4 基于ARIMA（4，1，6），以100个历史数据为基础的预测区域

图3、图4蓝色线条为预测线，蓝色周围的深灰色部分为80%的预测域，浅灰色的部分为95%的预测域。大致可以看出，未来预测值总的趋势表现为平稳状态。具体情况看基于2893个历史数据的ARIMA（4，1，6）预测值与实际值之间的对比（见表2）。

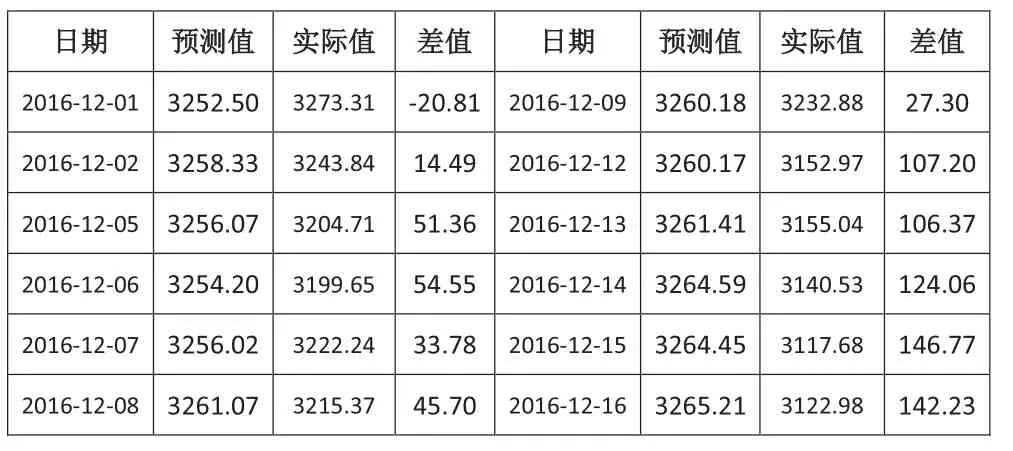
表2 未来一个月的预测值与真实值对比

表2中对预测值与实际值之间做了一个数值的对比，结果表明前七个交易日的预测效果较好，后面五个交易日的预测数据则差距比较大。

四、结论与建议

目前，用于预测时间序列趋势的方法相对来说较多，如前面提到的灰色预测、指数平滑、门限自回归等方法，每个方法都有一定的预测优势，但同样存在一定的不足之处，因为每一个方法的创立之初都是为了解决特定问题而产生的。本文所采用的ARIMA模型，在经济领域相对来说是效果较佳的一种预测方法。从最后的预测结果与实际发生值之间进行对比发现，在未来七个交易日的预测较好，之后则效果比较差，甚至与实际发生值偏离较大。因此，用该方法进行预测也要考虑相应的时效性。

另外，股票市场的实际波动比较大，受很多的影响因素干扰，有市场风险、政治风险、技术风险等。单纯仅靠一个模型去做预测是不够的，甚至有时候用同一指标的不同时间段的数据进行预测都会得出不同预测结果。因此，需要结合其他方法与经济事实进行综合判断。

（作者单位：江西财经大学统计学院）

责任编辑：宋 爽