频域抗窄带干扰在弹载卫星导航接收机中的应用

中国空空导弹研究院 李园地

频域抗窄带干扰在弹载卫星导航接收机中的应用

中国空空导弹研究院 李园地

频域抗窄带干扰技术实现简单，对快时变干扰迅速作出反应并且对干扰类型不敏感，非常适合弹载卫星导航接收机。本文主要分析了不同窗函数的特性和优化选择，根据加窗带来的信噪比损失分析了不同重叠处理的效果，提出了以海明窗作为窗函数，以重叠相加作为重叠处理的频域抗窄带干扰方案，最终通过仿真验证了效果。

卫星导航；抗窄带干扰；窗函数；重叠处理

1.引言

全球卫星导航系统（GNSS）的主要工作是为军事和民用提供定位、测速、授时、导航等业务，已经广泛应用于各种武器平台，成为精确制导武器中常用的制导手段。目前，我院在制导炸弹、远程空空导弹等长航时、远距离的型号中已开始应用卫星导航技术作为有效的辅助惯导手段。然而由于卫星信号到达地面的功率远低于接收机热噪声功率，因此特别容易受到各种各样的干扰。虽然卫星导航系统采用扩频通信本身通信本身具有一定程度的抗干扰能力，但面对高强度的人为干扰，必须借助抗干扰技术来提高系统的抗干扰能力。

现在使用的接收机多采用空域抗干扰方式，能够有效抑制宽带干扰和窄带干扰，但是干扰抑制个数受天线的阵元个数限制。在空空导弹上由于体积的限制，天线的数量受到严格控制，因此，可在空域抗干扰前先进行窄带抗干扰消除窄带干扰信号，将无法消除的宽带干扰交给空域抗干扰处理，提抗干扰能力。目前常用的抗窄带技术主要有时域和频域两种抗干扰技术。时域抗干扰技术、实现简单，但时域抗干扰算法需要长时间的迭代才能达到稳定状态，无法跟踪快变干扰，当干扰的个数增加或者能量改变时，干扰能力迅速下降。频域抗干扰技术相对于时域抗干扰技术频域抗干扰技术不需要收敛过程，能对快时变干扰迅速做出反应，且对干扰的模型不敏感，比较适合用于快时变窄带干扰抑制。因此，频域抗干扰技术的研究对弹载卫星导航接收机就具有重要的意义。

2.频域抗窄带干扰技术原理

卫星导航信号是扩频信号，其频谱在一个很宽的频带内十分平坦。而窄带干扰信号的能量则集中在少数频点上，呈现出高而窄的脉冲形状。频域窄带抑制技术的主要原理就是利用扩频信号和窄带干扰信号在频域中表现出极大差异的特性，通过FFT变换将输入的时域信号映射到对应特征的变换频谱空间中，由于这些频谱之间相对独立互不影响而且窄带干扰比较集中，所以通过合理的检测手段对含有窄带干扰的子频谱空间进行辨别并实施频谱幅度的衰减或者置零处理，最后再将进行抑制后的频域信号通过IFFT反变换恢复到时域，通过这一系列数字信号处理过程来消除窄带干扰。频域抗窄带干扰的原理框图如图1所示：

图1 频域抗窄带干扰的原理框图

3.窗函数的选择

由图1可以看出，频域抗窄带干扰首先要对输入信号进行FFT运算。在实际中，输入信号可以看做是无限长的，而用FFT进行频谱分析时每次处理的数据序列长度有限，所以要对数据序列进行截断，这样就隐含了对采样数据频域的周期拓展，不可避免地会造成频谱泄露效应。尤其是当存在强窄带干扰时，频率泄露效应会更加严重，使受干扰污染的谱线数大大增加，从而造成在对干扰谱线进行抑制时，对有用信号造成更多损失。为了减小频谱泄露效应，常用的做法是对信号进行加窗处理，即在时域将离散信号进行加权平滑处理，减少突然截断造成的频谱泄露效应，得到更好的频谱特性。

不同的窗函数对FFT变换的频谱泄露抑制程度不一样，这主要有主瓣宽度和旁瓣值来决定，不加窗的情况等效于加矩形窗，常见的窗函数有三角窗、汉宁窗、海明窗和布莱克曼窗。图2是通过MATLAB仿真的64点各窗函数的时域幅度图和频域幅度特性曲线。

图2 各窗函数的时域幅度图和频域幅度特性曲线

在处理窄带干扰时，们希望选择主瓣窄且旁瓣低的窗函数。通过仿真可以发现，矩形窗的第一旁瓣比主瓣仅仅低13.3dB，旁瓣太高导致频谱泄露严重；三角窗主瓣宽度是矩形窗的两倍，第一旁瓣比主瓣低25dB；汉宁窗的第一旁瓣比主瓣低31.5dB，主瓣宽度是矩形窗的两倍；海明窗的第一旁瓣比主瓣低42.7dB，主瓣宽度和汉宁窗一样；布莱克曼窗的第一旁瓣最低，比主瓣低58.1dB，但其主瓣宽度最宽，是汉宁窗和海明窗的两倍。综合考虑，海明窗函数在各方面表现比较均衡，因此常被使用。

4.重叠处理

加窗虽然改善了频谱泄露效应，但同时窗两端的衰减也对有用信号造成了失真，加窗对信号的影响可以用信噪比损失来评估。假设x(k)= s(k)+ n(k) )是接收信号，其中s(k)是导航信号，其幅度大小为A，n(k)是均值为0、方差为的高斯白噪声序列，窗函数为w(k),k=1,2,...,N,。则加窗带来的信噪比损失为：

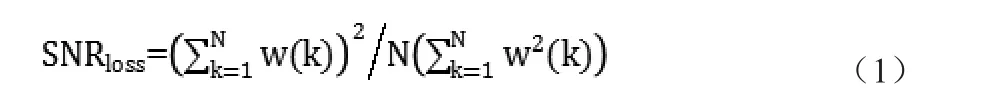
为了减轻加窗带来的信噪比损失，可采用重叠的方法。重叠因子r越大，加窗造成的信噪比损失就越小，但是处理的复杂度和计算开销就越大。在重叠因子的选择上，1/3重叠仍有较大信噪比损失，而1/2、2/3重叠基本已无损耗，并且1/2重叠的复杂度和计算量较小，因此1/2重叠是一种较为合理的选择。以1/2重叠为例，假设窗函数为w(k),k=1,2,...,N,首先将输入信号分为两路，一路直接进行加窗FFT，另一路先进行N/2延迟，然后再进行加窗FFT、干扰抑制、IFFT。经过处理后的两路数据在合成时，有两种方式：

（1）重叠选择即两路信号分别选择对应窗函数中扭曲较小部分输出。对于1/2重叠选择输出方式，加窗带来的信噪比损失为：

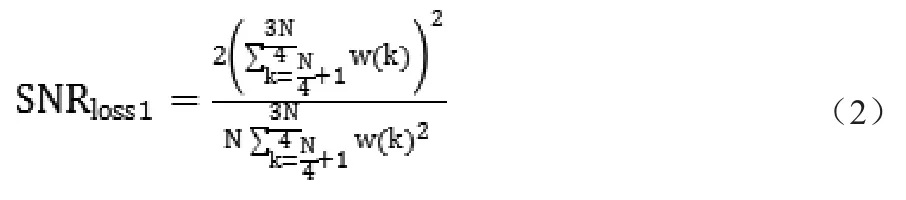
（2）重叠相加即两路信号重叠部分相加输出。对于1/2重叠相加输出方式，加窗带来的信噪比损失为：

根据公式2和3，表1给出了不同窗函数和重叠方式的信噪比损失。

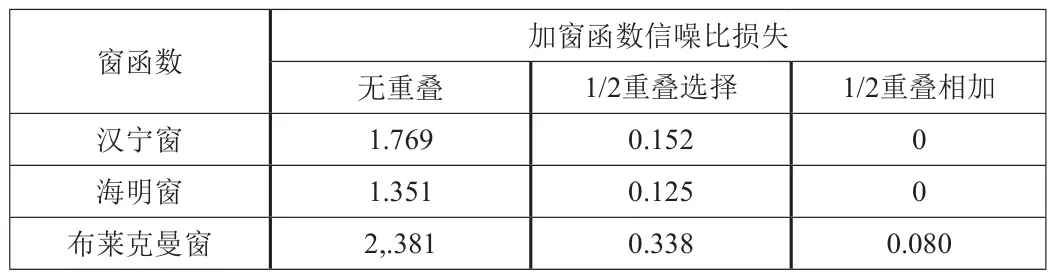
表1 不同窗函数和重叠方式的信噪比损失

通过表1明显看出，重叠能够明显改善加窗带来的信噪比损失。对于同样的窗函数和重叠比例而言，重叠相加一般都比重叠选择的损耗更小。对于汉宁窗和海明窗来说，1/2重叠相加能够做到准确重构原始信号，使加窗带来的信噪比损失可忽略不计。

5.仿真结果

仿真采用海明窗函数和1/2重叠相加处理，干扰抑制算法采用采用N-sigma算法，导航信号的码速率为10.23MHz，功率为-133dBm。干扰信号分两种情况进行仿真：

（1）多点频干扰，干扰信号为三个单频干扰，干扰信号功率为-73dBm。干扰抑制前的信号频谱如图3所示，干扰抑制后的信号频谱如图4所示。

图3 多音干扰输入信号的频谱

图4 多音干扰抑制后信号的频谱

（2）窄带干扰，干扰信号为带宽1MHz的窄带干扰，干扰信号功率为-73dBm。干扰抑制前的信号频谱如图5所示，干扰抑制后的信号频谱如图6所示。

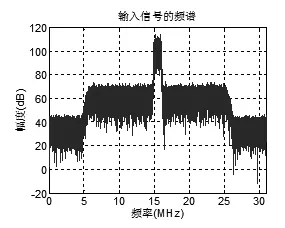
图5 输入信号的频谱

图6 干扰抑制后信号的频谱

通过图3-6的仿真结果可以明显看出，干扰抑制前的尖峰干扰信号在经过加窗重叠相加的频域窄带抑制后，输出信号的频谱中没有了明显的高谱线峰值，无论是单频干扰还是窄带干扰都得到了抑制。

6.小结

本文首先介绍了频域抗窄带干扰的原理，分析了加窗的原因、窗函数的选择、加窗带来的信噪比损失以及解决办法重叠处理，并分析了不同重叠处理方法的效果，最终给出了一套简单易行，性能可靠的重叠加窗抗窄带干扰方案，并通过仿真验证了方案的可行性。

[1]刘毅．GNSS接收机抗干扰技术研究与实现[D]．成都：电子科技大学,2011．

[2]Harris F J．On the use of windows for harmonic Analysis with the discrete Fourier transform [J]． Proceedings of the IEEE,1978,66(1)：5283

[3]毛青春,徐分亮．窗函数及其应用[J]．中国水运,2007,7(2)：230-232．

[4]张斌,孔敏,吴从兵．基于窗函数下频谱泄露的研究[J]．信息化纵横,2009(11)：10-12．

[5]曾祥华,李峥嵘,王飞雪等．扩频系统频域窄带干扰抑制算法加窗损耗研究[J]．电子与信息学报,2004,26(8)： 1276-1281．

[6]孟博,龚文飞,孙昕,等．基于反加窗和重叠选择的窄带干扰抑制方法[J]．导航定位学报,2014,2(2)： 94-96．