基于全矢融合与多维经验模态分解的滚动轴承退化过程频谱结构研究

马艳丽 金 兵 张学欣 韩 捷

郑州大学振动工程研究所，郑州，450001



基于全矢融合与多维经验模态分解的滚动轴承退化过程频谱结构研究

马艳丽 金 兵 张学欣 韩 捷

郑州大学振动工程研究所，郑州，450001

为了识别滚动轴承退化过程，提出一种多维经验模态分解和全矢融合相结合的方法。首先对不同状态的多通道信号同时进行多维经验模态分解，得到一系列多元固有模态函数分量，然后利用互相关系数准则选取最敏感的一阶固有模态函数分量进行全矢包络分析来提取信号的特征。为了验证该方法的有效性，分别对模拟信号和实际信号进行了分析。结果表明此方法在出现故障时，能够很好地表征频谱结构的变化；随着故障严重程度的增加，频谱结构变得复杂，且呈现出了规律性。

多维经验模态分解；全矢融合；频谱结构；轴承退化

0 引言

滚动轴承是重要的机械基础件，广泛用于各个领域[1]，因此对滚动轴承退化状态进行监测与故障程度诊断具有重要意义。滚动轴承的振动信号一般呈现非线性、非平稳特征。经验模态分解(EMD)在处理多通道信号时，把每一个序列作为一个独立变量，单独对每一个序列进行分解，往往会出现尺度排列不确定性问题和同阶尺度频率不一致问题[2]。REHMAN等[3]提出了多维经验模态分解(multivariate empirical mode decomposition，MEMD)方法，对EMD算法进行了改进，使其能同时处理多通道信号，并保证各通道分解得到的固有模态函数(intrinsic mode function,IMF)分量数量一致且对应阶频率成分一致，从而便于多维数据的融合。MEMD方法应用在高速列车转向架、齿轮的故障诊断中时都具有良好的效果[4-5]。文献[6]把噪声辅助MEMD和多尺度形态学相结合，提出了一种滚动轴承故障诊断方法，提高了轴承故障检测精度，但也存在只能处理单通道信号，信息不完善的缺陷。

由于单通道分析存在信息利用不充分的问题，因此韩捷等[7]提出了基于同源信息融合的全矢谱技术，将各个谐波下的主振矢作为此频率处的振动强度，解决了单通道振动信号特征提取不完整的问题。 文献[8]将全矢融合技术应用于WTDS试验台的故障诊断，基于同源信息融合的全矢谱技术能正确地找到预设的故障位置，并准确地判断出故障性质。文献[9]把全矢融合技术和支持向量回归模型相结合，提出了全矢支持向量回归的频谱预测新方法，该方法对汽轮机振动信号频谱结构进行预测时具有较高的预测准确性。

1 MEMD和全矢融合算法

1.1 多维EMD算法

将多维信号沿着不同的方向投影得到多个方向向量，在各个方向上求取信号的包络，通过计算包络信号,可得多维信号的均值。定义q维信号x=(x1，x2，…，xq)，信号x的向量集D中的第l个方向向量Dl=(dl1，dl2，…，dlq)，MEMD的基本算法流程如下[9]：

(1)确定方向向量集D。

(2)在Dl上计算x的第l(l=1，2，…，L)个投影pl(t)，其中，L为方向向量个数，并确定pl(t)最大值所在的时刻tml。

(3)以[tml，x(tml)]为插值节点，获取多维包络线El(t)。

(4)计算包络线均值M(t):

(1)

式中，El(t)为信号x在方向向量Dl上投影的包络线值。

(5)计算剩余量R1(t):

R1(t)=x(t)-M(t)

(2)

式中，x(t)为原始信号,t=1，2，…，q。

如果R1(t)满足多维IMF的迭代终止条件，则定义R1(t)为一阶IMF分量，并以剩余量x(t)-R1(t)为对象重复步骤(2)～(5)，直至分离出下一阶IMF分量。

1.2 互相关系数准则

相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。设有两个序列x=(x1，x2，…，xn)和y=(y1，y2，…，yn) ，则它们的相关系数为

(3)

(1)分别计算nxnor和xnor，nynor和ynor之间的相关系数，并求这些相关系数的平均值，记为on。

(2)分别计算nxabn和xabn，nyabn和yabn之间的相关系数，并求这些相关系数的平均值，记为pn。

(3)计算nxnor和nynor分别与nxabn和nyabn的4个相关系数，并求这些相关系数的平均值，记为qn。

(4)计算敏感系数sn:

sn=(on+pn)/2-qn

(4)

式(4)中，on、pn表明分解得到的IMF分量与初始信号的相关程度，其值越大，IMF分量与初始信号越相似；qn表明同一阶的IMF分量之间的相关性，其值越小，IMF分量变化越大。综合来看，sn越大，这阶的IMF分量越敏感，越能反映频谱变化。

1.3 全矢融合算法

为保证信息的完整性，在旋转机械的同一截面上安装2个相互垂直的传感器来提取振动特征。转子的涡动是由各谐波频率下的组合作用形成的，其涡动轨迹是一系列椭圆。设x、y方向上的数据序列分别为{xi}和{yi}，其构成的复序列为zi=xi+jyi，i=1，2，…，N/2-1；通过傅里叶变换有Zi=ZRi+ZIi，ZRi、ZIi分别为Zi的实部和虚部。

定义椭圆的长轴Rai为主振矢，椭圆的短半轴Rbi为副振矢，αi为主振矢和x轴的夹角,φi为该频率下椭圆轨迹的初相位角。

一般用某个频率上的主振矢代表这个频率上的振动强度。根据傅里叶变换性质可得下式(推导过程参考文献[10])：

(5)

1.4 MEMD和全矢融合算法流程

直接采集到的实际信号一般都会含有噪声，对其处理时，首先用形态学滤波的方法消除部分噪声；然后进行MEMD分解，利用互相关系数准则选取最敏感的IMF分量并对其进行包络解调(包络解调的目的是把与故障有关的信号从高频调制信号中解调出来，从而避免与其他低频相混淆)；最后进行全矢融合分析，提取主振矢。MEMD和全矢融合流程如图1所示。

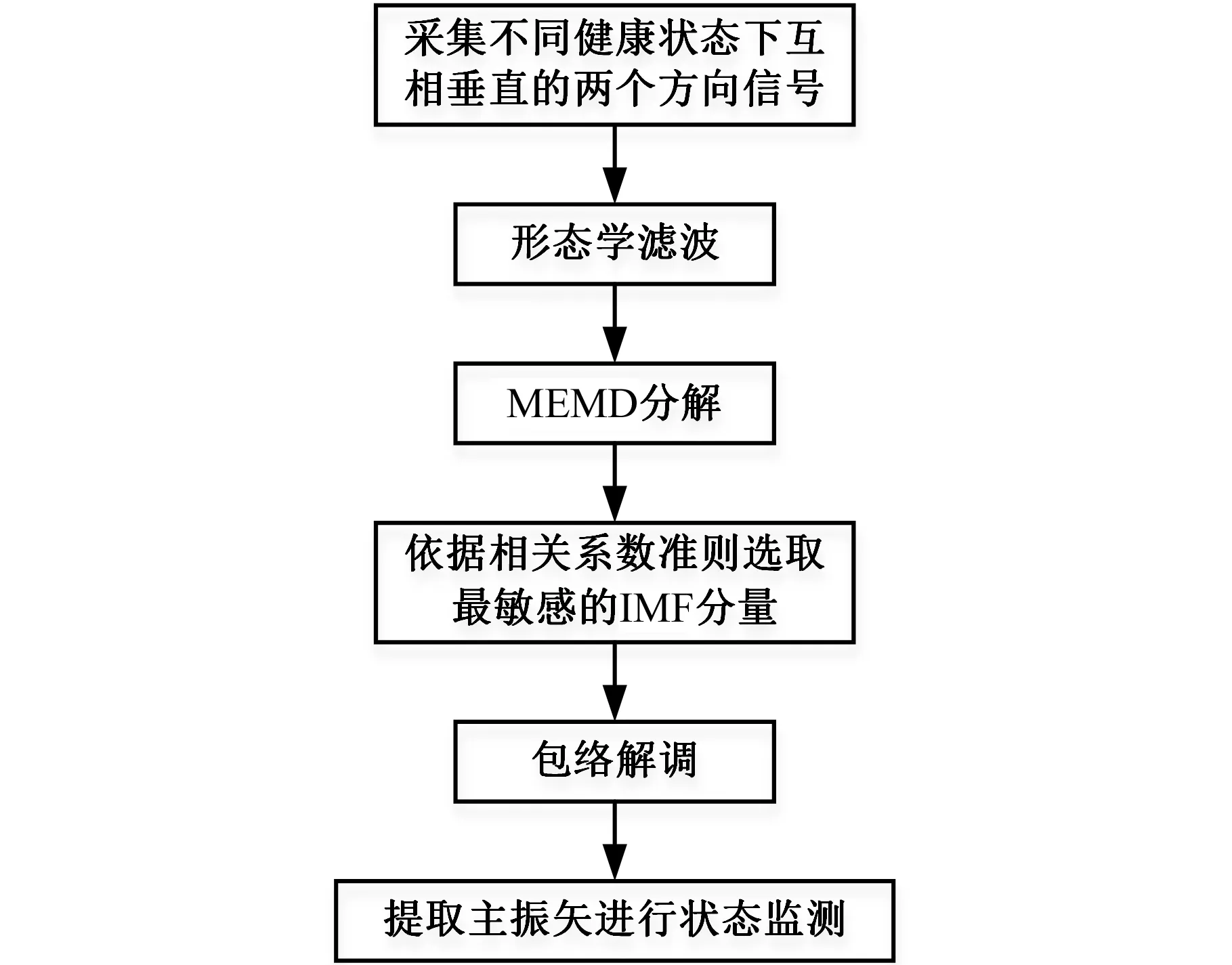
图1 算法流程Fig.1 Flow of the algorithm

2 仿真分析

为了验证MEMD与全矢融合相结合的方法在处理同源信号时的有效性，对模拟信号进行分析。对于滚动轴承信号来说，发生故障时的振动信号呈现调制现象。外圈固定结构的滚动轴承的振动信号为[11]

x(t)=αsin(2πfb)[1+βsin(2πfrt)]

(6)

式中，fb为滚动轴承的内圈通过频率；fr为转子的旋转频率。

基于此，构造如下的模拟加速度信号：

(7)

其中，xnor、ynor是正常运行情况下的两个垂直方向的初始振动信号，xabn、yabn是异常情况下的两个垂直方向的初始振动信号，采样频率fs=1024 Hz，采样点数M=1024。利用MEMD对两个状态对应的双通道仿真信号进行分解，分解结果如图2所示，从图2中可以看出，各通道分解得到的IMF分量数目全为4，并且按照频率尺度对齐，这就为信号融合提供了条件[8]。xnor、ynor第二阶IMF分量IMF2的振幅几乎为零，xabn、yabn的IMF2则有明显的振幅，可以比较完整地体现模拟信号由正常到异常的变化。通常故障信号主要包含在某些IMF分量里，需要从分解得到的前三阶IMF分量中找到最能代表正常与故障状态变化的一阶分量，利用互相关系数准则，得到1～3阶分量的互相关系数，分别为0.18、0.45、0.13，第二阶IMF分量IMF2的互相关系数最大，因此取这一阶进行全矢融合，结果如图3所示。

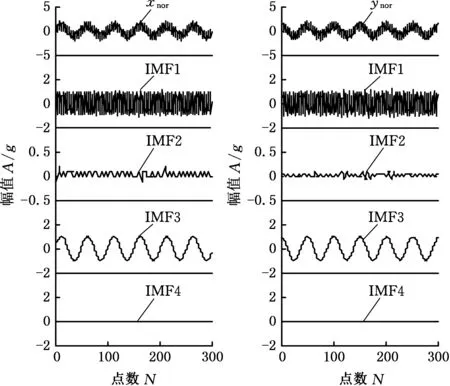
(a)x方向正常运行信号(b)y方向正常运行信号

(c)x方向异常情况信号(d)y方向异常情况信号图2 时间序列(模拟信号)Fig.2 Time series(analog signal)

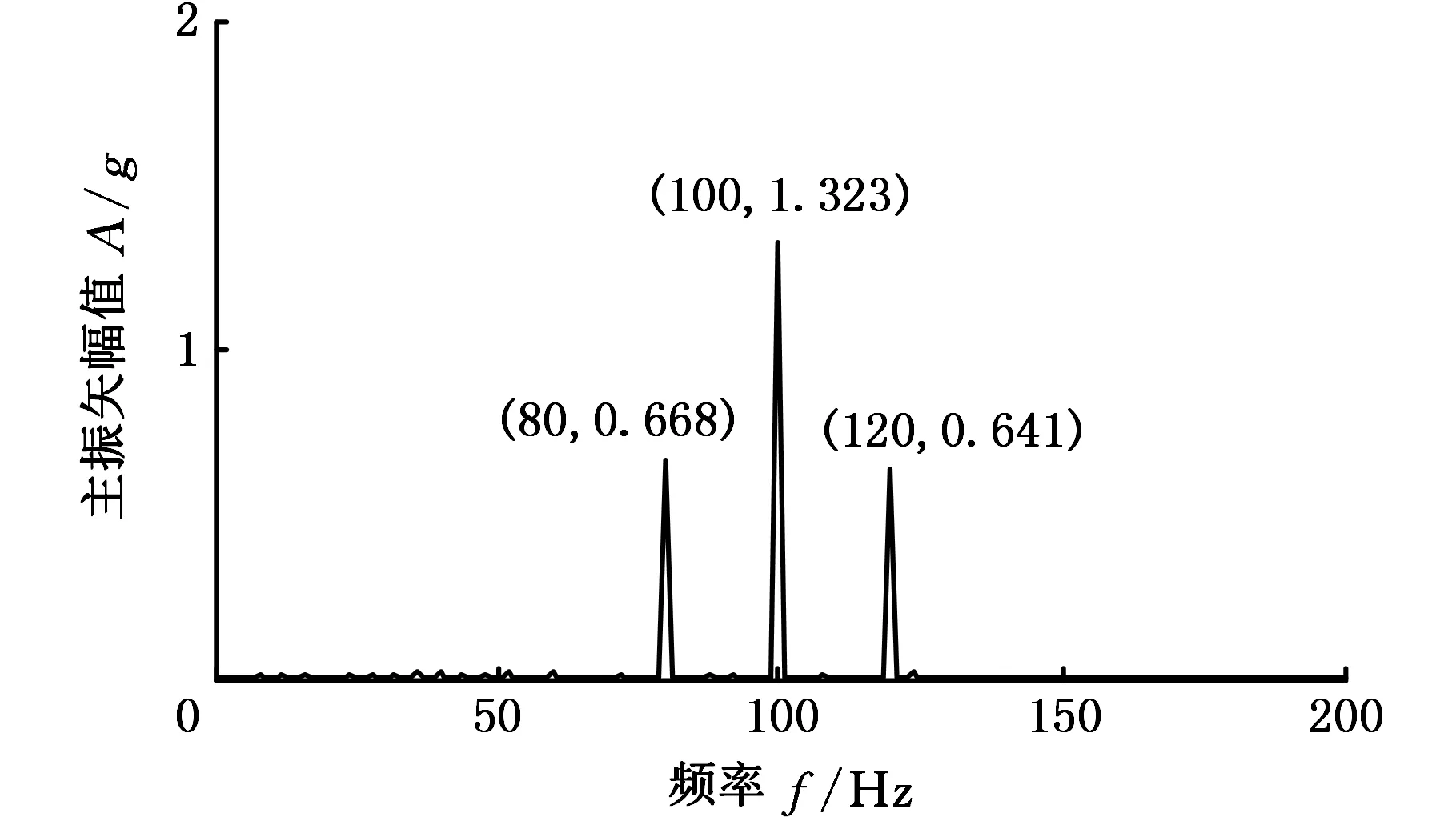
图3 第二阶IMF分量全矢融合图Fig.3 Full vector fusionspectrum of the second IMF component

由于正常情况下的IMF2的振幅几乎为零，故只把异常情况下的IMF2进行全矢融合，从图3中可以看出，100 Hz处振动强烈，且出现了调制现象。异常情况信号xabn、yabn经过全矢融合后，在100 Hz处的振幅是1.323g，调制频率80 Hz、120 Hz处的振幅分别是0.668g和0.641g，这些幅值融合了xabn、yabn的第二阶IMF分量的信息。正常情况到异常情况的变化主要体现在后者出现了调制现象，第二阶分量刚好能够代表信号由正常到异常的频谱结构变化。一般而言，对来自同一截面的双通道信号分别进行频谱分析时，会存在相同频率处的振幅不同的问题，也会存在这两个信号包含频率成分不同的问题，利用全矢融合可以综合双通道的振动信息，能更加全面地反映轴承的运行状态。

3 实例分析

为了进一步验证本文所述方法的有效性，采用由辛辛那提大学智能维护中心提供的滚动轴承数据信号进行分析。轴承实验台的主轴上安装了4个轴承，交流电机通过带传动带动主轴旋转，每个轴承上安装了方向垂直的2个加速度传感器，轴承2、3上加有径向载荷，如图4所示。轴承为ZA-2115双列滚子轴承。轴的转速大约是2000 r/min(33 Hz)，采样频率为20 kHz，采样长度为20 480点，每隔10 min采集一次。在此实验的最后，轴承3出现了内圈故障。根据轴的转速和轴承参数，可计算得出轴承3的内圈故障频率为294 Hz，采集轴承3处于正常状态、轻微故障、中度故障、严重故障的数据进行分析，首先进行形态学滤波以消除部分噪声。然后用MEMD处理，信号分解为12阶IMF分量。依据互相关系数准则，分别计算出每阶IMF分量的互相关系数，如表3所示。

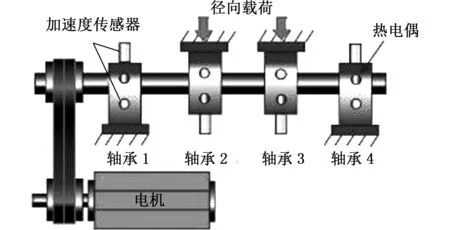
图4 轴承实验台示意图Fig.4 Sketch of bearing test rig

IMF阶数123456互相关系数0．120．300．400．350．240．10IMF阶数789101112互相关系数0．120．05-0．040．30-0．170．02

多通道信号经过MEMD分解后，可以保证各个状态信号对应的IMF分量按照频率尺度对齐，因此，可通过研究所有IMF分量中互相关系数最大的那一阶分量来探究故障发展程度。第三阶IMF分量的互相关系数最大，根据之前的分析可知，在一定程度上，第三阶IMF分量可以代表滚动轴承出现的内圈故障的退化过程。4种状况下的第三阶IMF分量IMF3的时间序列如图5所示，可直观地看出，冲击幅值随故障程度的增加而增大，为了进一步观察不同状态下轴承振动的规律，采用了滚动轴承故障诊断常用的包络分析方法。

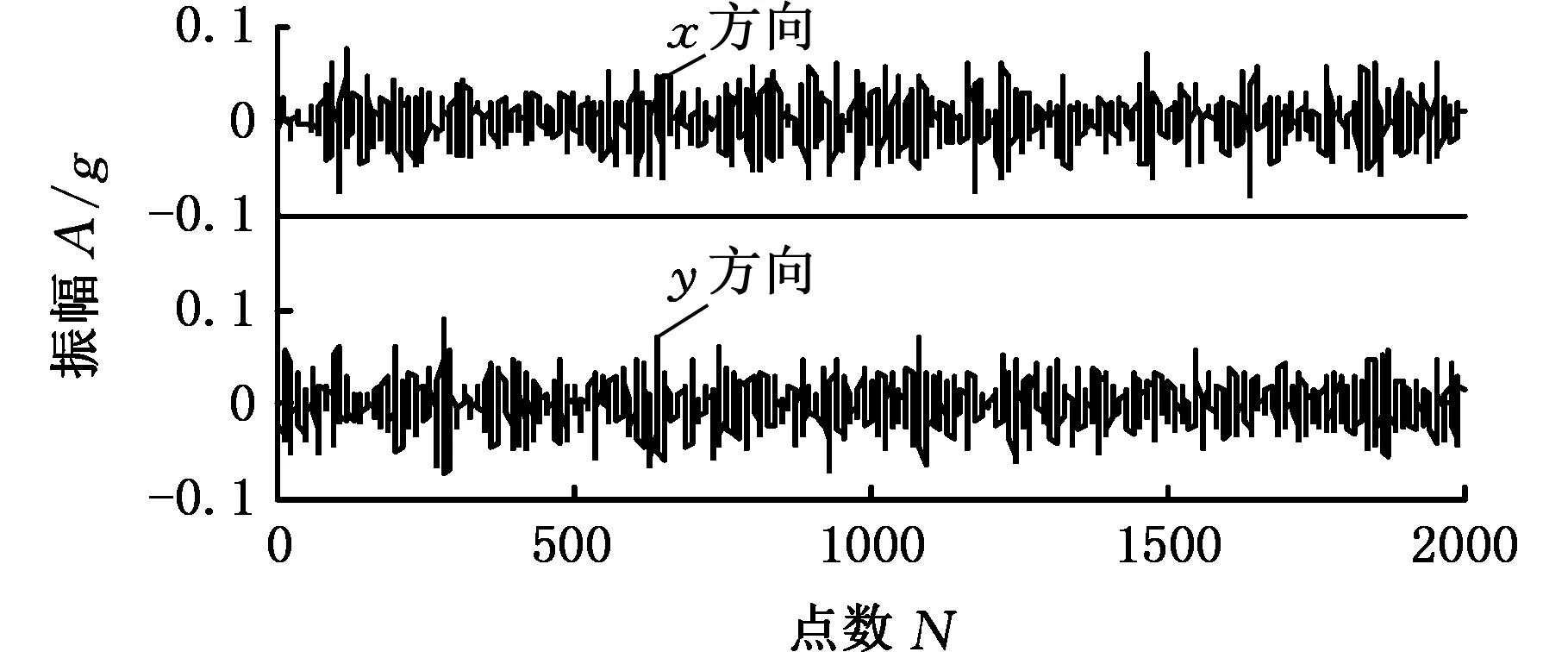
(a)正常运行

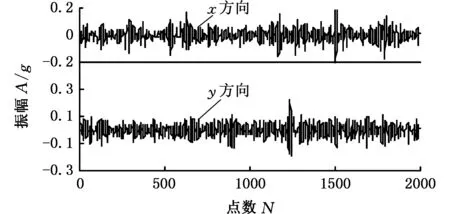
(b)轻微损伤

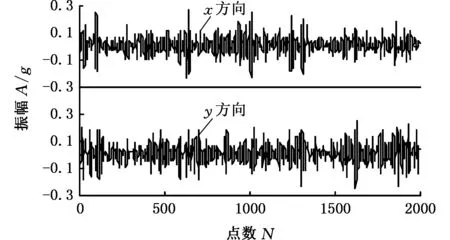
(c)中度损伤

(d)严重损伤图5 第三阶IMF分量的时域图(实际信号)Fig.5 Time-domain figure of the third IMF component

严重故障状态下，对经MEMD分解的x、y方向信号的第三阶IMF分量作包络谱分析和全矢包络谱分析，如图6所示。图6表明，不同故障程度下的两个方向的信息虽然属于同源信息，但是它们所包含的信息并不相同，图6a显示，x方向信号在66 Hz、132 Hz处振幅较小，在261 Hz、294 Hz处振幅较为明显；图6b显示，y方向信号在66 Hz、132 Hz、261 Hz、294 Hz这四处频率下的振动都较强烈，而全矢包络谱则综合了这2个方向的振动信息；图6c表明，对x和y方向作全矢包络分析后，66 Hz、132 Hz处的振幅较大，261 Hz和294 Hz处的振幅比x、y方向上振幅都大。故可以说明，全矢包络谱综合反映了x和y两个方向上的振动信息。

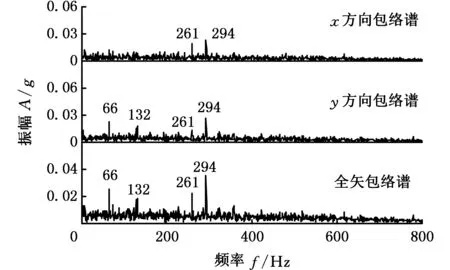
图6 严重故障包络谱Fig.6 Envelope spectrum of serious failure

为了体现滚动轴承退化过程频谱结构的变化，将不同状态下对应的第三阶IMF分量分别进行全矢包络分析。由图7a可以看出，轴承在正常运行情况下，整个频带上的频谱分布很均匀；轻微故障状态下的全矢包络谱(图7b)显示，转轴基频的二倍频66 Hz和轴承内圈故障特征频率294 Hz处的幅值均有所突出，并且在内圈故障特征频率附近出现了明显的基频的调制频率(261 Hz、327 Hz)；随着故障的进一步发展，基频(33 Hz)、基频的二倍频、内圈故障特征频率及内圈故障特征频率的二倍频(588 Hz)处振幅显著增大，并且内圈故障特征频率附近，有更加明显的基频的调制频率，如图7c所示；故障发展到严重程度时，整个频率范围内的振幅明显增大，所有特征频率依然明显，尤其是基频的二倍频、内圈故障特征频及调制频率，如图7d所示。对比这四种状态可知，随着故障程度的增大，整个频带上的振幅增大，基频、故障特征频率及调制频率出现并且幅值增大。

为了对比说明该方法的有效性，对正常状态到严重故障四种情况的初始信号直接进行全矢包络谱分析，结果如图8所示，可以看出，正常情况下的整体振幅较小；轻微故障时，整体振幅有所增大；中等故障时，特征频率下的幅值变得明显；严重故障时，振幅增大明显。整体来看，全矢包络方法的频谱结构的变化不能有效表征轴承的退化过程。全矢MEMD包络分析方法能够有效融合多通道数据，并依据互相关系数，选取对轴承性能退化特征比较敏感的某一阶IMF分量来表征滚动轴承的退化过程，其频谱结构的变化能比较准确、全面地反映滚动轴承性能退化趋势。

(a)正常运行

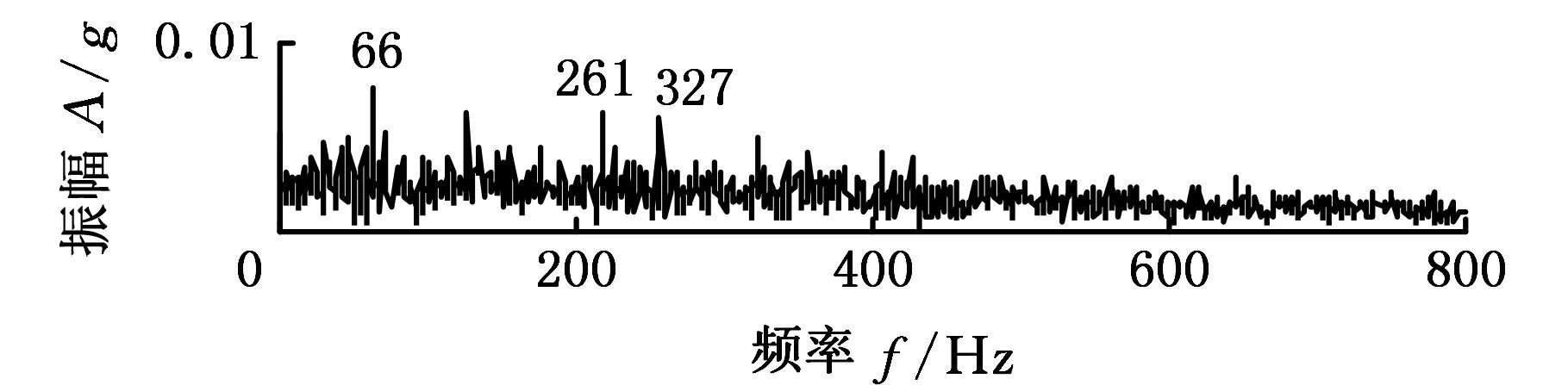
(b)轻微损伤

(c)中度损伤

(d)严重损伤图7 不同状态下包含主要故障信息 的IMF分量全矢包络谱Fig.7 Full vector envelope spectrum of IMF component consisting main fault information in different condition

图8 原始信号全矢包络谱Fig.8 Full vector envelope spectrum of original signal

4 结论

(1)将不同状态下的多通道振动信号用MEMD分解后，可得到相同阶数的IMF分量，且同阶的频率成分一致。利用互相关系数准则选取的最敏感IMF分量可在一定程度上代表原始信号的故障信息。

(2)仿真分析和实例分析表明，随着故障程度的增大，包含主要故障信息的IMF分量的频谱结构变得复杂，且呈现出了一定的规律性。

(3)和传统的全矢包络分析相比，利用互相关系数准则选择出的IMF分量的全矢MEMD包络分析能明显表征滚动轴承在正常、轻微故障、中等故障、严重故障时的频谱结构，其变化更能准确、全面地反映滚动轴承性能的退化。

[1] 杨晓蔚，周宇. 滚动轴承重要性与技术含量纵论[J]. 轴承，2003(1)：35-38. YANG Xiaowei, ZHOU Yu. Importance of Rolling Bearing and Review of Technical Content[J]. Bearing, 2003(1)：35-38.

[2] ZHAO Xiaomin, PATEL T H, ZUO Ming J. Multivariate EMD and Full Spectrum Based Condition Monitoring for Rotating Machinery[J]. Mechanical Systems and Signal Processing, 2012，27(1):712-728.

[3] REHMAN N, MANDIC D P. Multivariate Empirical Mode Decomposition [J]. Proceeding of Royal Society A，2010，466:1291-1302.

[4] 颜云华，吴志丹. 基于MEMD的高速列车转向架故障的排列熵特征分析[J].电子技术应用，2016，42(5)：124-127. YAN Yunhua, WU Zhidan. Feature Analysis of High-speed Train Bogie Based on MEMD and Permutation Entropy[J]. Application of Electronic Technique, 2016, 42(5):124-127.

[5] 张兵，于淑静，董绍江. 基于谱峭度和多元经验模式分解的机械故障诊断[J]. 制造技术与机床，2015(6)：97-101. ZHANG Bing, YU Shujing, DONG Shaojiang. Mechanical Fault Diagnosis Using a Hybrid Spectral Kurtosis and Multivariate Empirical Method Based on Mode Decomposition[J]. Manufacturing Technology & Machine Tool, 2015(6):97-101.

[6] 武哲，杨绍普，任彬，等. 基于噪声辅助多元经验模态分解和多尺度形态学的滚动轴承故障诊断方法[J]. 振动与冲击，2016，35(4)：127-133. WU Zhe, YANG Shaopu, REN Bin, et al. Rolling Element Bearing Fault Diagnosis Method Based on NAMEMD and Multi-scale Morphology[J]. Journal of Vibration and Shock, 2016, 35(4):127-133.

[7] 韩捷，关慧玲，梁川，等. 矢谱：一种实用的旋转机械故障诊断分析方法[J].机械强度，1998，20(3)：212-215. HAN Jie, GUAN Huiling, LIANG Chuan, et al. Vector Spectrum:a Practical Analysis Method of the Rotary Machine Fault Diagnosis[J]. Journal of Mechanical Strength，1998，20(3)：212-215.

[8] 韩捷，张钱龙. 全矢谱技术在WTDS实验台故障诊断中的应用[J].郑州大学学报(工学版)，2017，38(1)：74-77. HAN Jie, ZHANG Qianlong. The Application of Full Vector Spectrum Technology in Fault Diagnosis of WTDS Experimental Platform[J]. Journal of Zhengzhou University (Engineering Science), 2017, 38(1):74-77.

[9] 李凌均，陈超，韩捷，等. 全矢支持向量回归频谱预测方法[J]. 郑州大学学报(工学版),2016,37(3):78-82. LI Lingjun, CHEN Chao, HAN Jie, et al. The Prediction Method of Frequency Spectrum Based on Full Vector Support Vector Regression[J]. Journal of Zhengzhou University (Engineering Science), 2016, 37(3):78-82.

[10] 韩捷，石来德. 全矢谱技术及其工程应用[M]. 北京：机械工业出版社，2008. HAN Jie, SHI Laide. Full Vector Spectrum Technique and Its Application in Engineering[M]. Beijing:China Machine Press, 2008.

[11] 吴斌，王敏杰，康晶，等. 滚动轴承故障振动信号特征与诊断方法[J].大连理工大学学报，2013，53(1)：76-81. WU Bin, WANG Minjie, KANG Jing, et al. Fault Vibration Signal Feature of Rolling Bearing and Its Diagnosis Method[J]. Journal of Dalian University of Technology, 2013, 53(1):76-81.

(编辑 张 洋)

Study on Frequency Spectrum Structure for Rolling Bearing DegradationBased on Full Vector Fusion and MEMD

MA Yanli JIN Bing ZHANG Xuexin HAN Jie

Research Institute of Vibration Engineering,Zhengzhou University,Zhengzhou,450001

In order to recognize degradation processes of rolling bearings, a method combined MEMD with full vector fusion was proposed. Firstly, multi-channel synchronous analyses of vibration signals in different conditions were dealt with MEMD to obtain a series of multivariate intrinsic mode function(IMF) component. Then the most sensitive IMF component was selected by cross-correlation coefficient criterion to do full vector envelope analysis for extracting signal features. Analysis with simulated signal and actual signal was done to test effectiveness of the method respectively. It indicates that the method may reveal changes of frequency structure when faults appear, and shows the regularity that the more serious of the fault conditions is, the more complex of frequency spectrum structure becomes.

multivariate empirical mode decomposition(MEMD); full vector fusion; frequency spectrum structure; bearing degradation

2016-06-07

TH133.3

10.3969/j.issn.1004-132X.2017.14.019

马艳丽，女，1991年生。郑州大学机械工程学院硕士研究生。主要研究方向为设备故障机理及智能诊断技术。E-mail:1076065749@qq.com。金 兵，男，1990年生。郑州大学机械工程学院硕士研究生。张学欣，男，1989年生。郑州大学机械工程学院硕士研究生。韩 捷，男，1957年生。郑州大学机械工程学院教授、博士研究生导师。