气象要素空间插值方法优化研究

彭思岭

（1.广东利通信息科技投资有限公司 智能交通研究院，广东 广州 510641）

气象要素空间插值方法优化研究

彭思岭1

（1.广东利通信息科技投资有限公司 智能交通研究院，广东 广州 510641）

运用反距离加权插值法（IDW）和梯度反距离加权插值法（GIDW）对全国183个气象站的2001年、2002年平均气温进行了内插，并在此基础上进行了幂指数优化和邻近点选择优化。交叉验证结果表明，对于IDW方法，幂指数为3、邻近点选择采用三角网法的插值结果最优；对于GIDW方法，幂指数为2、邻近点选择采用固定数目法的插值结果最优。在幂指数和邻近点选择优化的基础上，比较了IDW方法与GIDW方法的插值结果，考虑经纬度和海拔高程的GIDW方法明显优于IDW方法。在此基础上，提出了基于K-means聚类的空间插值优化方法，实践证明聚类后再插值比直接插值效果更佳，聚类为插值前的数据预处理提供了一种新的思路。

IDW；GIDW；幂指数；聚类

气象要素信息数据是多种地学模型和气候学模型的基础[1]。准确获取气候要素信息数据的方法之一是建立高密度的气象观测站点，但由于经济水平、技术手段和地形条件的限制，很多地方的气象数据获取较困难。为了获取站点外区域的气象数据，研究人员通常将统计学方法与GIS相结合，根据已有站点的观测值估算（气象信息空间插值）全局空间范围内各点位的气象数据。常用的空间插值方法有：反距离加权插值法（IDW）、梯度反距离加权插值法（GIDW）、样条函数插值法、克里金插值法、多项式插值法和趋势面法等[2-3]。本文对IDW和GIDW插值方法的参数进行了优化，得出最优的插值结果，并在此基础上提出了基于K-means聚类的空间插值方法。实验结果表明，该方法优于传统插值方法。

图1 中国气象站点分布图（审图号：GS（2008）1400）

1 数据来源与处理方法

1.1 数据来源

本文所采用的气温数据来自中国气象科学数据共享服务网，中国行政区划数据来自从中国地球科学数据共享网申请的中国1∶400万全要素基础数据；以2001年、2002年全国183个气象站的年均气温数据作为插值分析数据源。183个气象站分布状况如图1所示：数据采用的地理坐标系为GCS_Beijing_1954，投影坐标系为Lambert_Conformal_Conic。

1.2 插值方法

1.2.1 IDW方法

IDW方法是以待插点与实际观测样本点之间的距离为权重的插值方法，离插值点越近的样本点被赋予的权重越大，其权重贡献与距离成反比。其计算公式为[2]：

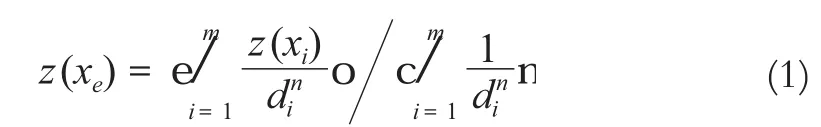
式中，z(xe)为xe处待插点的估算值；z(xi)为xi处的实际观测值；di为xi到xe的距离；m为参与计算的实测样本个数；n为距离的幂，一般取值为2。

1.2.2 GIDW方法

GIDW方法于1998年由Nalder等提出，在IDW方法的基础上，考虑了气象要素随海拔和经纬度的梯度变化。其计算公式为[4]：

式中，Xe、Ye、Ue分别为xe处待插点的经度、纬度和海拔高程值；Xi、Yi、Ui分别为xi处实测样本点的经度、纬度和海拔高程值；Cx、Cy、Cu分别为站点气象要素值与经度、纬度和海拔高程值的回归系数。

1.3 检验方法

采用交叉验证法来验证插值效果[5]，即假定各站点的气象要素值均未知，需通过周围站点的值来估算，再计算所有站点实际观测值与估算值的误差，以此来评估误差方法的优劣。一般情况下采用平均绝对误差（MAE）和插值误差平方和的均方根（RMSIE）作为评估不同插值方法的标准[6]。MAE可评估估算值可能的误差范围，RMSIE可反映利用样点的估算灵敏度和极值效应[7]，MAE和RMSIE的表达式分别为：

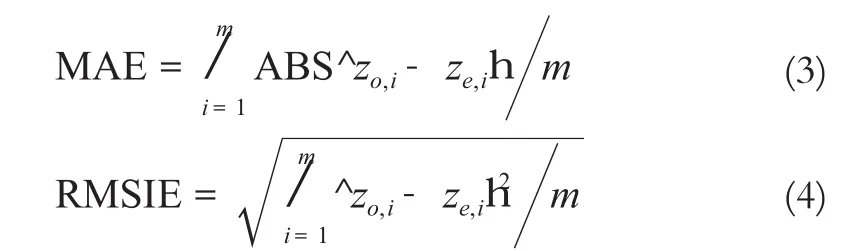
式中，zo,i为第i个站点的实际观测值；ze,i为第i个站点的插值估算值；m为用于参与验证的站点数目。

2 插值结果与对比分析

2.1 幂指数优化

在IDW方法和GIDW方法中，权重的选择直接影响插值的精度，而幂指数的选取直接影响权重的大小，因此幂指数的选取十分关键。国外许多学者取幂指数为2的IDW法对气象数据进行插值[8-9]，本文通过实例验证，幂指数为2并不是最精确的。目前国内外研究者通常采用交叉验证法来验证幂指数的选取对插值精度的影响，以RMSIE作为评估标准，其值越接近0，插值精度越高[10]。根据RMSIE最小的选择标准，幂指数分别选取1～6，采用逐步迭代法对研究区2001 年、2002年气温的幂指数进行筛选，选出最优的幂指数。对于每一个待插值点，均选其周围最近的15 个站点数据进行插值。由表1可知，对于IDW方法，幂指数为3时的插值精度最高；对于GIDW方法，幂指数为2时的插值精度最高。

表1 不同幂指数下的插值精度比较

2.2 邻近点选择优化

在IDW方法和GIDW方法中，邻近点的个数直接影响插值精度。邻近点的选择是空间数据信息处理技术的一个重要研究方向，相关的算法主要可以分为[3]：①固定数目点选择，即选择最近的n个点（n预先指定）。该算法简单且运算矩阵的维数固定，但对于样点分布不均匀可能导致外推。②固定距离点选择，即选择以待预测点为圆心，预先指定的距离为半径的圆所包含的点。该算法遇到样点分布不均匀的情况时，选择的点会过多或过少，且也不能避免外推。③三角网点选择，即选择与离待预测点距离最近的样本点有邻接关系的所有样本点。该算法在处理外围点时会不可避免地出现离待预测点较远的样本点仍被作为插值计算点的情况，明显与实际不符。本文运用IDW方法和GIDW方法对3种邻近点选择方法进行了比较，幂指数选取3，其中固定数目点为15个，固定距离选择东西方向或南北方向最大距离的1/3。3种邻近点选择方法的精度见表2。

表2 不同邻近点选择方法插值精度比较

由表2可知，综合比较2 a的MAE和RMSIE，对于IDW方法，插值精度大小排序为三角网＞固定数目＞固定距离；对于GIDW方法，插值精度大小排序为固定数目＞固定距离＞三角网。当幂指数发生变化时，插值精度大小排序也会发生变化。

2.3 IDW方法与GIDW方法结果比较

在幂指数优化和邻近点选择优化的基础上，运用IDW与GIDW两种方法进行插值。对于IDW法：幂指数取3，邻近点选择采取三角网法的插值结果最优；对于GIDW法：幂指数取2，邻近点选择采取固定数目法的插值结果最优，见表3。

表3 IDW方法与GIDW方法插值精度比较

由表3可知，GIDW方法的MAE、RMSIE明显低于IDW方法，GIDW方法显示了较强的优越性。气温的地理分布及变化受经纬度、地形等因素综合影响，综合考虑经纬度和海拔高程的GIDW插值方法提高了插值精度。MAE和RMSIE可反映插值方法的总体精度，各站点的插值精度可用相对误差（RE，插值估算值与实际观测值之差的绝对值占实际观测值的绝对值的百分比）来评估。以2002年年均气温数据为例，站点相对误差分布见表4。通过比较RE也可得出GIDW方法优于IDW方法的结论，在RE较低的区间（＜10%），GIDW方法的站点百分比高出IDW方法10个百分点；而在RE较高区间（＞50%），GIDW方法的站点百分比低于IDW方法7个百分点。

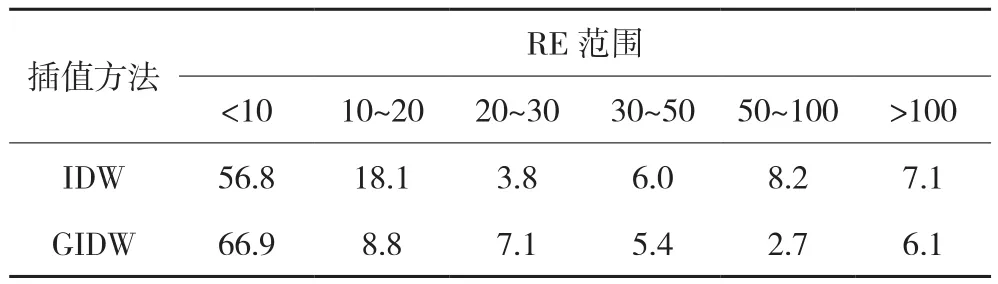
表4 气象站点RE分布/%

3 基于K-means聚类的空间插值方法

根据聚类后结果簇内相似度高、簇间相似度低的原理，将183个气象站分簇，簇内区域用簇内的气象站点数据进行插值，簇外的气象站点数据不参与插值，理论上可获得更高的插值精度。

常用的空间聚类算法很多，本文采用K-means聚类算法，其处理流程为[11]：首先随机选择k个对象，每个对象代表一个簇的初始均值或中心，对剩余的每个对象，根据其与各个簇均值的距离，将其指派到最相似的簇；然后计算每个簇的新均值，不断重复，直到准则函数收敛。

根据中国气温分布的基本特征，大致可划分为东北、华北、西北与南方4个区域，空间聚类后形成空间上的4个簇[12]。本文采用与参考文献[12]中相同的分簇个数，将183个气象站点分成4簇，结果见图2。

图2 气象站点分簇后结果图（审图号：GS（2008）1400）

簇内区域用簇内气象站点进行插值，簇外的点即使距离很近也不参与计算。聚类前与聚类后的精度见表5（以2002年的数据为例）；可以看出聚类后再插值比直接插值具有更高的精度。站点的RE分布见表 6。对于IDW方法，在RE较低的区间（＜10%），聚类后再插值的站点百分比高出直接插值3个百分点；而在RE较高的区间（＞50%），聚类后再插值的站点百分比低于直接插值2个百分点。对于GIDW方法，在RE较低的区间（＜10%），聚类后再插值的站点百分比高出直接插值3个百分点；而在RE较高的区间（＞50%），聚类后再插值的站点百分比低于直接插值0.6个百分点。

表5 聚类前后插值结果比较

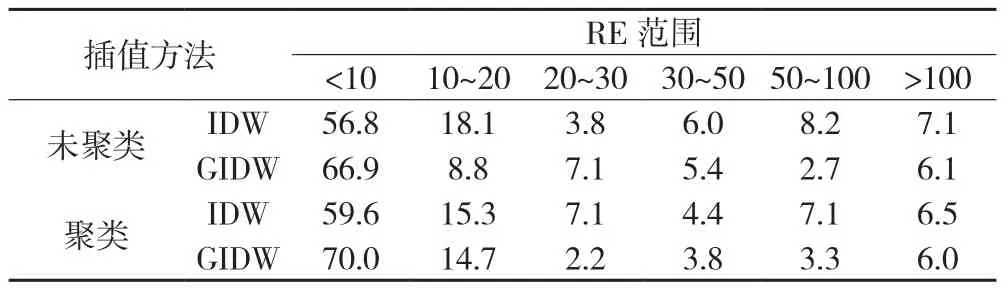
表6 气象站点RE分布/%

4 结 语

本文运用IDW方法和GIDW方法对年平均气温进行插值，并进行了幂指数和邻近点选择的优化；在此基础上比较了两种方法的插值效果，进一步提出了基于K-means聚类的空间插值方法，得出以下结论：

1）许多学者采取幂指数为2的IDW法对气象数据进行插值，本文通过实验验证，幂指数为3时，IDW方法插值效果更好；幂指数为2时，GIDW方法插值效果更好。由此可见，插值方法不同时，最佳幂指数取值也不同。

2）对于本文提到的3种邻近点选择方法，实验结果表明，对于IDW方法，三角网法选择邻近点插值效果最佳；而对于GIDW方法，固定数目法选择邻近点插值效果最佳。

3）GIDW方法的MAE和RMSIE都明显小于IDW方法，可见考虑经纬度和高程的GIDW插值结果优于IDW方法。

4）对全国气象站聚类后再插值，IDW方法和GIDW方法的插值结果均有明显提高。该方法为插值之前气象站点数据的预处理提供了另一种思路。

[1]刘志红,McVicar T R,VanNie T G,等.基于ANUSPLIN的时间序列气象要素空间插值[J].西北农林科技大学学报(自然科学版),2008,36(10):227-234

[2]邬伦,刘瑜,张晶,等.地理信息系统:原理、方法和应用[M].北京:科学出版社,2001:180-191

[3]杜宇健,萧德云.Delaunay-固定距离滑动邻域Kriging算法[J].工程图学学报,2005(2):64-68

[4]Nalder I A, Wein R W. Spatial Interpolation of Climatic Normals: Test of a New Method in the Canadian Boreal Forest[J]. Agricultural and Forest Meteorology,1998,92(4):211-225

[5]Holdaway M R. Spatial Modeling and Interpolation of Monthly Temperature Using Kriging[J].Annals of Physics,1996,6(3):215-225

[6]潘耀忠,龚道溢,邓磊,等.基于DEM的中国陆地多年平均温度插值方法[J].地理学报,2004,59(3):366-374

[7]林忠辉,莫兴国,李宏轩,等.中国陆地区域气象要素的空间插值[J].地理学报,2002,57(1):47-56

[8]Patrick M B. Multivariate Interpolation to Incorporate Thematic Surface Data Using Inverse Distance Weighting(IDW) [J]. Computers & Geosciences,1996,22(7):795-799

[9]Goovaerts P. Geostatistical Approaches for Incorporating Elevation into the Spatial Interpolation of Rainfall[J]. Journal of Hydrology,2000,228(1/2):113-129

[10]Efron B, Gong G.A Leisurely Look at the Bootstrap, the Jackknife, and Cross-validation[J].The American Statistician, 1983,37(1):36-48

[11]Muhammad A, Loftis J C, Hubbard KG. Application of Geostatistics to Evaluate Partial Weather Station Networks[J]. Agricultural and Forest Meteorology,1997,84(3):255-271

[12]刘启亮,邓敏,王佳璆,等.时空一体化框架下时空异常探测[J].遥感学报,2011,15(3):457-474

P208

B

1672-4623（2017）07-0086-04

10.3969/j.issn.1672-4623.2017.07.026

彭思岭，硕士研究生，主要从事GIS的开发研究工作。

2015-09-01。