生物过滤系统中多级混合颗粒群渗流过程分析与完善
2017-08-01王亚军
王 亚 军
(1.兰州理工大学 土木工程学院, 甘肃 兰州 730050; 2.东南大学 土木工程学院, 江苏 南京 210096)
生物过滤系统中多级混合颗粒群渗流过程分析与完善
王 亚 军1,2
(1.兰州理工大学 土木工程学院, 甘肃 兰州 730050; 2.东南大学 土木工程学院, 江苏 南京 210096)
[目的] 准确掌握过滤渗流场的变化规律,为更深刻理解生物过滤系统中流态的变化提供理论参考。[方法] 利用颗粒群加压膨胀理论,基于对流固耦合效应和渗流特性进行研究。[结果] 提出了生物过滤系统渗流过程的4阶段假设,并通过试验验证了变化规律。[结论] 无论在清水和污水渗流过程中都出现的渗透系数由下降到上升再下降变化趋势,是由于颗粒群加压膨胀产生的原因。
生态过滤系统; 渗流过程; 流固耦合; 饱和渗流; 渗透系数
文献参数: 王亚军.生物过滤系统中多级混合颗粒群渗流过程分析与完善[J].水土保持通报,2017,37(3):329-333.DOI:10.13961/j.cnki.stbctb.2017.03.056; Wang Yajun. Analysis and improvement of mixed particle swarm percolation process in biofiltration system[J]. Bulletin of Soil and Water Conservation, 2017,37(3):329-333.DOI:10.13961/j.cnki.stbctb.2017.03.056
由于实际反应器内部水流中颗粒物质与基质之间发生拦截、扩散、黏附等作用所导致的水流迟滞性,以及植物根系、微生物、外部降水和蒸发作用等因素对水流状态的影响,使得实际反应器流态偏离经典理想反应器的程度很大,偏离理想流型的原因主要是在反应器中存在的死角、短路流及沟流等局部堵塞现象[1]。
生态过滤池的堵塞现象在小试、中试和现场使用中都频繁出现[2-4]。过滤系统堵塞问题已成为制约生态过滤技术应用和推广的主要障碍,它解决的好坏直接决定着工程的使用寿命和应用效益。
在下流式生态过滤池中,污染物由上及下依次流经非饱和好氧过滤层、过渡层和饱和含水厌氧淹没层,在底部区域延长水力停留时间来提高微生物浓度,达到提高反硝化处理效果的目的。在这里,出现了两大问题,一是在底部反应后端的反硝化阶段,电子供体成为限速因子,蒙纳仕大学研究团队通过多年研究表明,可以通过在底部淹没区添加碳源等方式弥补这个不足[5-7];二是淹没区的厌氧环境可能加速了系统的渗透堵塞现象,这在其他研究工作中有所阐述[8-9]。但是针对生态过滤系统的渗流过程研究还很缺乏,没有完全掌握渗流场变化规律,同时增加了对水质处理的不可靠性。所以,本文拟对渗滤过程理论加以分析与完善,并以试验进行验证,以期为相关研究提供参考。
1 试验装置参数
生态过滤系统装置箱体材质为无色透明有机玻璃,内部尺寸为500 mm×300 mm×700 mm(长×宽×高),箱体上部布置了一根丰型进水管均匀布水,装置内填料为河砂和砾石,按照澳大利亚FAWB标准指导方法要求的比例装填[10],填充高度为550 mm,各层参数见表1。采用恒流泵(Longer Pump BT100-2 J)保持装置恒定进水,U型液体压力计(BYY型)测定滤层内部压差,TST-70型渗透仪测定填料渗透系数。

表1 生态过滤池模拟参数
2 传统过滤过程理论分析及完善
颗粒以自然状态堆积,颗粒间会留有较多孔隙,若经过适当振实[11],使得颗粒间的孔隙就会大为减少。但颗粒这种有序排列会受到颗粒尺寸、形状及表面特性等多种因素干扰,不易达到最理想的有序排列(即最紧密的堆积)。为了探讨多级混合不规则颗粒群填料堆积体的基本特性以及填充颗粒间隙填充物质的数量和作用等基本规律,首先以球状颗粒材料为基础,作基础计算式的推导和演算。
2.1 颗粒群加压膨胀特性
宏观现象源自内部的力位形和几何构形的调整。Jacques Duran[11]通过二维颗粒球体模型阐明了颗粒间空隙部分在外界作用下发生变化的规律(如图1所示)[11]。
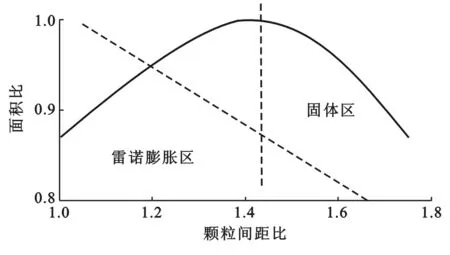
图1 颗粒的加压膨胀特性
可以看出,当上部挤压颗粒时,则颗粒间空隙的面积S随颗粒间距呈现抛物线趋势,面积S存在一个最大值。当颗粒堆积密度很大(即面积S小)时,挤压可使面积S增大,即使得颗粒堆积密度降低。若颗粒堆积密度低到一定程度,则外加作用可造成颗粒密度增大。任何颗粒流动的发生都是以局部颗粒堆积密度的降低(体积膨胀)为条件的。
2.2 Reschke理论计算方法
对于宏观颗粒,经典力学可以给出单个颗粒运动状态的精确解。但是,大量颗粒组成的体系具有特别的性质和运动规律。颗粒群中颗粒无序分布。针对过滤系统内,由不同种类的颗粒混合而成的填料,粒度分布不一定遵守特定的数学方程,由多组分组成的填料层,颗粒分布也是不连续的,不能用传统的数学函数方程来表达。所以需要寻找出一种堆积密度数学模型不受某一固定颗粒分布方程的局限。Reschke理论计算方法[12]在Schwanda模型基础上扩充的功能,此模型不受颗粒分布函数关系的限制,适用于粒度分布不连续的堆积密度的理论计算。这个数学模型除包括了颗粒分布函数关系外,还考虑了颗粒形状和表面粗糙度、细颗粒间干扰作用等因素。
2.2.1 单一粒度理想球状颗粒孔隙体积份数K0K0即为单一粒度颗粒间的孔隙体积数与固体物质体积数的比值。
(1)
式中:K0——单一粒度颗粒孔隙体积份数;ε——孔隙体积数(%);D——堆积密度(与固体物质含量成比例)。
2.2.2 颗粒干扰作用宽度W在颗粒干扰作用比较明显的混合填料体系中,两粒级的粒度比例范围称为颗粒干扰作用宽度,此值取决于基础颗粒粒度与极限颗粒粒度之比。极限颗粒粒度是指刚好没有颗粒干扰作用的粒度。
(2)
式中:W——颗粒干扰作用宽度;Xs——基础颗粒粒度;Xw——极限颗粒粒度。
2.2.3 多级混合颗粒孔隙体积份数h计算基本方程式以由粗颗粒和细颗粒两组分组成的混合颗粒群为基础,Reschke[12]认为,根据粒级之间粒度比例的不同,多级混合颗粒的孔隙体积份数如下:
(3)
式中:hs——基础颗粒级的孔隙体积份数;K0——单一粒径粉体孔隙体积份数;as,i——i粒级的颗粒干扰系数;Vi——i粒级所占整个固体体积份数;n——粒级组分数。
编制数学模型的基础即是K,W,Xi/Xs和系数as,i之间的数学关系,可用图2表示[13]。
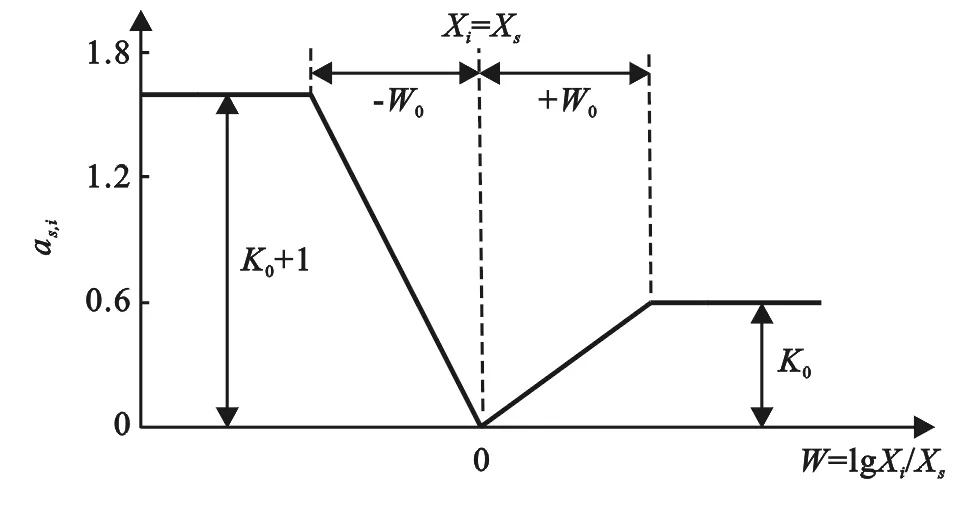
注:K0为单一粒径粉体孔隙体积份数;as,i为i粒级的颗粒干扰系数;Xi为i粒级的颗粒粒度;Xs为基础颗粒粒度;W0为单一粒的颗粒干扰作用宽度;W为颗粒干扰作用宽度。
图2 颗粒干扰系数as,i与Xi/Xs的关系
图中以Xi=Xs为分界点,左侧为Xi
当某一粒级作为基础颗粒时其他各粒级均为填充颗粒,由基础颗粒的孔隙体积份数K0减去其他各级填充颗粒的相应固体体积份数Vi,即可得出基础颗粒级的孔隙体积份数hs值,如式(3)所示。
2.3 过滤渗流过程机理分析与完善
2.3.1 过滤渗流过程理论 早在1958—1973年敏茨和艾弗斯位学者就滤料层的过滤过程进行了长期争论[14],且至今没有统一的定论;在这期间,1965年Jones等[8], Kehat等[15]提出了在好氧条件下基质堵塞过程经历了3个阶段,第1个阶段是渗透速率接近系统开始运行时的渗透速率,但呈现逐渐下降趋势;第2阶段是一个实质性的平稳下降阶段;第3阶段是直至持续堵塞发生。而在厌氧条件下,没有以上的第2阶段,第1和第3阶段也不是很明显辨别。
2.3.2 过滤渗流过程假设 经典渗流力学一般假定流体流经的固体介质是完全刚性的,即在孔隙流体压力变化过程中,固体骨架不产生任何弹性或者塑性变形。但是,在实际的渗流过程中,由于孔隙流体压力的变化,一方面要引起多孔介质骨架有效应力变化,由此导致渗透率的变化,另一方面,这些变化又反过来影响孔隙流体的流动和压力的重新分布,这就必须让研究者考虑孔隙流体在介质中的流动规律的同时,也要考虑渗流场对介质本身变形造成的影响。所以,仅从污染介质干扰滤料层角度来分析水体流经填料的渗滤过程是不充分的,作者认为还需要考虑运行过程中孔隙的三维几何形态变化。为此本文对生物过滤系统堵塞过程进行了重新诠释。提出2种情况的假设:
第一,清水渗流过程经历4个阶段,第1阶段是渗透系数逐渐下降趋势;第2阶段是渗透系数有急剧上升势头;第3阶段是渗透系数有稍微下降趋势;第4阶段渗透系数平稳不再发生大的波动变化。
第二,污水渗流过程经历4个阶段,第1阶段是渗透系数逐渐下降趋势;第2阶段是渗透系数有急剧上升势头;第3阶段是渗透系数开始迟缓下降趋势;第4阶段是渗透系数持续下降,逐渐进入堵塞阶段。可能的原因:第1和第2阶段,颗粒群紧密堆积下受到水压力作用导致空间构造改变,孔隙压缩,同时污水携带的颗粒物通过截留、沉淀、扩散和横向迁移吸附在滤料表层,微生物为生长挂膜阶段,生长量大于脱落量;第3阶段,由于颗粒加压膨胀特性,颗粒空间出现由小变大的趋势,随后又挤压变小,这期间受到外加水力剪切和颗粒摩擦等的作用,滤料表层的颗粒物和生物膜发生脱落;第4阶段,颗粒构造基本稳定,随滤料层深度的加大,脱落下的颗粒物和生物膜持续累积,在滤料层局部不同程度地形成不透水区域。
3 结果与分析
3.1 混合填料孔隙率计算
首先对反应器运行初期混合填料的孔隙率进行理论计算,过滤系统内填料是由8种不同粒级组成的颗粒群混合而成,在研究运行过程中多级混合填料颗粒间孔隙体积的变化,首先需较为科学地计算出混合填料的孔隙体积,孔隙体积间接表明了水流孔道的变化情况。
3.1.1 多级混合颗粒孔隙体积份数计算 各平均粒度X分别为0.25,0.50,1.00,2.00,3.00,6.00,12.00,15.00 mm;试验测得各粒度的孔隙率ε分别为29.5%,31.5%,32%,33.6%,35.8%,37%,43%,44.5%;各粒级孔隙体积分数K0,i根据公式(1)计算所得分别为41.84%,45.99%,47.06%,50.60%,55.76%,58.73%,75.44%,80.18%;颗粒干扰作用宽度W0为0.9。以每一粒级都分别作一次基础颗粒,计算出相应的as,i与Vi的乘积,结果如表2所示。
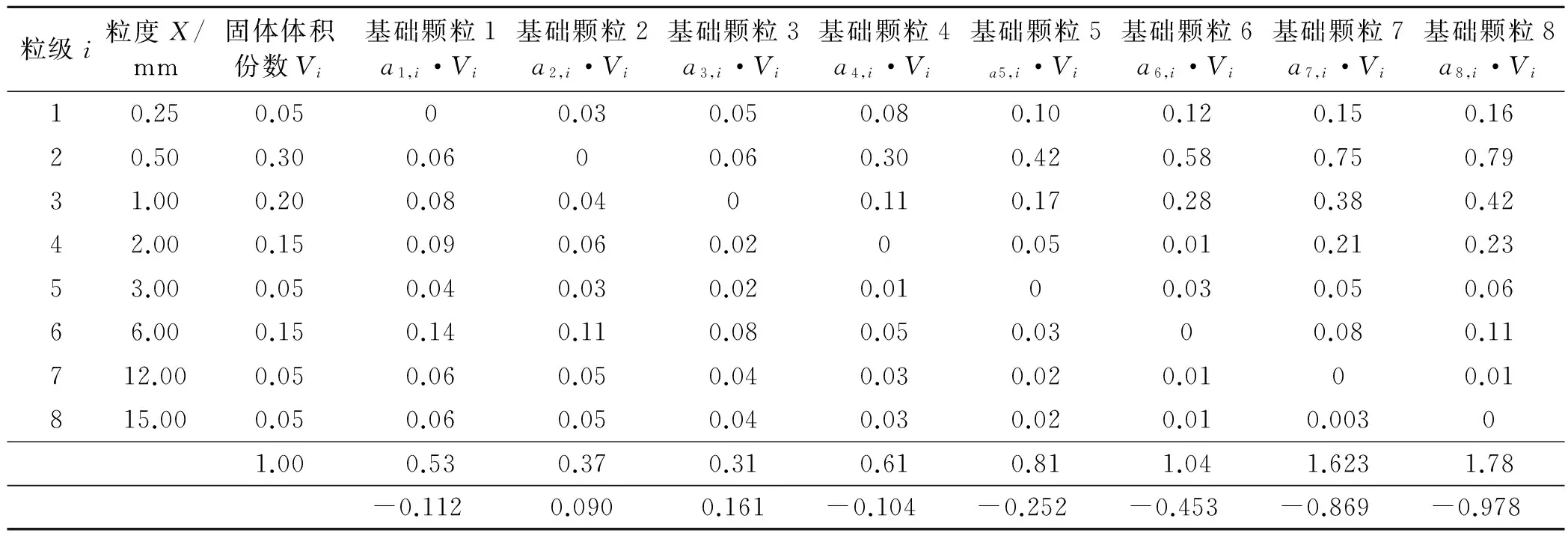
表2 孔隙体积份数计算模型
3.1.2 混合填料孔隙率计算 从表2中找出基础颗粒孔隙体积份数最大(hs值)的粒级作为混合粉体堆积密度D的计算依据,可以看出,粒级3的hs最大,为0.161,且有:
则得到混合填料的堆积密度为0.861 3。最终得出混合填料的孔隙率为13.87%。通过表观密度和堆积密度的测定计算出混合填料的孔隙率为14.54%,相对误差为4.61%,因此说明按以上方法计算出混合填料孔隙率是较为精确的。
3.2 渗透特性测定
两套生态过滤池同步进行清水和污水渗透试验,在1.0 m3/(m2·d)进水负荷水平下连续运行。得出相同水力负荷条件下渗透系数在时间序列上的变化情况,如图3所示。
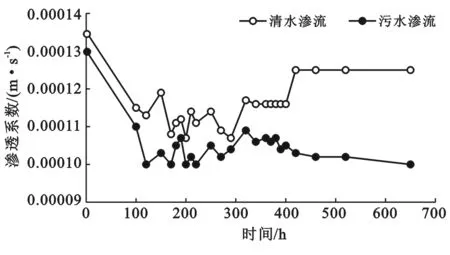
图3 渗透系数-时间的关系曲线
在运行初期,清水和污水通过介质的渗透系数后表现出总的下降趋势;这是由于在试验装置持续运行导致原有颗粒群间的构造发生变化,产生颗粒群骨架流变和局部孔隙塌陷的现象,新形成的空隙比原来的空隙要小,水流在其中流动水头损失增大,因此渗透系数减小。随时间推移,清水和污水流经介质的渗透系数均表现出波动上升,这是因为颗粒间空隙变大的区域多于塌陷区域,水流通道变宽,渗透系数呈现曲折爬上趋势。在长期连续进水后,两者出现了不同的变化趋势,清水流经介质时,渗透系数先略有下降后平稳,这是由于颗粒间孔隙基本全部塌陷,渗透系数下降至稳定,当水头压力不足以使颗粒介质之间的结构发生新变化,渗透水流在其中流动的路径变得较为稳定,渗透系数较为平稳。污水流经介质时,渗透系数逐渐下降,这是由于随运行时间的延长,根据热力学基本原理,一个封闭体系总会趋于自由能最小的状态,最终都会通过扩散等热运动,使系统的熵达到最大,形成均匀分布的平衡态,颗粒构造最终稳定。此时,污水携带的颗粒污染物和逐渐成熟的生物膜成为制约渗透的限制因子,致使产生堵塞现象发生。这也支撑了过滤堵塞过程假设的成立。
4 结 论
(1) 借助颗粒群加压膨胀理论,基于对流固耦合效应的思考和渗流特性的研究,提出了生态过滤系统渗流过程的4阶段假设:清水渗流经历渗透系数下降、上升、下降和平稳4阶段过程;污水渗流经历渗透系数下降、上升、平稳和下降4阶段过程。
(2) 借助Reschke理论计算方法对多级混合填料孔隙率进行了理论计算,并与实测数据对比,相对误差为4.61%,因此说明按此方法计算出混合填料孔隙率较为精确。
(3) 通过连续运行下生态过滤池渗透系数的测定,其变化规律与假设渗流过程相同,并通过试验数据支撑了过滤堵塞过程假设的成立。
[1] 许保玖,龙腾锐.当代给水与废水处理原理[M].2版.北京,高等教育出版社,2000,78.
[2] Coustumer S L, Fletcher T D, Deletic A, et al. The influence of design parameters on clogging of stormwater biofilters: A large-scale column study [J]. Water Research, 2012,46(20):6743-6752.
[3] Kandra H, Mccarthy D, Fletcher T D, et al. Assessment of clogging phenomena in granular filter media used for stormwater treatment [J]. Journal of Hydrology, 2014,512(4):518-527.
[4] Coustumer S L, Fletcher T D, Deletic A, et al. Hydraulic performance of biofilter systems for stormwater management: Influences of design and operation[J]. Journal of Hydrology, 2009,376(1/2):16-23.
[5] Zinger Y, Blecken G T, Fletcher T D, et al. Optimising nitrogen removal in existing stormwater biofilters: Benefits and tradeoffs of a retrofitted saturated zone[J]. Ecological Engineering, 2013,51(2):75-82.
[6] Glaister B J, Fletcher T D, Cook P L, et al. Co-optimisation of phosphorus and nitrogen removal in stormwater biofilters: The role of filter media, vegetation and saturated zone [J]. Water Science & Technology, 2014,69(9):1961-1969.
[7] Payne E G, Fletcher T D, Russell D G, et al. Temporary storage or permanent removal? The division of nitrogen between biotic assimilation and denitrification in stormwater biofiltration systems[J]. PloS one, 2014,9(3):1-12.
[8] Jones J. H. and Taylor G. S. Septic tank effluent percolation through sands under laboratory conditions[J].Soil Science,1965,99(5):310-309.
[9] Blazejewski R, Muratalazejewska S. Soil clogging phenomena in constructed wetlands with surface flow[J]. Water Science and Technology, 1997,35(5):183-188.
[10] Payne E G I, Hatt B E, Deletic A, et al. Adoption Guidelines for Stormwater Biofiltration Systems[M]. Melbourne, Australia: Cooperative Research Centre for Water Sensitive Cities, 2015.
[11] Duran J. Sands, Powders, and Grains: An Introduction to the Physics of Granular Materials[M]. New York: Springer, 2000.
[12] Reschke T. Schriftenreihe der zementindustrie62/2006[M]. Dusseldorf: Verlag Bau Technik GmbH, 2000.
[13] 乔龄山.水泥堆积密度理论计算方法介绍[J].水泥,2007(7):1-7.
[14] 李圭白,张杰.水质工程学[M].北京:中国建筑工业出版社,2005:148-149.
[15] Kehat E, Lin A, Kaplan A. Clogging of filter media[J]. Industrial & Engineering Chemistry Process Design and Development, 1967,6(1):48-55.
Analysis and Improvement of Mixed Particle Swarm Percolation Process in Biofiltration System
WANG Yajun1,2
(1.SchoolofCivilEngineering,LanzhouUniversityofTechnology,Lanzhou,Gansu730050,China; 2.SchoolofCivilEngineering,SoutheastUniversity,Nanjing,Jiangsu210096,China)
[Objective] To accurately master the variation law of the filtration flow field, and to provide a theoretical reference for the deeper understanding of the change in the flow in the biofiltration system. [Methods] Based on the particle swarm pressure expansion theory, characteristics of the infiltration were studied mainly in consideration of the fluid-solid coupling effect. [Results] A four stage hypothesis in the percolation process of the biofiltration system was put forward and verified by the experiment. [Conclusion] Either for the process of water seepage or sewage seepage, the permeability coefficients changed from falling to rising and then decreasing, which is caused by the particle swarm pressure expansion.
biofiltration; infiltration process; fluid-structure interaction; saturated flow; permeability coefficient
2016-10-30
2016-11-12
“十二五”国家科技支撑计划重大项目“长三角快速城镇化地区美丽乡村建设关键技术综合示范”(2015BAL02B05); 江苏省重大科技专项课题(BE2015356-2); 江苏高校优势学科建设工程资助项目(CE02-1-1); 甘肃省高等学校科研项目(2016B-026)
王亚军(1979—),男(汉族),山西省介休市人,副教授,主要从事污水资源化利用研究。E-mail:wyj79626@163.com。
B
1000-288X(2017)03-0329-05
X502
