黏弹性土中深埋球形沼气池的动力特性★

钱长根 向天勇 闻敏杰*

(嘉兴职业技术学院，浙江 嘉兴 314036)



黏弹性土中深埋球形沼气池的动力特性★

钱长根 向天勇 闻敏杰*

(嘉兴职业技术学院，浙江 嘉兴 314036)

采用解析方法在频率域内研究了周期荷载作用下黏弹性土体中深埋球形沼气池简谐振动特性。将模具结构分别视为均匀弹性介质和薄壁壳体结构，基于弹性和Flügge理论，给出了分数导数黏弹性土中深埋球形沼气池振动响应的解析表达式。根据连续性边界条件，确定了相关待定系数的表达式。在此基础上，对比分析了均匀弹性介质和薄壁壳体时系统动力响应的结果，并考察了分数导数本构参数、土体和模具各参数对系统动力特性的影响。结果表明：两种模型下模具结构的振动响应存在较大差异。

沼气工程,黏弹性土,球形沼气池,简谐振动,解析解

0 引言

深埋地下球形沼气池不仅具有球形口小、密闭性好和产气量高的优点，而且池中沼液发酵充分，不易产生结壳，同时受外界环境温度影响小[1]。因此，在我国农村得到普遍的应用和推广。

沼气池的振动响应在池壁抗震、抗爆设计和模具结构稳定性等领域中具有广泛的运用背景，一些学者对此进行了深入研究。Forrestal和Sagartz[2]研究了Heaviside荷载作用下均匀弹性土体中薄壁球壳和圆柱形壳体的动力响应。Duffey[3]采用Laplace变换技术，得到了脉冲荷载下黏弹性和黏塑性球形模具结构的瞬态动力响应。Glenn[4]将土体视为线弹性介质，推导了Heaviside荷载和脉冲荷载下深埋球形沼气池的振动响应。张庆元等[5]以位移为未知量，研究了爆炸荷载作用下球形空腔的瞬态响应。Liu Ganbin等[6]研究了黏弹性饱和土和薄壁球壳结构系统的耦合振动特性。韩同春和刘干斌[7]研究了任意荷载下无限大黏弹性体内球壳的动力响应。上述都忽略了模具结构的厚度。为了得到精确解，Auslender[8]将模具结果视为弹塑性材料，得到了爆炸荷载作用下球形沼气池的数值近似解。

土体具有黏弹性性质，研究表明分数导数本构模型可更好地刻画其蠕变特性[9,10]。该本构模型早期在航空材料、混沌和湍流、材料松弛、机器人控制、生物材料、随机游走等工程领域[11]。但是，基于分数导数模型建立动力学方程为奇异性积分—偏微分方程，其理论分析和数值计算存在诸多困难[12]，在土体动力特性方面的研究不多见[13,14]。尤其是研究球形沼气池的动力特性在国内外均无相关报道。

然而，池内气体发酵产生和用户消耗，使池内气压反复变化而产生压力，这种应力均匀作用于池壁内侧，即可等效为周期荷载[15]。本文首先将土体视为具有分数阶导数本构的黏弹性体，根据黏弹性理论推导了沼气池周围无限大分数导数黏弹性土的位移和应力表达式。再次，将模具结构分别视为均匀弹性介质和薄壁壳体结构，根据弹性动理论[16]和Flügge理论[17]得到了模具结构振动响应的解析解。其次，根据模具结构和土体接触面处位移和应力连续等边界条件，得到了相关待定系数的具体表达式。然后，将该文解答进行了退化，通过与已有成果对比，体现了本文计算结果的正确性。最后，考察了分数导数本构参数，模具和土体各参数对系统振动响应的影响，为地下球形沼气池的设计和施工提供了一定的理论依据。黏弹性土中球形沼气池见图1。

1 数学模型

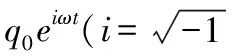
2 土体控制方程的建立及求解

球对称情形下，具有分数导数本构黏弹性模型的应力—位移本构关系为[14]:

(1)

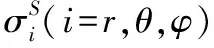
(2)

在动力荷载作用下，根据弹性动理论，土体的动力方程为[16]:

(3)

将式(1)代入式(3)得:

(4)

引入如下势函数:

(5)

对于稳态振动，设:

(6)

引入如下无量纲量和常数:

(7)

将式(5)～式(7)代入式(4)，得:

(8)

其中，

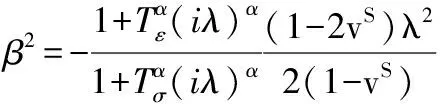
式(8)易解得:

(9)

其中，A,B均为待定系数，由边界条件来确定。

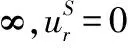
(10)

将式(5)代入式(10)得:

(11)

由式(11)代入式(1)，得:

(12)

3 模具结构运动方程建立及求解

3.1 第一类模具结构方程

将球形沼气池模具结构视为均匀弹性介质，假定模具和土体界面处完全紧密接触，无相对滑移，即满足应力和位移连续。在动力荷载作用下，模具结构的运动方程为[16]：

(13)

本构关系:

(14)

将式(14)代入式(13)得:

(15)

(16)

将式(16)代入式(15)得:

(17)

其中，

(18)

式(17)可易解得:

(19)

其中，C5，C6均为待定系数，由边界条件来确定。

将式(19)代入式(16)得:

(20)

于是，由式(14)可知径向应力为:

(21)

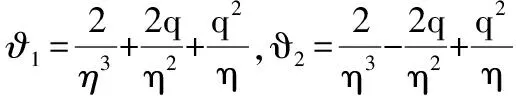
满足如下边界条件：

1)在模具结构和土体界面处r=R2(η=1)位移连续，即:

(22)

2)在模具结构和土体界面处r=R2(η=1)应力连续，即:

(23)

3)在模具结构和土体界面处r=R1(η=1)内荷载等于模具结构的径向应力，则:

(24)

结合式(22)～式(24)得待定系数A,C5，C6的具体表达式为：

(25)

其中，

a1=-(1+β)e-β,

a2=(1+q)e-q,

a3=(1-q)eq,

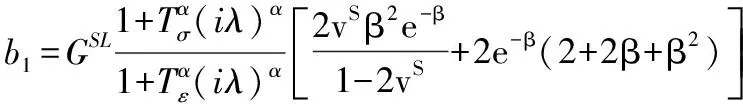
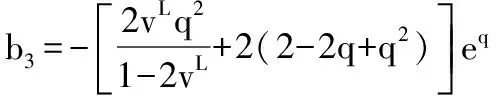
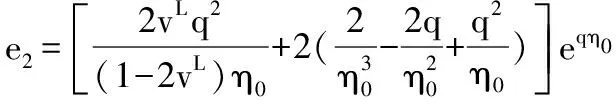
3.2 第二类模具结构方程

由于模具结构的厚度远小于球形沼气池的半径，因此，可假定模具结构和土体的界面处r=R2与中曲面半径r=a影响很小[6]。根据Hamilton原理，模具结构的运动方程为[7]：

(26)

其中，Qa为净压力。

1)在模具和土体接触面上r=R2(η=1)应力协调，即:

(27)

2)在模具和土体接触面上r=R2(η=1)位移连续，即:

(28)

式(26)和式(12)代入式(27)，式(28)得:

(29)

其中，

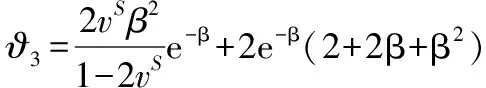
4 与已有成果对比分析

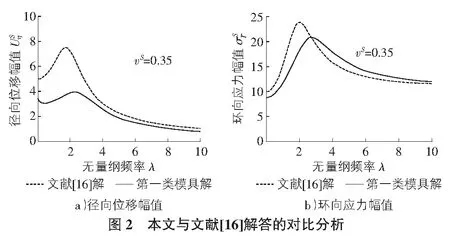
为了验证本文计算结果的正确性，首先，与文献[16]作对比，该文忽略了模具结果的影响，建立了一般理想弹性土体中球形沼气池的动力特性。将经典弹性本构代入式(3)，且令土体和模具结果的材料参数完全相同，即可将本文退化到文献[16]的解答。参数取值：η=1，vS=0.35，ρLS=1.5，GSL=0.05，vL=0.25，δ=0.005，Tσ/Tε=3，Tε=10，α=0.05。

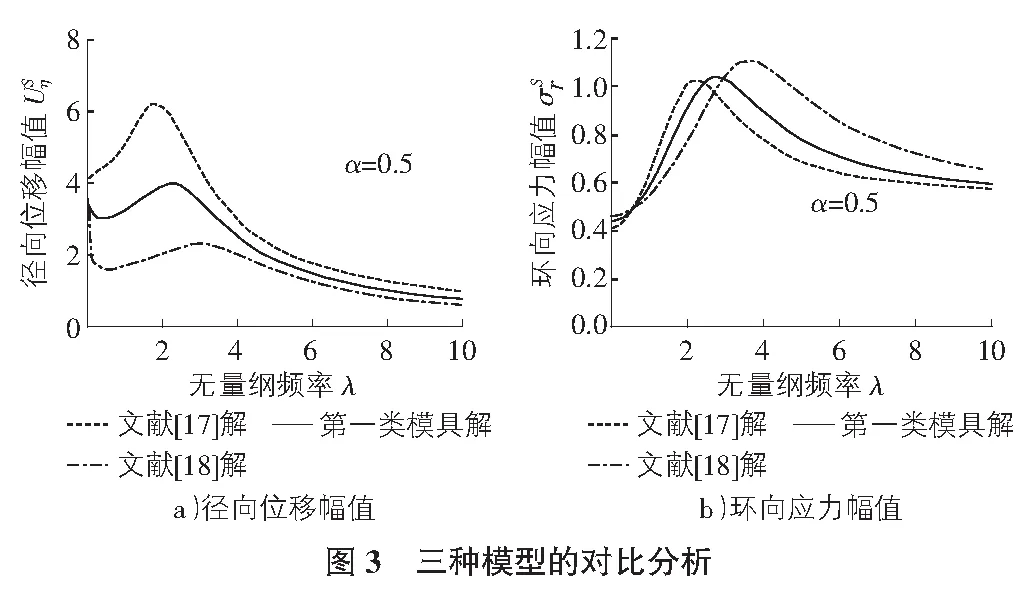
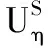
5 数值算例及图形分析

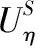
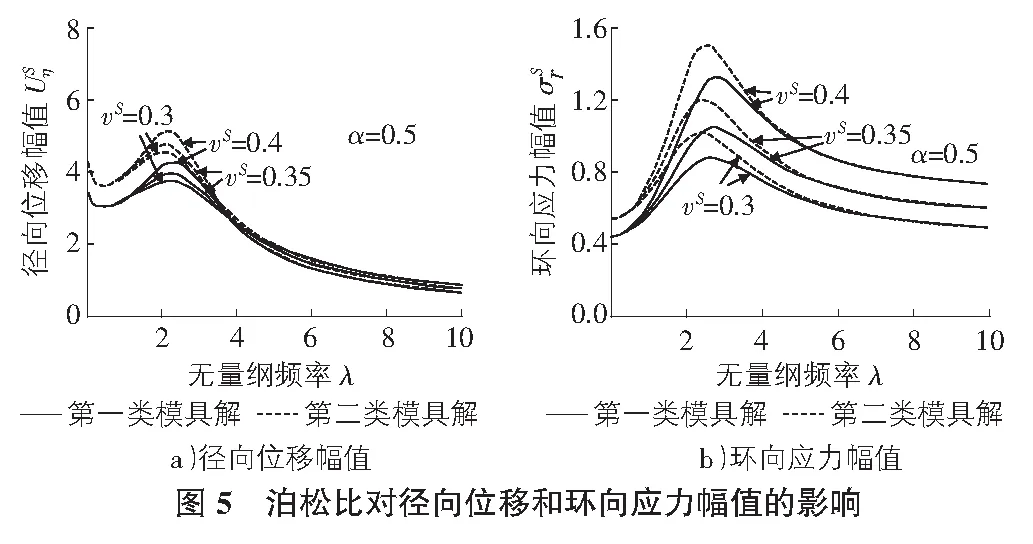
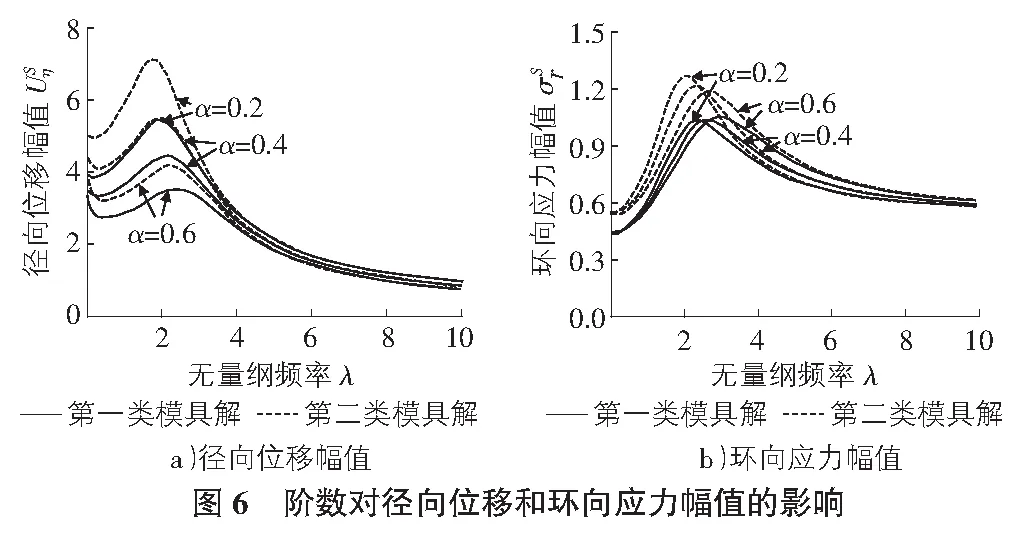
图4反映了土体和模具结构的剪切模量比变化时径向位移和环向应力幅值随频率λ的变化规律曲线。可见，当模量比GSL较小时，第一类模具模型条件下系统的位移幅值与第二类模具模型时土体的位移幅值存在很大差异，后者系统产生的共振效应要显著。随着GSL的增加，两者的位移幅值差异较小。球壳模具结构时的环向应力幅值明显大于均匀弹性介质时的应力幅值。随着频率λ的增加，两者差异减小，且随着模量比GSL的增加，位移和应力幅值明显减小。

图5给出了土体泊松比vS变化对径向位移和环向应力幅值的影响规律曲线。随泊松比vS的增加，径向位移和环向应力幅值逐渐增大。在较高频率时两类模具结构条件下的位移和应力幅值差异很小。

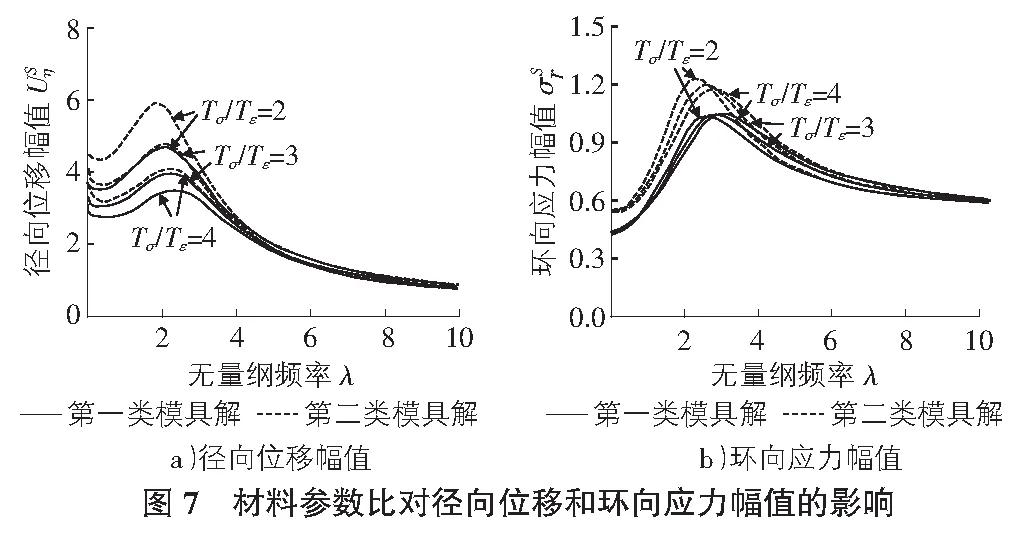
图6反映了分数导数阶数α对径向位移和环向应力幅值的影响。可见，随着阶数α的增加，径向位移和环向应力幅值明显减小，且系统共振效应减弱。图7给出了本构模型的材料参数比Tσ/Tε变化时径向位移和环向应力幅值随频率λ的影响曲线。可见，随着材料参数比Tσ/Tε的增加，径向位移和环向应力幅值明显减小，这是因为材料参数比Tσ/Tε增加时土体的阻抗增大所造成的。

6 结语

本文采用解析方法在频率域内研究了均布内压作用下黏弹性土体中深埋球形沼气池简谐振动特性，考察了相关物性和几何参数对系统动力特性的影响，得到了如下结论：

1)在Tσ/Tε=3条件下，具有球形沼气池分数导数黏弹性土的稳态响应大于经典黏弹性土的稳态响应，而小于经典弹性土的振动响应；

2)球壳模具结构模型条件下，球形沼气池的稳态响应明显大于均匀弹性介质模型条件下球形沼气池的稳态响应；

3)当模量比较小时，第一类模具模型条件下系统的位移幅值与第二类模具模型时的位移幅值存在很大差异，随着GSL的增加，两者差异很弱；

4)随着土体材料泊松比vS的增加，系统的位移幅值和环向应力幅值逐渐增大；

5)随着阶数α的增加，径向位移和环向应力幅值明显减小，且系统共振效应减弱；

6)随着材料参数比Tσ/Tε的增加，径向位移和环向应力幅值明显减小。

[1] 宫婉婷，丁 敏，徐庆磊，等.地下沼气池池壁土压力取值方法及池盖受力分析[J].农业工程学报,2011,27(4):270-276.

[2] Forrestal M J,Sagartz M J.Radiated pressure in an acoustic medium produced by pulsed cylindrical and spherical shells[J].AMSE Journal of Applied Mechanics,1971(93):1057-1060.

[3] Duffey T A.Transient response of viscoelastic and viscoelastic shells submerged in fluid media[J].AMSE Journal of Applied Mechanics,1976(98):137-143.

[4] Glenn L A,Kidder R E. Blast loading of a spherical container surrounded by an infinite elastic medium[J].Journal of Impact Engineering[J].Engineering Structures,2000(22):984-992.

[5] 张庆元，战人瑞.爆轰荷载作用下球形空腔的动力响应[J].爆炸与冲击,1994,14(2):182-185.

[6] Liu Ganbin,Xie Kanghe.Transient response of a spherical cavity with a partially sealed shell embedded in viscoelastic saturated soil[J].Journal of Zhejiang University Science,2005,6A(3):194-201.

[7] 韩同春,刘干斌.任意荷载下黏弹性饱和土体中球壳的动力响应研究[J].浙江大学学报(工学版),2006,40(5):816-821.

[8] Auslender F,Combescure A.Spherical elastic-plastic structures under internal explosion:Approximate analytical solutions and application[J].Engineering Structures,2000(22):984-992.

[9] 刘林超，杨 骁.分数导数模型描述的饱和土桩纵向振动分析[J].岩土力学,2011,32(2):526-532.

[10] 高华喜,闻敏杰.黏弹性准饱和土中球空腔动力特性[J].力学学报,2012,44(4):112-120.

[11] 刘林超,姚庆钊,闫启方,等.基于积分型分数导数本构方程的黏弹性土层中单桩的竖向复刚度与导纳研究[J].水利学报,2012,43(7):796-802.

[12] 刘林超,闫启方,孙海忠.软土流变特性的模型研究[J].岩土力学,2006,27(sup):214-217.

[13] 何利军,孔令伟,吴文军,等.采用分数阶导数描述软黏土蠕变的模型[J].岩土力学,2011,32(S2):239-244.

[14] Weiland P.Biogas production: current state and perspectives[J].Appl Microbiol Biotechnol,2010(85):849-860.

[15] Timoshenko,S P,Goodier J N.Theory of Elasticity,McGraw-Hill,New York,1977.

[16] Zakout U,Akkas N.Transient response of a cylindrical cavity with and without a bounded shell in infinite elastic medium[J].International Journal of Engineering Science,1997,35(12):1203-1220.

[17] 徐长节,吴世明.饱和土中球面波的传播[J].应用数学和力学学报,1998,19(3):223-231.

[18] 徐长节,蔡袁强.粘弹性饱和土中球空腔的动力响应[J].土木工程学报,2001,34(4):88-92.

Dynamic characteristics of a deeply embedded spherical biogas digester in viscoelastic soil★

Qian Changgen Xiang Tianyong Wen Minjie*

(JiaxingVocationalTechnicalCollege，Jiaxing314036，China)

Using the analytical method, harmonic vibration characteristics of a deeply embedded spherical biogas digester in viscoelastic soil subject to the cyclic loading are investigated in frequency domain. The die structure is treated as homogeneous elastic medium and shell structure, respectively. Based on the theory of elastic and Flügge, the analytical solutions for dynamic responses of the spherical biogas digester in fractional derivative viscoelastic soil are derived. By the continuity conditions at the boundary, the expressions of undetermined coefficients are determined. On the basis, the comparative analysis of system dynamic response with homogeneous elastic medium and shell structure is derived. The influences of the parameters of fractional derivative, soil and die on the system dynamic response are analyzed. It is shown that the dynamic responses of die structure under two models have significant difference.

biogas engineering, viscoelastic soil, spherical biogas digester, harmonic vibration, analytical solutions

1009-6825(2017)18-0041-04

2017-04-18★：浙江省重点科技创新团队项目(2013TD12)；国家国际科技合作专项项目(2014DFE90040)

钱长根(1966- )，男，硕士，副教授； 向天勇(1971- )，男，博士，副教授

闻敏杰(1986- )，男，博士生

TU411.8

A