基于改进Basin-Hopping Monte Carlo算法的Fen-Ptm(56 n+m 6 24)合金团簇结构优化∗

刘暾东 李泽鹏 季清爽 邵桂芳 范天娥 文玉华

1)(厦门大学自动化系,厦门 361005)

2)(厦门大学物理学系,厦门 361005)

基于改进Basin-Hopping Monte Carlo算法的Fen-Ptm(56n+m6 24)合金团簇结构优化∗

刘暾东1)李泽鹏1)季清爽1)邵桂芳1)†范天娥1)文玉华2)

1)(厦门大学自动化系,厦门 361005)

2)(厦门大学物理学系,厦门 361005)

(2016年9月4日收到;2016年12月8日收到修改稿)

合金纳米团簇可以充分利用多种金属的协同效应来实现材料的多功能特性,因而备受关注.本文利用改进的Basin-Hopping Monte Carlo算法研究了不同尺寸和不同比例下的Fe-Pt二元合金团簇的结构稳定性.为证明初始结构相关性,引入了相似函数来分析合金团簇稳定结构与其对应的单金属团簇结构之间的相似性,并分析了Fe-Pt合金团簇在稳定结构下的元素分布.研究结果表明:对于N6 24的Fe-Pt合金团簇,其结构并没有随原子数的增长呈现出明显的形状变化.但是就原子分布而言,对于相同尺寸下不同比例的原子结构,Fe元素趋向于分布在外层,而Pt元素更趋向于分布在内层;对于相同比例不同尺寸的原子结构也得到了同样的结论,并且在Fe原子比例越大的情况下,这种趋向的分布越明显.此外,通过计算合金团簇与单一金属团簇的结构相似函数,发现N6 24的Fe-Pt合金团簇在吸收Fe单金属和Pt单金属基态结构的基础上,随着元素比例的变化,发生了不同于单金属基态结构的变化,并且不同比例结构差异较大.最后,通过计算Fe-Pt合金团簇能量的二阶有限差分值,在Fe-Pt表现出分离结构状态时找到了相对稳定度最好的稳定结构.

合金团簇,Basin-Hopping Monte Carlo,稳定结构,原子分布

1 引 言

二元合金纳米团簇可以充分利用两种金属之间的电子结构与晶体结构的协同效应来实现材料的双功能特性,因而在化学和物理方面表现出优于单金属团簇的性质,在催化、生物医学、新材料等领域具有广泛的应用[1,2].此外,合金团簇的物理和化学性质可通过改变元素的比例、结构有序度和团簇尺寸来调控,因而成了目前实验和理论研究的热点,其光学、磁学和催化性质得到了广泛的研究.在金属团簇中,铁(Fe)团簇作为过渡金属,不仅具有磁性,而且与其他贵金属团簇一样,具有高反应性和催化活性,因此在信息存储、能源化工和生物医学等领域中具有广阔的应用前景.铁与铂(Pt)、钯(Pd)和金(Au)等贵金属结合形成二元或多元合金,不仅可以显著提高铁团簇的催化活性,还能实现团簇的多功能特性[3,4].因此,本文将以Fe-Pt合金纳米团簇作为研究对象,探讨其原子比例、原子有序化和团簇尺寸对结构稳定性的影响.

团簇的结构决定了它们的物理或化学性质,因此研究合金纳米团簇的稳定结构是研究合金团簇其他性质的基础[5,6].另外,团簇的结构依赖于团簇尺寸、原子比例和原子有序化分布,因此可以通过改变团簇的这些特征来改变团簇的物理与化学性质.合金团簇的表面结构和原子偏聚程度同样决定着其化学活性.因此研究Fe-Pt合金团簇的稳定结构,分析不同原子比例对原子分布现象以及表面偏聚程度的影响,以及原子数对团簇结构的影响,对了解Fe-Pt合金团簇的物理和化学性质具有重要的意义.

目前,对于合金团簇结构稳定性研究,最常用的方法是基于密度泛函理论的计算方法和基于原子间经验势函数的全局优化算法.基于密度泛函理论的计算方法计算精度高,但对于原子数较多且存在大量同分异构体的合金团簇的结构研究,计算量相当大,难以获得团簇结构与其尺寸、元素比例的依赖关系.而利用经验势函数来描述原子间相互作用,将合金团簇结构稳定性的研究转换成一个全局最优化问题,使得如蒙特卡洛罗算法[7]、盆地跳变算法[8−12]、模拟退火算法[13]、遗传算法[14−16]、动态晶格法[17]等可以用来研究团簇的结构优化.例如:Wales和Doye[10]较早利用盆地跳算法结合蒙特卡罗算法进行单金属团簇结构研究;Rondina等[12]针对盆地跳变蒙特卡罗算法(Basin-Hopping Monte Carlo,BHMC)的不足之处做了大量改进,并计算了单金属团簇和较为稳定的二十面体结构上的合金团簇稳定结构.然而,随着原子数的增长,势能面上的局部最小值也呈指数增长,并且二元合金团簇将会出现大量的同分异构体,因此,探索一种有效的全局优化算法对于合金团簇结构优化十分重要.本文在采用Gupta经验势能来描述原子间相互作用力的基础上,提出了一种改进BHMC算法来有效地优化Fe-Pt合金团簇的结构.在现有的BHMC的基础上,引入了更优的初始化方式和局部优化算子,并结合遗传算法,对种群中能量较低的个体首先进行位置结构的相对固定,然后再利用遗传局部优化来寻找原子类型的最优分布,这样让求解合金团簇最优同分异构体的问题变得更加有效;同时考虑了不同尺寸和不同原子比例对团簇稳定结构的影响,分析了团簇表面原子偏聚和原子有序化等结构特征.

2 研究方法

2.1 原子间的相互作用势

纳米团簇中原子间的相互作用通常采用经验势函数来描述,研究Fe-Pt合金团簇稳定结构的实质就是寻找势能面上的能量最小值.能量越低的团簇,其结构越稳定.本文采用Gupta势能来描述Fe-Pt合金团簇中原子间的相互作用[14,15,18−22].这种描述金属键的势函数是基于紧束缚势的二阶矩近似,诸多研究已证明了它能有效地描述过渡金属元素及其合金的热动力学和输运性质[18].Gupta多体相互作用势主要由Born-Mayer排斥项Vr(i)和含多体效应的吸引项Vm(i)组成,后者取自紧束缚模型电子态密度的二次矩近似[14,22].对于原子总数为N的团簇,其总的势能Vn可描述为:

其中rij表示原子i与原子j间的距离,表示两类原子间的特征长度,一般以块体材料的第一近邻距离表示;Aij是衡量原子间的排斥强度的量;ξij是有效跳跃积分,通常与原子类别有关;pij是反映排斥作用随原子间约化距离指数递变趋势的量;qij是有效跳跃积分与相对原子间距之间关系的量.这些参数通常可通过拟合金属的性质得到,例如内聚能、晶格参数和弹性常数.Gupta势函数下Fe和Pt金属的参数[22]如表1所列.

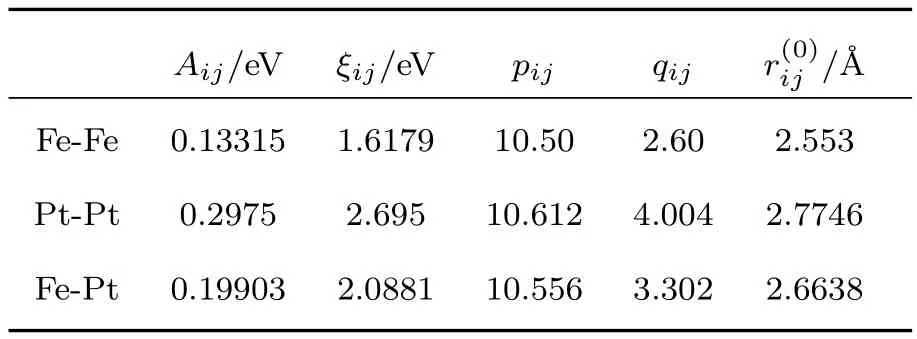
表1 Fe,Pt和Fe-Pt合金的参数Table 1.The parameters of Fe,Pt,and their alloy.

2.2 现有的BHMC算法

传统的BHMC算法本质是将局部极小化方法和蒙特卡罗方法相结合.包括如下流程:1)随机初始化种群构型,并对初始种群做局部极小化处理,得到局部最优;2)利用随机扰动产生新的构型,并对新的构型使用局部极小化方法,得到新的局部最优;3)比较前后两次的局部最优结果,判断是否接受新构型;4)进行反复迭代计算,直到搜索到全局最优构型.在该方法中,通过使用局部极小化方法可以将团簇结构的势能函数面由曲面转换成阶梯状,然后利用蒙特卡罗方法搜索全局最优值[10,11].局部极小化方法极大地缩小了蒙特卡罗方法的搜索空间,提高了BHMC算法的整体优化效率.但是使用随机扰动,会降低搜索效率,且每次扰动的变化小,跳不过较高的势能壁垒,容易陷入局部最优.

为避免陷入局部最优,相关研究人员[12,23]提出了多种跳出局部的扰动策略,如球切扰动、面切扰动、随机交换扰动、原子移位扰动和辅助过滤扰动等.这样就能很好地求解团簇问题中的结构优化问题.我们借鉴引入了其中两种扰动方式:一种是原子移位扰动,即对原子坐标进行随机的位移,得到新的原子坐标位置的结构,从而产生新的团簇结构;另一种是球切扰动,即对已知的父代和母代两个团簇个体进行球域范围内外的交叉组合,从而得到新的子代团簇结构,其示意图如图1.前者通过小扰动可以实现局部寻优,后者通过增加大的扰动可以帮助跳出小的局部最优,利用这两种扰动方式进行团簇结构更新,不断搜索新的团簇结构,达到团簇结构寻优的目的.

此外,我们发现初始结构对利用现有的BHMC算法有一定影响.我们进行实验分析,分别得到基于Fe单金属、Pt单金属和原子数目较小的Fe-Pt合金团簇的初始最稳定结构.以N=13为例,图2给出了Fe原子与Pt原子各种比例情况下的初始最优结构.

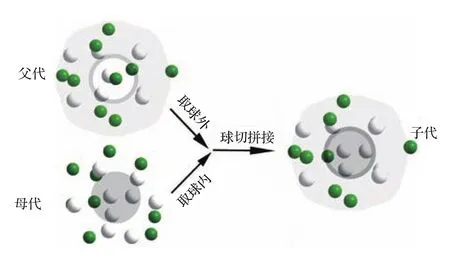
图1 (网刊彩色)球切扰动示意图Fig.1.(color online)The schematic of sphere-cutsplice.

由图2可以发现,对于FenPt13-n,无论是单金属还是合金的最优结构,都十分类似.我们比较了其他原子数较小的单金属结构和合金团簇稳定结构,也得到了类似的结论.这说明在单金属最优结构的基础上再进行合金结构优化是合理的,并能保证获得比随机初始化更优的结构.

图2 (网刊彩色)N=13时,FenPtm所有比例的最低能量构型 绿色表示Fe原子,白色表示Pt原子,n表示Fe原子数,m表示Pt原子数Fig.2.(color online)The lowest-energy configurations of Fe-Pt alloy clusters for different compositions with N=13.Fe atoms are in green,Pt atoms in white,n represents the number of Fe atoms and m represents the number of Pt atoms.

2.3 改进的BHMC算法

为研究Fe-Pt合金团簇的结构稳定性和结构特征,首先需要计算基于势能函数((1)式)的能量最小值,从而获得最稳定的几何结构.寻找势能最小值是一个全局优化问题,而合金团簇的结构寻优问题可以理解为结构优化和元素原子排布优化的组合优化问题,因此求解该问题的算法必须同时具备较好的结构优化特性和元素排布优化特征两个方面的能力[14,24−26].如图3所示,结构优化是指获取某个原子数下合金团簇能量值最低的结构(图3(a)),元素排布优化是指在某个结构下,获得合金元素在该结构内不同位置上分布的能量值最低的结构(图3(b)).由于在所有随机优化算法中,算法的收敛速度和搜索能力在很大程度上取决于在当前解的基础上探索新解的策略.为此本文提出了一种新的改进BHMC算法,在现有的改进算法的基础上,引入了遗传局部优化,以增加算法对二元合金原子元素排布优化的能力.

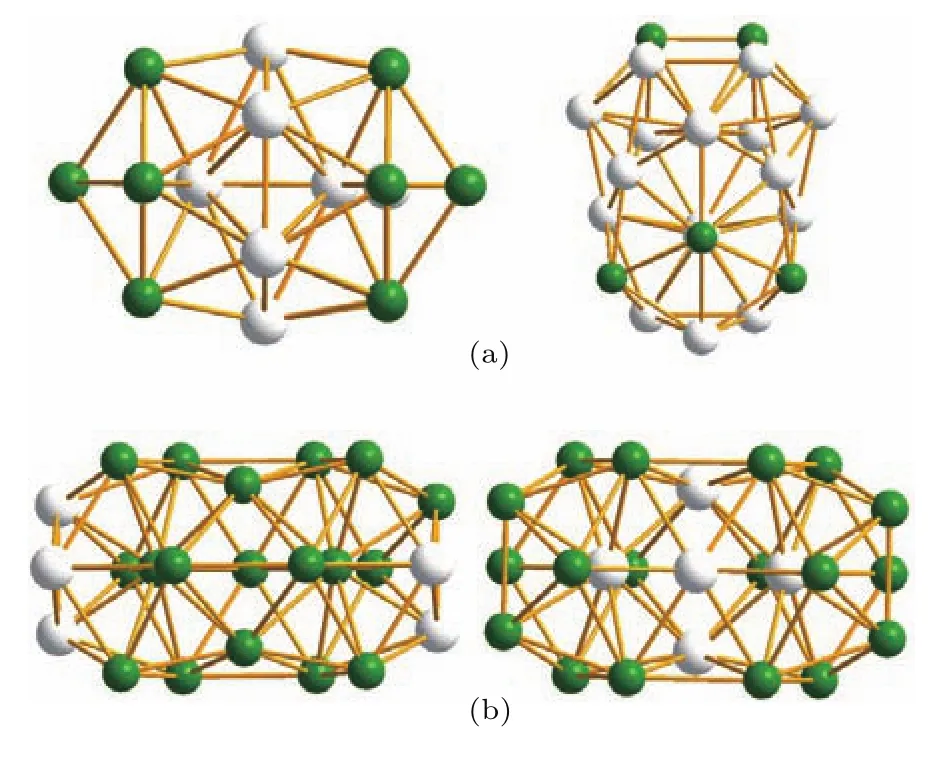
图3 (网刊彩色)合金团簇结构寻优的组合优化示意图(a)结构优化;(b)元素排布优化Fig.3.(color online)The combinatorial optimization schematic of alloy cluster structure:(a)Structured optimization;(b)element configuration optimization.

寻找原子总数为N的FenPtm二元合金团簇稳定结构,改进BHMC算法主要包括如下步骤:1)初始化种群,得到原子总数为N的合金团簇在各种不同比例情况下的初始结构;2)对初始化的结构进行局部优化,得到初始化后的局部最优结构;3)对每个局部最优结构的每个原子进行扰动处理,并计算扰动后个体的能量,保存能量更低的结构;4)对能量更低的结构进行遗传局部优化处理,得到当前最优结构的元素最优排布;5)不断重复扰动算子操作和当前最优结构下的遗传局部优化,直到搜索到最终的最优结构.改进的BHMC算法优化FenPtm合金团簇的流程如图4所示.

图4 改进的BHMC算法流程图Fig.4.The flowchart of the improved BHMC algorithm.

2.3.1 初始化

结合图2的实验结论,应用改进的BHMC算法进行FenPtm合金团簇能量优化,我们设计了两个初始化的过程:一是种群的初始化,得到整个算法流程的初始种群;二是遗传局部种群的初始化,得到较好结构下的随机元素排布的初始种群.

1)种群初始化:对于某个合金结构,通过在连续空间里初始原子的配置,即在随机的球形容器{R}内,找到N个原子粒子的基态构型{R}=r1,r2,r3,···,rN,其中

Rc=是元素α对应的共价半径[12],种群的大小会随着原子个数发生变化.在改进算法中,通过引入相同原子个数的Fe和Pt单金属的最稳定结构作为初始构型,从而避免完全随机方式无法产生所需的初始稳定结构,并获得较优的个体.

2)遗传局部种群初始化:对原子总数为N的FenPtm二元合金团簇,在结合扰动算子得到较好结构的基础上,对原子位置进行相对固定,通过改变原子种类随机生成一个个体P,个体P的表示方式如下:

其中,每个pi的取值为0或者1,分别代表Fe原子或Pt原子,i表示第i个原子.pi的取值还必须满足一个条件:

2.3.2 遗传局部优化

合金团簇的结构优化比单金属团簇要复杂得多.在应用扰动算子时,不但要保证团簇的总原子数不变,还要保证团簇中每种元素的原子个数不变.此外,即使它们的几何构型极其相近,只要两种原子的位置不同,就可产生出多种不同能量的团簇结构.特别是在两种合金原子数越接近1:1比例的情况下,这样的团簇就越多,这大大增加了寻找稳态结构的难度[14,24−26].对于原子总数为N的合金团簇FenPtm的单个同分异构体而言,其homotops异构构型[24−26]的个数是

例如,就Fe10Pt10而言,它存在184756个homotops异构构型.

在基本的BHMC算法中,通常采用表面削弱和结构重组等扰动算子,以增强其跳出局部最优的能力.但这种扰动力度很小,很难保证在存在大量同分异构体的情况下跳出局部最优.为解决此类问题,我们在已有的BHMC算法基础上引入了遗传局部优化算子,以在较短的时间范围内找到每单个同分异构体的最优的homotops异构构型,从而大大节约在最优homotops异构构型上的求解时间.

遗传局部优化的具体操作如下:1)对经过扰动算子处理后得到的良好个体,进行位置相对固定;2)利用2.3.1节的遗传局部种群初始化方法产生初始种群;3)利用遗传算法,分别对原子元素的分布进行交叉、变异和选择操作[14,15],以实现相对寻优;4)通过不断的迭代找到相对固定原子位置下的最优同构构型;5)每次遗传局部寻优结束后,进行最速下降局部优化处理.

3 实验结果与分析

3.1 Fe-Pt合金团簇的稳定结构

基于本文提出的改进BHMC算法,我们对N6 24的FenPtm合金团簇进行了结构寻优,图5给出了N=24时不同比例情况下的Fe-Pt合金团簇稳定结构优化结果.

如图5所示的FenPtm各种比例情况下合金团簇的稳定结构,可以看出合金团簇的稳定结构具有较好的对称性.同时,部分不同原子比例合金团簇之间有很强的结构相似性,如Fe5Pt19与Fe12Pt12.但也有部分不同比例合金团簇之间结构相似性较差,如Fe19Pt5与Fe12Pt12.由于采用了单金属团簇结构作为实验初始结构,为验证合金实验结果与初始结构的相关性,本文引入了相似函数S[14,25,26]以量化合金团簇与单金属团簇之间的差异,并更好地分辨相同尺寸下不同比例混合团簇间的差异性.相似函数S的表达式为:

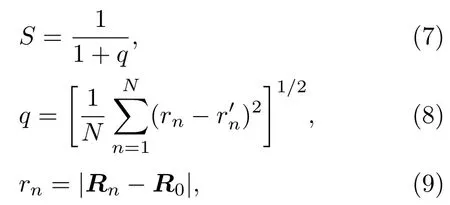
式中R0是该团簇的几何中心,rn是合金团簇中第n个原子到其几何中心的距离,r′n是第n个原子所属单质团簇中相应原子到其几何中心的距离.S值越接近于1,表明该合金团簇与对应的单金属团簇的基态结构越相似;反之则越不相似.图6给出了FenPt24−n(n=0—23)混合团簇稳定结构分别与单金属团簇Fe24和Pt24比较得到的相似函数S曲线.

由图6可见,S值在0.7—0.95之间变化.比较图6与图5,我们发现在Fe原子数为3,14,18和20时,其结构与邻近的其他Fe原子数的FenPt24−n合金团簇具有较大的结构差异.这说明FenPt24−n合金团簇在吸收Fe24和Pt24单金属团簇基态结构的基础之上,发生了结合自身比例变化的畸变.正是由于这些畸变,使得FenPt24−n合金团簇呈现如图6所示的5种不同的结构形态.为了进一步探究Fe-Pt合金团簇的稳定结构形态,我们利用寻优得到的N<24时Fe,Pt单金属原子团簇最低能量结构,计算得到了相对能量较低的单金属幻数结构,分别是Pt13,Pt22,Fe13,Fe19及Fe23.这些结构可以分成三种情况:N=13时,两种单金属团簇都具有比较高的相对稳定度;N=22时,Pt单金属原子团簇的相对稳定度较好,而Fe较差;N=19和23时,则与第二种情况相反.为此,我们选取了N=13,22和23三种具有代表性的情况,来分析单金属结构相对稳定时合金团簇的结构变化情况,并得到如图7所示的相似函数曲线.

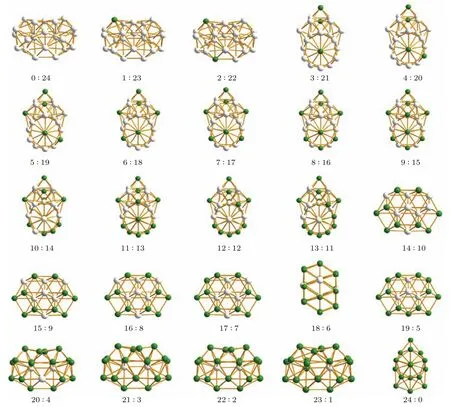
图5 (网刊彩色)N=24时,FenPtm所有比例的最低能量构型,绿色表示Fe原子,白色表示Pt原子,其中n:m,n表示Fe原子数,m表示Pt原子数Fig.5.(color online)The lowest energy configurations of FenPtmfor different compositions with N=24,Fe atoms are in green,Pt atoms in white.For the composition n:m,n represents the number of Fe atoms,and m represents that of Pt atoms.

图6 (网刊彩色)N=24合金团簇的稳定结构随Fe原子数增加相似函数S的变化曲线Fig.6.(color online)The similarity function curves of the stable structures of alloy clusters with the increase of Fe atoms for N=24.

图7 (网刊彩色)合金团簇稳定结构的相似函数S随Fe原子数增加时的变化曲线 (a)N=13;(b)N=22;(c)N=23Fig.7.(color online)The similarity function curves of the stable structures of alloy clusters with the increase of Fe atoms for(a)N=13,(b)N=22 and(c)N=23.

由图7相似函数曲线图可以发现:N=13时,S的值在0.88—1之间,说明FenPt13−n合金团簇的稳定结构与Fe13和Pt13单金属基态结构相似,这与图2的稳定结构是一致的,即FenPt13−n各种比例下的合金团簇结构十分类似;N=22时,S的值在0.75—1之间,主要在n=6和21时相似函数曲线有起伏变化,FenPt22−n合金稳定结构随Fe原子数的变化呈现出如图7(b)所示的两种不同结构形态,n=1—6和n=21时所获得的合金稳定结构类似,而n=7—20时合金的稳定结构类似,这说明FenPt22−n合金团簇稳定结构在发生了结合自身比例变化的畸变;N=23时,S的值在0.7—1之间,主要在n=18和19时相似函数曲线有起伏变化,FenPt23−n合金稳定结构随Fe原子数的变化呈现出如图7(c)所示的两种不同结构形态,并且n=1—17和n=20时合金的稳定结构类似,而n=18—19和n=21—22时合金的稳定结构类似,说明FenPt23−n合金团簇稳定结构也发生了结合自身比例变化的畸变,以达到自身的结构稳定.

此外,一些比较特殊的原子比例情况下得到的合金团簇可能会跟单金属团簇的稳定结构差异较大. 导致这些差异的主要原因是Fe-Fe,Fe-Pt和Pt-Pt的原子键键长不同.由于导致成键后形成的稳定结构产生差异[14,25],使得在比较特殊的比例之下,Fe-Pt合金形成的稳定结构与单金属基态结构相差较大.

3.2 偏聚分析

为进一步分析某个FenPtm合金团簇稳定结构下的原子分布情况,我们引入了不同类型原子与其结构几何中心的平均距离大小来定量描述不同原子沿着团簇径向的偏聚.

其中,Ra表示a类型原子与几何中心的平均距离,na是a类型原子的总数,ri表示在结构中已保存的第i个a类型原子距离其几何中心的距离.

利用(10)式,我们得到了不同尺寸、不同比例下FenPtm合金团簇的各类原子离其几何中心的距离,如图8所示.通常来说,几何中心间距差别越大表明两种原子越处于分离状态,反之趋于混合状态.

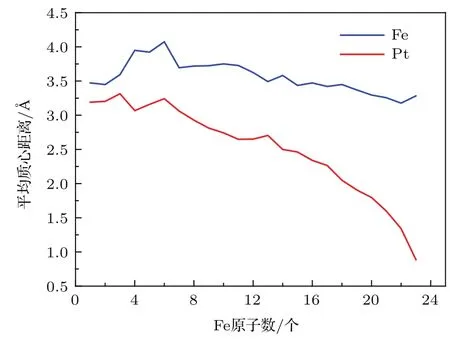
图8 (网刊彩色)N=24时合金团簇随Fe原子数增加的Fe,Pt平均几何中心距离曲线Fig.8.(color online)The distance of centers of Fe and Pt mass with the increase of Fe atoms for alloy cluster with N=24.

由图8中Fe-Pt二元合金团簇原子距其几何中心的平均距离曲线可以看出,在不同原子比例情况下,Fe原子的平均距离都比Pt的平均距离要大,这说明Fe原子倾向于分布在Fe-Pt合金团簇的外层,而Pt原子则偏向于分布在Fe-Pt合金团簇的内层.这是由于Fe的表面能比Pt的要低,当具有较低表面能的Fe分布在Fe-Pt合金团簇的表面时,可以显著地降低该团簇的表面能,从而降低团簇的总能.随着Fe原子个数的增加,对于不同比例的Fe-Pt合金团簇来说,Fe原子的平均几何中心距离变化较小,在较为稳定的范围内波动,而Pt原子的平均几何中心距离则呈现逐渐减小的趋势,说明Fe原子占比越大的情况下,Fe原子偏向分布在合金外层,而Pt原子偏向分布在合金内层的趋势会更加明显.

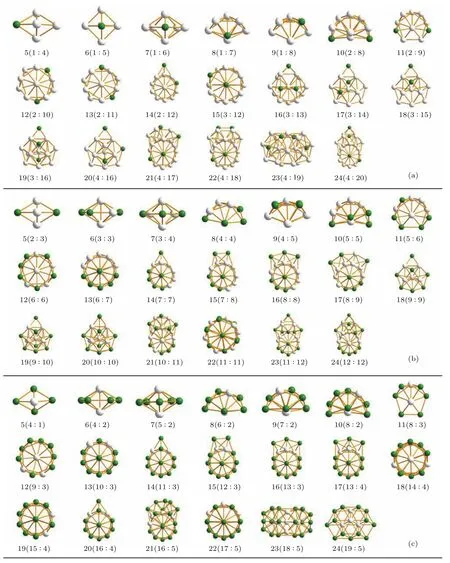
图9 (网刊彩色)原子总数N=5—24,在比例为(a)2:8,(b)5:5和(c)8:2时Fe-Pt合金团簇的最低能量构型.绿色表示Fe原子,白色表示Pt原子,其中N(n:m),N表示总原子数,n表示Fe原子数,m表示Pt原子数Fig.9.(color online)The lowest energy configurations of Fe-Pt alloy clusters with different sizes N=5–24 and three atomic ratios of(a)2:8,(b)5:5 and(c)8:2.Fe atoms are in green,Pt atoms in white.For N(n:m),N represents the total number of atoms,n represents the number of Fe atoms and m represents Pt atoms.

3.3 不同尺寸合金团簇的结构稳定性比较

为进一步描述合金团簇在不同尺寸下的结构稳定性,我们对Fe-Pt合金在2:8,5:5和8:2比例情况下的原子总数为N=5—24的稳定结构进行了分析,如图9所示.

由图9可以看出,Fe-Pt合金团簇稳定结构随总原子个数N的增加而呈现出结合成环的趋势,特别是在总原子数为N=13时首次形成类二十面体的稳定结构[15].此外,在Fe原子个数占优的情况下,Fe-Pt合金团簇更容易成环,形成对称性更高的结构.这是因为在Fe原子数较多时,Pt原子会更加接近合金团簇稳定结构的几何中心(如图8所示),这样更加有益于形成稳定结构.

同时,为了能更好地比较各种原子比例下Fe-Pt合金团簇的差异性,我们引入了二阶差分能∆2E(n,m)[14,25],

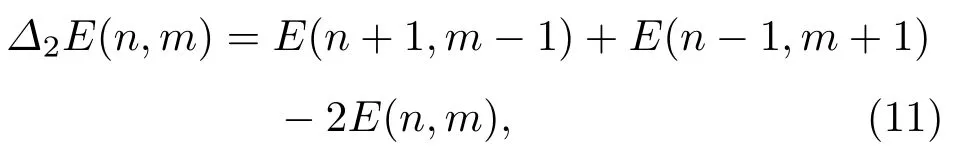
其中E(n+1,m−1),E(n,m)和E(n−1,m+1)分别表示Fen+1Ptm−1,FenPtm和Fen−1Ptm+1的最低能量.利用(11)式,我们可以得到不同尺寸、不同比例情况下合金团簇的二阶差分能,如图10所示.二阶差分能值越大,说明此时的合金结构相对于邻近团簇越稳定,反之则越不稳定.

如图10所示,4种情况下的二阶差分能曲线都呈波浪式变化. 其中得到Fe12Pt1,Fe20Pt2,Fe21Pt2和Fe22Pt2是各个情况下的峰值,分别具有对应情况下的最高稳定性.图11给出了二阶差分能最大的几个Fe-Pt合金团簇稳定结构.

由图11可以看到:对于Fe12Pt1,Fe20Pt2,Fe21Pt2和Fe22Pt2而言,在Pt原子位于合金团簇稳定结构的内层,Fe原子位于稳定结构外层,并且内外层原子呈现比较明显的分离情况时,合金团簇结构将会更稳定.

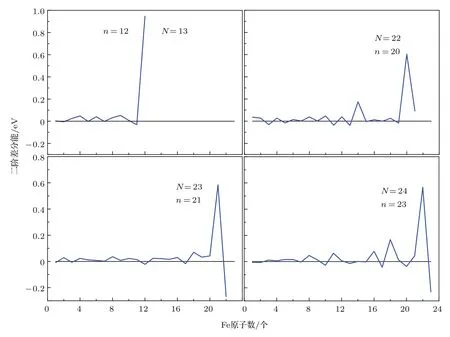
图10 (网刊彩色)N=13,22,23和24时Fe-Pt合金稳定结构的二阶差分能Fig.10.(color online)The second energy difference for the Fe-Pt alloy clusters with N=13,22,23 and 24,respectively.

图11 (网刊彩色)N=13,22,23和24时二阶差分能最大的原子比例下的合金稳定结构 绿色表示Fe原子,白色表示Pt原子,其中N(n:m),N表示总原子数、n表示Fe原子数,m表示Pt原子数Fig.11.(color online)The stable structures of Fe-Pt alloy clusters for the composition which the largest of the second energy difference is largest when N=13,22,23 and 24 respectively.Fe atoms are in green,Pt atoms in white.For N(n:m),N represents the total number of atoms,n represents the number of Fe atoms and m represents that of Pt atoms.

4 结 论

本文采用改进的BHMC算法结合Gupta多体势对5—24个原子、各种比例情况下的Fe-Pt合金团簇进行了研究.为提高算法搜索性能,本文引入了单金属稳定结构初始化和遗传局部优化对现有的BHMC算法进行改进.通过对各种比例下的稳定结构分析,我们发现Fe原子倾向于分布在混合团簇的外表层,而Pt原子主要分布在内层.其次,合金团簇的相似函数分析表明Fe-Pt合金团簇稳定结构随着原子的比例改变而呈现明显的变化.此外,合金团簇的二阶差分能分析表明在Fe,Pt呈现完全分离状况时,Fe-Pt合金团簇具有更好的稳定性,其中Fe12Pt1,Fe20Pt2,Fe21Pt2和Fe22Pt2是幻数结构团簇.我们的研究证实:改进的BHMC算法作为一种全局优化算法,能够用来处理合金团簇的稳定结构寻优问题,并得到较好的结果.

[1]Baletto F,Ferrando R 2005Rev.Mod.Phys.77 371

[2]Balamurugan B,Maruyama T 2005Appl.Phys.Lett.87 143105

[3]Koenigsmann C,Santulli A C,Gong K,Vukmirovic M B,Zhou W,Sutter E,Wong S S,Adzic R R 2011J.Am.Chem.Soc.133 9783

[4]Soares A V H,Perez G,Passos F B 2016Appl.Catal.B185 77

[5]Xiao S,Hu W,Luo W,Wu Y,Li X,Deng H 2006Eur.Phys.J.54 479

[6]Liu T D,Fan T E,Zheng J W,Shao G F,Sun Q,Wen Y H 2016J.Nanopart.Res.77 2

[7]Cheng D J,Huang S P,Wang W C 2006Chem.Phys.330 423

[8]Kim H G,Choi S K,Lee H M 2008J.Chem.Phys.128 144702

[9]Zhan L,Piwowar B,Liu W K,Hsu P J,Lai S K,Chen J Z 2004J.Chem.Phys.120 5536

[10]Wales D J,Doye J P K 1997J.Phys.Chem.A101 5111

[11]Cheng L,Feng Y,Yang J,Yang J 2009J.Chem.Phys.130 214112

[12]Rondina G G,Da Silva J L F 2013J.Chem.Inf.Model.53 2282

[13]Ruette F,González C 2002Chem.Phys.Lett.359 428

[14]E X L,Duan H M 2010Acta Phys.Sin.59 5672(in Chinese)[鄂箫亮,段海明 2010物理学报 59 5672]

[15]Liu L,E X L,Duan H M 2011J.At.Mol.Phys.28 459(in Chinese)[刘莉,鄂箫亮,段海明 2011原子与分子物理学报28 459]

[16]Ren L,Cheng L,Feng Y,Wang X 2012J.Chem.Phys.137 014309

[17]Shao X,Cheng L,Cai W 2004J.Comput.Chem.25 1693

[18]Cleri F,Rosato V 1993Phys.Rev.B48 22

[19]Darby S,Mortimer-Jones T V,Johnston R L,Roberts C 2002J.Chem.Phys.116 1536

[20]Chen Z,Jiang X,Li J,Li S,Wang L 2013J.Comput.Chem.34 1046

[21]Varas A,Aguilera-Granja F,Rogan J,Kiwi M 2015J.Magn.Magn.Mater.394 325

[22]Huang R,Wen Y H,Shao G F,Sun S G 2016Phys.Chem.Chem.Phys.18 1701

[23]Chen Z,Jiang X,Li J,Li S 2013J.Phys.Chem.138 214303

[24]Rossi G,Ferrando R 2009J.Phys.Condens.Matter21 084208

[25]Hristova E,Dong Y,Grigoryan V G,Springborg M 2008J.Phys.Chem.A112 7905

[26]Hristova E,Grigoryan V G,Springborg M 2008J.Chem.Phys.128 244513

PACS:36.40.–c,31.15.B–,61.82.Bg DOI:10.7498/aps.66.053601

Structural optimization of Fen-Ptm(5 6n+m6 24)alloy clusters based on an improved Basin-Hopping Monte Carlo algorithm∗

Liu Tun-Dong1)Li Ze-Peng1)Ji Qing-Shuang1)Shao Gui-Fang1)†Fan Tian-E1)Wen Yu-Hua2)

1)(Department of Automation,Xiamen University,Xiamen 361005,China)
2)(Department of Physics,Xiamen University,Xiamen 361005,China)

4 September 2016;revised manuscript

8 December 2016)

Alloy nanoclusters have received extensive attention because they can achieve bifunctional properties by making good use of the cooperative effect of two metals.In this paper,an improved Basin-Hopping Monte Carlo(BHMC)algorithm is proposed to investigate the structural stabilities of Fe-Pt alloy nanoclusters.Different cluster sizes and chemical compositions are considered.Moreover,a similarity function is introduced to analyze the structural similarity between the stable structures of alloy clusters and those of their monometallic clusters.Meanwhile,the atomic distributions of Fe-Pt alloy clusters are considered for their stable structures.The results indicate that for Fe-Pt alloy clusters with the sizeN6 24,there is no significant structural evolution with the increase of cluster size.Fe atoms prefer to segregate at the peripheral positions of the clusters,while Pt atoms tend to occupy the interior.The same distribution result can be obtained for the structures of clusters with different compositions.With Fe composition increasing,this distribution trend is more pronounced for the Fe-Pt alloy clusters.

In addition,by calculating the structural similarity function between alloy and monometallic clusters,we find that the stable structures of Fe-Pt alloy clusters gradually vary with composition ratio.Moreover,when the Fe atoms or Pt atoms are added into the Fe-Pt alloy system,they change the stable structures of Fe-Pt alloy clusters,resulting in a different structure from Fe and Pt monometallic ones.Also,the structural similarity is different when the Fe composition varies.Furthermore,the best stable structures of Fe-Pt clusters with different compositions and sizes are obtained by calculating the second-order finite difference in energy of Fe-Pt alloy clusters.

alloy clusters,Basin-Hopping Monte Carlo,stable structures,atomic distribution

PACS:36.40.–c,31.15.B–,61.82.Bg

10.7498/aps.66.053601

∗国家自然科学基金(批准号:11474234,51271156,61403318)和中央高校基本科研业务费(批准号:20720160085)资助的课题.

†通信作者.E-mail:gfshao@xmu.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.11474234,51271156,61403318)and the Fundamental Research Fund for the Central Universities,China(Grant No.20720160085).

†Corresponding author.E-mail:gfshao@xmu.edu.cn