粉料堆积密度与堆积深度关系研究及应用

何富君 ，樊 华，陈 兴, 刘宏源

(东北石油大学机械科学与工程学院，黑龙江 大庆 168318)



粉料堆积密度与堆积深度关系研究及应用

何富君 ，樊 华，陈 兴, 刘宏源

(东北石油大学机械科学与工程学院，黑龙江 大庆 168318)

为了提高粉料包装机械这类机械系统的计量精度，从理论上研究了粉料堆积密度与堆积深度的关系，改进了自然堆积密度试验的测量方法，并对压实密度与压实应力经验公式进行优化。采用等质量分层法，建立物料堆积密度与堆积深度关系的数学模型。在修正多种物料自然堆积密度测量数据的基础上，重新拟合了相关公式。以小麦粉为例，建立了小麦粉的堆积深度与堆积密度的关系式。针对螺旋下料工程应用，提出了一种新的计量方法。

粉料；堆积密度；压实密度；堆积深度；粉料计量

一直以来，在工、农业的粉料计量中，利用物料体积来估算物料质量的方法(本文称作体积计量法)得到了广泛应用，体积计量法是基于物料的堆积密度为一个定值的假设情况下应用的。伴随着粉料的储存、运输、加工等行业的进一步发展，人们在实际应用中发现，粉料的堆积密度并非固定不变的，而是与物料的堆积深度有着密切的关系。对于应用在估算一些像大型仓储容器的储存能力或者对于像粉料包装机这类计量精度要求高、物料输出量变化大的设备计量中，应用体积计量法时则会产生较大的误差。对此，许多学者在这一领域进行了积极的研究和探索[4-6]。

谭生禄等曾提出料仓出料口处的物料受自身压力的影响，其堆积密度会大于进料口处的堆积密度，从而对填充率的计算产生较大影响[1]。他们提出的解决方案是采用二级料仓来减少进料口处的压力变化，从而保证了填充率的稳定。但是他们并没有从理论上阐述采用二级料仓是如何减少出料口的压力变化的。

冈小天等人最早提出了物料堆积密度与堆积深度之间存在一定联系的理论，在物料的应力计算模型中引进了径向分布应力，并推导出了一般性的密度分布公式[2]。但是公式中参数众多，计算复杂，而且需要确定产生不连续的边界条件，给实际计算带来了很大难度。

廖荣福等设计了测量粉料压实力与堆积密度关系的实验装置[3,4]。田经烨等进一步通过对几种物料的压力试验得出了压实力与堆积密度的关系曲线,并拟合出了相应物料的计算公式，得出物料的堆积密度随着堆积高度的增加而增大，但堆积密度增加率逐渐减小的结论[5]。他们用试验的方法为粉料计量领域提供了一个新思路。

为了从理论上探究物料的堆积密度变化规律及粉料的计量原理，我们开展了压实应力与堆积深度关系的研究，以期能够为粉料容积的准确计量提供理论指导。

1 数学模型的建立

文献[5]中提出物料的堆积密度随堆积深度发生变化，因此本研究建立了等质量分层计算模型。把目标物料设为直径为D、总高度为H的圆柱型的粉料，由n层质量相同物料堆砌而成，由上至下设层数为第1层、第2层、…、第n层，如图1所示。设每层物料的质量为m,则物料总质量:

m总=n·m

(1)

图1 物料分层示意图

每层物料产生的压实应力σb为：

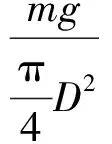
(2)

第i层物料所承受的压实应力σi为前(i-1)层物料所产生的压应力，即：

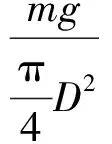
(3)

设各层的堆积密度(单层物料的平均堆积密度的简称)为ρi,设每层的物料厚度为hi,则有：

(4)

因此，只需要知道每层的厚度hi，就可根据公式(4)及总高度H求得每层的堆积密度ρi及物料的层数n，再根据公式(1)就可以求得物料总质量m总。

由于每一层物料的质量相同，这样各层的物料就可以看作是同一层物料在受到本身质量的整数倍压应力时，堆积密度和体积发生相应的改变。因此，只需要对单层厚度的物料进行压实试验，根据拟合出来的方程算出其在承受自重所产生压力的整数倍时的厚度，即为数学模型中的各层物料的厚度值。

2 数据分析

田经烨等曾对九种粮食物料的自然堆积密度和压实密度进行了数据测量[5]，如表1、表2所示。

表1 九种物料自然堆积密度

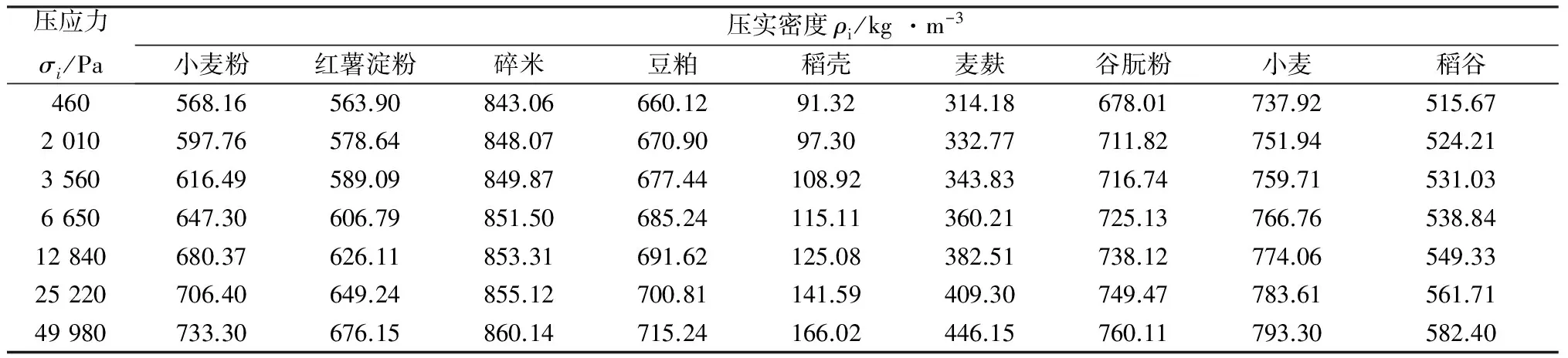
表2 九种物料在不同压力下的压实密度

根据表1和表2数据，文献[5]利用经验公式拟合出压实密度与压实应力的函数关系。但是在该文献中，用于测量自然物料堆积密度的量杯的高度与压实盒的高度有较大差异，因而压实盒内物料与量杯内物料的自然堆积密度不同，造成自然堆积密度测量装置测出的数据在理论上是偏大的[6]。因此，为了保证测量的准确性，应该使自然堆积密度测量装置中的量杯与压实盒等高，其它方法相同[7-9]。

另外，文献[5]中拟合出的函数关系并不能描述外力等于零的情形，这样无法完整描述试验中压实密度与压实应力的关系。

压实应力与堆积深度之间关系对于工程应用非常重要，因此，根据本研究提出的数学模型和文献[5]中的测量数据进行了二者关系的推导。

3 数据处理

相关学者之前已经做过九种物料的自然堆积密度与压实密度试验。只是自然密度测量试验方法及使用的经验公式存在些问题。为了避免不必要的重复试验劳动，只需想办法修正九种物料的自然堆积密度数据及寻找更合理的经验公式来拟合数据即可。

3．1 经验公式的改进

为了描述压应力为零时堆积密度变化的情形，笔者将之前的经验公式进行了改进，在公式中引进了初始量，即：

(5)

式中，ρi为物料的压实密度，kg/m3；ρ0为物料的自然堆积密度，kg/m3；σi为压实应力，kPa；a、b为经验公式系数，通过拟合方程后得到。

3．2 自然堆积密度数据的修正

先将各个物料的压实密度试验数据利用公式(5)进行拟合，拟合出的自然堆积密度值与试验值进行对比，拟合出来的值如果比试验值略小，则使用拟合出来的值作为ρ0的真实值；如拟合出来的值比试验值小很多或者比试验结果大，则将试验结果的值赋于ρ0，再重新拟合一遍，得出来的ρ0即为自然堆积密度修正数据。修正后的试验数据经过整理后，见表3。

表3 修正后的九种物料自然堆积密度

对比表1与表3可知，在表3中对豆粕、稻壳、麦麸、谷朊粉、小麦、稻谷的自然堆积密度数据都进行了修正，其它物料的数据没有变。

3．3 公式拟合

利用表2及表3数据，代入公式(5)进行拟合，即可得到试验用物料的压实密度与压实应力关系方程，如表4所示。

表4 压实密度与压实应力的关系

从表4中可以看出，大部分物料的拟合方程的函数相关性都在0.99以上，函数相关性最低的小麦也在0.95以上，所以表4的各个物料的拟合方程在实际估算应用上的可靠度与实用性较高。有必要指出的是，由于函数相关性不为1，红薯淀粉与碎米由表4中的公式算出的自然堆积密度值稍大于表3中相应的修正值，但误差不大，处于合理范围内。

4 物料堆积密度变化与堆积深度的关系

由公式(4)变形，得出物料厚度与压实密度的关系公式:

(6)

根据数据模型中的理论，利用表2数据与公式(6)求得的各层物料的厚度进行叠加，就能得到的堆积深度Hi，即：

(7)

从公式(6)、公式(7)即可以得到物料的堆积密度与物料厚度的关系。以小麦粉为例，相应数据如表5所示。

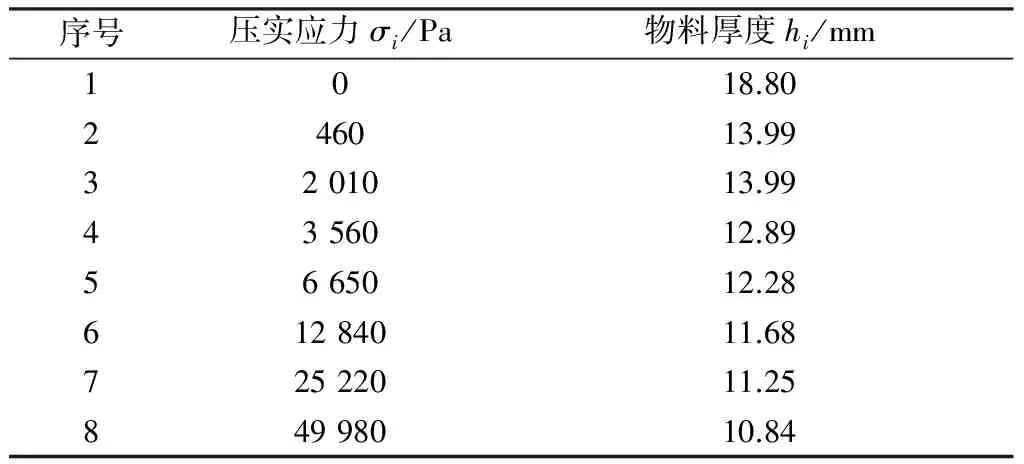
表5 小麦粉的压实应力与物料厚度的关系

利用表5中的数据及公式(5)进行拟合，得到小麦粉的厚度与压实应力的关系式

。

(8)

它的函数相关性R2=0.997 7，与试验数据契合度非常好。

由公式(2)可得出试验中的每份小麦粉所产生的压实应力σb=77.888 Pa，在压实应力试验值范围内, 以σb为步长，根据公式(8)进行线性插值，得出物料厚度进行累加，即为小麦粉的堆积深度。然后以60步为距离选取插值点，加上首尾两点，共选取12个点。选取点的相关数据及曲线如表6与图2所示。

表6 小麦粉压实应力与堆积深度的关系

图2 小麦粉的堆积深度与堆积压力关系曲线图

考虑到物料在初始厚度值时压实应力为0，利用公式(5)对表6中的数据拟合，得出小麦粉的压实应力与堆积深度的关系式:

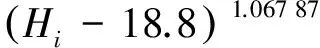
(9)

公式(9)的函数相关性R2=0.999 99，说明利用公式(9)可以在0至7.4 m的范围内，可以非常精确的描述小麦粉的堆积深度与压应力之间的关系。

5 在螺旋输料设备计量中的应用

在各种类型的螺旋输料设备下料量的计算中，普遍利用螺旋的一个螺距理论容积的特点进行估算计量[10-13]，即：

S=δ·m螺·t·n电/60

，

(10)

式中，S为下料量，kg；δ为物料的填充率；m螺为螺旋一个螺距的容积物料的质量，m3;t为时间，s；n电为电机转速，r/min。

这种算法的前提是把物料看作一个整体，并且假定物料的δ和m螺为定值，m螺为定值的前提是假定料仓中的物料堆积密度是不变的。而实际下料过程中，出料口的物料的堆积密度是逐渐减小的，这样测出来的填充率也是不断减小的。如果按照公式(6)估算物料的下料量的话，对一些堆积密度变化较大的物料，会产生较大的计量误差。

如果把物料看作是若干层物料堆积而成的话，采用前文所建立的数学模型及公式(10)分别计算每层的物料数据，再将所计算的数据进行整合，则可以有效提升体积计量法的估算精度[14]。

6 结论

(1)利用等质量分层法建立了粉料堆积密度的数学模型，可描述物料压实密度与堆积深度的关系。

(2)对物料压实应力经验公式进行改进，所得结果与试验数据契合度好。

(3)在螺旋下料应用中，结合本文所建立的数学模型及经典体积计量公式进行下料估计，可以有效提高体积计量法的计量精度。

[1] 谭生禄,冶廷虎.原盐计量包装秤中螺旋输送器的设计计算[J].盐业与化工，2007,36(5):46-49.

[2] 川北公夫,小石真纯.粉体工程学[M].武汉:武汉工业大学出版社,1991.

[3] 张荣善.散料输送与贮存[M].北京:化学工业出版社,1994.

[4] 廖荣福,邱生祥,潘仁湖.Jenike型剪切测试仪在颗粒物料流动性测试中的应用[J].硫磷设计与粉体工程，2011(6):23-29.

[5] 田经烨,邱生祥,潘仁湖等.料仓中堆积物料密度变化的研究[J].粮食与饲料工业，2016(7):3-6.

[6] 周晓强.关于摩擦系数对颗粒堆积密度影响的研究[D].广州:华南理工大学,2013.

[7] 孔德玉.粉料堆积密度测定方法的改进及应用[J].实验室研究与探索，2000,19(5):46-49.

[8] 沈建锋,朱曙光,刘心志,等.不同粒径稻壳粉堆积密度试验研究[J].可再生能源，2008,26(5):49-52.

[9] 王 静,杨秀芳,邹新武,等.茶与茶制品紧密堆积密度测定方法研究[J].中国茶叶加工,2014(4):25-26.

[10] 张西良,马 奎,王 辉,等.颗粒尺寸对螺旋加料机定量加料性能的影响[J].农业工程学报，2014,30(5):19-27.

[11] 赵占一,孟文俊,孙晓霞,等.垂直螺旋输送机中颗粒速度的分布[J].过程工程学报，2015,15(6):909-915.

[12] 梅 磊.螺旋卸船机垂直输送机理及试验研究[D].武汉:武汉理工大学,2014.

[13] 任建莉,胡维骏,王勤勇,等.垂直螺旋输送机气固两相流的试验及数值模拟[J].计算机与应用化学,2016,33(6):663-669.

[14] OWEN P J，CLEARY P W.Prediction of screw conveyor performance using the Discrete Element Method(DEM)[J].Powder Technology，2009，193(3):274-288.

(责任编辑：舒莲梅)

Relationship between bulk density and bulk depth of powder and its application

HE Fu-jun，FAN Hua， CHEN Xing,LIU Hong-yuan

(School of Mechanical Science and Engineering, Northeast Petroleum University, Daqing 168318，China)

In order to improve the measurement precision of mechanical system such as powder packing machine,we studied the relationship between the bulk density and bulk depth in theory,and improved the measurement method of natural bulk density experiment,and optimized the empirical formula of compacted density and compressive stress.The mathematical model of the relationship between bulk density and bulk depth was established by using the method of equal mass stratification.On the basis of the data of natural bulk density measurement of various materials,the correlation formula was fitted.Taking wheat flour as an example,the relationship between bulk depth and bulk density was established.According to the engineering application of screw material engineering,we proposed a new filler measuring method.

powder;bulk densify；compacted density；bulk depth; filler measuring

2017-03-31；

2017-04-20

黑龙江省科技攻关重大项目，编号：GA13A402。

何富君(1970-)，男，博士，教授，硕士生导师，研究方向为机器人技术。

樊 华(1986-)，男，硕士，研究方向为烹饪机器人。

10.7633/j.issn.1003-6202.2017.07.005

TS210.3

A

1003-6202(2017)07-0017-04