不同周期信号交叉口间的相位差优化模型*

鄢小文 徐建闽,2 荆彬彬

(1.华南理工大学 土木与交通学院， 广东 广州 510640； 2.东南大学 现代城市交通技术江苏高校协同创新中心， 江苏 南京 210096)

不同周期信号交叉口间的相位差优化模型*

鄢小文1徐建闽1,2荆彬彬1

(1.华南理工大学 土木与交通学院， 广东 广州 510640； 2.东南大学 现代城市交通技术江苏高校协同创新中心， 江苏 南京 210096)

为满足不同周期子区间协调控制的需要，提出对不同周期的信号交叉口实行大周期内协调控制的思想.通过分析不同周期下相邻交叉口间的车流到达规律，利用交通波理论建立了不同周期相邻交叉口间的延误模型，并提出了基于最小延误的不同周期交叉口间的相位差优化方法.最后以两个不等周期时长交叉口为例，利用VISSIM仿真对优化前后的协调控制效果进行对比.仿真结果表明，相位差优化后车辆的平均延误降低了13.60%，平均停车次数降低了6.43%，以此证实了该方法的有效性.文中研究为解决不同周期子区间的协调控制问题提供了新的思路与方法.

交通波理论；延误模型；大周期协调；相位差优化

交通信号控制特别是干道信号协调控制在缓解城市干线交通拥堵、减少尾气排放以及提升交通安全等方面具有重要作用.基于此，相关专家学者对干道绿波协调控制方法进行了较为深入的研究[1].研究思路主要集中在最大绿波带法和最小延误法.常用的绿波带法有图解法、数解法以及模型法.图解法[2- 3]是以几何作图的方法，通过不断地调整绿波带速和信号周期来确定相位差；数解法[4- 6]是通过寻找与实际交叉口间距最为匹配的理想间距从而确定绿波带速与相位差；模型法[7- 8]是通过综合考虑周期、相位差、行驶车速等因素建立混合线性规划整数模型，从而实现绿波带宽最大.最小延误法[9- 10]是先给出车辆通过交叉口的延误计算方法，然后建立基于干道车辆总延误最小的相位差优化模型，最后确定干线最优相位差.以上研究均假定干道各交叉口采用相同的信号周期时长，然而实际线控系统中，干线各交叉口受其交通流量、几何条件、行人过街等因素的影响，各交叉口实际所需信号周期往往并不相等.对于该问题，通常采取子区划分将信号周期相近的交叉口划在同一子区进行绿波协调控制，不同子区之间仍采用不同的信号周期，这割裂了子区间的联系，降低了绿波协调的效果.如何解决不同周期子区间的绿波协调控制问题已成为交通信号控制的迫切需求.梁杰等[11]突破传统干道绿波协调控制中公共周期的限制，以大周期内车辆行程时间最小为目标，提出了不同周期实施绿波协调控制的方法.张强等[12- 13]以路段上相邻的公共周期交叉口与双周期交叉口为研究对象，利用波动理论[14- 15]给出了非等周期下协调交叉口车辆排队模式及其长度计算方法.

综上可知，关于不同周期子区间的绿波协调控制目前仍鲜有研究.如何满足实际交通信号控制系统的需求，解决同一干道上不同周期子区间的协调控制问题以及如何扩展现有干道绿波协调控制方法以实现路网内不同周期干道间的协调控制显得尤为重要.基于此，文中利用波动理论，通过描述排队车辆的动态形成和消散过程，建立近饱和交通状态的交叉口延误模型，并将其应用到周期不等的信号交叉口间车辆延误的问题中，从而建立不同周期的信号交叉口间延误模型，并基于此模型，提出了基于延误最小的非等周期信号交叉口间相位差优化方法.

1 机理分析

1.1 交通波模型的推导

交通波理论是研究交通流状态改变过程中由于流体状态的改变而产生的冲击波的相关理论.如图1所示，相邻区域A和B的交通状态不同，密度为kA和kB，速度为vA和vB；S为波阵面，设S的速度为vW，交通波按照图中箭头x正方向运行.

图1 交通波分析Fig.1 Traffic wave analysis

根据流体力学相关理论，可知t时间内经过S的车辆数N为

N=vkt

(1)

即表达式(2)成立：

(vA-vW)kA=(vB-vW)kB

(2)

根据交通流模型可知

(3)

其中，qA和qB分别为区域A和B的车流流量，由此可得

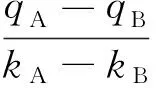
(4)

1.2 前提假设

为了简化建模过程，提出以下几点假设：①上游交叉口为固定信号配时，绿灯时间被充分利用；②协调相位绿灯期间直行车流以饱和流率释放，红灯期间左转车流以稳定流率到达；③初始时刻停车线处排队长度为0，初始周期队列完全消散，后续周期无二次排队；④不考虑车流的离散性以及右转车辆的影响.

1.3 基于交通波理论的延误模型

图2描述了一个车队从到达停车线到驶离交叉口的时空轨迹.假设在t=0 s时刻，车队中头车以速度v1、密度k1(对应于车头间距为L1)到达停车线处刚好遇红灯，红灯期间以SW1的波速从停车线处依次向后排队，绿灯期间以SWR的波速驶离停车线，车辆到达与车辆驶离产生的交通波相遇后形成新的交通波，以SWN的速度传播.r和g分别为红灯和绿灯时长，Xm为最大排队长度，tm为最大排队长度消散时间，tc为冲击波速从最长排队点传递到停车线处的时间.

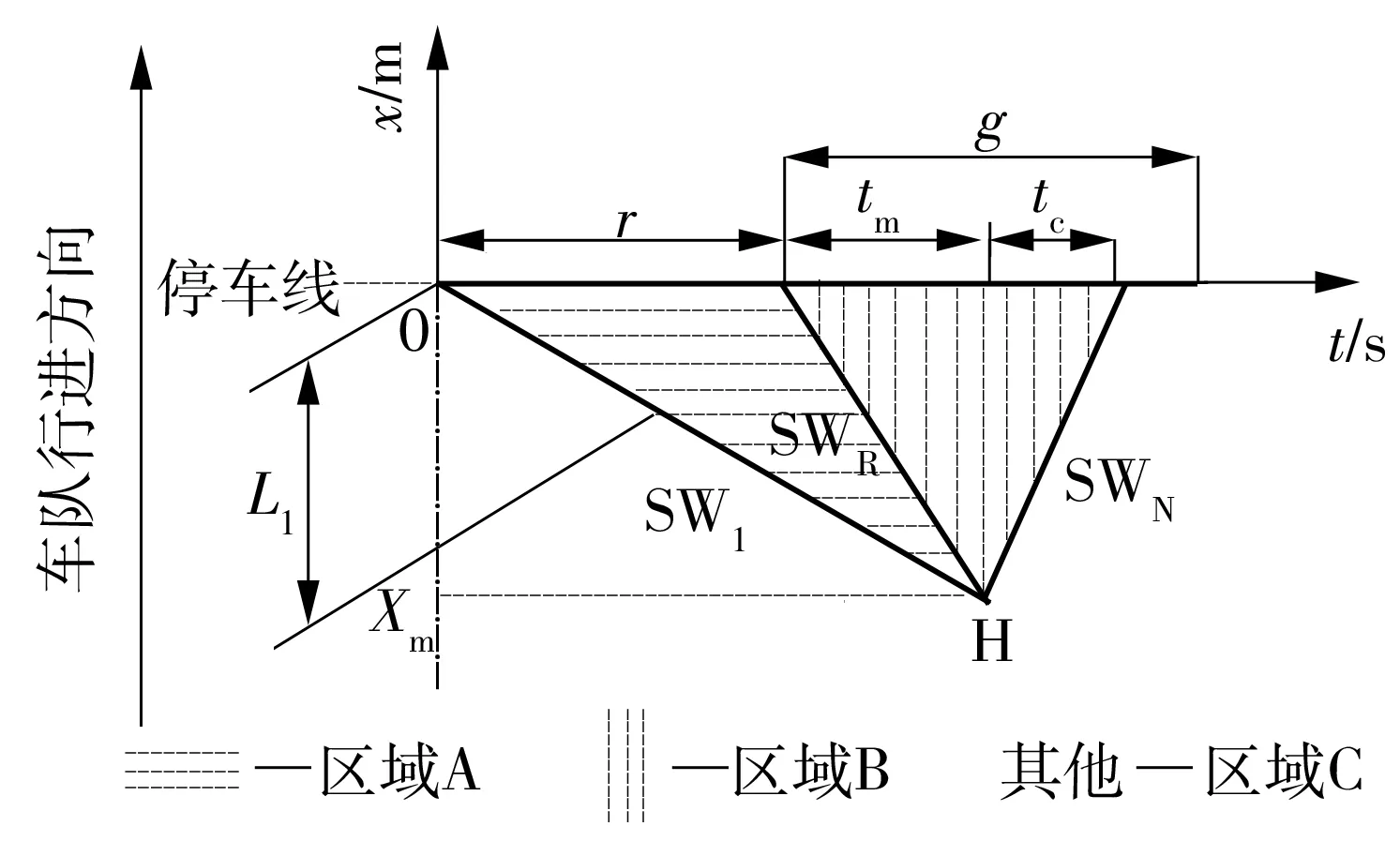
图2 车辆行驶时空轨迹Fig.2 Vehicle travel trajectory in time and space domains

车辆通过交叉口的总延误可以用每个区域的密度以及流率来表征.延误代表信号控制增加的额外行程时间，即

Td=Ts-Tn

(5)

其中，Ts、Tn分别为通过受信号控制和不受信号控制的交叉口所需的行程时间.

总延误计算公式如下：

(6)

式中，Ai表示区域i的时间-距离曲线所围成的面积，ki表示区域i的车流密度，kC表示区域C的车流密度.

由图2建立数学关系式：

(7)

解得：

(8)

则车均延误d为

(9)

其中,qa为车流平均到达流率，ka为平均车流到达密度,kj为交叉口阻塞密度,qm为停车线处最大驶离流率，km为交叉口最佳密度,C为信号周期长度,s为饱和流率.

2 不同周期信号交叉口间的延误模型

2.1 研究对象

如图3所示，上、下游两个相邻的信号交叉口U、D周期时长分别为CU和CD，路段长度为L，UT、DT为驶进路段的直行车流，UL、DL为驶进路段的左转车流，车辆在路段上行驶的平均速度为v，协调相位绿灯时长分别为gU和gD，红灯时长分别为rU和rD，相位为对称放行.忽略右转车流的影响，上行方向车流由西进口直行以及北进口左转车流构成，下行方向车流由东进口直行以及南进口左转车流构成.

图3 相邻交叉口间路段示意图

Fig.3 Schematic diagram of sections between adjacent intersections

2.2 协调路段间车流分析

为简化描述，定义类相位差，描述上游交叉口协调相位绿灯启亮后，头车到达下游交叉口的时刻与协调相位启亮时刻之间的时间差，满足公式：

(10)

其中，φ为上、下游交叉口的协调相位差,m为整数，使ψ∈(-C,C).

此处探讨周期不同的信号交叉口之间的协调问题，故定义一个大周期，取值由上、下游信号交叉口周期的最小公倍数确定.假设两信号交叉口周期近似满足关系：

n1CU=n2CD

(11)

n1、n2均为正整数，定义大周期的控制时段

T=n1CU

(12)

假定上游交叉口的配时方案确定，考虑其头、尾车到达时刻与协调相位绿灯启亮、结束时刻的关系，根据不同的相位差，可将延误分成两类：

(1)从上游驶出车流持续时长小于下游绿灯时长，若相位差满足关系：

(13)

则车队无延误.

(2)从上游驶出车队持续时长大于下游绿灯时长，车队总会受阻导致延误，详细分以下4种情形，如表1所示.

表1 4种延误情形Table 1 Four types of delay mode

针对第(2)类，每一股车流的延误有4种模式，分别考虑直行和左转两股车流驶入协调路段的情况，车队受阻情形如表2所示.

表2 16种车队受阻情形Table 2 Sixteen circumstances of blocked motorcade

2.3 不同周期信号交叉口间延误模型的建立

对16种情形按照延误大小排序，着重考察6种延误情形，即情形4、9、12、10、13、14，各种情形的满足条件及相位差取值范围如表3所示，对应的延误如图4所示.其中，tt、t1分别为从上游驶来的直行车流和左转车流的持续时长，vt、v1分别为直行和左转车流到停车线遇红灯的集结波速，vd、vs分别为车流由阻塞转向行驶状态的消散波速以及车流到达与行驶两种状态作用的冲击波速.根据交叉口实际信号配时关系选择相应延误模型，计算最优相位差.

表3 不同情形的延误模式Table 3 Different circumstances of signal delay modes

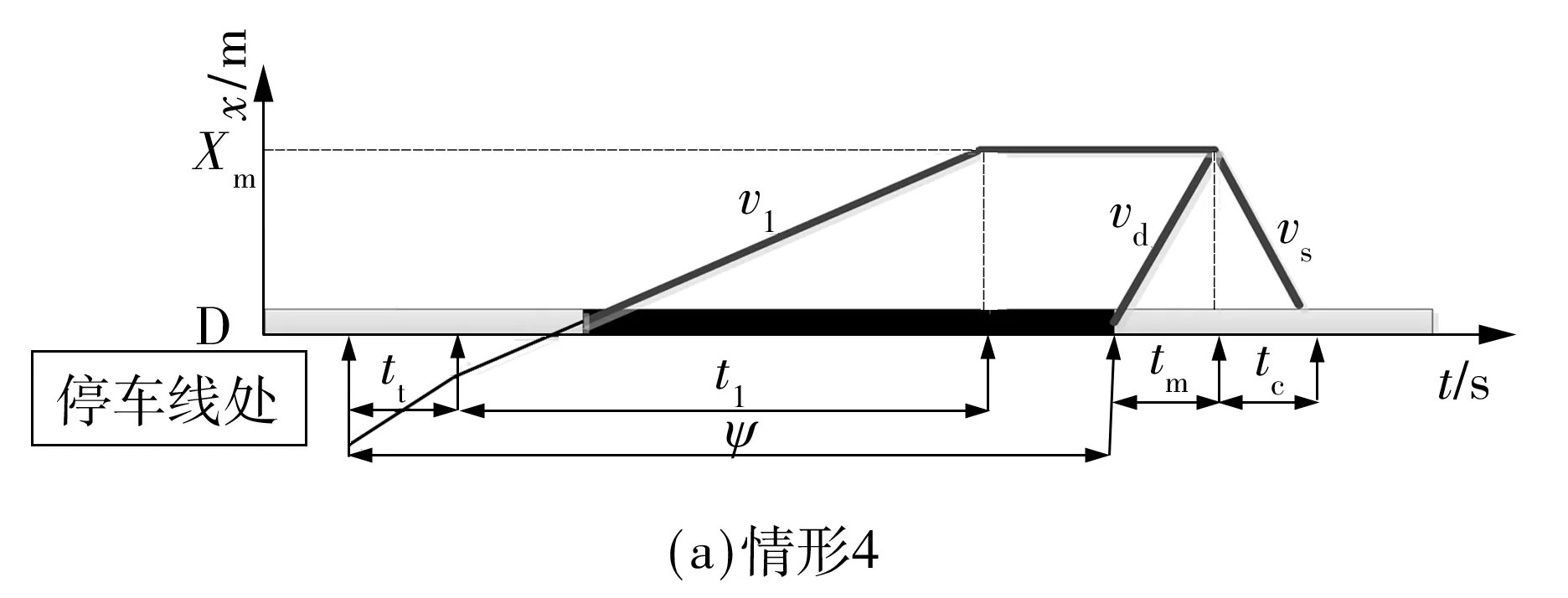
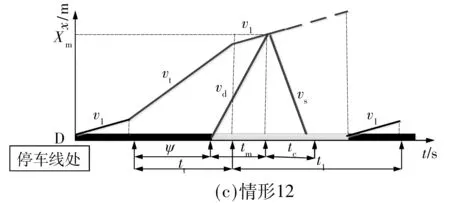
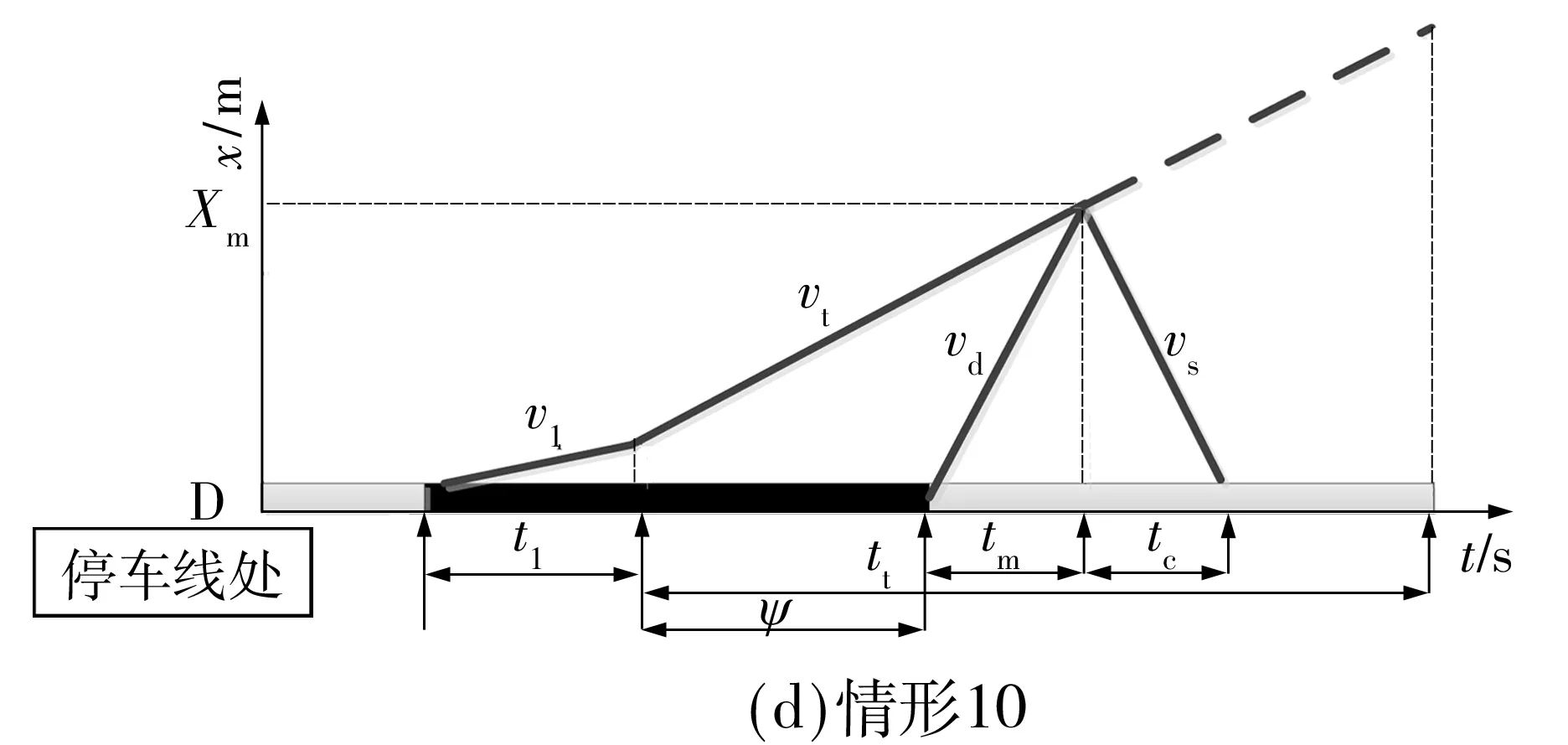
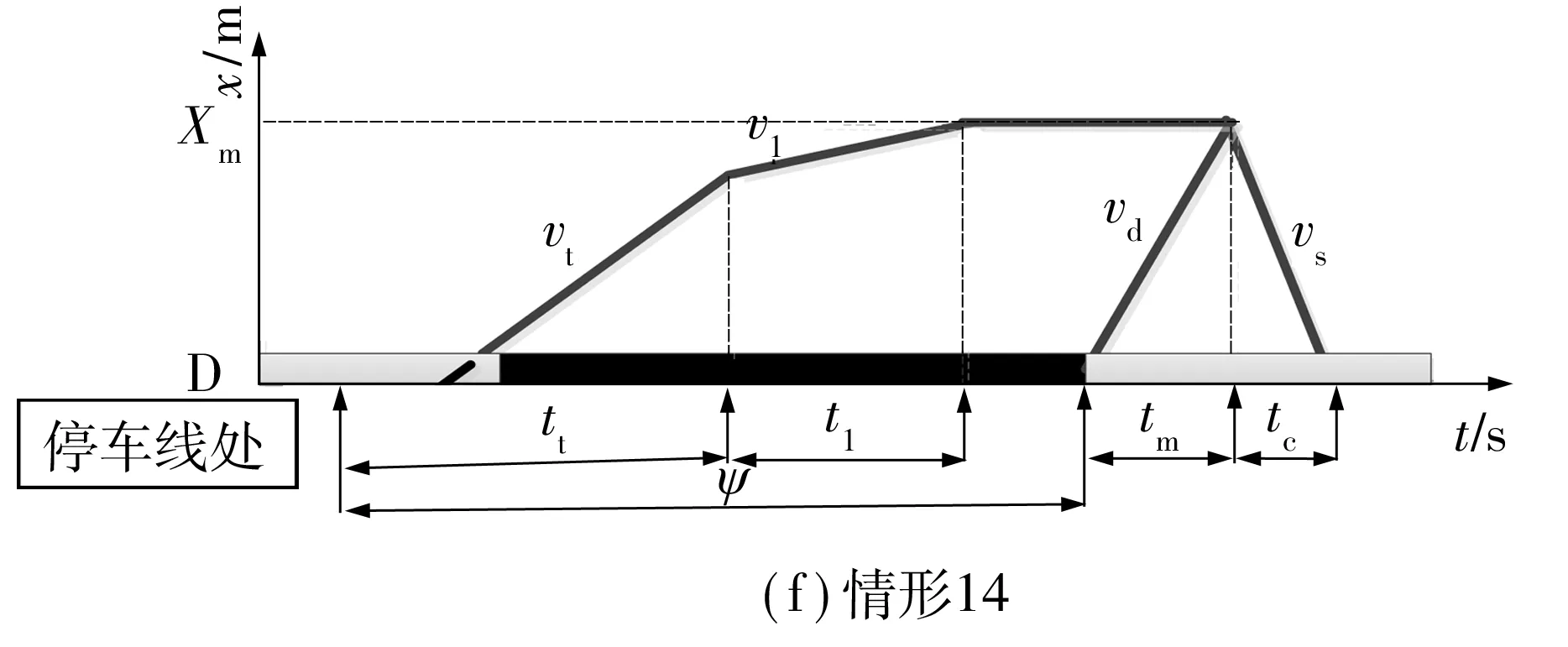
图4 不同情形的延误图示Fig.4 Delay diagrams of different circumstances

3 基于延误最小的相位差优化方法

在控制时段内，以下游信号交叉口为基准，确定一个相位差序列长度，控制时段每更新一次，就依次运行该相位差序列值.相位方案的过渡是个动态调整的过程，为了保障交通流的平稳安全运行，在控制时段的步序内每次相位差的变化适宜在小范围内进行.

首先根据周期确定控制时段T以及该时段内的n1个步序；然后根据交叉口各个周期驶出车队到达下游的信号状态依次计算控制时段T内的第1、2、…、n1个步序的最优相位差φ1、φ2、…、φn1.相位差优化流程如图5所示.

4 算例分析

假设一条两车道路段的上、下游交叉口进口道停车线相距800 m，上、下游信号交叉口周期分别为60和80 s，协调相位绿信比均为0.5，起始时刻排队车辆数为0，以240 s为大周期控制时段.考虑到相邻两交叉口间的车流运行于近饱和状态，采用格林伯模型描述交通流的流量-密度关系.模型参数计算如表4所示.

图5 相位差优化流程Fig.5 Offset optimization process

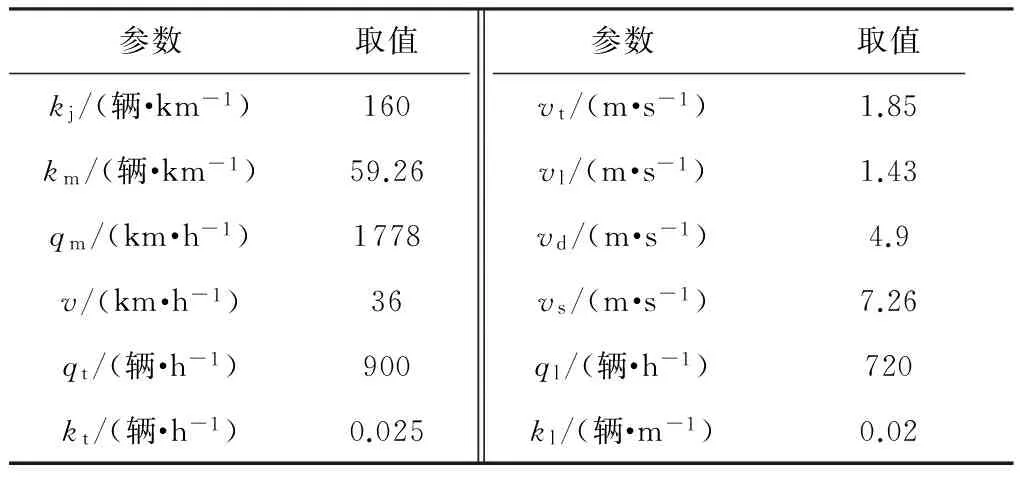
参数取值参数取值kj/(辆·km-1)160vt/(m·s-1)1.85km/(辆·km-1)59.26vl/(m·s-1)1.43qm/(km·h-1)1778vd/(m·s-1)4.9v/(km·h-1)36vs/(m·s-1)7.26qt/(辆·h-1)900ql/(辆·h-1)720kt/(辆·h-1)0.025kl/(辆·m-1)0.02

1)qt、ql分别为直行和左转车流到达流率，kt、kl分别为直行和左转车流到达密度.

以下游信号交叉口为基准，大周期为240 s,相位差循环周期与上游信号交叉口的驶出车流保持一致，为60 s，由此需要确定大周期内的4个控制步序，即每个控制时段内确定4个最优相位差.在每个控制时段内，根据不同的相位差取值范围，可能存在6种延误模式，如图6所示.根据图6计算延误与相位差之间的函数关系，根据相位差取值边界可将函数关系分为6段，图7所示为相位差落入不同取值区间的延误关系图，对应的延误-相位差分段函数如式(14)所示：

(14)

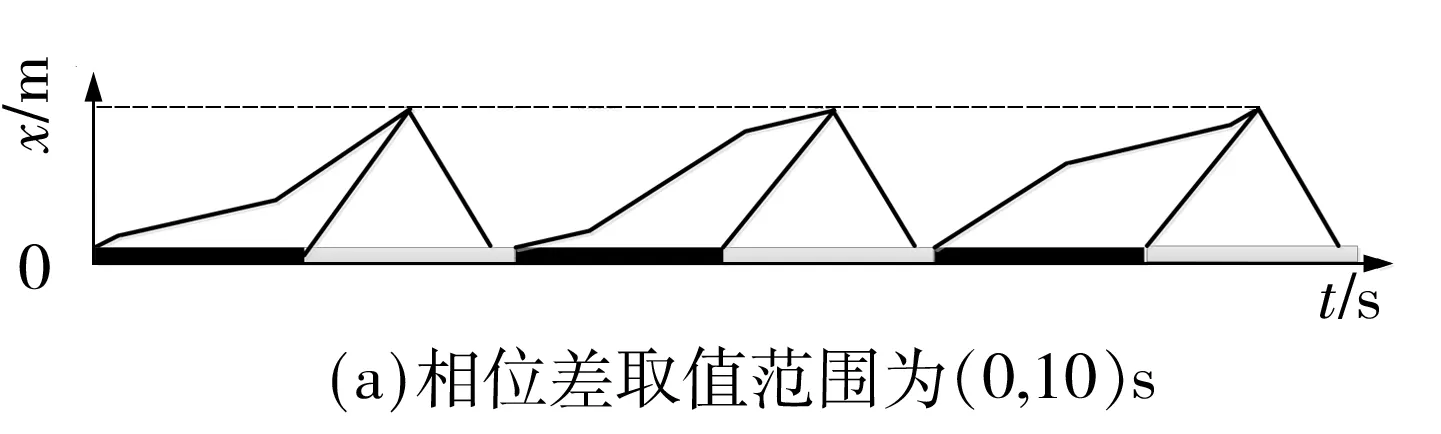
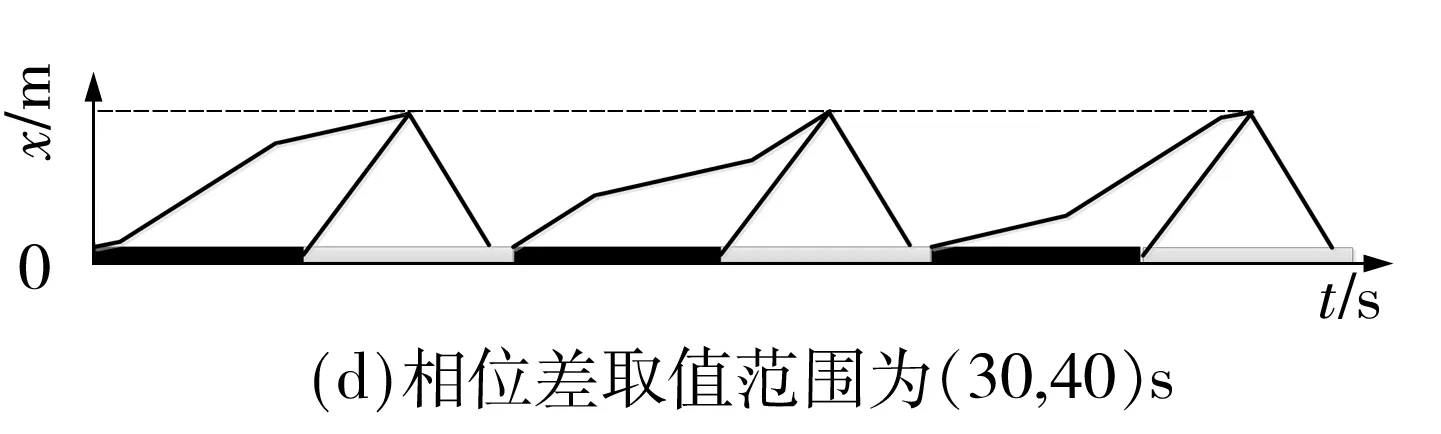
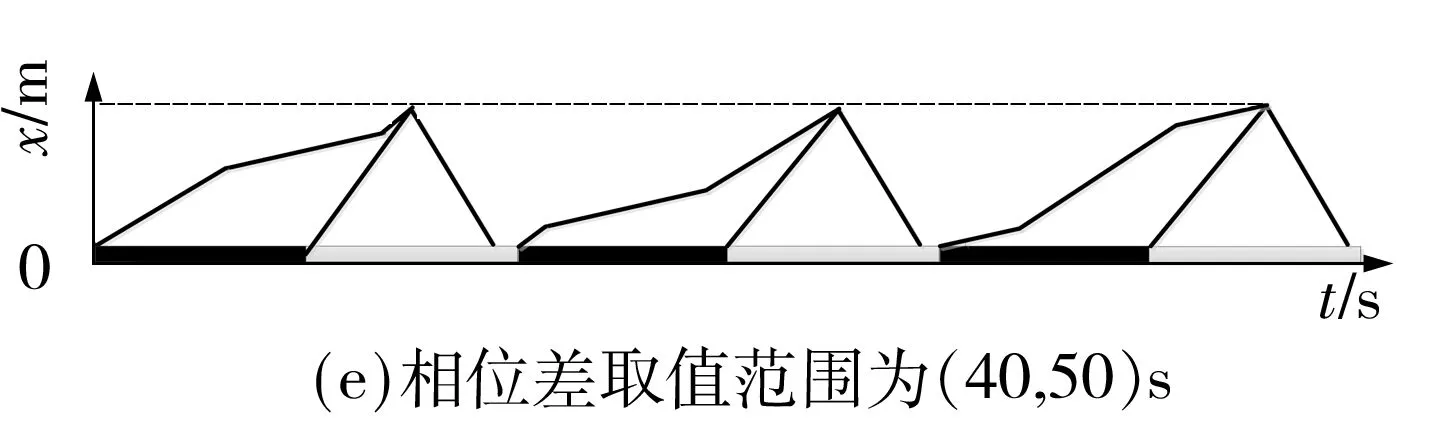
图6 不同相位差取值的延误图示Fig.6 Plots of vehicle delay under different offsets

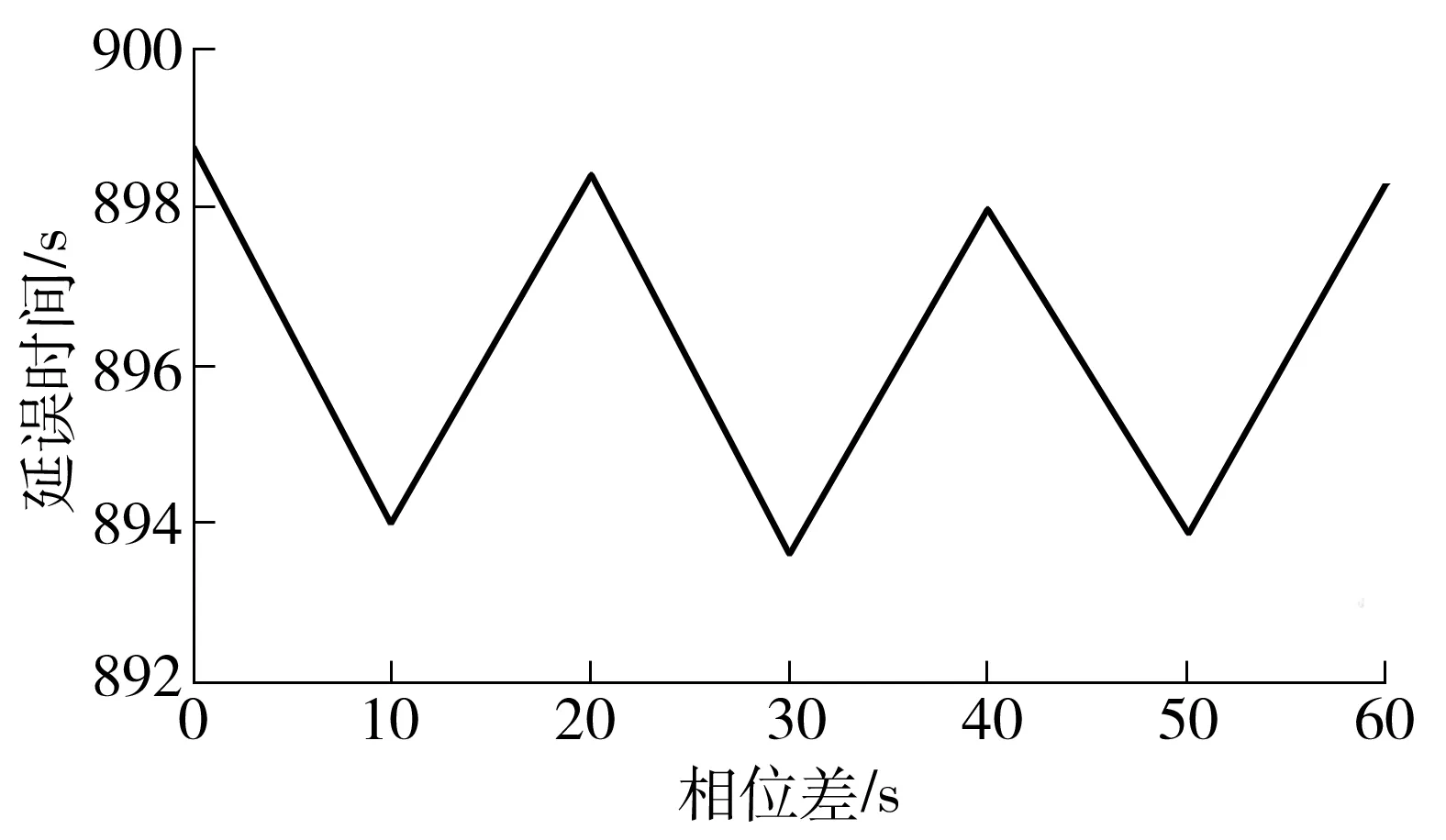
图7 延误-相位差关系Fig.7 Relationship between delay and offset

分析图7可知，当相位差落入不同的取值区间时，对应交叉口的延误计算公式不同.当相位差取10、30或50 s时，对应的延误取局部最小值.

在一个大周期内，可通过控制两个不同周期的交叉口间相位差序列值，使得控制时段内驶入协调路段的车流总延误最小.表5所示为初始相位差值落入不同的取值区间时，根据相位差优化方法得到的大周期内最优相位差序列值.

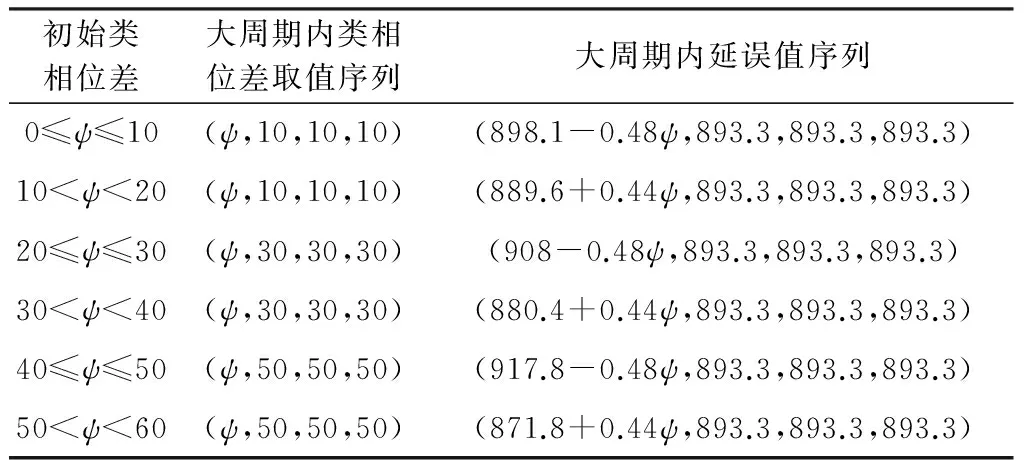
表5 相位差优化结果Table 5 Results of offset optimization

采用VISSIM仿真软件对模型计算得到的相位差方案进行仿真评价，根据上述模型计算所得的最优相位差序列值，通过改变仿真软件中的“随机因子”参数，模拟进行5次仿真试验，与单点不设置相位差方案以及采用等周期信号协调方案的结果进行对比，仿真结果以及不同方案的结果对比分别如表6、7所示.其中，方案1表示本相位差优化方案，方案2表示单点不设置相位差方案，方案3表示等周期信号协调方案(周期取80 s).

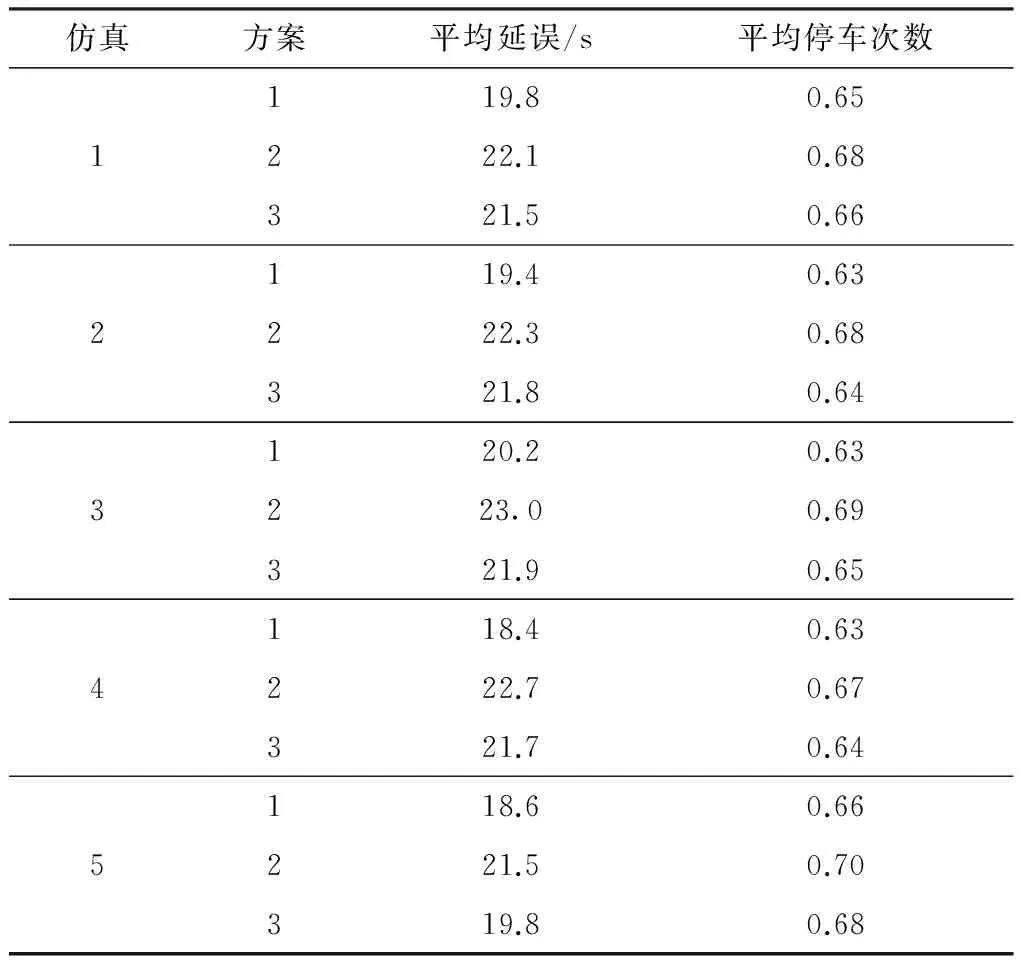
表6 VISSIM仿真结果Table 6 VISSIM simulation results

表7 不同方案的结果对比Table 7 Comparison of the results of different scenarios

仿真结果显示：与单点不设置相位差方案相比，相位差优化后，车辆平均延误降低了13.60%，平均停车次数降低了6.43%，平均延误和平均停车次数均得到了较大改善；与等周期信号协调方案相比，相位差优化后，车辆平均延误降低了10.21%，平均停车次数降低了2.18%，平均停车次数虽改善程度不大，但平均延误大大降低.因此应用此模型能够较好地改善区域路网的交通运行效果.

5 结语

以往关于停车延误协调控制的研究大多局限于信号周期相同的交叉口间延误模型的建立.由于不同周期子区间协调的需要，如何针对不同周期的信号交叉口建立合理的协调模型是亟待解决的问题.文中基于交通波理论，以大周期为考察时段，针对不同周期的信号交叉口，基于延误最小建立了大周期时段内的相位差优化模型.仿真结果表明应用此模型能够使车辆平均延误降低13.60%，平均停车次数降低6.43%.下一步考虑将此模型推广应用到不同周期干道的信号协调中，以真正实现由干线扩展到整个区域的信号协调，故此模型对于改善区域路网的交通运行具有重大意义.

由于建模中存在多项假设，本模型适用于交叉口直行和左转车流量较大、相比而言右转车流量可忽略不计的近饱和交通状态，这对模型的实际运用具有一定的制约性，下一步可考虑交叉口进口道存在初始排队长度的实际状况，对该模型进行进一步的改进，使该模型具有更广泛的适用性.

[1] 徐建闽.交通管理与控制 [M].北京：人民交通出版社,2007:142- 144.

[2] 常玉林,张其强,张鹏.城市干线双向绿波控制优化设计 [J].重庆理工大学学报(自然科学版),2014,28(12):108- 112. CHANG Yu-lin,ZHANG Qi-qiang,ZHANG Peng.Bidirectional green-wave signal control optimization design of city trunk road [J].Journal of Chongqing University of Technology(Natural Science Edition),2014,28(12):108- 112.

[3] 卢顺达,程琳.非对称相位相序方式下的双向绿波协调控制图解法的优化 [J].公路交通科技,2015,32(1):128- 132. LU Shun-da,CHENG Lin.Optimization of bidirectional green wave coordinated control graphical method under asymmetric phase sequence mode [J].Journal of Highway and Transportation Research and Development,2015,32(1):128- 132.

[4] 卢凯,徐建闽,李轶舜.进口单独放行方式下的干道双向绿波协调控制数解算法 [J].中国公路学报,2010,23(3):95- 101. LU Kai,XU Jian-min,LI Yi-shun.Algebraic method of arterial road coordinate control for bidirectional green wave under signal design mode of one-phase-one approach [J].China Journal of Highway and Transportation,2010,23(3):95- 101.

[5] 卢凯,徐建闽,叶瑞敏.经典干道协调控制信号配时数解算法的改进 [J].公路交通科技,2009,26(1):120- 125. LU Kai,XU Jian-min,YE Rui-min.Improvement of classical algebraic method of signal timing for arterial road coordinate control [J].Journal of Highway and Transportation Research and Development,2009,26(1):120- 125.

[6] 王殿海,杨希锐,宋现敏.交通信号干线协调控制经典数值计算法的改进 [J].吉林大学学报(工学版),2011,41(1):29- 34. WANG Dian-hai,YANG Xi-rui,SONG Xian-min.Improvement of classical numerical method for arterial road signal coordinate control [J].Journal of Jinlin University(Engineering and Technology Edition),2011,41(1):29- 34.[7] LITTLE J D,MARK C,GARTNER D,et al.MAXBAND:a versatile program for setting signals on arteries and triangular networks [R].Cambridge:Massachusetts Institute of Technology,1981.

[8] GARTNER N H,ASSMANN S F,LASAGA F,et al.MULTI-BAND-a variable-bandwidth arteries progression scheme [J].Transportation Research Record,1990,1287:212- 222.

[9] 万绪军,陆化普.线控系统中相位差优化模型的研究 [J].中国公路学报,2001,14(2):99- 102. WAN Xu-jun,LU Hua-pu.An optimal offset model for artery traffic signal control system [J].China Journal of Highway and Transport,2001,14(2):99- 102.

[10] 常云涛,彭国雄.基于遗传算法的城市干道协调控制 [J].交通运输工程学报,2003,3(2):106- 112. CHANG Yun-tao,PENG Guo-xiong.Urban arterial road coordinate control based on genetic algorithm [J].Journal of Traffic and Transportation Engineering,2003,3(2):106- 112.

[11] 梁杰,徐建闽.周期不同的多交叉口协调控制方法 [J].公路交通科技,2013,30(8):118- 123. LIANG Jie,XU Jian-min.A coordinated control method of multiple intersections in different cycles [J].Journal of Highway and Transportation Research and Development,2013,30(8):118- 123.

[12] 张强.非等周期协调信号交叉口间车辆排队模式及测算方法 [D].大连:大连理工大学,2013.

[13] 姚荣涵,王铁成,王建丽,等.协调信号交叉口间路段上的车辆排队模型 [J].吉林大学学报(工学版),2011,41(6):1585- 1591. YAO Rong-han,WANG Tie-cheng,WANG Jian-li,et al.Vehicle queue model for link between coordinated signalized intersections [J].Journal of Jinlin University(Engineering and Technology Edition),2011,41(6):1585- 1591.

[14] 王殿海,景春光,曲昭伟.交通波理论在交叉口交通流分析中的应用 [J].中国公路学报,2002,15(1):93- 96. WANG Dian-hai,JING Chun-guang,QU Zhao-wei.Application of traffic-wave theory in intersections traffic flow analysis [J].China Journal of Highway and Transport,2002,15(1):93- 96.

[15] LIU H X,WU X,MA W,et al.Real-time queue length estimation for congested signalized intersections [J].Transportation Research Part C,2009,17(4):412- 427.

Offset Optimization Model Between Intersections with Different Signal Cycles

YAN Xiao-wen1XU Jian-min1,2JING Bin-bin1

(1.School of Civil Engineering and Transportation,South China University of Technology,Guangzhou 510640,Guangdong,China;2.Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies, Southeast University,Nanjing 210096, Jiangsu, China)

In order to implement the coordination control between sub-regions with different signal cycles, the idea of coordination control between intersections with different signal cycles in a large period is proposed.Then, by analyzing the traffic arrival law between intersections with different signal cycles, a delay model based on the traffic wave theory is established, and an offset optimization method based on the minimum delay is proposed. Finally, by taking two signalized intersections with different cycle lengths as the examples, a VISSIM simulation is performed to analyze the effect of coordination control in a comparative way. Simulated results show that, after the coordination control, the average vehicle delay and the average number of stops decrease by 13.60% and 6.43%, respectively, which means that the proposed method is effective. This research provides a novel idea as well as a method for the coordination control between sub-regions with different signal cycles.

traffic wave theory; delay model; macro-cycle coordination; offset optimization

2015- 11- 25

广东省科技计划项目(2015A030401024) Foundation items: Supported by the Science and Technology Planning Project of Guangdong Province,China(2015A030401024)

鄢小文(1990-),女,博士生,主要从事智能交通系统、网络控制与优化、智能计算研究.E-mail:to_yanxiaowen@foxmail.com

1000- 565X(2017)06- 0044- 08

U 491.5+4

10.3969/j.issn.1000-565X.2017.06.008