三自由度直升机模型自适应模糊神经网络控制∗
2017-08-01李亚帅邵宗凯
李亚帅 邵宗凯
(昆明理工大学信息工程与自动化学院昆明650500)
三自由度直升机模型自适应模糊神经网络控制∗
李亚帅 邵宗凯
(昆明理工大学信息工程与自动化学院昆明650500)
针对三自由度直升机系统自身MIMO、较高阶次、非线性的特性,提出一种自适应模糊神经网络控制方法。首先运用牛顿-欧拉方程进行了机理模型的构建,利用线性二次型调节器得到控制系统的输出数据,该数据作为训练数据,将神经网络引入到模糊输入信号和模糊权值,应用自适应模糊神经网络推理系统设计控制器。通过Matlab对控制系统进行仿真,得到的仿真曲线与线性二次型调节器控制的仿真曲线作对比。结果显示:控制系统在论文提出的控制算法比LQR控制下能够更快地反馈控制信号,缩短了响应时间,其自主学习能力增加了系统在线控制的稳定性。
三自由度直升机;自适应模糊神经网络;线性二次型;动态性能
Class NumberTP273
1 引言
三自由度直升机系统模型由于其本身复杂特性,是现代控制理论研究验证的一个良好实验平台。但是由于其具有非常复杂的动力学特性和多变的飞行姿态,通常很难用精确的数学模型进行描述。为了解决三自由度直升机稳定实时控制问题,Shan J等应用运用同步根轨迹方法对直升机进行了控制[1],葛金来通过进行模糊自整定PID控制器的探究,设计的控制器对直升机系统的俯仰轴进行了较好的控制[2],于海丰依托内模的原理设计了无静差跟踪控制器对直升机的高度轴进行了实验分析[3],取得了不错的效果。
本文设计了一种自适应模糊神经网络控制器,通过仿真实验验证了该控制器能够三自由度直升机系统面对控制信号的改变,及时稳定地做出符合要求的动作反应。
2 三自由度直升机系统结构组成和模型构建
三自由度直升机模型如图1所示,其主要由下端底座、横杆、重物块和两个螺旋机翼组成。模型中重物块和两个螺旋机翼分别位于横杆的两侧,横杆通过万向节接头与下端底座相连接,螺旋机翼旋转产生的合力在水平方向的分力可以驱使直升机本体做旋转运动,在竖直方向的分力可以驱动直升机做俯仰运动。两个螺旋机翼靠相同的无刷电机提供动力。通过改变重物块在横杆上的位置来平衡螺旋桨端的提升作用力和重力。系统通过编码器来测量直升机的俯仰、偏航和滚动角度数据[4]。集电环安置在下端底座下部有利于信号的正常传输[5]。

图1三自由度直升机结构组成图
根据三自由度直升机系统模型的特点,针对其三个轴(三个自由度),根据牛顿-欧拉方程,构建飞行动力学模型[6]。
2.1 俯仰轴
三自由度直升机的俯仰是受两个机翼的升力Ff和Fb的合力升力Fh和本体重力G所决定的,当升力Fh大于重力G时,本体上升;反之本体下降。通过改变两个无刷直流电机的电压Vf和Vb可以改变升力Fh,现在假设俯仰角为零,直升机悬在空中处于平衡状态,即有微分方程等式:
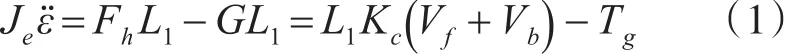
式中Je是俯仰方向的转动惯量;ε是俯仰方向角的加速度;Vf和Vb分别是两个无刷直流电机的电压,它们动作产生升力Fh;L1支点到电机的距离;Kc是无刷直流电机的升力常数;Tg是本体重力G所产生的有效力矩。

图2俯仰轴模型
2.2 横滚轴
三自由度直升机的横滚角是由两个螺旋桨产生的升力Ff和Fb之差所决定的,二者有差值,直升机本体则会产生旋转转动,合力在水平方向的分力会使直升机围绕支点旋转,因而可得到以下微分等式:
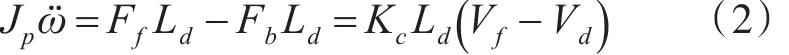
式中Jp是转动惯量;ω为横滚方向角的加速度;Ff和Fb分别为两个无刷直流电机产生的升力;Ld为支点到电机的距离。
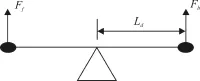
图3横滚轴模型
2.3 偏航轴
三自由度直升机偏航角的动力是由螺旋桨在横滚运动时产生的水平分力所提供的。假如两个螺旋桨有升力差,对于微小的角度,两个螺旋桨为直升机提供一个大小为G的合力Fg,就可以在水平方向上产生一个偏航方向的力矩,而使直升机产生偏航加速度。我们定义:顺时针方向为正,因而直升机横滚产生一个围绕偏航轴的负的加速度[7]。偏航方向的微分等式如下:

式中Jt是偏航方向的转动惯量;γ是偏航角加速度;p是偏航角,由于偏航角很小sin(p)≈p,故有:
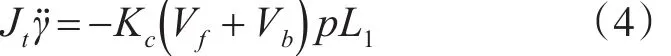

图4偏航轴模型
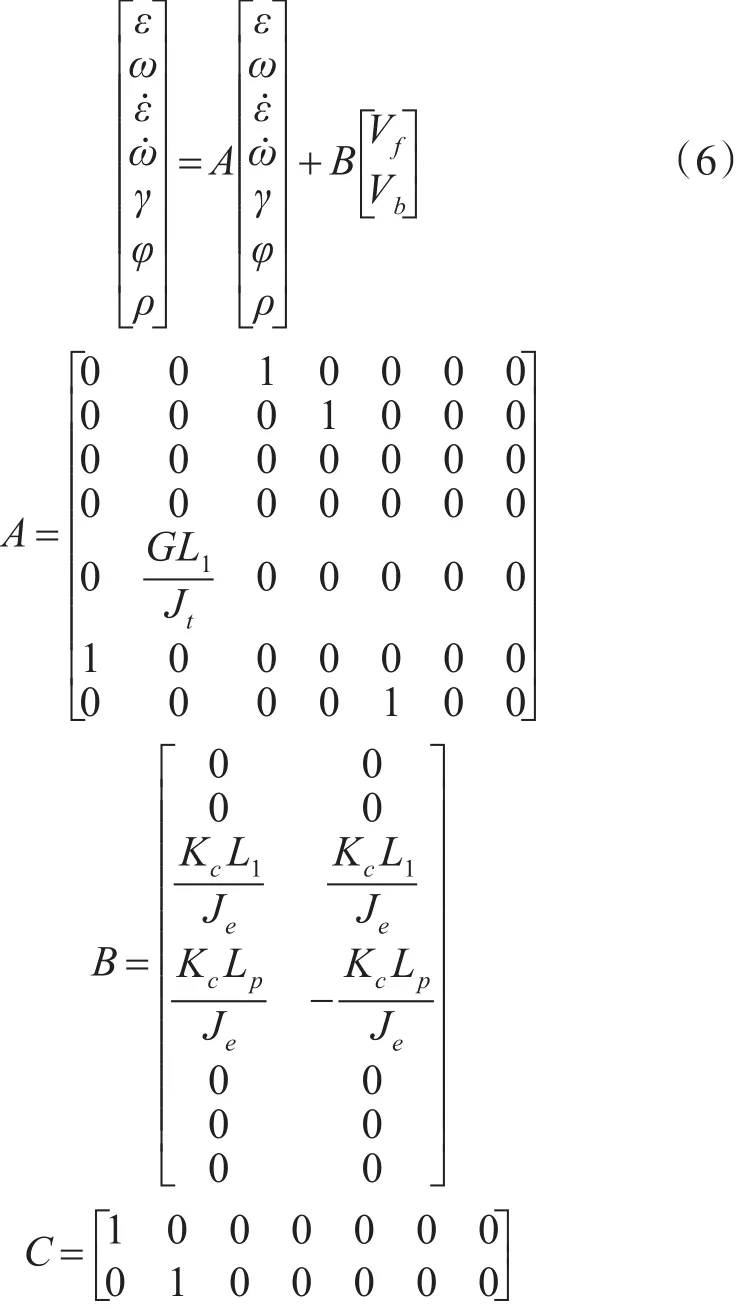
通过以上分析,可以得到研究对象的状态空间方程式:

其中:A为状态矩阵,B为控制矩阵,C为单位阵,τ为延迟时间阵,输入为uT=[Vb] Vf,俯仰角的积分φ=∫εdt,状态向量为xT=[] x1x2x3x4x5x6x7=[]
ε ω εωγ φp,因此得到如下状态方程:
3 控制器的设计
3.1 线性二次型调节器设计
对于一个线性系统,性能指标的选取定为:1)系统的状态变量;2)控制变量的二次型函数的积分,这种动态系统最优化控制问题就称作线性二次型调节器[8]。LQR是在通过建立线性模型的基础上通过引入对系统状态和输入能耗的评价的二次型积分函数作为评价函数,通过计算评价函数最小的方式而计算出状态反馈的反馈矩阵[9]。LQR的设计目的是要设计一个最优控制规则u() t,寻找最优状态反馈控制规律:

使得如下性能指标最小化:

其中Q、M是半正定矩阵,R是正定矩阵,Q和M分别是对状态变量和输入向量的加权矩阵,x是n维状态变量,u是m维输入变量,终端tf固定,终端状态x() tf自由。通过调用Matlab工具箱来解出LQR的解:
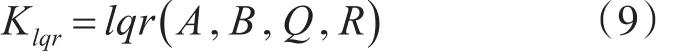
3.2 基于自适应模糊的神经网络控制器的设计
3.2.1 自适应模糊神经网络控制器的结构
自适应模糊神经网络系统(Adaptive Neu⁃ro-fuzzy Inference System,ANFIS)是指由服从模糊逻辑规则的一系列“if-then”规则所构造的,学习算法是依靠数据信息来对模糊神经系统的参数进行调整的,通过学习能够自动产生模糊规则的神经网络系统[10]。图5是自适应模糊神经网络系统原理图,由图5可知本文所采用的是具有五层的AN⁃FIS网络构建的模糊推理规则每层的介绍如下。

图5五层自适应模糊神经网络
第一层:输入层。该层节点主要是接收系统所给定的三自由度直升机系统三个轴的角度大小,其输出值等于输入值,将输入数据传输到第二层。
第二层:模糊化层,即将输入数据进行模糊处理。该层的每个节点对应着一个模糊语言变量,完成输入隶属函数的计算,从而实现输入变量的模糊化,其模糊集的隶属度函数采用高斯函数。第二层的每个节点的隶属度函数均由来确定,这里的x表示该节点的输入值,c和δ分别是该节点对应的隶属函数的中心和宽度。
第三层:模糊推理层。该层中的的所有点都对应着各自的模糊规则,用来推算出用于模糊推理计算的隶属度函数。
第四层:归一化算法层。该层与上一层共同进行模糊推理并输出模糊量;完成训练数据的后向传播,并将下一层的输入的精确数值模糊化,即完成三自由度直升机系统的输入角度的模糊化,计算公式为

第五层:输出层。完成去模糊化的功能,在实时控制阶段时将推理结果解模糊,最后输出直升机的实时运行角度;将训练数据即直升机的运行角度从该层反馈到该控制系统的网络中,为控制系统提供自主学习的训练数据[11]。
3.2.2 自适应模糊神经网络的学习算法
自适应模糊神经网络控制系统通过BP反向传播算法和最小二乘法对输入数据和输出数据建模,从数据集中提取相应信息,建立相应的模糊规则,使得生成的模糊推理系统能够更好地模拟出希望或实际输入值和输出值之间的关系[12]。
本文利用的是模糊控制自动提取模糊规则及选择合适的模糊隶属函数,加上自适应控制的自主学习能力,选取了Sugeno型模糊推理原理,利用已知的输入输出的数据进行训练,利用间接自适应模糊控制规则,在线逼近被控参数。该控制系统的训练样本是基于控制系统本身的输出的数据,从而使系统进一步得到了更为准确的训练,同时减少了逻辑推理的推理量和推理时间。该控制系统的学习误差函数为
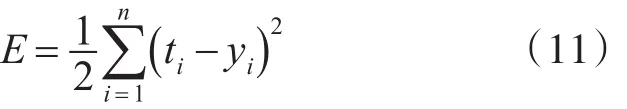
式中ti和yi分别为目标输出值和实际的输出值。在学习过程中对系统进行调整的系统参数主要是权值ω、高斯函数中心c和高斯函数高度δ。在计算学习的环节中对参数进行自行调整的运算方法为

式中k为运算迭代的次数,λ>0为计算学习速率。
将LQR得到的训练数据输入,Anfis训练生成一个Sugeno型作为初始隶属度函数的初始条件,取5条模糊规则。针对系统的输入,设定平衡点处俯仰角为零,建立三个模糊集,设定学习速率λ=0.6,根据俯仰角的线性化模型得到隶属度函数图形如图6所示。

图6俯仰角和俯仰角角速度隶属度函数图
4 仿真与实验研究
表1为本文做研究所用三的自由度直升机系统模型的基本参数。

表1 三自由度直升机模型基本参数
经过大量的仿真和实验,得到在LQR的权重矩阵Q和R的取值为

则可得到反馈增益为
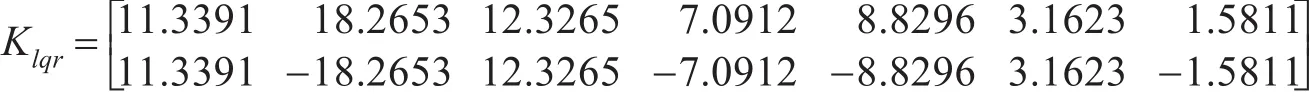
对俯仰轴和偏航轴分别进行以下操作:设置0<t≤5s时,俯仰轴的角度以6°/s的速度向上运动,横滚的的速度以10°/s按照顺时针方向旋转;5s后俯仰角达到30°的位置,横滚角达到50°的位置,此时两轴保持静止5s;10<t≤15s时俯仰轴的角度以6°/s的速度继续向上运动,而横滚角则以18°/s的速度逆时针旋转。实验仿真结果如图7所示。
仿真结果分析:从试验结果可以看出两种方法都可以使三自由度直升机系统达到较为理想的控制,但是基于自适应模糊理论的神经网络控制有着更好的控制响应。由图7(a)和7(b)俯仰角的跟踪曲线可以看出:LQR方法控制下系统由于模型是在平衡位置建立而且受到重力方面的干扰,在每个拐点附近(0<t≤2.5s,10<t≤12.5s和10<t≤11.5s)均产生状态抖动表现出动态性能的不稳定性,而自适应模糊神经网络控制方法在飞行状态发生改变时有较小的抖动,之后能够迅速达到稳定状态;根据图7(c)和7(d)横滚角的跟踪曲线可以看出,LQR方法控制下在拐点附近(0<t≤3s,5<t≤11s)表现出不稳定的状态抖动,而自适应模糊神经网络控制方法在拐点时发生微小超调后,能够稳定运行。
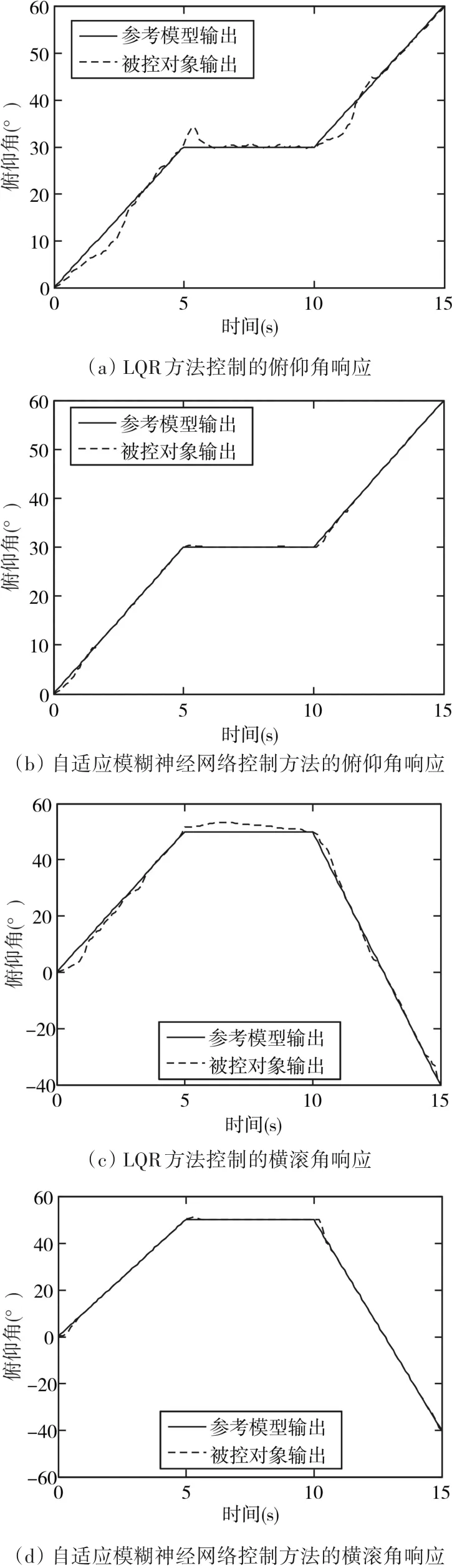
图7系统仿真结果图
5 结语
本文以三自由度直升机系统模型为研究对象,介绍了其结构组成和工作原理,分析了三个轴的动力学方程,建立了状态空间。提出了一种基于自适应模糊理论的神经网络控制方法,在线逼近了控制系统因状态的改变而产生的未知参数,并将该方法和基于LQR控制方法的运行结果进行了比较,仿真结果表明,两种方法都可以使三自由度直升机模型稳定运行,但是采用模糊自适应神经网络控制方法,系统不会在状态改变时刻产生过大的状态响应的飘移情况,具有更好的动态控制性能,较好地达到了预期设计控制效果。
[1]Shan J,Liu H T,Nowotny S.Synchronized trajecto⁃ry-tracking control of multiple 3-DOF experimental heli⁃copters[J].IEEE Proceedings-Control Theory and Appli⁃cations,2005,152(6):683-692.
[2]葛金来,张承慧,崔纳新.模糊自整定PID在三自由度直升机实验系统中的应用[J].信息与控制,2010,39(3):342-347. GE Jinlai,ZHANG Chenghui,CUI Naxin.Fuzzy Self-tun⁃ing PID Controller in the 3-DOF Helicopter Experimental System[J].Information and Control,2010,39(3):342-347.
[3]于春海,潘峰.基于逆系统的三自由度直升机内模控制设计[J].计算机工程与应用,2014,50(18):236-270. YU Chunhai,PAN Feng.Three DOF helicopter internal model control based on inverse system design[J].Comput⁃er Engineering and Applications,2014,50(18):236-270.
[4]王修岩,王莹,李宗帅.基于自适应逆的三自由度直升机控制研究[J].自动化与仪表,2014,29(1):11-14. WANG Xiuyan,WANG Ying,LI Zongshuai.Research of the 3-DOF Helicopter System Based on Adaptive Inverse Control[J].Automation&Instrumentation,2014,29(1):11-14.
[5]纪明达,李德伟,席裕庚.三自由度直升机的无静差预测控制[J].控制工程,2014,21(1):116-119,124. JI Mingda,LI Dewei,XI Yugeng.Offset Free Model Pre⁃dictive Control of 3 Dof Helicopter[J].Control Engineer⁃ing of China,2014,21(1):116-119,124.
[6]郭帅,陆耿,钟宜生.三自由度直升机模型辨识与控制[J].测控技术,2012,31(3):73-76,116-119. GUO Shuai,LU Geng,ZHONG Yisheng.Identification and Control of 3DOF Helicopter[J].Measurement&Con⁃trol Technology,2012,31(3):73-76,116-119.
[7]唐光辉,待洪波.三自由度直升机模型鲁棒控制器设计[J].华东理工大学学报(自然科学版),2010,36(5):105-111. TANG Guanghui,SHI Hongbo.Robust Controller Design for 3DOF Helicopter Model[J].Journal of East China Uni⁃versity of Science and Technology(Natural Science Edi⁃tion),2010,36(5):105-111.
[8]张金学,掌明.两轮自平衡机器人的LQR实时平衡控制[J].自动化与仪表,2013,28(5):5-9. ZHANG Jinxue,ZHANG Ming.Real-time Balance Con⁃trol for Self-balancing Two-wheeled Robot with LQR[J]. Automation&Instrumentation,2013,28(5):5-9.
[9]段镇.无人机鲁棒伺服LQR飞行控制律设计[J].计算机测量与控制,2015,23(8):2713-2715. DUAN Zhen.Robust Servo LQR Flight Control Law De⁃sign of UAV[J].Computer Measurement&Control,2015,23(8):2713-2715.
[10]孟劦,胡亚洲,陈晓.基于自适应模糊神经网络控制器的网络控制系统[J].计算机工程与应用,2015,51(18):90-93. MENG Xie,HU Yazhou,CHEN Xiao.Network control system based on adaptive fuzzy neural network controller[J].Computer Engineering and Applications,2015,51(18):90-93.
[11]刘金锟.智能控制(第2版)[M].北京:电子工业出版社,2012:32-42. LIU Jinkun.Intelligent control(Second Edition)[M]. Beijing:Electronics Industry Press,2012:32-42.
[12]钱夔,宋爱国,章华涛,等.基于自适应模糊神经网络的机器人路径规划方法[J].东南大学学报(自然科学版),2012,42(4):637-642. QIAN Kui,SONG Aiguo,ZHANG Huatao,et al.Path planning for mobile robot based on adaptive fuzzy neural network[J].Journal of Southeast University(Natural Sci⁃ence Edition),2012,42(4):637-642.
Adaptive Fuzzy Neural Network Control for Three Degree of Freedom Helicopter Model
LI YashuaiSHAO Zongkai
(Faculty of Information Engineering and Automation,Kunming University of Science and Technology,Kunming650500)
An adaptive fuzzy neural network control method is proposed for the multiple-input multiple-output(MIMO),high order and nonlinear characteristics of the three degree of freedom helicopter system.According to the characteristics of the three axes of the system,a mathematical model is established by using Newton's mechanics theory,the LQR method is used to set up the state feedback controller to get the input and output data,this data is used as training data.The neural network is introduced into the fuzzy input signal and fuzzy weight,it is introduced into the fuzzy in application of adaptive neural fuzzy inference system controller design nut signal and fuzzy weight,the control system is simulated by Matlab,the simulation curves obtained are compared with the LQR control simulation curves.Results show that the control algorithm proposed in this paper can control the signal faster than the LQR control signal,shorten the response time and increase the overall stability of the system.
three degree of freedom helicopter,adaptive neuro-fuzzy inference system,LQR,dynamic performance
TP273
10.3969/j.issn.1672-9722.2017.07.007
2017年1月11日,
2017年2月23日
李亚帅,男,硕士研究生,研究方向:飞行器的建模与控制。邵宗凯,男,博士,副教授,研究方向:智能信息处理,电机智能控制等。
