基于惯性系双积分的分布式POS抗干扰对准方法

白立建， 李建利，2， 翟风光

（1．北京航空航天大学惯性技术重点实验室，北京100191；2．卫星导航系统与装备技术国家重点实验室，石家庄050081）

基于惯性系双积分的分布式POS抗干扰对准方法

白立建1， 李建利1，2， 翟风光1

（1．北京航空航天大学惯性技术重点实验室，北京100191；2．卫星导航系统与装备技术国家重点实验室，石家庄050081）

分布式POS是一种基于惯性／卫星组合技术的柔性基线多节点高精度时空测量系统，是多任务航空遥感载荷高精度成像的关键装置。然而，外部扰动及节点间的柔性连接使得分布式POS不能采用传统解析粗对准方法进行高精度初始对准。为实现分布式POS系统在外部扰动下获得高精度初始姿态，提出了基于惯性系双积分的抗干扰对准方法，通过双积分去噪原理极大降低外部扰动影响，最后对算法进行了三轴转台实验和飞行实验验证。实验结果表明，该方法能够有效隔离载体的动态干扰，实现了分布式POS各节点初始姿态信息的高精度测量。

分布式POS；初始对准；惯性坐标系；抗干扰

Abstract：The distributed POS is a flexible baselinemulti⁃node high⁃precision measurement system based on SINS／GPS integrated navigation technique．It is the key equipment formultitask airborne remote sensors．However，the external disturbance and the flexible connection between nodesmake the distributed POS can'tadopt the traditional coarse alignment to obtain high⁃precision initial attitude．In order to solve the above problem，an anti⁃disturbance high⁃precision alignment algorithm based on double integral in inertial frame was proposed．Themethod can greatly reduce the disturbance effect by the double integral，and three⁃axis turntable experiment and flight experiment were carried out to validate the algorithm．The experimental results show that the proposed algorithm can remove the external disturbance and realized the high preci⁃sion measurement ofmulti⁃mode's initial attitude for distributed POS．

Key words：distributed POS;initial alignment;inertial reference frame;anti⁃disturbance

0 引言

机载对地观测系统是以飞机为观测平台，利用成像载荷获取地球表层大范围、高精度、多层次空间信息的一种尖端综合性技术［1］。随着高分辨率航空遥感技术的发展，新型航空遥感系统如基于同一飞行平台的高效多任务载荷联合成像系统、阵列天线SAR系统逐渐成为提高航空遥感成像效率和分辨率的有效手段。由于多个或多种观测载荷安装在飞机的不同位置，迫切需要开展分布式POS（Position and Orientation System）研究，解决多个成像载荷时空信息精确测量难题［2］。分布式POS是一种基于惯性／GPS组合及传递对准技术的柔性基线多节点高精度时空测量装置，已成为航空遥感的关键技术之一［3⁃4］。

分布式POS的初始对准是高精度导航的开始，初始位置、速度以及姿态信息决定着长航时的导航精度，是保障后续高精度实时组合导航的重要前提［5⁃6］。由于分布式POS子IMU分布在机翼两侧，易受外部环境等影响而发生扰动，IMU之间的柔性杆臂连接进一步恶化上述现象。由于传统解析粗对准的应用前提是准静态，故分布式POS不能采用传统解析粗对准方法进行高精度初始对准［7］。

针对上述问题，本文提出了一种基于惯性系双积分的抗干扰初始对准方法。该方法的基本原理是：根据陀螺的测量值实时跟踪惯性坐标系的变化，将加速度计的测量值投影在惯性坐标系下，当滤除固连载体对地加速度的影响后，可观测到重力加速度g在惯性坐标系中缓慢旋转，其运动轨迹是在以地球自转轴为主轴的一个锥面内，可以从g的漂移旋转中确定地理北向。基于两次积分去噪原理，此方法极大地减小了外部扰动对初始对准的影响。为验证算法有效性，进行了三轴转台实验以及飞行实验验证。实验结果表明，本文提出的抗干扰对准算法能够有效隔离载体的动态干扰，极大降低了外部扰动对分布式POS初始对准的影响，使分布式POS获取了高精度的初始姿态，显著提高了最终的导航精度。

1 坐标系定义

为了分析方便，介绍了此方法中采用的坐标系，具体如图1所示。

1）惯性坐标系（i系）：用OXiYiZi表示，坐标原点为地心，Xi、Yi在地球赤道上，Xi轴指向春分点（春分点是天文测量中确定恒星时的起始点，是赤道平面和黄道平面的交点之一），Zi轴指向地球极轴，由右手定则决定Yi方向。

2）地球坐标系（e系）：用OXeYeZe表示，与地球固连并随其转动，坐标原点位于地球质心，相对于i系，它以地球自转角速率旋转。Ze轴与地球极轴平行，且与地球自转方向一致；X轴位于赤道平面内格林威治子午线处；X、Y、Z轴相互正交，符合右手定则。

3）导航坐标系（n系）：坐标原点位于载体重心，导航坐标系的Xn、Yn、Zn轴分别表示载体当前所在位置的东、北、天方向。

4）载体坐标系（b系）：原点位于载体重心，Xb、Yb及Zb分别沿载体横轴指向右、沿纵轴指向前、沿立轴向上。

5）初始导航坐标系（n0系）：对准初始时刻与导航系重合，对准开始后不随载体运动而运动，相对地球表面固定不变。

6）初始地球坐标系（e0系）：原点位于地球中心，Ze0轴与地球自转轴重合，Xe0轴位于赤道平面内，从地心指向起始时刻的当地子午线，Ye0轴在赤道平面内，Xe0、Ye0、Ze0轴构成右手坐标系，对准开始后相对地球固定不变。

7）初始惯性坐标系（i0系）：Xi0轴在在当地子午面内且平行于赤道平面，Zi0轴指向地球自转方向，Xi0、Yi0、Zi0三轴构成右手坐标系，对准开始后相对惯性空间不变。

8）初始载体惯性坐标系（ib0系）：在初始对准起始时刻与载体系b系重合，对准开始后相对惯性空间不变。

2 基于惯性系双积分粗对准算法

分布式POS的子IMU悬挂在两侧机翼吊舱下，受扰动而不能静止，如采用传统解析粗对准方法进行对准，会造成较大误差，因此需要研究新的方法完成初始对准过程。近年来，一些研究者提出了一种以惯性坐标系作为参考基准进行晃动基座初始对准的新方法。惯性系粗对准的本质是利用加速度计测量两个不同时间点上的重力加速度在惯性空间的投影来确定北向［8⁃9］。但是上述提出的粗对准方法仅适用于低频摇摆晃动的舰艇惯导系统［10］，对于机载分布式POS受外部扰动等情况效果不大。因此，在上述方法的基础上，通过双积分去噪原理降低外部扰动影响，极大提高了分布式POS抗干扰能力。

其中，Cnn0（t）为初始导航系相对导航系的姿态转移阵，可以进一步分解成以下2部分：

式（2）右侧各部分根据坐标系定义可分别表示为：

式中，λ0和L0分别为初始时刻导航系统的经度和纬度，λt和Lt分别为初始对准阶段导航系统的经度和纬度。

式中，ωie为地球自转角速率。

根据式（6）和式（7），式（5）可表示为：

式中，Δλt为相对于初始位置的经度变化量，由于在初始对准过程中，外部扰动仅使惯导系统产生晃动而不发生位置的变化，故式（8）可简化为：

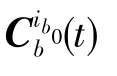
为了减小速度测量和加速度测量噪声干扰的影响，式（16）进行两次积分处理可得：

其中，

根据双矢量定姿基本原理，可求得常值矩阵：

3 基于惯性系双积分粗对准算法实验验证

为了充分验证惯性系双积分抗干扰对准方法的有效性，分别进行了三轴转台实验以及分布式POS飞行实验对抗扰动对准方法进行验证。

3.1 三轴转台实验

为了验证基于惯性系双积分的抗干扰对准方法能够在外部扰动的情况下进行初始对准，获取高精度的初始姿态信息，首先在三轴转台上进行了摇摆扰动半物理仿真实验，模拟真实环境中惯导系统受外部环境影响而发生扰动等情况。在外部扰动状态下采用惯性系双积分粗对准方法进行对准，观察对准结果是否满足应用要求。

实验中采用的POS导航系统，惯性测量单元采用高精度激光IMU，陀螺和加速度计的漂移分别为0．01（°）／h和50μg。在三轴转台实验中，首先将高精度激光IMU通过转接板安装于三轴转台台面并保持摆台静止，搭建POS系统，启动POS系统，实时采集IMU的输出数据，静止5min后分别按照表1设置三轴转台的运动参数（晃动幅度、晃动频率）进行运动5min，最后静止5min。具体实验装置如图2所示。

为了给IMU提供高精度姿态基准，先采用传统解析粗对准方法在前5min静止状态进行对准，然后进行纯惯性导航。纯惯性导航短时间内精度高，故以纯惯性导航结果为基准，对比传统对准方法和抗干扰对准方法分别在晃动过程中的对准结果。

受三轴转台运动幅度和频率的限制，进行了下面2组参数的振动，具体晃动幅度、晃动频率如表1所示。

表1 三轴转台运动参数Table 1 Motion parameters in tests

基于上述实验采集的数据和纯惯性导航获取实时高精度姿态基准，然后在晃动期间分别采用传统解析粗对准方法和惯性系双积分对准法进行初始对准。对准时间为300s，对应的对准误差在50s时开始显示，由于传统解析粗对准方法的对准误差较大，故没有显示在波形图中。具体对准误差图如图3、图4所示。

通过误差波形图可以看出：在外部扰动环境下，导航系统采用基于惯性系双积分对准法能够快速完成对准，水平姿态角在极短时间内收敛至0．005°以内，航向角在150s左右收敛至0．05°以内，满足实际应用需求。基于上述波形图数据，分别统计了对准方法在动态对准300s时的对准误差，具体数据如表2所示。

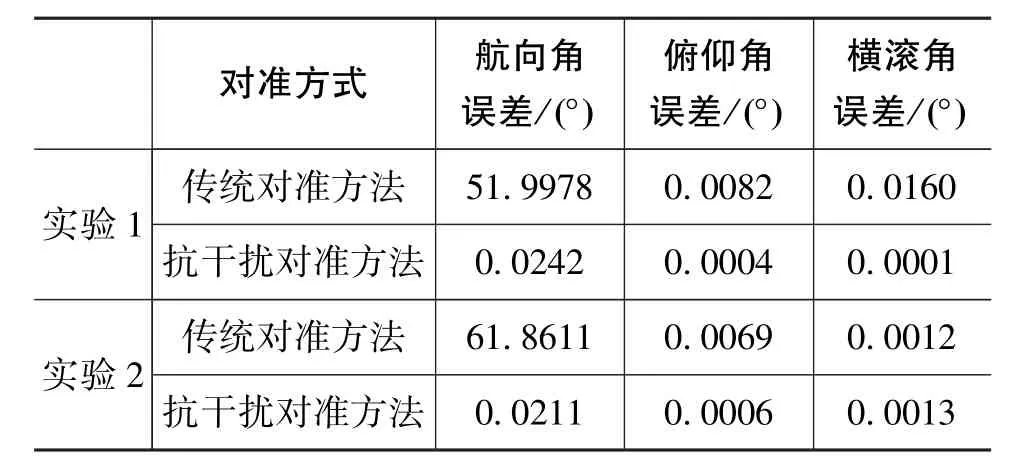
表2 POS对准误差统计Table 2 The attitude error of POS

根据误差统计表可以发现，传统解析粗对准方法受外部扰动不能进行精确对准，故此方法不能用于扰动基座初始对准，而惯性系双积分粗对准方法通过积分平滑的原理使导航系统不受外部扰动的影响而进行高精度初始对准。

3.2 分布式POS系统飞行实验

为了进一步验证惯性系双积分对准方法在真实环境下进行对准的有效性，分布式POS系统进行了相关飞行实验。机载分布式POS由安装在机体中轴上的主POS和对称分布在两侧机翼下方的两个子IMU构成。GPS天线安装于飞机背部，实时提供卫星导航数据。分布式POS系统装机示意图如图5所示。

在分布式POS系统初始对准过程中，飞机受到外部扰动的影响，比如发动机的振动、人员的走动或者阵风等。在此过程中，分别采用传统解析粗对准方法和惯性系双积分抗干扰法进行初始对准，获取不同的初始姿态信息，具体数据如表3所示。基于不同的初始姿态进行1h的纯惯性导航，以同时间段的GNSS导航结果为基准，通过对比2种导航结果的导航差，间接反映出初始对准的精度，误差变化图如图6所示。

表3 初始对准及导航误差统计Table 3 Initialalignment results and navigation errors

如图6所示，基于惯性系双积分对准方法的导航精度优于传统解析对准方法的导航结果。传统解析粗对准方法获得的初始姿态精度较低，严重降低了最终的导航精度。为了准确描述导航精度，最终的导航误差如表3所示。基于惯性系双积分对准方法求取的初始姿态，最终的导航精度约提高了70%。这一结果充分验证了惯性系双积分对准方法利用积分的原理去除外部干扰，能够进行高精度的初始对准。这种对准方法显著提高了分布式POS系统抗干扰能力以及环境适应性。

4 结论

本文提出了基于惯性系双积分的分布式POS抗干扰对准方法，利用加速度计测量2个不同时间点上的重力加速度在惯性空间的投影来确定北向，以及通过2次积分去除外部扰动对惯导系统的影响，并对所提出的方法进行了三轴转台实验以及分布式POS飞行实验验证。实验结果表明，本文提出的惯性系双积分对准方法能够去除外部扰动对导航系统的影响而进行高精度初始对准，显著提高了分布式POS系统的抗干扰能力以及环境适应性。

［1]安培浚，高峰，曲建升．对地观测系统未来发展趋势及其技术需求［J］．遥感技术与应用，2007，22（6）：762⁃767．AN Pei⁃jun，GAO Feng，QU Jian⁃sheng．Trend and tech⁃nology requirements of earth observing system［J］．Remote Sensing Technology and Application，2007，22（6）：762⁃767．

［2]Mostafa M M R，Schwarz K P．Digital image georeferencing from a multiple camera system by GPS／INS［J］．ISPRS Journal of Photogrammetry and Remote Sensing，2001，56（1）：1⁃12．

［3]Li J，Fang J，Du M．Error analysis and gyro⁃bias calibration of analytic coarse alignment for airborne POS［J］．IEEE Transactions on Instrumentation and Measure⁃ment，2012，61（11）：3058⁃3064．

［4]Li D R，Tong Q X，LiR，etal．Current issues in high⁃res⁃olution earth observation technology［J］．Science China Earth Sciences，2012，55（7）：1043⁃1051．［5]练军想，汤勇刚，吴美平，等．捷联惯导惯性系动基座对准算法研究［J］．国防科技大学学报，2007，29（5）：95⁃99．LIAN Jun⁃xiang，TANG Yong⁃gang，WU Mei⁃ping，et al．Study on SINS alignment algorithm with inertial frame for swaying bases［J］．Journal of National University of De⁃fense Technology，2007，29（5）：95⁃99．

［6]Gu D，El⁃Sheimy N，Hassan T，etal．Coarse alignment for marine SINS using gravity in the inertial frame as a refer⁃ence［C］．Location and Navigation Symposium，2008：961⁃965．

［7]高伟，郝燕玲，蔡同英．摇摆状态下捷联惯导系统初始对准技术的研究［J］．中国惯性技术学报，2004，12（3）：15⁃19．GAOWei，HAOYan⁃ling，CAITong⁃ying．Initial alignment of strapdown systems on swing base［J］．Journal of Chinese Inertial Technology，2004，12（3）：15⁃19．

［8]严恭敏，秦永元，卫育新，等．一种适用于SINS动基座初始对准的新算法［J］．系统工程与电子技术，2009，31（3）：634⁃637．YAN Gong⁃min，QIN Yong⁃yuan，WEI Yu⁃xin，et al．New initial alignment algorithm for SINS on moving base［J］．Sys⁃tems Engineering and Electronics，2009，31（3）：634⁃637．

［9]孙伟，孙枫．重力矢量在SINS快速系泊自对准中的应用研究［J］．压电与声光，2013，35（3）：368⁃371．SUNWei，SUN Feng．Resurface on the fastmooring self⁃algorithm for SINS based on gravity［J］．Piezoelectrics＆Acoustooptics，2013，35（3）：368⁃371．

［10]孙枫，曹通．基于重力信息的惯性系粗对准精度分析［J］．仪器仪表学报，2011，32（11）：2409⁃2415．SUN Feng，CAO Tong．Accuracy analysis of course align⁃ment based on gravity in inertial frame［J］．Chinese Journal of Scientific Instrument，2011，32（11）：2409⁃2415．

An ti⁃d istu rbance H igh⁃p recision A lignm en t for Distribu ted POS Based on Doub le In tegral in Inertial Fram e

BAILi⁃jian1，LIJian⁃li1，2，ZHAIFeng⁃guang1
（1．Science＆Technology on Inertial Laboratory，Beihang University，Beijing 100191; 2．Satellite Navigation Systems＆Equipment Technology Laboratory，Shijiazhuang 050081）

V243．5

A

1674⁃5558（2017）01⁃01335

10．3969／j．issn．1674⁃5558．2017．04．001

白立建，男，硕士，精密仪器及机械专业，研究方向为惯性／卫星组合导航系统。

2016⁃11⁃16

国家自然科学基金（编号：61571030）；国家高技术研究发展计划（编号：2015AA124001）；基础科研业务基金（编号：YWF⁃15⁃YQGD⁃001）