根据同时观测信息确定航天器姿态四元数的一种解析方法
2017-08-01范奎武
范奎武,郭 超
(海军驻航天一院代表室,北京100076)
根据同时观测信息确定航天器姿态四元数的一种解析方法
范奎武,郭 超
(海军驻航天一院代表室,北京100076)
介绍根据星敏感器同时观测几颗恒星的方向信息,用最小二乘法确定飞行器姿态的经典Wehba问题。针对用四元数描述飞行器姿态的情况,推导了的一种解析算法。观测5颗恒星实例的仿真结果表明,该算法能保证飞行器体轴系相对惯性系姿态的高精度。
航天器;姿态;四元数;星敏感器;算法
Abstract:This paper introduces the direction of information based on the star sensor observes a few fixed stars,with the least squaremethod to determine the attitude of the classic Wehba's problem.With quaternion to describe the aircraft attitude,an analytical algorithm is derived.Simulation resultwhich observes fixed stars show that the algorithm can ensure the high accuracy of the aircraft body axis relative inertial attitude.
Key words:spacecraft;attitude;quaternion;star sensor;algorithm
0 引言
为了提高航天器的导航与控制精度,通常采用捷联惯导与天文导航综合的导航系统。安装在航天器上的星敏感器可同时测量视场内的几颗恒星,不少于2颗恒星的测量信息就可以确定航天器的姿态,本文介绍推导其中的解析算法[1]。
1 问题的提出
描述航天器姿态的参数通常有Euler角、方向余弦矩阵、四元数[2],本文使用惯性系 OiXiYiZi(记为I系)和体轴系ObXbYbZb(记为B系)。为了确定姿态参数,要根据一定的算法对测量矢量进行数学处理,这些算法可以划分为两组:1)根据同时测量的几个矢量确定姿态的算法,称为 single⁃frame方法或者是局部算法;2)使用有关航天器动力学数据的动态滤波算法。
这些算法都基于Wahba形成的问题[3]:根据测量矢量ri(i=1,2,…,n),求出从I系到B系的转换矩阵CBI,该矩阵是正交阵,其行列式的值是1,它使下面的泛函取极小值:
可以把式(1)写成更方便的形式:
有求解Wahba问题的各种方法[4⁃5],为了求出最优矩阵,可以使用矩阵R的极分解:
式中,W为正交矩阵,S为正定矩阵。这时,按下面的表达式确定最优矩阵:
也可以使用矩阵R的SVD⁃分解法来求出最优解:
这些方法主要采用数值解法,没有给出精确解,这就给在航天器本体上使用时带来困难,下面将介绍推导根据测量矢量确定航天器姿态四元数的解析方法。
2 确定航天器姿态四元数的解析方法
设描述从I系到B系的转动四元数是Q,测量矢量ri(i=1,2,…,n),根据四元数与矢量在B系和I系中投影的关系,有:
这里,RiB、RiI理解为由矢量ri在B系和I系中的投影 [rixriyriz]T、 [riXriYriZ]T生成的标量部分为0的四元数,~Q是Q的共扼四元数。因为是单位四元数,所以其逆四元数与共扼四元数相等。式(7)的矢量部分是:
按照四元数的乘法规则:
利用四元数乘积的矩阵表示法,可进一步写成:
引入记号则有:
其展开式是:
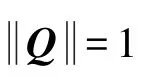
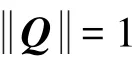
文献[7]和文献[8]研究确定用四元数描述航天器姿态时的最优解问题,指出最优四元数是与矩阵H的最小特征值对应的特征向量。
下面推导一种解析解法,把姿态四元数Q表示成:
Q=^Q°Θ (18)
式中,^Q是姿态四元数Q的某个估值,Θ是该估值的误差。引入矢量s,它使下面的泛函取极小值:
矢量s在B系和I系中的投影生成的3×1的列矩阵分别是:
它们与姿态四元数的关系是:
姿态四元数Q的某个估值是 ^Q,精确到绕矢量s有微小转动,即矢量s是由四元数Θ给出的转动的转轴,按照特征四元数的约定,从而有:
引入下面的记号:
于是,有:
把式(25)带入式(16),有:
矩阵G的特征方程为:
所以,λ2是矩阵G的特征方程的最小根,求与该根对应的特征向量,得出:
因为 Q^是姿态四元数Q的某个估值,所以下式成立:
把式(31)写成等效的线性齐次方程组:
描述转动四元数 ^Q的转轴上的单位矢量是ξ,ξ3×1表示由矢量ξ的分量生成的3×1的列矩阵,φ是有限转角。于是,就可以把上面的两个方程表示成:
选择矢量ξ如下:
带入式(35),得出:
由式(37)得出:
由此得出φ=α,进而有:
于是,在已有不少于2个不平行的测量矢量条件下确定姿态四元数的算法,归纳如下:1)根据式(17)确定矩阵H4×4;2)按式(20)计算sI、sB;3)按式(40)和式(41)计算^q0、^q;4)按式(23)计算
6)按式(29)和式(30)计算λ、z1、z2;7)根据式(25)得出姿态四元数Q=Wz。
3 仿真验证
设星敏感器坐标系与体轴坐标系重合,其光轴方向矢量是 [0 0 1]T,在星敏感器视场中有5颗恒星,朝向恒星方向的矢量在惯性系中的投影是:
这些方向矢量之间夹角的最大值为7.38°。进行1000次测量的仿真模拟,对于每个测量周期,用随机均匀分布的四元数Q表示B系相对I系的转动,而朝向恒星方向的单位矢量在体轴坐标系内的投影表示如下:
式中,δbk为Gauss随机白噪声,均值为0,均方差是6″。仿真计算过程中加权系数σi都取为1。
根据确定体轴系相对惯性系姿态的边界误差的大小估计算法的精度指标,按下式计算误差四元数Φ:
式中,¯Q是利用本文介绍的算法得出的姿态四元数的估值,误差四元数Φ描述微小转动,因此可以表示成:
式中,f= [f1f2f3]T是小转动矢量。 按下面的表达式计算确定体轴系相对惯性系姿态的误差:
结果如图1所示。计算结果表明,所推导的算法能够保证很高的确定飞行器体轴系相对惯性系姿态的精度,相对x轴、y轴的最大误差达到80″,相对z轴的最大误差仅为4″,其中确定星敏感器光轴的精度比其他两轴的精度高,这是使用小视场的星敏感器确定飞行器姿态时的所有算法的共同特性。
4 结论
本文针对用四元数描述飞行器姿态的情况,推导了根据星敏感器同时观测的几颗恒星的方向信息,用最小二乘法确定飞行器姿态的经典Wehba问题的一种解析算法。该算法需要的计算量少,并能保证为计算估值所需要的时间。对观测5颗恒星实例的仿真结果表明,该算法能保证飞行器体轴系相对惯性系姿态的高精度,可以在研制航天器高精度姿态控制系统时使用。
[1]ЕфименкоН В.Определениекватернионаориентации космического аппаратапо векторным измерениям взятым в один и тотжемоментвремени [J].Международный научно - технический журнал Проблемы управления и информатика,2016 (2):159⁃169.
[2]范奎武.用四元数描述飞行器姿态时的几个基本问题[J].航天控制,2012,30(4):49⁃53.FAN Kui⁃wu.The key problems of describing rigid⁃body attitude by using quaternion[J].Aerospace Control,2012,30(4):49⁃53.
[3]Wahba G.A least squares estimate of satellite attitude[J].Siam Review,1965,7(3):409.
[4]Farrell J L,Stuelpnagel J.C,Wessner R H,et al.A least squares estimate of satellite attitude[J].Siam Review,1966,8(3):384⁃386.
[5]Markley F L.Attitude determination using vector observa⁃tions and the singular value decomposition[J].Journal of the Astronautical Sciences,1988 36(36):245⁃258.
[6]以光衢.陀螺理论与应用[M].北京:北京航空航天大学出版社,1990.YI Guang⁃qu.Theory and application of gyroscope[M].Beijing:Beihang University Press,1990.
[7]Davenport P B.A vector approach to the algebra of rota⁃tions with application[R].Washington D.C:National Aeronautics and Space Administration,1968.
[8]Shuser M D.Approximate algorithms for fast optimal atti⁃tude computation[C].AIAA Guidance and Control Confer⁃ence,Palo Alto,CA,August7⁃9,1978:88⁃95.
Determ ination of Quaternion of the Spacecraft A ttitude by the Vector M easu rem en ts Taken in One and the Sam e M om en t of Tim e
FAN Kui⁃wu,GUO Chao
(Representatives Office of Navy of CALT,Beijing 100076)
U666.1
A
1674⁃5558(2017)03⁃01408
10.3969/j.issn.1674⁃5558.2017.04.010
范奎武,男,博士后,研究方向为飞行器总体设计、导航制导与控制。
2017⁃05⁃09
