基于多尺度排列熵和支持向量机的风力发电机组齿轮箱振动故障诊断

刘骊，贾嵘，李涛涛，尹浩霖，马喜平，郭泽维

（1.西安理工大学，陕西西安 710048；2.中国水电顾问集团投资有限公司，北京 100101；3.国网甘肃省电力公司电力科学研究院，甘肃兰州 730050）

基于多尺度排列熵和支持向量机的风力发电机组齿轮箱振动故障诊断

刘骊1，贾嵘1，李涛涛1，尹浩霖2，马喜平3，郭泽维1

（1.西安理工大学，陕西西安 710048；2.中国水电顾问集团投资有限公司，北京 100101；3.国网甘肃省电力公司电力科学研究院，甘肃兰州 730050）

针对传统方法难以精确检测风力发电机组齿轮箱非线性、非平稳振动信号以及现有许多故障诊断方法无法有效诊断齿轮箱早期故障的问题，首先引入排列熵算法对齿轮箱振动信号进行早期故障分析，进而引入多尺度排列熵算法实现原始振动信号的特征提取，得到故障诊断的样本数据，最后将其输入到建立的基于遗传算法优化支持向量机的诊断模型中，完成故障模式的识别与分类。仿真结果表明，该方法能够有效识别齿轮箱的异常工况，具有较高的故障诊断精度。

齿轮箱；多尺度排列熵；遗传算法；支持向量机；故障诊断

近年来，能源短缺与环境问题日益突出，世界各国对于新能源的发展日益重视。风力发电作为一种清洁可再生能源，在世界各国得到了快速发展[1-2]。但是，风力发电机组长期工作于室外恶劣的环境中，极易发生各种故障。齿轮箱作为风力发电机组的重要组成部分，由于其内部结构和受力状况复杂，在机组运行故障中所占比例较大，而齿轮箱一般又安装在几十米的高空，一旦发生故障，维修非常不便，严重影响了风力发电机组的安全稳定运行[3]。因此，开展风力发电机组齿轮箱故障故障诊断技术的研究对于改善指导风力发电机组的维护、降低机组维护费用和提高机组运行安全可靠性具有重要的意义。

齿轮箱故障诊断技术主要分为对原始信号的处理和对故障信息的识别与决策两个方面，目前，已有许多学者在这两方面完成了大量的研究工作。在信号处理方面，文献[4]采用自适应小波和奇异值分解的信号降噪方法提取风电传动系统的信号特征；文献[5]提出了基于小波包与倒频谱分析的风力发电机组齿轮箱故障诊断方法。但基于小波理论的信号处理方法，小波基函数的选择没有统一的标准，主要依赖专家经验，阻碍了其在齿轮箱故障诊断中的应用。文献[6-8]将EMD分解用于齿轮箱故障信号处理，应用效果较好，但EMD分解没有坚实的理论基础，且存在模态混叠现象。总之，现有方法对于处理齿轮箱故障信号，即非线性、非平稳的振动信号存在一定的缺点和不足，不能充分凸显信号特征。排列熵（permutation entropy，PE）算法是一种新的动力学突变检测方法，文献[9-10]已将单维度排列熵用于机械振动信号的特征分析，效果比较理想。但单维度排列熵在表征振动信号复杂度的能力有限。

另外，故障信息的识别决策方法主要有专家系统[11]、模糊理论[12]、神经网络[13]和支持向量机[14]等。这些方法各有优缺点。专家系统在知识的获取、维护以及推理等方面尚不成熟；模糊理论在处理复杂系统时，隶属度函数和模糊规则很难建立；神经网络需要在大量的训练样本，而实际运行中难以获取大量的数据样本；支持向量机具有结构简单、学习速度快、全局最优和泛化性好等优点，在贫样本情况下也可以达到较高的诊断精度。

本文采用多尺度排列熵（muti-dimension permutation entropy，MPE）分析齿轮箱故障信号以提取故障特征，利用支持向量机（support vector machines，SVM）进行故障诊断决策。通过风力发电机组齿轮箱实验数据的仿真分析，验证了该方法的有效性。

1 排列熵理论

1.1 排列熵的原理

排列熵是描述一维时间序列复杂度的的平均熵参数，与Lyapunov指数、分形维数等同类复杂度参数相比，计算简单，抗造性能强[15-16]。其基本原理如下。

给定一序列长度为N的时间序列{x（i），i=1，2，…，N}，对其进行相空间重构，得到重构信号：

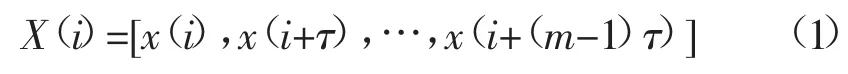
式中：m为嵌入维数；τ为延迟时间。

将式（1）中X（i）的m个数据按由小到大的顺序进行排列，得到：x（i+（j1-1）τ）≤x（i+（j2-1）τ）≤…≤x（i+（jm-1）τ）（2）式中：j1，j2，…，jm，表示各个元素在中的位置。

如果重构分量X（i）中存在2个元素的值相等，即

则按照j1，j2值的大小排列，如果j1≤j2，有

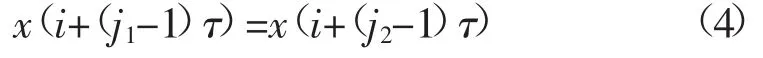
因此，对于任意的一个向量X（i）都可以得到一组序列模式

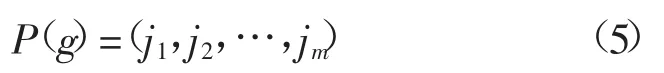
式中：g=1，2，…，k，且k≤m! ，m个不同的符号序列，最多有种排列方式，而只有一种符合序列P（g）。

计算每种符号序列出现的概率为

式中：l为P（g）出现的次数。

按照Shannon熵计算信号的排列熵为

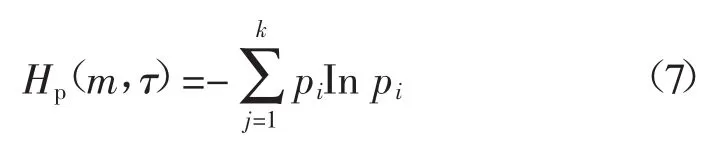
对其进行归一化处理，得

显然，Hp的取值范围是0≤Hp≤1。Hp的大小反映了时间序列信号的复杂度和随机性，其值越大，说明时间序列信号越复杂。反之，则说明时间序列信号越简单，越规则。所以，Hp值的变化反映和放大了时间序列的局部细微变化。

1.2 多尺度排列熵

由于单维度排列熵表征风力发电机组齿轮箱振动信号特征的能力有限，本文采用多尺度排列熵的方法。

定义信号的多尺度向量为

式中，mi为第i个嵌入维数，i=1，2，…，n。

在嵌入维数为mi时，信号的多尺度排列熵为

定义信号的多尺度排列熵为

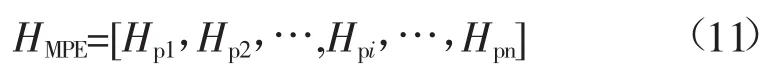
多尺度排列熵表征了振动信号特征的特征向量，而HMPE中的Hpi表征了振动信号在嵌入维数为mi时的复杂度，即振动信号若有n个维度，则就有n个特征。当多尺度向量直取其中的一个维数时，多尺度排列熵就变为了单维度排列熵。

2 基于遗传算法优化SVM的故障诊断模型

2.1 SVM参数的优化

SVM是在统计学习理论架构下，实现结构风险最小化原则的一种新的机器学习方法，在机械故障诊断领域得到了广泛的应用[17-19]。径向基核函数的宽度σ2和惩罚因子C是SVM诊断模型建立所需要的2个主要参数，2个参数的选取是否合理，直接影响到支持向量机故障识别与诊断的正确率，本文利用遗传算法的全局随机搜索能力对其参数σ2和C进行优化调整。其主要思路是先对SVM的2个参数σ2和C编码生成染色体，继而对染色体根据适用度函数值进行复制、交叉和变异操作，使其不断进化，最后得到使SVM分类精度达到最优的染色体。图1为本文建立的基于遗传算法优化SVM参数的流程图。

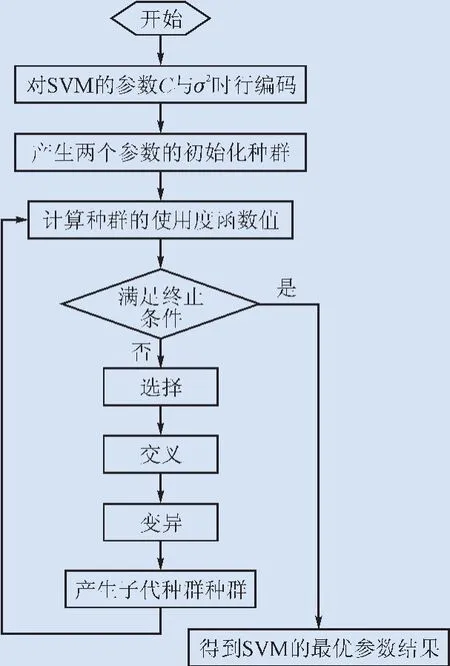
图1 GA优化SVM参数流程图Fig.1 GA optimization SVM parameters flow chart

2.2 诊断步骤

本文提出了一种多尺度排列熵和基于遗传算法优化SVM的诊断模型相结合的风力发电机组齿轮箱振动故障诊断方法，其具体的诊断步骤如下：

1）利用振动传感器采集齿轮箱在不同故障类型下的故障振动信号；

2）对每种故障振动信号进行分段；

3）利用MPE提取每段振动信号的特征向量，构成故障诊断的数据样本；

4）将每种故障的数据样本平均分成2组，分别作为遗传算法优化SVM诊断模型的训练样本和测试样本；

5）利用训练样本和测试样本对遗传算法优化SVM诊断模型进行训练和测试，完成故障的识别与诊断。

3 实验分析

本文将多尺度排列熵和基于遗传算法优化SVM相结合的故障诊断方法应用于江苏千鹏诊断工程有限公司的机械故障模拟及试验平台模拟的齿轮箱故障数据中，以验证本文提出方法的正确性与有效性。图2为齿轮箱机械故障模拟试验平台，主要由变速驱动电机、轴承、齿轮箱、轴、偏重转盘、调速器等组成。通过调节配重，调节部分的安装位置以及组件的有机组合快速模拟齿轮箱的各种故障。本文采集齿轮箱大齿轮在正常、点蚀和断齿3种状态下的故障振动数据，各采集15 360个点，采样频率为5.12 kHz，图3为齿轮箱在3种状态下的原始信号时域图。

图2 齿轮箱故障模拟实验台Fig.2 Gear box failure simulation test bed

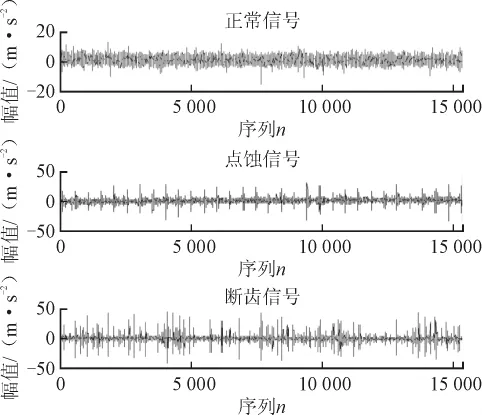
图3 齿轮箱3种状态的原始振动信号Fig.3 The original state of the gear box vibration signal

3.1 特征向量的提取

将齿轮箱在正常、点蚀和断齿3种状态下的原始信号分别分为30段，共分为90段，每段信号各512个点。利用多尺度排列熵进行特征向量的提取，本文选取多尺度排列熵的维数为[4，5，6，7，8，9]。以齿轮箱正常信号为例，进行特征向量的提取，图4为齿轮箱正常信号第一段信号的时域图，图5为其多尺度排列熵经归一化处理后的分布图。齿轮箱在点蚀和断齿时的特征向量提取方法与正常时的方法相同。表1为本文提取的特征向量，其中，H1，H2，H3分别为齿轮箱3种状态的前3段信号的特征向量，各有30组特征向量，受篇幅限制，本文只列出前3组特征向量。

图4 正常时的第一段信号Fig.4 The first paragraph of the normal signal

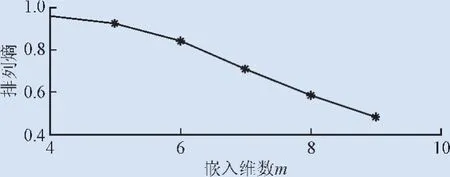
图5 第一段信号的多尺度排列熵Fig.5 Multi-scale permutation entropy of the first-stage signal

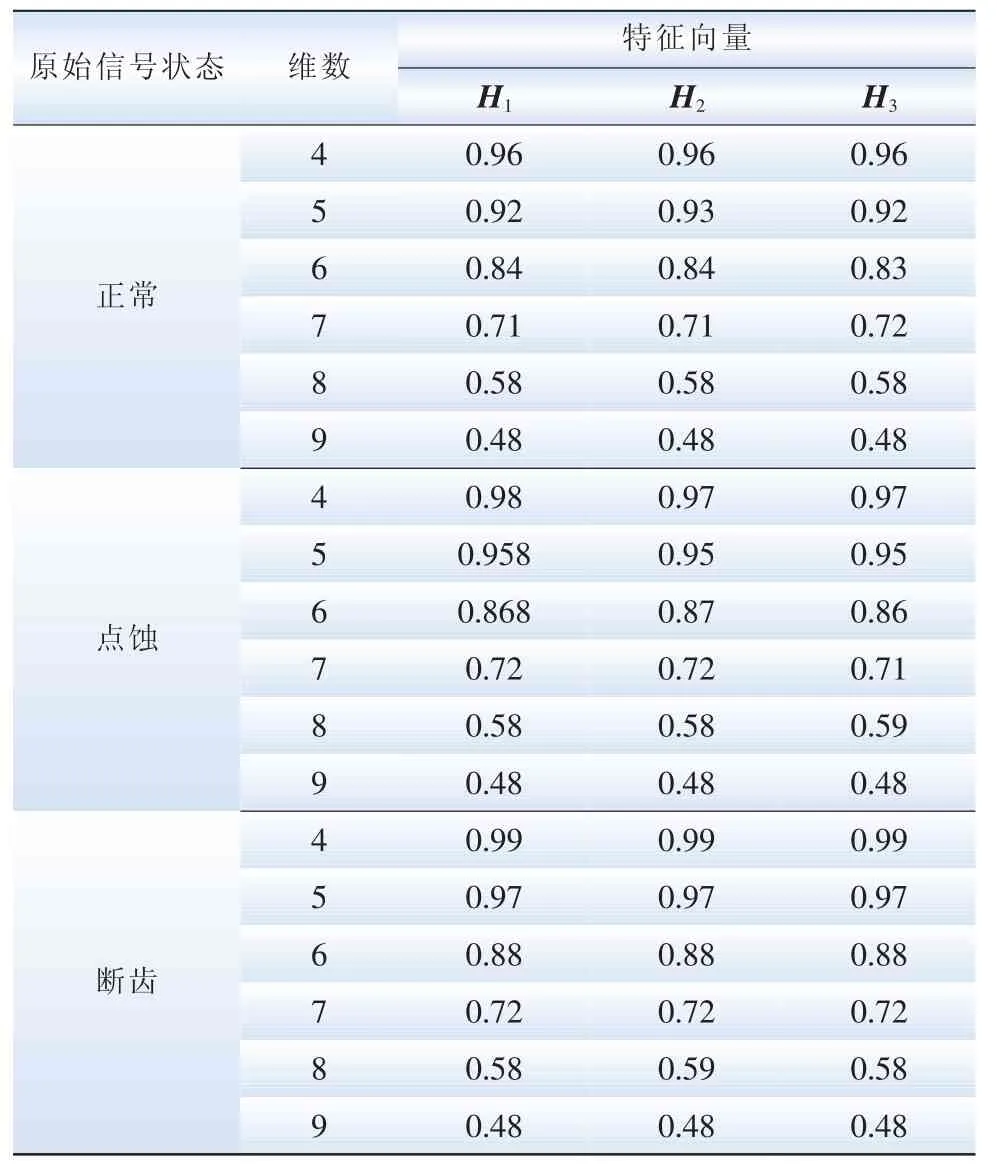
表1 齿轮箱振动信号的特征向量Table 1 The characteristic vector of the gear box vibration signal

3.2 诊断结果与分析

对齿轮箱正常、点蚀和断齿3种状态下各30组特征向量，从中选取15组作为训练样本，另15组作为测试样本，共45组训练样本和45组测试样本。将训练样本和测试样本输入到本文建立的基于遗传算法优化SVM的故障诊断模型中，进行风力发电机组齿轮箱故障模式的识别与诊断，诊断结果如表2所示。

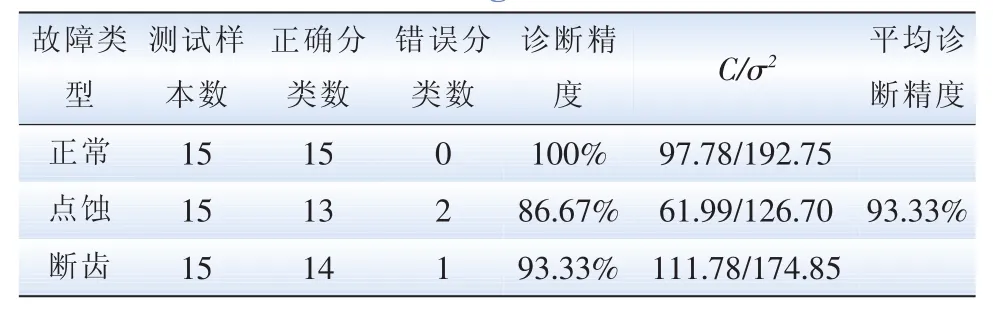
表2 故障诊断结果表Tab.2 Fault diagnosis results table

对于大齿轮正常时的状态诊断精度为100%，既能够完全识别齿轮正常时的状态；对于大齿轮断齿时的故障，第15组样本误诊断为点蚀故障，出现了错误分类；对于大齿轮点蚀故障，第3组和第6组样本误诊断为断齿故障，出现两组样本错误分类。分析其原因，可能是由于齿轮箱运行工况复杂，信号中含有大量噪声干扰，使得在提取大齿轮断齿和点蚀故障信号的特征向量时存在误差，影响了故障诊断的准确率。但是，本文提出的基于多尺度排列熵和基于遗传算法优化SVM相结合的故障诊断方法，平均诊断精度达93.33%，具有较高的故障诊断精度，能够有效识别风力发电机组齿轮箱的故障状态。

4 总结

针对风力发电机组齿轮箱非线性、非平稳信号难以检测的难题，本文提出了基于多尺度排列熵和支持向量机的故障诊断方法，并通过对风力发电机组齿轮箱实验数据的仿真分析，可得出以下结论：

1）根据多尺度排列熵提取齿轮箱在3种状态下的特征向量可以看出，3种状态类型的的特征向量存在明显的差异，大齿轮在断齿时的值最大，正常时的值最小，说明多尺度排列熵能够有效提取信号的特征向量，为后续故障模式的识别与分类奠定了基础；

2）根据齿轮箱故障诊断结果可以看出，在小样本条件下，基于遗传算法优化SVM的诊断模型依旧能够进行齿轮箱故障模式的识别与分类，且诊断精度较高，说明该方法能够较理想地区分故障类型；

3）本文提出的基于多尺度排列熵和支持相量机的故障诊断方法，诊断效果较为理想，为风力发电机组齿轮箱的故障诊断提供了一种新思路。

[1]PAUL A，WOERMAN M.Modeling a clean energy standard for electricity：policy design implications for emissions，supply，prices，and regions[C]//Resources For the Future，2011：108-124.

[2]AHMED N A，CAMERON M.The challenges and possible solutions of horizontal axis wind turbines as a clean energy solution for the future[J].Renewable&Sustainable Energy Reviews，2014，38（5）：439-460.

[3]龙泉，刘永前，杨勇平.基于粒子群优化BP神经网络的风电机组齿轮箱故障诊断方法[J].太阳能学报，2012，3（1）：120-125.LONG Quan，LIU Yongqian，YANG Yongping.Fault diagnosis method of wind turbine gear box based on BP neural network trained by particle swarm optimization algoritthm[J].Acta Energiae Solaris Sinica，2012，3（1）：120-125（in Chinese）.

[4] JIANG Y，TANG B，QIN Y，et al.Feature extraction method of wind turbine based on adaptive Monet wavelet and SVD[J].Renewable Energy，2011，36（8）：2146-2153.

[5]罗毅，甄立敬.基于小波包与倒频谱分析的风电机组齿轮箱齿轮裂纹诊断方法[J].振动与冲击，2015，34（3）：210-214.LUO Yi，ZHEN Lijing.Diagnosis method of turbine gearbox gearcrack based on wavelet packet and cestrum analysis[J].Journal of Vibration and Shock，2015，34（3）：210-214（in Chinese）.

[6]王军辉，贾嵘，谭泊.基于EEMD和模糊C均值聚类的风电机组齿轮箱故障诊断[J].太阳能学报，2015，36（2）：319-324.WANG Junhui，JIA Rong，TAN Bo.Fault diagnosis of wind turbine’s gearbox based on EEMD and fuzzzya cmeans clustering[J].Acta Energiae Solaris Sinica，2015，36（2）：319-324（in Chinese）.

[7]李海平，赵建民，宋文渊.基于EMD-EDT的行星齿轮箱特征提取及状态识别方法研究[J].振动与冲击，2016，35（3）：48-54.LI Haiping，ZHAO Jianmin，SONG Wenyuan.Method of planetary gearbox feature extraction and condition recognition based on EMD and EDT[J].Journal of Vibration and Shock，2016，35（3）：48-54（in Chinese）.

[8]李辉，郑海起，杨绍普.基于EMD和Teager能量算子的轴承故障诊断研究[J].振动与冲击，2008，27（10）：15-17.LI Hui， ZHENG Haiqi， YANG Shaopu.Research on bearing fault diagnosis based on EMD and teager energy operator[J].Journal of Vibration and Shock，2008，27（10）：15-17（in Chinese）.

[9]冯辅周，饶国强，司爱威，等.排列熵算法研究及其在振动信号突变检测中的应用[J].振动工程学报，2012，25（2）：221-224.FENG Fuzhou，RAO Guoqiang，SI Aiwei，et al.Research and application of the arithmetic of PE intesting the sudden change of vibration signal[J].Journal of Vibration Engineering，2012，25（2）：221-224（in Chinese）.

[10]冯辅周，饶国强，张丽霞，等.基于EMD和排列熵的轴承异常检测方法研究[J].轴承，2013（2）：53-56.FENG Fuzhou，RAO Guoqiang，ZHANG Lixia，et al.Research on abnormality detection method for bearings based on EMD and permutation entropy[J].Bearing，2013（2）：53-56（in Chinese）.

[11]梅杰，陈定方，李文锋，等.基于神经网络的多级行星齿轮箱故障诊断专家系统[J].中国工程机械学报，2011，9（1）：117-121.MEI Jie，CHEN Dingfang，LI Wenfeng et al.Fault diagnosis expert system of multi-stage planetary gearbox based on neural network[J].China Civil Engineering Journal，2011，9（1）：117-121（in Chinese）.

[12]焦振毅，任建文，陈鹏.基于模糊理论的变压器故障诊断模型研究[J].电力科学与工程，2012，28（6）：39-43.JIAO Zhenyi， REN Jianwen， CHEN Peng.Study on transformer fault diagnosis model based on fuzzy theory[J].2012，28（6）：39-43（in Chinese）.

[13]尹浩霖，基于小波分析和神经网络的风力发电机组故障诊断[D].西安：西安理工大学，2014.

[14]刘迎.基于SVM风电机组齿轮箱故障诊断系统研究[D].北京：华北电力大学，2013.

[15]贾峰.分形与排列熵在滚动轴承故障诊断中的应用[D].太原：太原理工大学，2014.

[16]何洋洋，贾嵘，李辉，等.基于随机共振和多尺度排列熵的水电机组振动故障诊断 [J].水力发电学报，2015，34（12）：123-130.HE Yangyang，JIA Rong，LI Hui，et al.Vibration fault diagnosis of hydroelectric generating set based on stochastic resonance and multidimensional permutation entropy[J].Journal of Hydrodynamics，2015，34（12）：123-130（in Chinese）.

[17]徐强.风电机组传动链状态诊断方法研究[D].北京：华北电力大学，2015.

[18]秦波，杨云中，陈敏，等.基于两类特征和最小二乘支持向量机的齿轮故障诊断方法[J].机械传动，2016（6）：126-131.QIN Bo，YANG Yunzhong，CHEN Min，et al.Gear fault diagnosis method based on two kinds of characteristic and least squares support vector machines[J].Mechanical transmission，2016（6）：126-131（in Chinese）.

[19]李赢，舒乃秋.基于模糊聚类和完全二又树支持向量机的变压器故障诊断[J].电工技术学报，2016，31（4）：64-70.LI YING，SHU Naiqiu.Transformer fault diagnosis based on fuzzy clustering and completely second tree support vector machine[J].Journal of Electrotechnical Society，2016，31（4）：64-70（in Chinese）.

Vibration Fault Diagnosis of Wind Turbine's Gearbox Based on Multidimensional Permutation Entropy and SVM

LIU Li1，JIA Rong1，LI Taotao1，YIN Haolin2，MA Xiping3，GUO Zewei1
（1.Xi’an University of Technology，Xi’an 710048，Shaanxi，China；2.China Hydropower Consulting Group Investment Co.，Ltd.，Beijing 100101，China；3.State Grid Gansu Electric Power Research Institute，Lanzhou 730050，Gansu，China）

Aiming at the problem that with the traditional method it is difficult to accurately detect the non-linear and non-stationary vibration signals of the wind turbine’s gearbox and the existing fault diagnosis methods can not effectively diagnose the early fault of the gearbox，this paper firstly introduces the permutation entropy algorithm to analyze the early fault of the gearbox vibration signal and then the multi-dimension permutation entropy algorithm to realize the feature extraction of the original vibration signal，so as to get the sample data of the fault diagnosis.Finally，the sample data is input into the diagnosis model based on genetic algorithm optimization support vector machine to complete the fault pattern recognition and diagnosis.The simulation results show that the method can effectively identify the abnormal working conditions of the gear box with high fault diagnosis accuracy.

gearbox；multi-dimension permutation entropy；genetic algorithm；support vector machine；fault diagnosis

2016-08-14。

刘 骊（1990—），男，硕士研究生，研究方向为电力系统新能源；

（编辑 李沈）

1674-3814（2017）05-0087-05

TM614

A

国家电网科技项目（522722150012）；陕西水利科技计划项目（2015s1kj-04）。

Project Supported by the Science and Technology Program of State Grid Cooperation of China（522722150012）；Shaanxi Water Conservancy Science and Technology Program（2015s1kj-04）.

贾 嵘（1971—），男，博士，教授，博士生导师，主要研究方向为电力系统自动化。