一些解析函数空间上积分算子的范数
2017-07-31罗家平
罗家平,文 邮
(嘉应学院数学学院 广东 梅州 514015)
一些解析函数空间上积分算子的范数
罗家平,文 邮
(嘉应学院数学学院 广东 梅州 514015)
若f是单位圆盘D上的解析函数,Volterra积分算子定义如下:
文章给出了Jg在不同的解析函数空间上的范数计算.
范数;积分算子;解析函数空间
1 引言
令D={z:z<1}是复平面C上的单位圆盘.H(D)表示单位圆盘D上的解析函数.定义1.1当0<p<∞,若对f∈H(D),且满足

定义1.2当α>0,α-Bloch空间记为Bα.若f∈H(D),Bα空间由满足下列条件的函数组成:
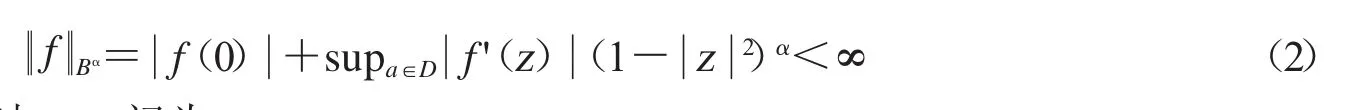
特别地,当α=1时,Bα记为B.
定义1.3当0≤s<∞,0<p<∞.若f∈H(D)且满足
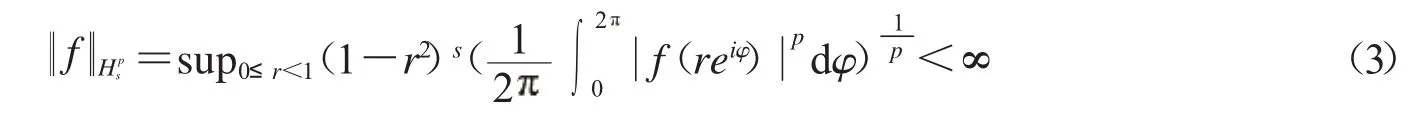
则称f属于Hp.H∞称为Bers-型空间,对f∈H∞,有

对空间H∞s赋予范数H∞,则H∞s为巴拿赫空间.
定义1.4当0≤p<∞,若f∈H(D)且满足f'∈Hp,该空间记为Sp.对Sp赋予以下范数

则Sp为巴拿赫空间.
定义1.5当-1<α<∞,若f∈H(D)且满足

则称f属于Dα.
定义1.6假设g∶D→C1是全纯映射且h∈H(D).积分算子Jg也称为Volterra型算子定义如下:

定义1.7若T为解析函数空间上的算子,T的范数为

Pommerenke在文献[11]中证明积分算子Jg在Hardy空间上有界性的充要条件;Bergman空间上积分算子Jg有界性的充要条件见文献[2-3];关于积分算子Jg的其他结论可见文献[1-4,6-10].在本论文中,讨论了积分算子Jg在不同的解析函数空间上范数的估计.
2 主要结论与证明
在这一节中,将给出主要结论与证明.结论的证明需要用到下面的引理.

首先给出Jg从Hα∞到Bα的范数,结论如下:
定理2.2设0≤α<∞.如果g∈H(D),积分算子Jg从到Bα有界的充分必要条件是supz∈D.进一步,有.

因此

反之,记c=supz∈Dg('z).对任意ε>0,存在z1∈D,使得g('z1)>c-ε.令
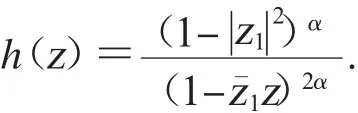
很容易验证h∈Hα∞且hH∞=1.又由
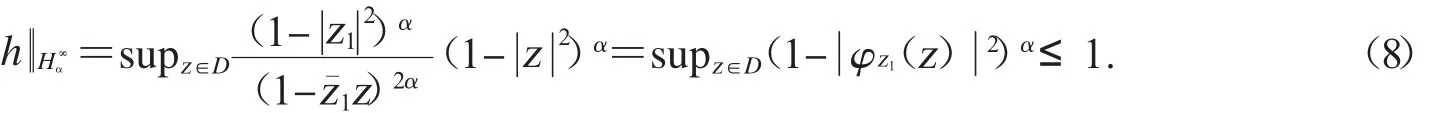
和
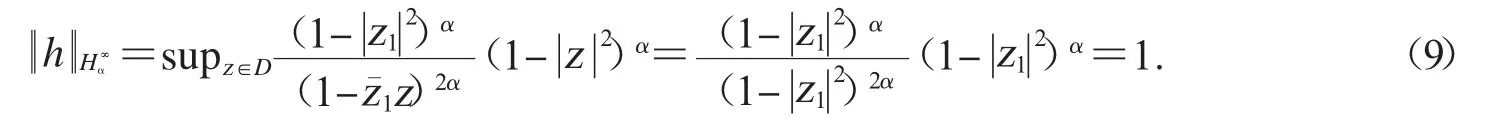

由ε的任意性,可得

由(7)和(11)可得结论.证毕.
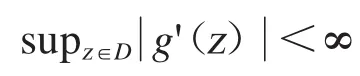
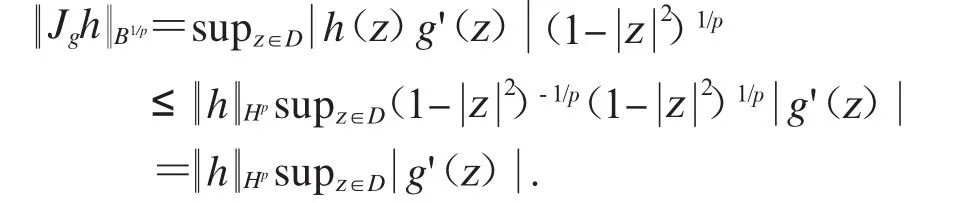
因此

反之,记c=supz∈Dg('z).对任意ε>0,存在z1∈D,使得g('z1)>c-ε.令

令z=reiθ,由Poisson积分方程可得

且有 h(z1)(1-z12)1/p=1,所以

由ε的任意性,可得

由(12)和(13)可得结论.证毕.
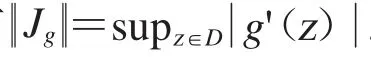
最后,给出Jg从H∞到其他解析函数空间上有界的范数,结论如下:
定理5下列结论成立:
(1)设-1<α<∞.如果g∈H(D),积分算子Jg从H∞到Dα有界的充分必要条件是supz∈Dg('z)<∞.进一步,有


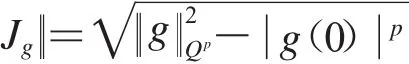
定理5的证明与文献[10]中的引理3.3类似,在此省略.
[1]ALEMAN A,CIMA J.An integral operator on Hpand Hardy’s inequality[J].Anal Math,2001,85(2):157-176.
[2]ALEMAN A,SISKAKISA.An integral operatoron Hp[J].Complex Variables,1995,28(2):140-158.
[3]ALEMAN A,SISKAKIS A.Integral operators on Bergman spaces[J].Indiana Univ Math J,1997,46(1):337-356.
[4]AUSTIN A.Multiplication and integral operators on Banach spaces of analytic functions[D].Hawaii:University of Hawaii,2010.
[5]DUREN P.Theory of HpSpaces[M].New York:Academic Press,1970.
[6]LI S,STEVIC S.Volterra-type operators on Zygmund spaces[J].J Ineq Appl,2007,312(2):1125-1134.
[7]LI S,STEVIC S.Generalized composition operators on Zygmund spaces and Bloch type spaces[J].J Math Anal Appl,2008,338(23):1282-1295.
[8]LI S,STEVIC S.Products of integral-type operators and composition operators between Bloch-type spaces[J].J Math Anal Appl,2009,34(3):596-610.
[9]LI S.On an integral type operator from the Bloch space into the QK(p,q)space[J].Filomat,2012,26(2):125-133.
[10]LIU J M,LOU Z J,XIONG C J.Essential norms of integral operators on spaces of analytic functions [J].Nonlinear Analysis,2012,75(2):5145-5156.
[11]POMMERENKE C.Schlichte funktionen and analytische funktionen von beschrankter mittlerer oszillation [J].Comment Math Helv,1977,52(3):591-602.
Norm of an Integral Operator on Some Analytic Function Spaces
LUO Jiaping,WEN You
(School of Mathematics,JiayingUniversity,Meizhou 514015,Guangdong,China)

norm;integral operator;analytic function spaces
TP391
A
1001-4217(2017)03-0042-04
2016-09-02
罗家平(1994—),女,汉族,研究方向为函数空间与算子理论.
基目项目:广东大学生科技创新培育专项资金(“攀登计划”专项资金)资助(pdjh20160465).
