分数Black-Scholes模型下美式亚式期权的近似定价法
2017-07-31林汉燕
林汉燕,袁 媛
(桂林航天工业学院理学部,广西 桂林,541004)
分数Black-Scholes模型下美式亚式期权的近似定价法
林汉燕,袁 媛
(桂林航天工业学院理学部,广西 桂林,541004)
在分数Black-Scholes模型下,首先应用偏微分方程法简要推导具有固定敲定价格的欧式几何平均亚式期权的定价公式,然后将标准Black-Scholes模型下美式期权定价的二次近似法推广到美式亚式期权,得到具有固定敲定价格的美式几何平均亚式期权价格的近似解析式.
分数Black-Scholes模型;美式亚式期权;几何平均;二次近似法
0引言
亚式期权是期权在到期日的收益依赖于整个有效期内标的资产价格平均值的合约.由于亚式期权是一种强路径依赖型期权,所以可以避免投机者通过操纵标的资产价格获得暴利;另一方面,由于亚式期权比标准期权便宜,而且随着时间增大,期权价格呈下降趋势,所以对于某些公司亚式期权比标准期权更有吸引力.目前亚式期权在国际贸易、基金公司、保险公司等金融领域应用广泛,很多学者对它的定价进行了研究[1-4],但这些成果都是针对标准Black-Scholes模型下的欧式亚式期权,美式亚式期权的研究很少.美式亚式期权是场内外交易的重要期权之一,由于它具有美式期权的特点,可以在到期日前提前实施,但何时实施获利最多未知,不能得到价格解的显示表达式;同时又具有亚式期权的特点,所以定价显得更复杂.目前美式亚式期权的研究成果有Ben-Ameur等用动态规划法研究美式亚式期权价格[5];Hanse等在标准Black-Scholes模型下研究具有浮动价格的算术平均和几何平均的美式亚式期权价格的定价[6];王旭等先利用Monte-Carlo模拟Black-Scholes模型下标的资产的价格路径,然后应用偏最小二乘回归法计算美式亚式期权价格[7];孔文涛等在标的资产价格服从跳跃-扩散模型、利率遵循短期随机利率模型的基础上,应用总体最小二乘拟蒙特卡罗方法为美式亚式期权定价[8]等.分数Black-Scholes模型[9]是比标准Black-Scholes模型更接近股票运动特征的模型.在分数Black-Scholes模型下,文献[10]用拟条件期望法得到了浮动价格的平均欧式亚式期权的定价公式;文献[11]给出了基于可靠性思想的期权定价方法;文献[12]应用保险精算法推导具有固定敲定价格的几何平均欧式亚式期权的定价公式;文献[13]应用随机分析理论讨论亚式期权的定价;文献[14]应用偏微分方程法研究亚式期权的定价.本文在分数Black-Scholes模型下,对连续情形下具有固定敲定价格的几何平均美式亚式期权的价格进行研究.为下文叙述方便,首先用偏微分方程方法[14]简要推导欧式几何平均亚式期权的定价公式.在这基础上,将标准Black-Scholes模型下美式期权定价的二次近似法[15]应用到美式亚式期权,得到期权价格的近似解析式.
1 基本模型
定义1设(Ω,F,R)是一个完备的概率空间,H∈(0,1),称连续的高斯过程BH={B(Ht);t≥0}是Hurst参数为H的分数布朗运动,如果它满足:
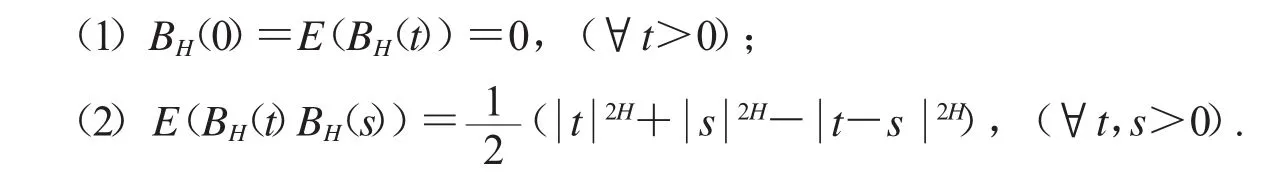
这里E表示关于概率测度P的期望.
分数布朗运动的另一个重要性质是具有自相似性,即对任意的H∈(0,1)和α>0,B(Hαt)与αHB(Ht)有相同的有限维概率分布.本文讨论Hurst参数1/2<H<1时的情形.
现假设金融市场仅有两种资产,资产交易的额度和时间连续,交易时间为[0,T],可以买空卖空,不存在交易税收和费用,借款和存款的利率相同.设第一种资产是连续支付红利的风险资产,其价格S=S(t)满足分数布朗运动:

第二种资产是无风险证券,其价格A(t)满足:

其中r(t)表示无风险利率,q(t)表示红利率,σ≠0表示股价瞬时波动率(常数),μ(t)表示股价期望回报率,B(Ht)表示分数布朗运动,“◇”表示Wick积分.模型(1)、(2)称为分数Black-Scholes模型,并且是无套利的完全市场模型.
文献[14]证明了分数Black-Scholes模型下连续情形的具有固定敲定价格的欧式几何平均亚式期权的价格F(t,J,S)满足:

2 欧式具有固定敲定价格的几何平均亚式期权的定价
定理1分数Black-Scholes模型下无风险率为r,红利率为q,波动率为σ(r、q、σ均为常数),到期时间为T,执行价格为K的具有固定敲定价格几何平均亚式看涨期权在时刻t的价格c(t,J,S)为


类似得
定理2分数Black-Scholes模型下无风险率为r,红利率为q,波动率为σ(r、q、σ均为常数),到期时间为T,执行价格为K的具有固定敲定价格几何平均亚式看跌期权在时刻t的价格p(t,J,S)为
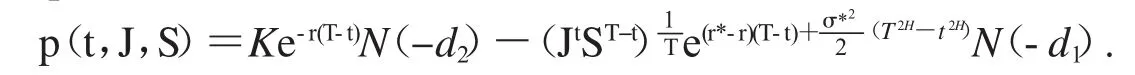
3 美式具有固定敲定价格的几何平均亚式期权的近似定价
设e(ξ,t)=e(t,J,S)(ξ同前)为t时刻美式亚式看涨期权价格的提前实施溢价,则e(ξ,t)=U(ξ,t)-u(ξ,t),其中U(ξ,t)=C(t,J,S)、u(ξ,t)=c(t,J,S)分别为t时刻美式亚式看涨期权和欧式亚式看涨期权价格.U(ξ,t)适合定解问题

其中0<ξ<ξ*,0<t<T,ξ*表示美式亚式看涨期权的最佳实施边界.显然e(ξ,t)满足方程

令e(ξ,t)=h(φ)g(ξ,h(φ)),其中h=h(φ)、φ=φ(t)待定,且φ(t)满足φ(T)=0,上式可化为


由此得
定理3分数Black-Scholes模型下无风险率为r,红利率为q,波动率为σ(r、q、σ均为常数),到期时间为T,执行价格为K的具有固定敲定价格几何平均美式亚式看涨期权在t时刻价格C(t,J,S)为

类似得
定理4分数Black-Scholes模型下无风险率为r,红利率为q,波动率为σ(r、q、σ均为常数),到期时间为T,执行价格为K的具有固定敲定价格几何平均美式亚式看跌期权在t时刻价格P(t,J,S)为
4 结论
本文在分数Black-Scholes模型下用二次近似法推导了连续情形的具有固定敲定价格美式亚式期权定价的近似公式.公式形式与Black-Scholes模型下标准美式期权定价的近似公式相似.
[1]戴民.路径依赖期权二叉树方法的数值分析[D].上海:复旦大学,2002.
[2]姜礼尚.期权定价的数学模型和方法[M].北京:高等教育出版社,2003.
[3]周清,李超.分数Vasicek利率模型下几何平均亚式期权的定价公式[J].应用数学学报,2014,37(4):662-675.
[4]CAO G L,WANG Y.Risk-neutral pricingforgeometric average Asian option with floatingstrike[J].Journal of University of Chinese Academy of Sciences,2015,32(1):13-17.
[5]BEN-AMEURH,BRETONM,L'ECUYERP.Adynamicprogramming procedure for pricing American-style Asian option[J].Management Science,2002,48(5):625-643.
[6]HANSEN A T,JORGENSEN P L.Analytical valuation of American-style Asian option[J].Management Science,2000,46(8):1116-1136.
[7]王旭,王拉省.偏最小二乘回归在美式-亚式期权定价中的应用[J].纺织高校基础科学学报,2008,21(1):24-130.
[8]孔文涛,张卫国.带跳市场中随机利率下的美式-亚式期权定价[J].系统工程学报,2012,27(3):338-342.
[9]ANDELBROTB.Long-runlinearity,locallyGaussianProcesses-spectraand infinity variance[J].International Economic Review,1969,10(1):2-111.
[10]沈明轩,何朝林.分数布朗运动环境中几何平均亚式期权的定价[J].山东大学学报理学版,2013,48(3):48-52.
[11]孙玉东,师义民,谭伟.分数布朗运动环境下亚式期权定价的新方法[J].工程数学学报,2012,2(2):173-178.
[12]周银,杜雪樵.分数布朗运动下的亚式期权定价[J].合肥工业大学学报(科学版),2011,34(2):317-320.
[13]裴晓芬,冯德成.分数布朗运动下带红利的亚式期权定价的新解法[J].河北师范大学学报(自然科学版),2014,38(2):123-128.
[14]武文娜,周圣武,黎伟.分数布朗运动下支付红利的亚式期权定价[J].河南科技大学学报(自然科学版),2012,33(4):100-104.
[15]BARONE-ADESIG,WHALEY R E.Efficientanalytic approximation of American option values[J].The Journal of Finance,1987,42(2):301-320.
American-Style Asian Option Pricing in the Fractional Black-Scholes Model
LIN Hanyan,YUAN Yuan
(Guilin Universityof Aerospace Technology,Facultyof Science,Guilin 541004,Guangxi,China)
The formulas of the European-style geometric average Asian option with fix strike price by partial differential equation method in the fractional Black-Scholes model are derived. Based on the formulas,the classical quadratic approximation in the standard Black-Scholes model is applied to the pricing of American-style Asian option.The approximate formulas of American-style geometric average Asian option with fix strike price are obtained.
fractional Black-Scholes model;American-style Asian option;geometric average; quadratic approximation
O211.6;F830.9
A
1001-4217(2017)03-0015-07
2016-09-02
林汉燕(1973—),女,汉族,广西贵港人,硕士,副教授,研究方向:金融数学. E-mail:linhanyan2006@163.com
广西教育厅科研项目(YB2014436).
