高压调控的磁性量子临界点和非常规超导电性∗
2017-07-31程金光
程金光
(中国科学院物理研究所,极端条件物理重点实验室,北京 100190)(2016年11月2日收到;2016年11月19日收到修改稿)
专题:高压下物质的新结构与新性质研究进展
高压调控的磁性量子临界点和非常规超导电性∗
程金光†
(中国科学院物理研究所,极端条件物理重点实验室,北京 100190)(2016年11月2日收到;2016年11月19日收到修改稿)
通过化学掺杂或者施加高压等调控手段抑制长程磁有序可以实现磁性量子临界点,在其附近往往伴随出现诸如非费米液体行为或者非常规超导电性等奇特物理现象.相比于化学掺杂,高压调控具有不引入晶格无序和精细调控等优点.利用能提供良好静水压环境的立方六面砧和活塞-圆筒高压低温测量装置,首先系统研究了具有双螺旋磁有序结构的CrAs和MnP单晶的高压电输运行为,分别在Pc≈0.8 GPa和8 GPa实现了它们的磁性量子临界点,并在Pc附近分别观察到Tc=2 K和1 K的超导电性,相继实现了铬基和锰基化合物超导体零的突破;然后,详细测量了FeSe单晶高压下的电阻率和交流磁化率,绘制了详尽的温度-压力相图,揭示了电子向列序、长程反铁磁序和超导相之间的相互竞争关系,特别是在接近磁有序消失的临界点Pc≈6 GPa附近观察到Tmaxc=38.5 K的高温超导电性,表明临界反铁磁涨落对FeSe中的高温超导电性起重要作用.
高压调控,磁性量子临界点,非常规超导,非费米液体行为
1 引 言
近年来,量子临界性被认为是强关联电子体系中许多反常物理现象的普适性特征而备受关注[1,2].对于目前已知的非常规超导体系[3−6],包括重费米子和有机化合物超导体、铜基和铁基高温超导体等,它们的超导相图都可以在量子临界的框架下得到统一的理解,即超导电性往往出现在反铁磁序消失的临界点附近.实验上,利用化学掺杂或者施加高压等调控手段,将发生在有限温度的连续相变(通常为反铁磁序)抑制到绝对零度附近,就可以实现量子临界点,如图1所示.虽然量子临界点是发生在零温的电子相变,但是与之相关的量子临界涨落可以在非常大的温度范围内影响物理性质,造成一系列奇特的物理现象.例如,描述正常金属中低温电子合作行为的朗道费米液体理论往往会失效,取而代之的是一系列反常的非费米液体行为和电子有效质量的显著增加[7],对这些反常现象的描述超越了朗道费米液体理论框架.此外,由于量子临界点附近的超导电性与长程反铁磁序毗邻,人们普遍认为反铁磁临界涨落是造成电子配对的重要机理,支持非常规超导[5].因此,探索并实现磁性量子临界点不仅可以系统地揭示反常物理行为的规律,为发展新颖的理论框架提供机遇,而且还可能发现非常规超导电性,从而为探索新型的非常规超导体系提供重要的思路.
尽管化学掺杂是抑制长程磁有序进而诱导非常规超导电性常用的手段,然而高压调控具有独特的优势:一方面,施加物理压力原则上不会引入晶格无序、造成相分离或者提供额外的电荷载流子,因此是一种相对“干净”和“均匀”的调控手段,有利于揭示材料内禀性质的演化过程;另一方面,通过非常小步长的增加压力还可以实现精确的物性调控,从而以“可控”的方式趋近量子临界点并详细研究临界区域非常窄范围内的奇异物理性质,这一点在许多重费米子体系中尤为重要[3].
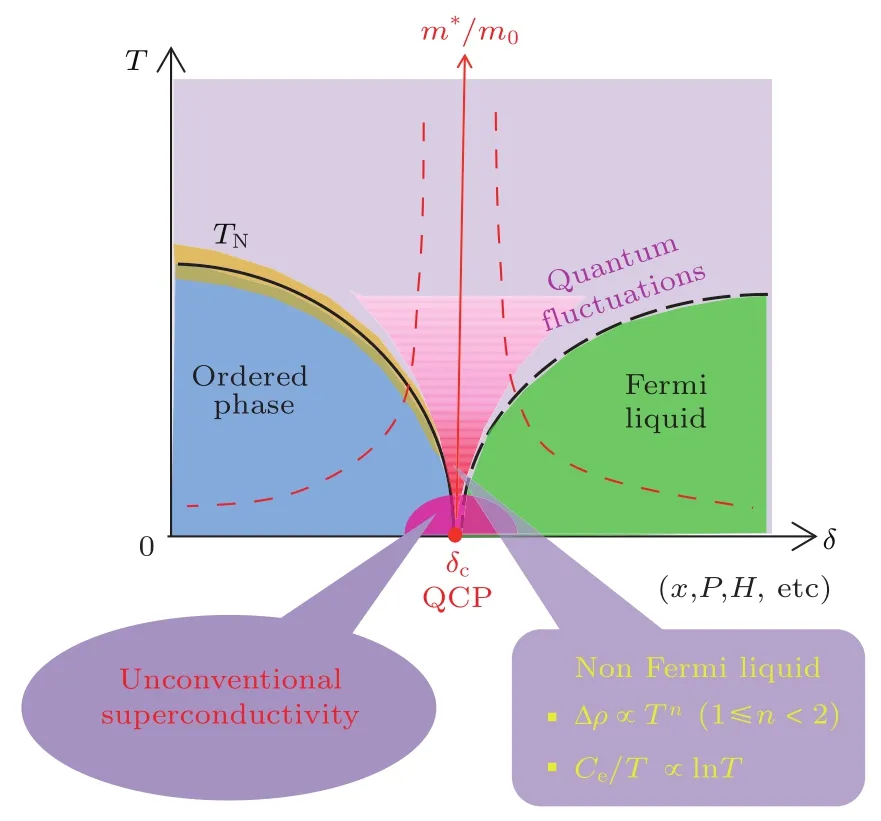
图1 量子临界点示意图 通过化学掺杂x、施加高压P或者磁场H等调控手段δ将发生在有限温度TN的有序相变抑制到零温附近,就可以实现量子临界点(QCP),在临界点δc附近往往发现奇特的物理现象,例如非费米液体行为、电子有效质量m∗/m0的显著提高,甚至非常规超导电性Fig.1.Aschematic drawing of quantumcritical point(QCP),which arises when a continuous phase transition at TNis suppressed tooccur at zerotemperature by the application of ex ternal tuning parameterδ,such as the chemical doping x,pressure P,ormagnetic field H.Exotic phenomena such as the non-Fermi-liquid behaviors,a d ramatic enhancement of the eff ective mass m∗/m0,and unconventional superconductivity are frequently observed near the QCP.
值得注意的是,近年来越来越多的高压实验研究表明,保持良好的静水压环境是高压物性测量中获得材料本征压力效应的关键[8−10].很典型的一个例子是CaFe2As2,能否利用高压诱导其出现超导电性完全取决于静水压的好坏[8].采用气体或者液体传压介质的高压技术通常能提供相对较好的静水压环境.目前,在测量高压下的电输运性质时,能提供较好静水压环境的高压技术主要有活塞-圆筒[11]和立方六面砧压腔[12].前者能提供约3 GPa的最高压强,是目前已经商业化的、应用较广泛的高压技术,本文中将不再赘述;后者能实现高达16 GPa的压强[13],样品空间较大,操作相对简易,在本文第二部分将详细介绍.近年来,基于金刚石对顶砧[14]的高压电输运测量技术得到迅速推广,其优点是能实现100 GPa以上的超高压,而且高压装置体积小,因而容易与商用恒温器和磁体配合使用,但是由于样品空间的制约通常采用固体传压介质,这不可避免地会造成较大的压力不均匀性(例如,单轴压力和切向应力等)[15].
本文概述近三年来我们利用活塞-圆筒和六面砧高压技术探索压力诱导的磁性量子临界点和非常规超导电性方面的最新研究进展[16−18].第二部分介绍在中国科学院物理研究所建立的国内第一台基于立方六面砧压腔的高压低温物性测量装置;第三和第四部分分别介绍利用高压抑制双螺旋磁体CrAs和MnP的长程磁有序,并在它们的磁性量子临界点附近首次发现超导电性;第五部分将给出FeSe单晶的完整温度-压力相图,揭示电子向列序、反铁磁序与高温超导的相互竞争关系;第六部分是结论和展望.
2 立方六面砧高压低温物性测量装置
基于立方六面砧压腔的高压-低温物性测量技术起源于日本东京大学物性研究所,由Mori教授等[19]在20世纪90年代设计并逐步发展起来.如图2(a)所示,其核心部件由六个压砧构成,通过一对对称的具有45◦斜面的导向块将这六个压砧向中心推动来同步挤压固体密封块,密封块中心放置了聚四氟乙烯胶囊,样品悬挂在充满液体传压介质的胶囊中.这种三轴加压和样品浸泡在液体传压介质中的方式能保证良好的静水压环境,即压力的各向同性和均匀性[12].然而由于高压腔体积庞大,实现低温时需要消耗大量的液氮和液氦低温制冷剂(例如,从室温降至2 K需30 L以上的液氦),这成为阻碍此技术推广的一个重要原因.Mori教授的继任者Uwatoko教授进一步发展了此技术,在2008年设计了一种微型立方六面砧压腔[20],在保持最高压强不变的情况下大大缩小了高压腔体的体积,不仅大大降低了低温实验成本,而且更容易与极低温和强磁场等综合极端条件相结合[21].
我们在2014年将此技术引进到中国科学院物理研究所极端条件物理重点实验室,成功搭建了国内第一套基于立方六面砧的大腔体高压低温物性测量装置.如图2(b)所示,此装置将微型六面砧压腔、交换气体型恒温器和室温孔超导磁体集成在一起,实现了最高压强Pmax=15 GPa、最低温度Tmin=1.4 K和最高磁场Hmax=9 T等综合极端条件下的物性测量,包括电阻率、磁阻、霍尔电阻、交流磁化率、交流比热等.最近,我们与人民大学于伟强教授课题组合作,成功地将此装置应用于高压下的核磁共振测量,详细研究了FeSe单晶在高达8 GPa下的微观磁性,获得了有意义的结果.因此,基于立方六面砧的高压低温物性测量装置将成为获得10 GPa量级静水压下高压效应的重要研究手段.

图2 (a)立方六面砧装置的加压示意图,其中六个压砧同步挤压中心的立方密封块,样品放置在密封块中心充满液体传压介质的聚四氟乙烯胶囊中;(b)中国科学院物理研究所搭建的基于立方六面砧压腔的高压低温物性测量装置,包括六面砧高压腔、气体交换腔恒温器和超导磁体,可实现最高压强Pmax=15 GPa、最低温度Tmin=1.4 K和最高磁场Hmax=9 T的综合极端条件Fig.2.(a)Aschematic d rawing of the cubic anvil cell(CAC)consisting of six anvils converging ontothe cubic gasket,in which the sample was suspended in a Tefl on cell fi lled with the liquid pressu re transmittingmed ium;(b)a picture of the CAC apparatus estab lished in the IOP CAS by integrating the CAC with the L-Heliumcryostat and a superconducting magnet.This systemenab les us tomeasure physical properties under mu ltiple ex treme conditions including the Pmax=15 GPa,Tmin=1.4 Kand Hmax=9 T.
3 CrAs中高压诱导超导电性的发现[16]
在常温常压条件下,CrAs具有MnP型(B31)正交晶体结构,如图3(a)插图所示,晶格参数为a=5.649Å,b=3.464Å,c=6.2084Å(空间群Pnma).常压下随着温度降低,CrAs在TN≈265 K发生一级反铁磁相变[22−24],中子粉末衍射表明其在TN以下具有双螺旋型的反铁磁结构,Cr离子的磁矩约为1.7µB,在ab平面内旋转,螺旋传播方向为c轴.很奇特的是,伴随着反铁磁转变,其晶体结构在TN处发生强烈的等结构变化,特别是b轴突然膨胀约4%,而a和c轴分别突然缩短约0.3%和0.9%,造成体积膨胀约1%.虽然在铁基超导体的母体化合物中,反铁磁(自旋密度波)转变的同时也伴随着结构相变,即从四方到正交晶体结构的变化,不同的是CrAs在TN处发生的是等结构变化,晶体结构的对称性并没有降低.对高质量CrAs单晶的电阻率测试表明[25],其在室温以下的整个温区表现出良好的金属性电导,电阻率和磁化率在一级反铁磁转变处都呈现突然跳变,升降温时TN存在约10 K的热滞.通常情况下,这种与结构变化紧密关联的磁相变往往对压力是非常敏感的.早期对CrAs多晶的高压电阻率测试确实表明[26],TN随着压力的升高而逐渐降低,在约5 kbar(1 bar=105Pa)时就消失了,这意味着高压可能在CrAs中诱导磁性量子临界点.然而,早期的高压研究并没有关注临界点附近的低温物性.
从2013年6月开始,我们利用活塞-圆筒高压腔对高质量的CrAs单晶[25]开展了仔细的高压电阻率和磁化率测试,最终在其磁有序被压制的临界点附近首次观察到超导电性[16].图3(a)显示的是0≤P≤7 kbar范围内CrAs单晶在整个温区的ρ(T)曲线.从图3(a)可以清晰地看到:TN随着压力的增加逐渐向低温移动,6.97 kbar时已降至约70 K;当P > 7 kbar时,从ρ(T)曲线上已经看不出明显反常,这意味着高压已经完全抑制了反铁磁序.值得注意的是,当P<3 kbar时,ρ(T)表现出与常压类似的强烈一级相变特征;而当P>3 kbar时,ρ(T)在TN处则表现为相对平滑的拐点,而且随着压力的增加越来越弱,但是升、降温时TN处仍然存在较大热滞,表明其一级相变的特征仍然维持.上述结果与早期的高压研究[26]类似,证实了高压确实可以完全抑制长程磁有序.图3(b)和图3(c)显示了不同压力下的低温ρ(T)数据,证实了磁性量子临界点附近确实出现了超导电性.可以看出,CrAs的ρ(T)在常压下降到0.3 K也没有任何超导迹象;在0< P < 3 kbar区间,当高温ρ(T)在TN处表现为突然跳变时,虽然低温ρ(T)在T<3 K出现多台阶的下降,但是并没有达到零电阻;在3<P<7 kbar区间,当高温ρ(T)在TN处表现为相对平滑的拐点时,低温ρ(T)经过多台阶的下降,最终在约1 K达到零电阻,表明实现了超导电性,而这种多台阶式的ρ(T)下降归因于反铁磁相与超导相的共存;当P>7 kbar时,反铁磁序完全消失,超导转变表现为非常陡峭的下降,约11 kbar时的超导转变温度为Tc=1.5 K(本文中定义达到零电阻的温度为超导转变温度);当P>11 kbar时,Tc随着压力的增加而逐渐降低.我们还测试了高压下的交流磁化率,进一步确认了P>8 kbar以上的超导相占样品体积的90%以上,证实为体超导.而且,在3<P<7 kbar之间超导体积因子逐渐增加,也印证了超导相与反铁磁相是共存的,与ρ(T)中观察到的多台阶下降一致.
根据上述测试结果,我们绘制了CrAs单晶的温度-压力相图.如图4(a)所示,随着压力升高,TN逐渐降低,外推至零温的临界压强Pc≈8 kbar.如图4(b)所示,在3 kbar<P<Pc区间,超导相与反铁磁相共存,造成超导转变温度宽度∆Tc(定义为电阻率下降10%和90%的温度范围)较大(约1 K),超导相的抗磁体积因子|4πχ|随压力的升高而逐渐增加;最终当P > Pc时,|4πχ|超过90%且保持恒定,而且∆Tc小于0.1 K,表明进入体超导态;Tc在11 kbar附近呈现出较宽的极大值,然后随压力的升高逐渐缓慢降低.
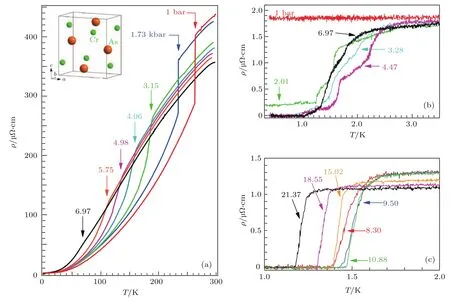
图3 (a)0≤P≤7 kbar范围内CrAs单晶在整个温区的电阻率ρ(T)数据,图中数值表示压强,单位为kbar,箭头指示反铁磁有序温度TN,从中可以清晰地看出压力逐渐抑制TN,插图为CrAs的晶体结构;(b),(c)0≤P≤21 kbar范围内CrAs单晶在低温区的ρ(T)数据,从中可以看出超导转变的演化过程[16]Fig.3.(a)Resistivityρ(T)of the C rAs single crystal under various hyd rostatic pressu res upto7 kbar in the whole temperatu re range high lighting the variation with pressu re of the antiferromagnetic transition temperature TNind icated by the arrows.Inset shows a schematic crystal structure of CrAs.(b)and(c)ρ(T)data at lowtemperatu res in the whole investigated pressu re range high lighting the evolu tion with pressu re of the superconducting transition[16].
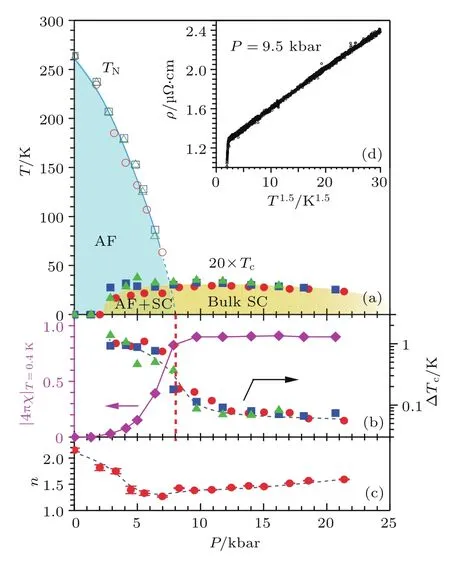
图4 (a)C rAs单晶的温度压力相图,其中AF和SC分别代表双螺旋反铁磁序和超导相;(b)从交流磁化率数据估计的0.4 K时的超导抗磁体积因子|4πχ|T=0.4K和10%—90%超导转变温度宽度∆Tc随压力的变化;(c)低温正常态电阻率温度指数n随压力的变化;(d)按照ρ-T1.5画出的P=9.5 kbar的正常态ρ(T),可以看到很好的线性关系;(a)—(c)中红色圆圈、蓝色方块和绿色三角符号分别代表三个不同样品测试的结果[16]Fig.4. (a)Temperature-pressu re phase d iagramof CrAs crystal. AF and SC represent the antiferromagnetismand superconductivity,respectively.Tchas been scaled by a factor of 20 for clarity. (b)The superconducting shielding fraction at 0.4 K,|4πχ|T=0.4K,and the superconducting transition temperatu re wid th,∆Tcas a function of pressu re.Here∆Tcis defined as the 10%–90%superconducting transition wid th.(c)Pressure dependence of the low-temperature resistivity exponent,n,obtained fromthe power-lawfi tting tothe normal-state resistivity below10 K.(d)Aplot ofρversus T1.5for the normal-stateρ(T)cu rve at P=9.5 kbar.The symbols of circle(red),square(b lue),and triangle(green)in(a),(b),(c)represent three independent samples with residual resistivity ratio=240,327,and 250,respectively[16].
CrAs的超导相图与前面提到的许多非常规超导体系的相图非常类似,包括圆顶状的Tc(P)曲线,这意味着近邻反铁磁序的临界涨落可能是造成超导配对的重要媒介.通过对CrAs正常态的低温电阻率拟合,即ρ(T)=ρ+ATn,发现电阻率的温度指数在3–20 kbar很宽的压力区间接近n=1.5±0.1,如图4(c)和图4(d)所示.这与三维反铁磁体系中由于磁涨落对准粒子的非相干散射给出的理论值非常接近,表明在Pc附近的反铁磁涨落对电输运性质具有重要影响.此外,Kotegawa等[27]对CrAs进行了高压核四极矩共振研究,发现1/(T1T)在Tc处并没有呈现出Bardeen-Cooper-Schrieff er常规超导体特有的Hebel-Slichter相干峰,进一步支持CrAs中观察到的超导态具有非常规配对机理.由于电子能带结构计算表明CrAs中费米面附近的电子态密度主要来源于Cr-3d电子[28],因此CrAs成为第一个铬基化合物超导体,从而启发人们探索新型的铬基非常规超导体.例如,浙江大学曹光旱教授课题组[29−31]合成了一类新型的准一维超导体A2Cr3As3(A=K,Rb,Cs),表现出反常高的上临界磁场µ0Hc2,成为最近强关联电子体系的一个研究热点.
4 MnP中高压诱导超导电性的发现[17]
在CrAs工作的基础上,我们继续对与CrAs具有相同晶体结构和类似双螺旋反铁磁基态的MnP单晶开展了详细的高压研究.在展示高压实验结果之前,我们首先对常压下的物理性质做简单介绍.在常温常压下,MnP也具有正交B31-型晶体结构,晶格常数为a=5.26Å,b=3.17Å,c=5.92Å.在不加外磁场情况下降温,MnP先后经历了两个磁相变[32,33]:首先,在TC≈290 K附近发生顺磁到铁磁转变,Mn3+磁矩沿着b轴平行排列,在低温时饱和磁矩达到约1.3µB/Mn;然后在Ts≈50 K从铁磁态转变为双螺旋反铁磁结构,类似于CrAs,Mn磁矩在ab平面内旋转,螺旋传播方向沿着c轴,但是螺旋的周期远大于CrAs.MnP在整个温区也具有金属性电导,电阻率ρ(T)在TC处表现出明显的拐点;而c-轴ρc(T)在Ts处出现台阶式跃变[34].因此,通过跟踪高压下电阻率曲线上的这些反常,我们就可以获得TC和Ts随压力的变化关系,从而探索磁性量子临界点和可能的超导电性.
图5(a)给出了0≤P≤10.7 GPa范围MnP单晶电阻率ρ(T).我们测量的MnP样品是采用Sn助溶剂法生长的高质量的针状单晶,电流方向沿着最长的b轴方向.高压电阻率测试采用的是立方六面砧压腔.从图5(a)可以清晰地看出,常压下的ρ(T)在铁磁相变TC=291 K具有明显拐点,对应图5(b)所示的dρ/d T曲线上的尖峰;当压力升高到2.8 GPa时,ρ(T)形状基本保持不变,只是TC降到约250 K;然而,当P=5.0 GPa时,ρ(T)和dρ/d T曲线都表现出显著不同的行为,前者在约200 K出现拐点,对应在dρ/d T曲线上的上跳,正如后面交流磁化率所示,这些不同的电阻率特征是由于铁磁相变在P>3 GPa时变为反铁磁相变造成的.因此,我们将P>3 GPa的磁有序转变温度定义为Tm.如图5(a)和图5(b)所示,随着压力的增加Tm逐渐降低,7.4 GPa时已降至约70 K.当P≥8.1 GPa时,ρ(T)上已经不能看出任何明显反常,这意味着高压已经完全抑制了长程磁有序.
值得一提的是,Banus[35]早在1972年就曾利用固体传压介质(AgCl)对MnP单晶开展过高压研究,发现其磁有序温度在3–5 GPa时不但没有降低反而随压力增加稍微升高,与我们看到的单调降低完全不同.这表明MnP磁有序相变的压力响应对静水压环境是非常敏感的.早期实验采用的固体传压介质造成的非静水压环境不利于抑制磁有序,而只有在较好的静水压条件下才能实现磁性量子临界点.通过这一对比可以凸显立方六面砧压腔的优势.

图5 (a),(b)0≤P≤10.7 GPa范围内MnP单晶在整个温区的电阻率ρ(T)和相应的温度导数dρ/d T,图中数值表示压强,单位为GPa,从中可以清晰看出压力逐渐抑制磁有序温度(竖直箭头指示);(c)0≤P≤1.07 GPa范围内的c-轴电阻率ρc(T),从中可以看出双螺旋反铁磁有序温度Ts随压力的变化;(d)不同压力下的交流磁化率χ′(T),从中可以看到新的反铁磁转变T∗[17]Fig.5.(a)Resistivityρ(T)and(b)the temperature derivative dρ/d Tof the MnP single crystal under various pressu resupto10.7GPa high lighting the variation with pressure of themagnetic transition indicated by the vertical arrows;(c)the c-axisρc(T)data at lowtemperatu res high lighting the evolution with pressure of the doub le helical transition at Ts;(d)temperature dependence of the ac magnetic susceptibility χ′(T)measured under various pressu res,which evidences the appearance of a newmagnetic transition at T∗[17].
为了跟踪Ts随压力的演化关系,我们还利用活塞-圆筒压腔测试了MnP单晶的c-轴ρc(T).如图5(c)所示,常压下ρc(T)在Ts处表现为小的台阶式跳跃;随着压力的升高Ts迅速向低温移动,在约1 GPa时完全消失.图5(d)显示了MnP单晶不同压力下的交流磁化率χ′(T),从中可以直接跟踪TC和Ts随压力的变化.常压下,χ′(T)分别在TC和Ts处出现上升和下降,中间的平台即对应铁磁有序区;与图5(a)中电阻率结果一致,TC和Ts均随压力的增加逐渐向低温移动,Ts在约1.4 GPa时完全消失.出乎意料的是,在 P=1.8 GPa时χ′(T)重新在T∗≈50 K出现下降,意味着出现了一个新的反铁磁转变,而且T∗随着压力的增加迅速向高温移动,最终在约3 GPa时与TC汇合,导致铁磁相完全被压制,取而代之的是新的反铁磁序,对应于图5(a)中P>3 GPa电阻率曲线上的Tm.最新的高压中子衍射[36]、核磁共振[37],µ子自旋旋转(µSR)[38]和磁性X射线衍射[39]表明,高压下出现的新的反铁磁相仍然具有螺旋磁有序结构,不过与低压时T<Ts的螺旋磁有序结构有差别.
通过上述详细的高压下电阻率和交流磁化率测量,我们可以看到高压可以完全抑制MnP的长程磁有序,在Pc≈8 GPa实现磁性量子临界点.为了详细研究Pc附近的极低温性质,我们采用体积较小的对顶砧式高压腔与稀释制冷机配合,并采用氩气作为传压介质,尽量保证较好的静水压环境,同时测试了极低温(T<100mK)的电阻率ρ(T)和交流磁化率4πχ,如图6所示.
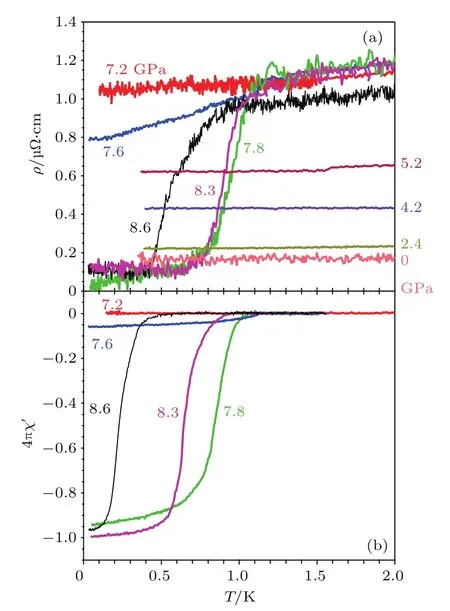
图6 临界压力Pc附近MnP单晶的极低温(a)电阻率ρ(T)和(b)交流磁化率4πχ(T)[17]Fig.6.Temperatu re dependence of(a)the resistivityρ(T)and(b)the ac magnetic susceptibility 4πχ on MnP at lowtemperatures under various pressures near the critical pressure Pc[17]
从图6(a)可以看出,在P=7.6 GPa时,ρ(T)在约1 K开始缓慢下降;当压力升到7.8 GPa时,ρ(T)在约1 K出现陡降,表明可能发生了超导转变;然而当继续增加压力时,此转变往低温移动,这意味着超导转变只存在非常窄的压力区间.遗憾的是,图6(a)所示的ρ(T)并没有达到零电阻,这可能是由于对顶砧式压腔的单轴加压方式和传压介质在低温固化造成高压腔内存在一定的压力不均匀分布,而MnP超导转变存在的压力范围又非常窄造成的.不过,图6(b)所示的交流磁化率数据提供了MnP体超导的直接证据.4πχ(T)在P=7.6 GPa时开始观察到超导抗磁信号,当压力升高到7.8 GPa时超导抗磁体积因子达到了95%,表明进入体超导态;当继续升高压力到8.6 GPa时,超导抗磁体积因子保持不变,但是超导转变温度Tsc降至0.5 K以下.这些结果与图6(a)中的电阻率数据完全符合,进一步证实了观察到的电阻率陡降来源于超导转变,而且超导只存在Pc附近非常窄的压力区间,意味着超导电性的出现与磁性量子临界点具有非常紧密的联系.
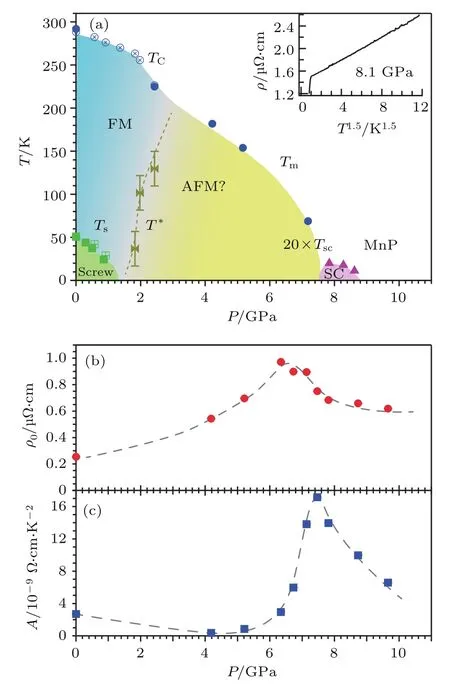
图7 (a)MnP单晶的温度-压强相图,其中给出了磁有序温度TC,Tm,T∗,Ts和超导转变温度Tsc随压力的演化关系,高压首先将铁磁(FM)序压制,然后在3—4 GPa将铁磁序改变为反铁磁序(AFM),最后在Pc≈8 GPa将长程磁有序完全抑制,同时低温出现超导电性(SC);(b),(c)通过对正常态电阻率在低温极限下利用ρ(T)=ρ0+AT2拟合获得的剩余电阻率ρ0和电阻率系数A随压力的变化,它们在Pc附近均表现出显著增强;(a)中插图为P=8.1 GPa的ρ(T)按照ρ-T1.5做图,显示出很好的线性关系[17]Fig.7.(a)Temperatu re-pressure phase diagramof MnP single crystal.Pressure dependences of themagnetic transition temperatures,TC,Tm,T∗,Tsand the superconducting transition temperatu re Tsc;Tschas been scaled by a factor of 20 for clarity.(b),(c)Variation with pressu re of the residual resistivityρ0and the Acoeffi cient ex tracted froma linear fi tting tothe ρ(T2)curves at the low-temperatu re limit.Inset of(a)shows the low-temperatureρ(T)data at 8.1 GPa in the formofρversus T1.5[17].
根据以上数据,我们绘制了MnP单晶的温度-压强相图.如图7(a)所示,外加高压可以逐渐抑制双螺旋反铁磁序(Ts)和铁磁序(TC),前者在约1.4GPa完全消失,后者在2–3GPa转变为新的螺旋反铁磁序(Tm),直到Pc≈8 GPa时完全消失;同时,在Pc附近非常窄(约1GPa)的压力区间观察到Tsc=1 K的超导电性.同样地,MnP的超导相图与CrAs及前面提及的非常规超导体系非常相似,特别是超导存在的压力区间很窄这一点与重费米子超导体,例如CeIn3和CePd2Si2相似[3].不同之处是,MnP的磁有序在高压下表现出更丰富的变化,是目前研究的热点[36−39].
不论MnP在高压下螺旋反铁磁序的具体形式如何,超导电性只出现在Pc附近很窄的压力范围表明反铁磁临界量子涨落与超导配对机理具有重要联系.如图7(a)的插图所示,在Pc附近的正常态电阻率确实表现出ρ(T)∝T1.5的非费米液体行为,与三维反铁磁量子临界点附近准粒子的非相干散射给出的理论值符合[7].此外,根据费米液体理论对低温正常态电阻率进行零温极限的拟合分析,表明电子有效质量m∗/m0在Pc附近表现出非常显著的增强,如图7(b)和图7(c)所示.由于在Pc附近观察到的非费米液体行为和电子有效质量的大幅度提高均是反铁磁量子临界点的典型特征,这些结果均表明MnP中高压诱导的超导电性很可能是反铁磁临界涨落作为配对媒介的非常规机理.同样,电子能带结构计算表明MnP费米面附近的电子态密度主要来源于Mn-3d电子[40],因此MnP成为第一个锰基化合物超导体,这将启发人们去探索更多的锰基非常规超导体.
5 FeSe单晶的高压研究[18]
在铁基高温超导体的母体化合物中,随着温度降低往往会发生四方-正交结构相变,造成旋转对称性的破缺,形成电子向列序,而且在向列序发生的同时或者稍低温度还会出现长程反铁磁序.通过化学掺杂或者施加压力等调控手段将反铁磁序和电子向列序抑制掉会诱导高温超导电性.因此,澄清向列序、磁有序和超导电性的相互关联或竞争关系是理解铁基非常规超导机理的关键[41].
FeSe是铁基超导体系中晶体结构最简单的一员,但是却表现出诸多奇特反常的物理性质,成为近年来的研究焦点.一方面,虽然FeSe在Ts≈90 K也发生四方-正交结构相变[42],但是与其他铁基超导体系截然不同的是,FeSe在向列相内并没有形成长程反铁磁序[43].目前,对FeSe非磁基态的原因以及电子向列序到底是起源于自旋涨落还是轨道序仍存在较大争议[44].另一方面,无需化学掺杂或施加高压,FeSe在正交对称性的向列相内就可以出现Tc≈9 K的超导电性[45].通过对FeSe单晶进行碱金属[46],有机分子或其他离子插层[47]、施加高压[48]、电场调控[49]、或者在SrTiO3衬底上生长单层FeSe薄膜[50]等多种途径,都可以大幅度提高其Tc至30–40 K以上,甚至达到液氮温区[51],从而进入高温超导行列.那么,FeSe是如何从低温超导体转变为高温超导的呢?
通过对FeSe-基高温超导体电子结构的大量研究表明电子掺杂是实现高温超导的关键[49,52].但是,目前已有的基于离子插层和掺杂、电场调控以及单层膜等调控手段得到的实验结果并不能给出高温超导与母体的电子向列序、甚至压力下出现的磁有序之间的具体关系.对FeSe施加高压并没有引入额外的电荷载流子,仍然可以实现近40 K的高温超导[48];而且,高压µSR测试显示[53,54],FeSe在约1 GPa下可以形成长程反铁磁序,并且发现在P<2.5 GPa时磁有序温度Tm与超导转变温度Tc都随压力增加而升高,遗憾的是需要更高的压力才能澄清Tm与Tc的具体关系[55].因此,我们利用活塞-圆筒和立方六面砧高压低温测量装置,详细测试了FeSe单晶高压下的电阻率和交流磁化率,绘制了完整的温度-压力相图,具体阐明了电子向列序、高压诱导的磁有序和超导相之间的相互竞争关系,揭示了高温超导是如何逐步实现的.
图8(a)给出了利用活塞-圆筒压腔测试的0≤P<1.9 GPa范围内的电阻率ρ(T).常压下,ρ(T)在电子向列序转变温度Ts≈90 K出现上翘(箭头所示),然后在Tc=8.5 K实现零电阻超导.随着压力升高,Ts逐渐向低温移动,P>1.5 GPa时降至50 K以下;同时,ρ(T)在Tm≈ 20 K出现另一个上翘,与高压µSR观察到磁有序的温度接近[53,54],并随着压力升高逐步向高温移动.在此压力区间,Tc呈现非单调变化,1.89 GPa时升至约15 K.这些结果与已经报道的高压下的µSR[53,54]、电阻率[55]等实验结果一致.
图8(b)显示的是利用立方六面砧压腔测试的1.8≤P≤8.8 GPa范围内的ρ(T),从中可以清晰地跟踪Tm和Tc随压力完整的演化规律.如图8(b)所示,P=1.8 GPa的ρ(T)数据与活塞-圆筒压腔测试的结果类似,不过电阻率在Tm处的上翘更加显著,这可能是由于六面砧压腔能提供更好的静水压环境.随着压力升高,Tm继续向高温移动,不过电阻率在Tm处的上翘越来越弱,在P≥2.8 GPa时转变为下降的拐点,而且下降的幅度越来越大,不过转变温度逐渐趋近饱和,P=4.8 GPa时达到45 K;在此压力区间,Tc基本保持不变,维持在约20 K附近.然而,当压力从4.8升至5.8 GPa时,ρ(T)表现出较复杂的特征,Tm降至约41 K,表现为电阻率突降之前的拐点(对应dρ/d T曲线上的小峰),Tc跳至约28 K;当P=6.3 GPa时,ρ(T)上只能观察到超导转变,达到38.5 K,然后随着压力升高缓慢降低,8.8 GPa时降至33.2 K.当继续升高压力至约12 GPa时,四方FeSe发生结构相变,从层状结构转变为三维的正交结构(空间群Pbnm).如图8(c)所示,此高压相不超导,ρ(T)表现出半导体型温度依赖关系,且电阻率随着压力的增加而升高.另外,我们还利用日本东京大学的恒压型立方六面砧高压装置对气相传输法生长的FeSe单晶开展了高压电阻率测试,得到非常一致的结果,如图8(d)所示.

图8 FeSe单晶高压下的电阻率ρ(T) (a)采用活塞-圆筒压腔测试到1.9 GPa;(b),(c)采用中国科学院物理研究所的微型立方六面砧压腔测试到15 GPa;(d)采用日本东京大学的恒压型立方六面砧压腔测试到8 GPa;不同颜色的箭头对应Ts,Tm和Tc[18]Fig.8.Temperature dependence of resistivity ρ(T)in FeSe single crystals under high pressure:(a)ρ(T)cu rves below100 Kat d iff erent pressures upto1.9 GPa measured in the self-clamped piston-cy linder cell;(b),(c)data upto8.8 GPa and 15 GPa measu red in the self-clamped cubic anvil cell in IOP CAS;(d)ρ(T)curves below200 Kupto8 GPa measured in the constant-loading cubic anvil cell in ISSP,Univ.Tokyo.Except for(c)the data are vertically shifted for clarity.The resistive anomalies at transition temperatures Ts,Tm,and Tcare ind icated by the arrows[18].
为了进一步证实图8(b)中电阻率的上翘或下降对应于反铁磁序,特别是2.8≤P≤4.8 GPa之间电阻率的下降不是超导相变的起始点,我们还在每个压力下测试了不同磁场的ρ(T),如图9所示.从P=1.8 GPa的ρ(T)曲线可以看出,随着磁场的增加,Tm是不变的,而Tc逐渐向低温移动.当P=2.8 GPa时,随着磁场的增加,零场时Tm处的电阻率下降逐渐变为上翘,而且Tm随磁场不变,证实零场时观察到的电阻率反常对应的是反铁磁序而非超导转变的起始.从P=5.8 GPa时不同磁场下的ρ(T)曲线上,我们也进一步确认电阻率在约38 K的突降对应于部分样品的超导转变,Tm对应于电阻突降之前的拐点,如图9(d)中箭头所示.通过施加磁场压低Tc,我们在P=6.3GPa,H=9 T的ρ(T)曲线也可以看到反铁磁序的特征,图9(i)中箭头所示,表明反铁磁序已降至超导转变以下.此外,我们还测试了高压下的交流磁化率,超导抗磁信号出现的温度与达到零电阻的温度Tc非常一致[18].
根据上述测试结果,我们绘制了FeSe单晶目前最完整温度-压力相图.如图10所示,随着压力升高,电子向列序温度Ts逐渐降低,1.5 GPa时降到50 K以下,同时在Tm≈20 K开始出现长程磁有序,这表明向列序和反铁磁序之间存在竞争关系.随着压力的继续增加,Ts外推至2 GPa时将完全消失,而Tm则逐渐升高,在约4.5 GPa时到达最高的45 K,之后又逐渐降低,呈现出圆顶状Tm(P),其两端分别外推至1 GPa和8 GPa附近.伴随着压力下电子向列序的消失和磁有序的出现,超导转变温度Tc表现出一系列相应的特征变化:随着Ts的降低Tc首先升高,在约1 GPa附近达到一个局域极大值,然后逐渐降低,这对应于Tm开始出现的下临界压力,意味着磁有序会抑制超导;当Ts在2 GPa完全消失时,Tc出现第一次台阶式跳跃,升至约20 K,表明电子向列序和超导之间也存在竞争关系;在Tm保持升高的2–5 GPa压力区间,Tc几乎保持不变,进一步表明反铁磁序和超导之间存在竞争关系;当压力升高到约6 GPa时,Tm开始降低,同时Tc出现第二次台阶式跳跃,实现最高的超导转变;之后,Tc随着压力的增加而缓慢降低;最终,在约12 GPa时层状FeSe发生结构相变,转变为具有三维晶体结构的非超导的六角FeSe.
图10给出的温度-压力相图详细展示了FeSe单晶中电子向列序、磁有序和超导相之间的相互竞争关系,具体揭示了FeSe单晶中的高温超导是通过依次抑制电子向列序和反铁磁序而逐步实现的.特别是,高温超导近邻长程磁有序与其他铁基超导体系类似,而且磁有序消失的临界压力附近的正常态电阻率表现出很好的线性温度依赖关系,见图8(b),表明临界反铁磁涨落可能对实现高温超导起重要作用.值得注意的是,FeSe中磁有序温度Tm和最高超导Tc非常接近,意味着磁有序和超导配对之间具有非常相近的能量尺度,这与其他铁基超导体系是不同的.
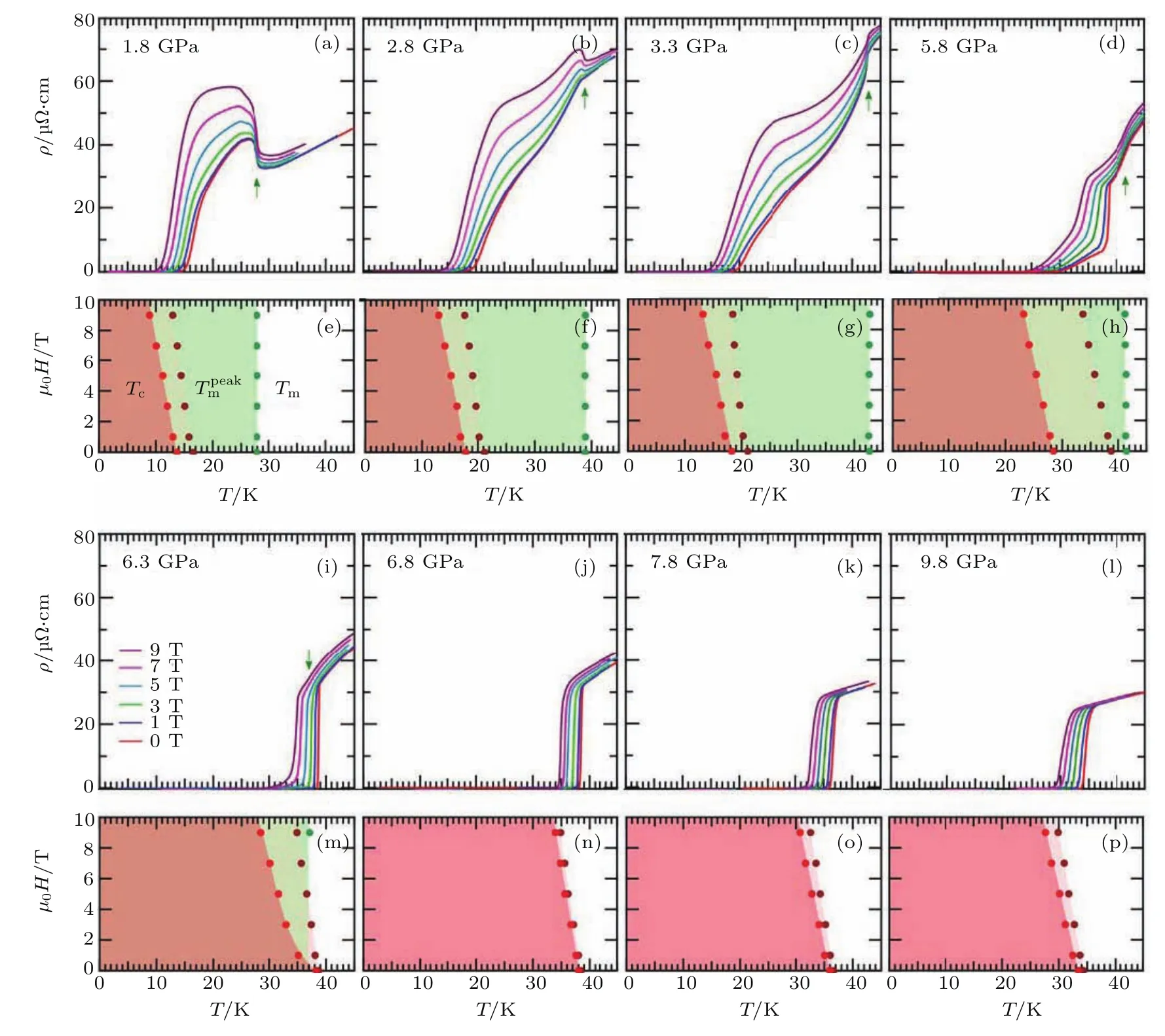
图9 FeSe单晶在高压和不同磁场下的低温ρ(T)数据((a)—(d),(i)—(l))和相应的H-T相图((e)—(h),(m)—(p)),从图中可以看出随着磁场增加,磁有序温度Tm保持不变,而超导转变温度Tc逐渐降低[18]Fig.9.E ff ects of magnetic fields on the magnetic and superconducting transitions under diff erent high pressu res.The magnetic transition temperatu re Tmis field independent and marked by the green arrow(a)–(d)[18].
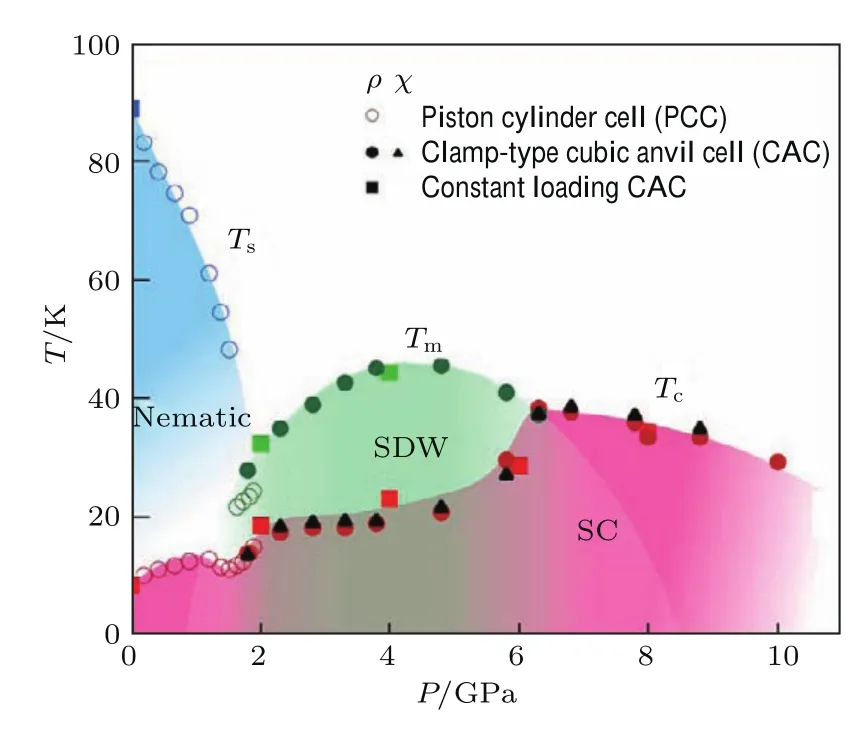
图10 FeSe单晶的温度-压力相图,其中Ts,Tm,Tc分别代表电子向列序(nematic)、长程磁有序(SDW)和超导(SC)转变温度[18]Fig.10.Temperatu re–pressure phase diagramof bu lk FeSe,in which Ts,Tm,and Tcrepresent the transition temperatures for nematic order,long-range antiferromagnetic order and the superconductivity[18].
6 结论与展望
高压调控是实现磁性量子临界点、探索非常规超导电性非常有效的研究手段.为了能够在较大的压力范围开展高压研究,我们在中国科学院物理研究所建立了国内第一台基于立方六面砧的大腔体高压低温物性测量装置,实现了多重极端条件(最高压强15 GPa,最低温度1.4 K和最强磁场9 T)下的电输运和磁性测试,其三轴加压和样品浸泡在液体传压介质中的方式能保证良好的静水压环境,有利于获得材料本征的高压效应.此外,由于样品空间相对较大,开发更多能够与立方六面砧高压装置配合使用的物性测量技术,例如10 GPa以上的高压核磁共振测量,是将来应着重发展的高压技术方向.
借助于能提供较好静水压环境的立方六面砧和活塞-圆筒高压低温物性测量装置,我们首先对具有双螺旋反铁磁序的巡游电子磁体CrAs和MnP开展了详细的高压物性调控研究,分别在Pc≈0.8 GPa和8.0 GPa抑制了它们的长程磁有序,并在Pc附近观察到ρ∝T1.5的非费米液体行为和电子有效质量的显著提高,这些现象是反铁磁量子临界点的典型特征.最重要的是,我们还在Pc附近首次观察到Tc=2 K(CrAs)和1 K(MnP)的超导电性,相继实现了铬基和锰基化合物超导体零的突破.这两个发现打破了人们认为铬基和锰基化合物不会出现超导这一普遍认识,从而启发人们探索新型的铬基和锰基非常规超导体.新型准一维超导体系A2Cr3As3(A=K,Rb,Cs)的发现也表明这一研究领域是很有潜力的.此外,这两个工作也进一步印证了通过高压实现磁性量子临界点确实是探索非常规超导体非常有效的手段.因此,非常有必要对更多的巡游电子磁体开展系统深入的高压调控研究,我们可以预期将会发现更多的有趣的物理现象.
此外,对FeSe单晶的高压研究表明,高压还可以大幅度提高非常规超导体的Tc,揭示多种电子序之间的相互竞争关系.通过绘制FeSe单晶完整的温度-压力相图,具体阐明了电子向列序、磁有序和超导相之间的相互竞争关系,并揭示了FeSe单晶中的高Tc是通过依次抑制电子向列序和磁有序而逐步实现的.特别是FeSe的最高Tc出现在反铁磁序消失的临界压力附近,且正常态电阻率呈现线性温度依赖关系,表明临界反铁磁涨落与其高温超导具有重要关联.这些现象与其他FeAs基高温超导体系类似,有助于统一理解FeSe-和FeAs-基高温超导的机理.
本文中的工作是作者在过去三年中与多位合作者共同完成的.感谢中国科学院物理研究所雒建林研究员和吴伟提出对CrAs进行高压研究并提供了高质量的CrAs和MnP单晶样品;感谢中国科学院物理研究所的孙建平和叶光洲同学开展的大量高压低温物性测量工作,特别是孙建平同学在搭建立方六面砧装置过程中付出了大量努力.感谢日本东京大学的Uwatoko教授在搭建立方六面砧高压测量装置方面给予的大力帮助、Matsubayashi博士在利用对顶砧压腔和稀释制冷机测量MnP极低温物性方面的帮助、以及Matsuura和Shibauchi教授在利用恒压型六面砧压腔测量气相传输FeSe单晶方面的合作.感谢美国橡树岭国家实验室的闫加强博士和Sales博士提供了高质量的FeSe单晶样品.最后,感谢中国科学院物理研究所和中组部“青年千人计划”在搭建高压实验室时给予的经费支持.
[1]Coleman P,Schofield AJ 2005Nature433 226
[2]Sachdev S,Keimer B2011Phys.Today64 29
[3]Mathur N D,G rosche F M,Julian SR,W alker IR,Freye D M,Haselwimmer R KW,Lonzarich G G 1998Nature394 39
[4]Norman MR 2011Science332 196
[5]Monthoux P,Pines D,Lonzarich G G 2007Nature450 1177
[6]Gegenwart P,Si Q,Steglich F 2008Nat.Phys.4 186
[7]Lohneysen HV,Rosch A,Vojta M,Wölfl e P 2007Rev.Mod.Phys.79 1015
[8]Yu W,Aczel AA,W illiams TJ,Bud’koS L,Ni N,Can field P C,Luke G M2009Phys.Rev.B79 020511
[9]Matsubayashi K,Terai T,Zhou J S,UwatokoY 2014Rhys.Rev.B90 125126
[10]W ang BS,Matsubayashi K,Cheng J G,Terashima T,Kihou K,Ishida S,Lee C H,IyoA,Eisaki H,UwatokoY 2016Phys.Rev.B94 020502
[11]UwatokoY 2002Rev.High Pressure Sci.Technol.12 306
[12]Mori N,Takahashi H,Takeshita N 2004High Pressure Res.24 225
[13]Cheng J G,Matsubayashi K,Nagasaki S,Hisada A,Hirayama T,HedoM,Kagi H,UwatokoY 2014Rev.Sci.Instrum.85 093907
[14]MaoHK,Bell P M1981Rev.Sci.Instrum.52 615
[15]Rotundu C R,Cuk T,G reene R L,Shen Z X,Hemley R J,Struzhkin V V 2013Rev.Sci.Instrum.84 063903
[16]W u W,Cheng J G,Matsubayashi K,Kong P P,Lin F K,Jin C Q,W ang N L,UwatokoY,LuoJ L 2014Nat.Commun.5 5508
[17]Cheng J G,Matsubayashi K,W u W,Sun J P,Lin F K,LuoJ L,UwatokoY 2015Phys.Rev.Lett.114 117001
[18]Sun J P,Matsuu ra K,Ye G Z,Mizukami Y,Shimozawa M,Matsubayashi K,Yamashita M,W atashige T,Kasahara S,Matsuda Y,Yan J Q,Sales BC,UwatokoY,Cheng J G,Shibauchi T2016Nat.Commun.7 12146
[19]Mori N,Takahashi H,Miyane Y 1990Kotai Butsuri25 185
[20]UwatokoY,Matsubayashi K,AsoN,NishiM,Fu jiwara T,HedoM,Tabata S,Takagi K,TadoM,Kagi H2008Rev.High Pressure Sci.Technol.18 230
[21]Matsubayashi K,Hisada A,Kawae T,UwatokoY 2012Rev.High Pressure Sci.Technol.22 206
[22]Boller H,Kallel A1971Solid State Commun.9 1699
[23]Selte K,Kjekshus A,Jamison W E,And resen A,Engeb retsen J E 1971Acta Chem.Scand.25 1703
[24]W atanabe H,Kazama N,Yamaguichi Y,OhashiM1969J.Appl.Phys.40 1128
[25]W u W,Zhang X D,Y in Z H,Zheng P,W ang N L,LuoJ L 2010Sci.China:Phys.Mech.Astron.53 1207
[26]Zavadskii E A,Sibarova IA1980Sov.Phys.JETP51 542
[27]Kotegawa H,Nakahara S,Akamatsu R,Tou H,Sugawara H,Harima H2015Phys.Rev.Lett.114 117002
[28]ItoT,IdoH,Motizuki K2007J.Magn.Magn.Mater.310 558
[29]BaoJ K,Liu J Y,Ma C W,Meng Z H,Tang Z T,Sun Y L,Zhai HF,Jiang H,BaiH,Feng C M,Xu Z A,CaoG H2015Phys.Rev.X5 011013
[30]Tang Z T,BaoJ K,Liu Y,Sun Y L,Ab limit A,Zhai HF,Jiang H,Feng C M,Xu Z A,CaoG H2015Phys.Rev.B91 020506
[31]Tang Z T,BaoJ K,W ang Z,Bai H,Jiang H,Liu Y,Zhai HF,Feng C M,Xu Z A,CaoG H2015Sci.China:Mater.58 16
[32]Huber E E J,Ridgley HD 1964Phys.Rev.135 A1033
[33]Felcher G P 1966J.Appl.Phys.37 1056
[34]Takase A,Kasuya T1980J.Phys.Soc.Jpn.48 430
[35]Banus MD 1972J.Solid State Chem.4 391
[36]Matsuda M,Ye F,Dissanayake S E,Cheng J G,Chi S,Ma J,Zhou HD,Yan J Q,Kasamatsu S,SuginoO,KatoT,Matsubayashi K,Okada T,UwatokoY 2016Phys.Rev.B93 100405
[37]Fan G Z,ZhaoB,W u W,Zheng P,LuoJ L 2016Sci.China:Phys.Mech.Astron.59 657403
[38]Khasanov R,AmatoA,Bon fa P,Guguchia Z,Luetkens H,Morenzoni E,de Renzi R,Zhigad loN D 2016Phys.Rev.B93 180509
[39]W ang Y S,Feng Y J,Cheng J G,W u W,LuoJ L,RosenbaumTF 2016Nat.Commun.7 13037
[40]Yanase A,Hasegawa A1980J.Phys.C13 1989
[41]Davis J C,Lee D H2013Proc.Natl.Acad.Sci.USA110 17623
[42]McQueen TM,W illiams AJ,Stephens PW,TaoJ,Zhu Y,Ksenofontov V,Casper F,Felser C,Cava R J 2009Phys.Rev.Lett.103 057002
[43]Imai T,Ahilan K,N ing F L,McQueen TM,Cava R J 2009Phys.Rev.Lett.102 177005
[44]G lasb renner J K,Mazin II,Jeschke HO,Hirsch feld P J,Fernandes R M,Valenti R 2015Nat.Phys.11 953
[45]Hsu F C,LuoJ Y,Yeh KW,Chen TK,Huang TW,W u P M,Lee Y C,Huang Y L,Chu Y Y,Yan D C,Wu MK2008Proc.Natl.Acad.Sci.USA105 14262
[46]GuoJ G,Jin S F,W ang G,W ang S C,Zhu KX,Zhou TT,He M,Chen X L 2010Phys.Rev.B82 180520
[47]Burrard-Lucas M,Free D G,Sed lmaier S J,W right JD,Cassidy S J,Hara Y,Corkett AJ,Lancaster T,Baker P J,Blundell S J,C larke S J 2012Nat.Mater.12 15
[48]Medvedev S,McQueen TM,Troyan IA,Palasyuk T,Eremets MI,Cava R J,Naghavi S,Casper F,Ksenofontov V,W ortmann G,Felser C 2009Nat.Mater.8 630
[49]Lei B,Cui J H,X iang Z J,Shang C,Wang N Z,Ye G J,LuoX G,W u T,Sun Z,Chen X H2016Phys.Rev.Lett.116 077002
[50]W ang Q Y,Li Z,Zhang W H,Zhang Z C,Zhang J S,Li W,Ding H,Ou Y B,Deng P,Chang K,Wen J,Song C L,He K,Jia J F,Ji S H,W ang Y Y,W ang L L,Chen X,Ma X C,Xue Q K2012Chin.Phys.Lett.29 037402
[51]Ge J F,Liu Z L,Liu C H,GaoC L,Q ian D,Xue Q K,Liu Y,Jia J F 2014Nat.Mater.14 285
[52]Liu X,ZhaoL,He S L,He J F,Liu D F,Mou D X,Shen B,Hu Y,Huang J W,Zhou X J 2015J.Phys.:Condens.Mater.27 183201
[53]Bendele M,AmatoA,Conder K,E lender M,Keller H,Klauss HH,Luetkens H,Pomjakushina E,Raselli A,Khasanov R 2010Phys.Rev.Lett.104 087003
[54]BendeleM,IchsanowA,Pashkeich Yu,Keller L,Strassle T,Gusev A,Pomjakushina E,Conder K,Khasanov R,Keller H2012Phys.Rev.B85 064517
[55]TerashiamT,Kikugawa N,Kasahara S,W atashige T,Shibauchi T,Matsuda Y,W olf T,Bohmer AE,Hardy F,Meingast C,Lohneysen HV,Uji S 2015J.Phys.Soc.Jpn.84 063701
PACS:74.40.Kb,74.25.Dw,74.62.Fj,74.70.XaDOI:10.7498/aps.66.037401
P ressu re-tuned magnetic quantumcritical point and unconventional superconductiv ity∗
Cheng Jin-Guang†
(Key Laboratory of Ex treme Cond itions Physcis,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China)(Received 2 November 2016;revised manuscript received 19 November 2016)
Magnetic quantumcritical point(QCP)arises when a long-rangemagnetic order occurring at finite temperature can be suppressed toabsolute zerotemperature by using chemical substitutions or exerting high pressure.Exotic phenomena such as the non-Fermi-liquid behaviors or the unconventional superconductivity are frequently observed near themagnetic QCP.In comparison with chemical substitutions,the application of high pressure has some advantages in the sense that it introduces nochemical disorder and can approach the QCP in a very precisemanner.In this article,our recent progress in exploring the unconventional superconductors in the vicinity of pressure-induced magnetic QCP is reviewed.By utilizing the piston-cy linder and cubic-anvil-cell apparatus that can maintain a relatively good hyd rostatic pressure condition,we fi rst investigated systematically the eff ect of pressure on the electrical transport properties of the helimagnetic CrAs and MnP.We discovered for the fi rst time the emergence of superconductivity belowTc=2 Kand 1 Knear their pressure-induced magnetic QCPs at Pc≈0.8GPa and 8 GPa for CrAs and MnP,respectively.They represent the fi rst superconductor among the Cr-and Mn-based compounds,and thus open a newavenue tosearching novel superconductors in the Cr-and Mn-based systems.Then,we constructed themost comprehensive temperature-pressure phase diagramof FeSe single crystal based on detailed measurements of high-pressure resistivity and alternating current magnetic susceptibility.We uncovered a dome-shaped magnetic phase superseding the nematic order,and observed the sudden enhancement of superconductivity withKaccompanied with the suppression ofmagnetic order.Our resu lts revealed explicitly the competing nature of nematic order,antiferromagnetic order,and superconductivity,and howthe high-Tcsuperconductivity is achieved by suppressing the long-range antiferromagnetic order,suggesting the important role of antiferromagnetic spin fluctuations for the Cooper paring.These aforementioned results demonstrated that high pressure is an eff ective approach toexploring or investigating the anomalous phenomena of strongly correlated electronic systems by finely tuning the competing electronic orders.
high-pressuremeasurements,magnetic quantumcritical point,unconventional superconductivity,non-Fermi-liquid behaviors
10.7498/aps.66.037401
∗国家自然科学基金(批准号:11574377)、国家重点基础研究发展计划(批准号:2014CB921500)和中国科学院先导B项目(批准号:XDB07020100)资助的课题.
†通信作者.E-mail:jgcheng@iphy.ac.cn
*Project supported by the National Natu ral Science Foundation of China(G rant No.11574377),the National Basic Research Programof China(G rant No.2014CB921500),and the Strategic Priority Research Program(B)of the Chinese Academy of Sciences(G rant No.XDB07020100).
†Corresponding author.E-mail:jgcheng@iphy.ac.cn
